基于最小偏差的大型转子绕线直线插补算法

陈小勇，黄靖,2，李建兴,2，林龙彬，罗堪,2

(1.福建工程学院 信息科学与工程学院，福建 福州 350118；2.福建省数字化装备重点实验室，福建 福州 350118)

基于最小偏差的大型转子绕线直线插补算法

陈小勇1，黄靖1,2，李建兴1,2，林龙彬1，罗堪1,2

(1.福建工程学院 信息科学与工程学院，福建 福州 350118；2.福建省数字化装备重点实验室，福建 福州 350118)

分析了大型转子绕线机的运动模型,采用最小偏差准则，给出了实现绕线机飞叉轴和水平轴运动控制的直线插补算法。并进一步通过仿真和实际绕线实验验证该算法的有效性。在仿真实验中，采用的最小偏差直线插补算法具有较好的绕线精度；在RW400大型绕线机实际绕线测试实验中，大型电机转子绕线间距均匀，排列紧密，单圈误差小于0.1%。实验结果表明，最小偏差直线插补算法能够较好地用于大型电机转子绕线机插补运动控制。

绕线机； 插补算法； 最小偏差； 运动控制

随着工业自动化进程的不断推进，高性能电机的供需矛盾日益突出。电机性能与转子漆包线绕线精度密切相关[1]。因此，实现高精度电机转子绕线成为高性能电机生产迫切需要解决的关键技术问题。传统的绕线机旋转主轴多采用力矩电机驱动，排线机构与主轴通过机械齿耦合连接[2]。力矩电机开环控制和纯机械耦合使得传统绕线机采用分步绕线，轴间联动性差，同时存在机械磨损大、噪声大、排线精度低等缺点。随着计算机辅助加工技术的不断进步，采用数控设备作为控制系统的绕线机逐渐成为主流[3]。新型数控系统通过插补算法控制机械轴运动逼近理想绕线运动模型[4]。目前在绕线机中常用的插补算法包括了逐点比较法、数字积分法、改进数字积分法[5]等。使用逐点比较法和积分形式的数控系统在实际绕线过程中存在绕线误差大[6]，控制轴运动效率低等问题[7]。改进数字积分插补算法能够使绕线误差小于0.5个脉冲[5]。然而对于两轴运动轨迹相互正交且轴运动距离比例较大的场合(如绕线机机床)，运用文献所提到的改进数字积分算法效果并不理想。针对绕线机高精度绕线轴间联动控制问题，本文分析了旋转轴和水平进给轴间运动模型，在遵循最小偏差[6]准则和轴间联动前提下，设计了用于相互正交轴上电机运动控制的直线插补算法。该算法通过最小化运动轨迹与理论轨迹间的误差确定各轴控制脉冲指令。为了验证最小偏差直线插补算法的有效性，论文对所提出的算法进行仿真并与改进数字积分型[6]插补算法进行对比，最后将算法在RW400大型自动转子绕线机上进行了实际绕线测试。

1 自动绕线机运动模型分析

1.1 自动绕线机机械结构

典型的大型绕线机机械结构示意图如图1所示。主要包括了：转子固定装置、张力装置、水平进给平台、圆盘、飞叉、控制进给平台和圆盘旋转的伺服电机以及极轴电机等。待绕线的转子通过转子固定装置固定在水平进给平台上；张力装置通过气动方式将待绕制的漆包线绷紧；进给平台伺服电机和圆盘旋转伺服电机分别通过传动装置控制进给平台和飞叉做水平运动和旋转运动；极轴电机控制转子绕转子中心轴每次90度转动，用于实现电机转子各极的依次绕线。

图1 绕线机机械结构示意图Fig.1 Typical mechanical schematic of wire machine

1.2 绕线运动模型分析

电机转子绕线包括了两个相互正交轴的运动：(1)固定飞叉的圆盘做旋转运动；(2)固定电机转子平台做水平进给运动。理想的轴间联动，即飞叉旋转一周，平台进给一个漆包线的线径，可保证高精度的绕线。针对绕线运动过程建立绕线运动模型如图2所示。以圆盘中心C1为原点建立空间直角坐标系如图2(a)所示，设O1为飞叉运动的起点，O1C1的距离为r，待绕制的漆包线线径为d，绕线电机做匀速运动，通过传动装置带动平台和飞叉的运动速度分别为vx和vy。两轴联动绕线时，转子单圈绕线将满足公式(1)：

其中x和y分别代表进给距离和飞叉运动弧长。

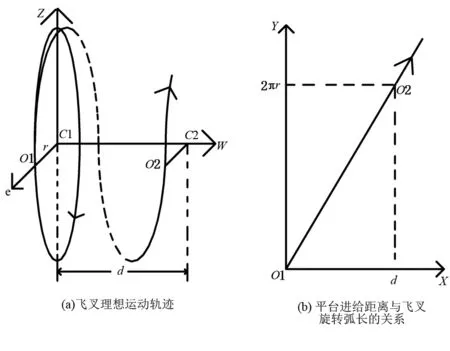
图2 绕线运动模型Fig.2 Motion model of wire winding

将飞叉运动轨迹投影到分别以进给距离和飞叉运动弧长为横、纵坐标的直角坐标系中。通过图2(b)的模型映射关系，可将飞叉在空间中的螺旋轨迹映射为建立距离直角坐标系中的直线。如能够保证电机严格沿图2(b)O1O2方向运动，则机器将能够实现完美绕线。因此，绕线机中精密绕线控制的实质是保证运动飞叉旋转弧长与平台进给距离成线性。

2 基于最小偏差准则的直线插补算法

2.1 最小偏差插补原理

偏差是精度评估最常用的测度之一。为了实现精准绕线，采用最小偏差原则对绕线运动模型分析。在平台进给距离与飞叉旋转弧长分别为横纵坐标的直角坐标系中(图 3)，设理想的运动轨迹为N=[n1,n2,...,ni]，实际运动轨迹为M=[m1,m2,...,mj]，最小偏差要保证误差绝对值之和最小min{‖N-M‖}。

图3 最小偏差原理Fig.3 The diagram of least error principle

坐标系中的直线OE为理想的绕线轨迹，轨迹上的任意点N(xI,yI)满足公式(2)，k为比例因子，N点在横坐标上的投影为D。

而实际绕线轨迹受机械结构以及伺服电机寄存器等诸多因素影响[8]，往往不能够准确的落在直线ON上。设实际绕线位置为M(xR,yR)，则偏差函数定义为：

设P为理想轨迹上的一点，且MP平行于ND。P点坐标满足公式(4)，可将FM改写为：

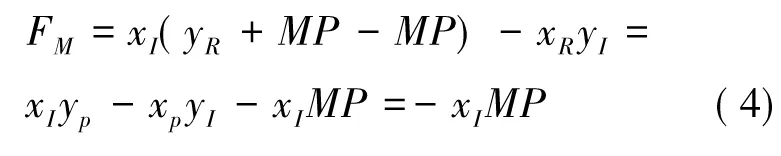
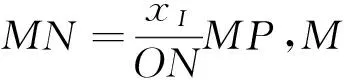
由公式(5)可知插补偏差正比于偏差函数FM。

实际系统在固定时刻只能向x，y方向或同时向x和y方向进给。设终点坐标为E(xE,yE)，x和y轴伺服电机单位脉冲步进距离分别为lx和ly，则对应电机脉冲计数为[9]：

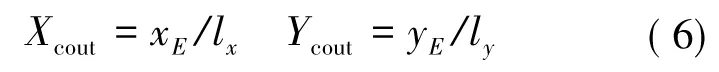
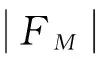
2.2 最小偏差插补算法

通过以上分析，根据最小偏差插补原理，绕线机插补算法具体实现步骤如下：

(1)比较公式(6)中的两个脉冲计数值，向计数大的方向持续发送脉冲。

(3)判断已走脉冲数是否等于总脉冲数。已走脉冲数小于总脉冲数时转步骤(2)，否则结束绕线。

3 实验结果

为了验证设计的绕线机插补算法的有效性，本文设计了仿真和实际绕线实验。在仿真实验中，论文对比了本文提出的方法和改进数字积分式插补算法[5]的绕线误差，根据RW400型绕线机设置实验参数如下：飞叉半径设为500 mm，电机寄存器设为210，对所需线径为2.50mm型号为LSA423的转子进行绕制；实际绕线测试为采用移植了本文算法基于NUMPower1040数控系统[10-11]的RW400大型绕线机对LSA423型号转子进行1圈8次独立绕线测试，并通过系统光栅位置传感器读取的信号分析绕线误差。

3.1 仿真结果

论文采用公式(7)中的平均欧式距离来评价绕线误差，

仿真实验结果如图 4所示，改进数字积分插补和最小偏差直线插补算法的误差分别为2.849μm和2.199μm。改进数字积分型插补算法产生的平均误差是本文算法的1.29倍。在绕线机这一类轴间运动距离差较大的场合，最小偏差直线插补优于积分型插补算法。

3.2 实际结果

实际绕线测试误差结果和绕线效果分别如表1图5所示。8次绕线误差均值为2.51μm，标准差为0.048 μm。考虑到漆包线线径为2.5mm，设计的控制系统单圈绕线误差小于0.1%。从实际绕线效果(图5b)可以看到，绕制完成后的转子上漆包线线距分布均匀，排列紧密，达到了大型电机转子绕线的要求。实验结果进一步证明了本文采用的最小偏差直线插补算法能够保证绕线机实现高精度绕线作业。

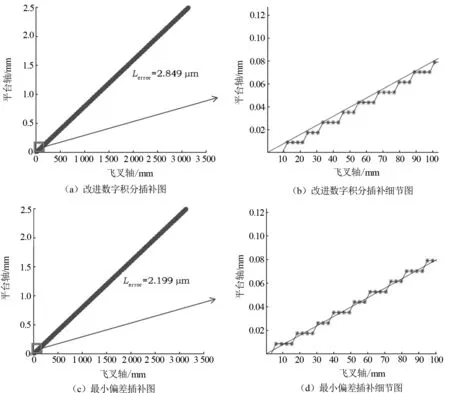
图4 两种插补仿真结果图Fig.4 The simulation results of two kinds of interpolation

表1 实际绕线测试结果(2.5 mm漆包线，1圈，8次)Tab.1 Results of practical winding test (wire diameter: 2.5 mm, 1 circle, 8 times)

图5 实际绕线测试图Fig.5 The actual winding test

4 总结

本文提出采用最小偏差直线插补算法实现转子绕线机两轴联动控制。并通过仿真对比两种插补算法，提出的方法具有较小的绕线误差；将最小偏差直线插补算法运用在RW400大型绕线机上进行实际绕线测试,结果表明所提出算法的绕线机绕制的转子排线间距均匀，排列紧密，单圈误差小于0.1%。最小偏差直线插补算法能较好地应用于大型电机转子绕线机上，具有较高的绕线精度。

[1]王艳新,赵春锋.基于PLC的双飞叉绕线机控制系统设计[J].组合机床与自动化加工技术,2009(7):72-74.

[2]惠晶.绕线机步进驱动自动控制系统[J].电气传动,2005,35(8):56-59.

[3]Shi Yaoyao, Tang Hong, Yu Qiang. Development of NC tape winding machine[M]. London: Springer,2008:753-762.

[4]刘洪玮,郭吉丰,孙云云,等. 两轴伺服控制的绕线机系统[J].电气传动,2010,40(9):9-12.

[5]郭永环,范希营,刘凤国.一种新型的数字积分直线插补算法的研究[J].制造技术与机床,2012(4):164-167.

[6]李腾飞,凌有铸,刘敬猛.基于最小偏差法插补技术的FPGA设计与实现[J].重庆理工大学学报(自然科学版),2013,27(5):90-93.

[7]伍晓亮,田怀文,江晓亮,等.精密电阻绕线机送丝机构的设计与改进[J].现代制造工程,2016(1):105-109.

[8]Kiyoshi O，Yasuaki O，Hideo D.A speed control method for a pm motor using a speed observer and a low-resolution encoder[J].Electrical Engineering in Japan,2003,143(143):66-75.

[9]惠晶,王伟.两轴同步协调控制的绕线机系统[J].机床与液压,2013(13):71-74.

[10]叶春林,刘佳. NUM数控系统参数的调整与应用[J]. 设备管理与维修,2015(S2):288-291.

[11]陈劲松. NUM数控系统的使用与维修(第7讲 NUM数控系统的软件及通信)[J]. 机械工人(冷加工),2003(7):77-78.

(特约编辑：黄家瑜)

Algorithm of large sized (scale)rotor winding machine based on minimum deviation interpolation

Chen Xiaoyong1, Huang Jing1,2, Li Jianxing1,2, Lin Longbin1, Luo Kan1,2

(1.College of Information Science and Engineering, Fujian University of Technology, Fuzhou 350118, China;2.Fujian Provincial Key Laboratory of Digital Equipment, Fuzhou 350118, China)

Motion models of large sized rotor winding machine were analysed. A linear interpolation algorithm for implementing the motion control of wiring fork rotation axis and platform horizontal axis (movement) via the least error principle were presented. The effectiveness of the algorithm was verified with simulation and practical wiring experiments. The simulation results show that the proposed least error linear interpolation algorithm has favourable wiring accuracy (good performance). In the practical RW400 large machine wiring (winding) test, the wires are uniformly and compactly arrayed in the test motor rotor with a percentage of error being under 0.1% in one circle wiring. The results indicate that the proposed method can be well used in the interpolation motion control of large sized rotor windng machine.

winding machine; interpolation algorithm; least error; motion control

2016-11-25

福建省教育厅科技项目(JA13228)

陈小勇(1992-)，男，福建福安人，硕士研究生，研究方向为电气控制工程。

10.3969/j.issn.1672-4348.2016.06.011

TP273

A

1672-4348(2016)06-0567-05