基于申威1600的3级BLAS GEMM函数优化①
2016-02-20刘芳芳蒋丽娟中国科学院软件研究所北京0090中国科学院大学北京0090
刘 昊, 刘芳芳, 张 鹏, 杨 超, 蒋丽娟(中国科学院 软件研究所, 北京 0090)(中国科学院大学, 北京 0090)
基于申威1600的3级BLAS GEMM函数优化①
刘 昊1,2, 刘芳芳1, 张 鹏1,2, 杨 超1, 蒋丽娟1,21(中国科学院 软件研究所, 北京 100190)2(中国科学院大学, 北京 100190)
BLAS是当前科学计算领域重要的底层支持数学库之一, 其中的3级BLAS函数应用最为广泛. 本文基于国产申威1600平台, 提出了一种基础线性代数库BLAS的三级函数通用矩阵乘GEMM的高性能实现方法. 在单核上, 使用乘加指令、循环展开、软件流水线指令重排、SIMD向量化运算、寄存器分块技术等与平台架构相关的技术手段, 实现汇编级手工优化; 在多核上, 提出了适用于该平台的多线程加速方案. 实验结果显示, 在单核串行性能测试中, 与知名开源数学库GotoBLAS相比, 我们实现了平均4.72倍的加速效果; 在多核并行扩展测试中, 4线程版的性能则平均达到了单线程版性能的3.02倍.
申威1600; 三级BLAS; GEMM; 高性能计算; 多核
1 引言
1.1 背景介绍
BLAS(Basic Linear Algebra Subprograms)是一个线性代数核心子程序的集合,主要包括向量和矩阵的基本操作. 它是最基本和最重要的数学库之一, 广泛应用于科学工程计算. 目前世界上有关矩阵运算的软件几乎都调用BLAS数学库; 重要的稠密线性代数算法软件包(如EISPACK、LINPACK、LAPACK和ScaLAPACK等)的底层都是以BLAS为支撑. BLAS目前已成为线性代数领域的一个标准API库.
BLAS分成三个等级:
1级: 进行向量-向量操作;
2级: 进行向量-矩阵操作;
3级: 进行矩阵-矩阵操作.
本文主要研究BLAS 3级中的通用矩阵相乘GEMM函数, 如公式(1)所示, 其中A, B, C表示矩阵,α,β为标量因子.

针对特定的体系结构进行BLAS库的优化, 特别是GEMM函数的优化工作, 国内外已有相当多的研究成果, 例如Goto等人所提出的矩阵乘法实现算法, 通过对矩阵A和B进行划分, 矩阵乘法细分为一组panel-panel的乘法操作(GEBP), 分析矩阵计算三重循环顺序与cache缓存之间的关系模型并提出最优算法[1][2]. 基于该模型的开源高性能BLAS数学库有Texas大学超级计算中心高性能计算组开发的GotoBLAS[3].近几年来, 针对BLAS的自动调优技术日渐成熟, ATLAS数学库可以针对通用CPU平台进行自动调优,通过自动调整矩阵分块、监测cache利用率、调整寄存器使用策略等方式, 生成最合适平台架构的代码[4].
近年来随着CPU+GPU异构并行计算的兴起, 基础线性代数库在这些异构平台上的高性能实现也出现大量优秀科研成果[5,6]. 与本文所述的基于稠密矩阵的BLAS优化工作不同, 很多基于STENCIL计算而出现的稀疏矩阵若以稠密方式进行计算则明显效率低下,面向这些稀疏矩阵实现高性能的BLAS库是近年来该领域的另一个重要方向[7].
神威蓝光国产超级计算机是由国家并行计算机工程研究中心开发研制的首台全部采用国产CPU构建的千万亿次超级计算机系统, 处理器采用自主设计生产的申威1600 CPU, 于2011年10月份在国家超级计算济南中心投入使用, 其布局按照MPP万万亿次架构设计, 主频975MHz-1.1GHz, 单CPU 16核心[8], CPU总数为8704, CPU核心总数接近14万, 峰值计算速度达到每秒1100万亿次浮点计算, 持续计算能力为738万亿次.
随着高性能计算需求的日益增大, 越来越多的应用开始部署在以申威处理器为代表的国产高性能计算平台上. 这些应用中, 无论是在传统的科学计算、气象预报、金融统计等领域, 亦或是现今新兴的机器学习等, 均严重依赖底层BLAS库的实现以获得较高的计算性能. 而现有的开源BLAS库, 均无法有效的利用国产平台的硬件特性, 实际性能较低, 迫切需要针对国产平台进行优化实现的BLAS库出现. 因此, 结合神威蓝光等当前国产多核处理器体系结构特征, 研究BLAS数学库, 特别是3级BLAS函数的高性能实现方法具有重要意义.
1.2 本文组织结构
本文主要针对国家超级计算济南中心的申威1600平台进行BLAS数学库三级函数的优化研究工作,以通用矩阵相乘函数GEMM为例进行表述. 其中第一章是引言, 介绍平台信息与BLAS库优化现状以及本文工作的意义; 第二章以GEMM为例, 介绍三级BLAS函数特点; 第三章介绍基于单核的GEMM优化设计; 第四章介绍基于多核的GEMM优化设计; 第五章为实验, 与开源的GotoBLAS数学库进行性能比较;最后是总结与展望.
2 三级BLAS GEMM函数概述
一般来说, 1级BLAS函数计算复杂度为O(N), 2级BLAS函数计算复杂度为O(N2), 3级BLAS函数计算复杂度为O(N3), 评价一套BLAS数学库性能高低, 3级BLAS的性能是最重要的指标, 而通用矩阵乘法函数GEMM作为3级BLAS最常用的函数, 其性能指标往往也最被关注.
GEMM实现公式1所述的矩阵相乘计算, 其本质是K-N-M的三重循环计算, 计算复杂度为O(N3). 考虑其访存特性, GEMM函数读取A、B、C矩阵各一次,写回C矩阵一次, 复杂度可表述为O(2MN+MK+KN),整体为O(N2)复杂度, 在矩阵的K、N、M三维足够大的情况下, 计算复杂度远大于访存复杂度, 将访存开销隐藏在计算过程中是完全可行的, 理论上GEMM函数性能应可以接近平台性能峰值.
目前的通用编译器往往只能进行普适性的优化,例如循环展开, 利用硬件流水线进行加速, 而不能针对GEMM函数特性, 分析数据依赖情况, 实现最优化的计算与访存延迟互相掩盖. 例如著名的NETLIB BLAS, 一种通用的, 使用FORTRAN语言实现的BLAS库(一般作为正确性与性能的基准测试程序, http://www.netlib.org/blas/). 该BLAS库中的GEMM使用最朴素的三重循环实现, 可以认为除了编译器优化外不存在其它任何形式优化. 该版本BLAS在本文所述的申威1600平台上性能为280 MFLOPS, 仅仅相当于平台性能峰值的3.5%, 远不能满足应用对GEMM的性能要求[9], 故需要设计高效的分块算法, 结合核心段的需要手工汇编来实现.
3 基于单核的串行优化设计
针对申威1600平台单核, 基于其平台的扩展ALPHA指令集, 本节提出了GEMM函数的高性能优化方案. 该方案基于本文第2章所述的GEMM函数的计算密集型特征, 充分考虑申威1600平台特性, 最大程度发挥该平台计算能力, 实现该平台上的高性能GEMM函数, 合理利用平台的寄存器等硬件资源, 实现计算与访存延迟互相掩盖.
3.1 乘加指令
GEMM函数实现的计算如公式1所示, 对C矩阵元素进行乘加操作. GotoBLAS针对ALPHA架构的核心函数的汇编实现中没有实现乘加操作, 乘法与加法分别进行. 在寄存器分块为4*4的情况下, 读取A、B矩阵各4份数据, 计算16份C矩阵的部分解, 计算访存比达到4比1, 在内层循环充分循环展开后, 平均每4条计算指令中插入一条通信指令. 高达4比1 的计算通信会增加寄存器的消耗, 不利于软件流水线的排布.
申威1600平台提供SIMD乘加指令, 每次计算指令可以实现加法和乘法在一个指令周期完成. 在同样4*4的寄存器分块情况下, 计算通信比降低为2比1[10],计算指令总数减少一半, 理论上可达到2倍的性能加速, 内层循环中的中间变量数减少, 对寄存器的消耗降低, 利于软件流水线的排布.
3.2 256位的SIMD向量运算
一般而言, 在不考虑编译优化的情况下, 我们可以使用intrinsic函数进行手工向量化, 基于C代码就可以取得不错的性能提升. 但是对于性能要求较高的任务, 比如本文讨论的GEMM函数, intrinsic函数并不能胜任, 因为intrinsic函数不能控制指令的调度和寄存器分配, 所以我们需要在核心函数中编写向量化的汇编代码[9].
申威1600平台提供了256位的SIMD向量扩展支持. 以实数双精度为例, 每个元素为8字节、64位, 进行向量化扩展后, 配合长度为256位的浮点向量化寄存器, 每次顺序读取4个A矩阵元素, 同时对4个C矩阵元素进行运算, 理论上性能可实现4倍加速.
3.3 循环展开与软件流水线
循环展开是编译器经常使用的优化策略之一, 循环展开后, 最内层循环的单次循环内指令数增加, 从硬件角度看, 更多的指令可以用于乱序发射与乱序执行, 利于硬件流水线发挥作用, CPU保留站等硬件资源也可更充分得以利用; 从软件角度看, 更多的指令可以用于指令重排, 有助于避免“访存-计算”的数据依赖关系. 一般而言, 访问主存往往有较高的延迟, 要求多次的循环展开, 将访存操作的延迟隐藏于运算操作中.
在实际的核心函数实现中, 我们仍然采用了经典的N-M-K的计算顺序, 内层循环的部分代码如下, 其中VMAX为乘加指令:

图1 核心汇编代码举例
在核心函数设计过程中, 以下几点比较重要: (1)硬件提供两条流水线, 无数据依赖的计算与访存可同时发射, 则指令排布应尽量保证一条计算指令和一条取数指令共同出现, 使得两条流水线都占满; (2)最内层循环需展开足够的次数, 掩盖掉所有的本地访存指令, 考虑实际申威1600平台数据从cache到寄存器的延迟, 最内层的K层循环展开两次即可.
3.4 寄存器分块
寄存器分块的目的是合理安排核心函数中矩阵分块的大小, 在不超过硬件限制的情况下尽可能充分利用寄存器等硬件资源, 实现性能优化.
寄存器的数量决定了寄存器分块的大小. 申威1600是扩展的ALPHA架构平台, 每个CPU拥有F0到F31, 共32个逻辑浮点寄存器, 本文选择4*4的寄存器分块. 在此分块下, 每轮使用4个浮点向量寄存器, 取4个256位向量长度的A矩阵元素, 共16个A矩阵元素; 使用4个浮点向量寄存器, 每个寄存器取1个B阵元素并扩展成4份, 则4个寄存器处理4个B矩阵元素, 计算16个256位向量长度的C矩阵元素,即64个C矩阵双精元素的部分解, 由此共使用了24个浮点向量寄存器. 此外, F31寄存器固定存储0值,剩余7个逻辑寄存器存储中间变量或用作循环变量,寄存器资源使用合理且高效.
3.5 数据预取与数据重排
申威1600提供特定的预取指令fetchd, 支持将内存中的数据预取至cache中, 每次预取一个cache行的数据量. 若不使用预取指令, 每当一个cache行的数据使用完毕, 硬件都需要等待数据从内存加载至cache中,造成流水线停顿, 且这种停顿以百拍来衡量, 对于追求高性能的GEMM来说是无法容忍的. 在实测中, 若矩阵A拷贝过程不使用预取指令, 总体性能下降14.1%,若矩阵B拷贝过程不用预取指令, 总体性能下降43.6%.
使用fetchd预取指令的位置及预取跨步的大小需谨慎设计, 若跨步太小, 会造成数据还未完成预取就需要使用, 造成流水线停顿; 若跨步太大, 会造成预取数据完成后长时间没有使用, 再次被替换出去. 申威1600 CPU使用的cache替换顺序为FIFO, 即先进先出的策略, 这对GEMM函数的设计而言是有利的, cache数据的替换是可控的, 因此只要测试出合适的跨步, 性能可以保证稳定.
数据的预取仅考虑到指令位置与跨步大小是不够的. 按照Goto等人的分析[1,11], GEMM核心函数三重循环的最优顺序应是N-M-K, 且最内层循环, 即K层循环应保证足够高的性能, 尽量减少延迟, 最大程度利用好cache和寄存器等硬件资源, 否则函数整体性能无从谈起[12].
我们以列主元矩阵为例进行说明, 若矩阵数据不进行任何处理直接按照N-M-K的顺序进行计算, 使用前文所述的4*4寄存器分块, 不考虑SIMD向量化影响, 且假设分块矩阵的M维足够大, 则每次cache行只有前4个元素能够使用, 沿K维进行的下一次计算需要的数据一定不在该cache行中, cache资源被极大浪费, 且极易因cache不命中造成流水线停顿.
为此, 需考虑将A矩阵和B矩阵沿K维方向进行重排, 每次cache行所取数据都被完全利用, 重排效果如图2所示.

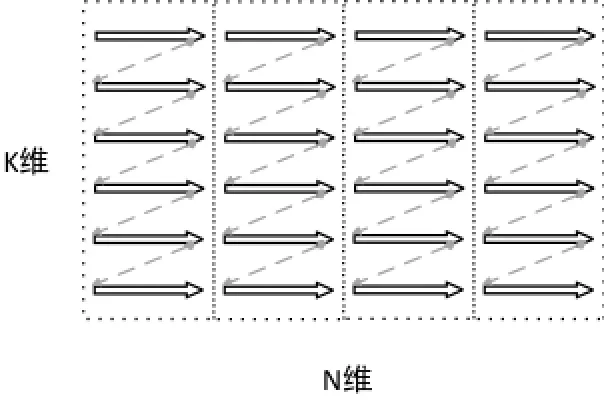
图2 A矩阵和B矩阵重排示意图
4 基于多核的优化设计
考虑计算任务的划分, 各线程对矩阵进行等份划分, 计算各自对应的C矩阵部分解即可, 理论上讲, 线程之间没有数据依赖关系, 可以说GEMM函数具有天然的多线程负载均衡特性. 对于GEMM函数而言, 进行多核并行化优化实施并不复杂, 每个计算核心运行一个线程, 每个线程之上的优化设计仍采用上一章所述的基于单核的优化设计方案即可.
直观来看, 任务划分可以按照A矩阵的M维进行划分或按照B矩阵的N维进行划分, 本文使用了行方向, 即沿着A矩阵的M维进行划分的方法, 4线程并行化的数据划分, 如图3所示, 每个线程计算对应的C矩阵部分解.
如图3所示, 4个线程各自拥有私有的部分A矩阵,线程间共享整个B矩阵, 计算对应的C矩阵的部分解.由于申威1600架构支持多线程共享内存, 理论上4线程对一个内存地址具有相同的访存延迟, 不会发生某个线程需要等待其他线程访存的情况.
正如前文所述, GEMM具有天然的负载均衡特性,在矩阵规模合理, 不考虑特殊规模或边界的情况下,可以做到所有线程计算规模完全或近似相等. 然而,由于每个线程内部的计算仍然按照单核进行, 仍需采用寄存器分块、软件流水线等技术, 每个线程需各自进行A、B矩阵的数据重排, 我们对A、B矩阵的重排情况分别进行讨论.

图3 线程间数据划分
首先考察A矩阵, 由于每个线程私有部分A矩阵元素, 线程内部进行的矩阵重排不会影响到其他线程,多个线程可以同时进行各自A矩阵的数据重排.
接下来考察B矩阵, 我们已知所有线程共享B矩阵的所有元素, 一种简单有效的方案是所有线程等待1号线程完成B矩阵的数据重排, 然后再并发进行计算. 但是这种方案破坏了GEMM本身具有的负载均衡特性, 在1号线程进行数据重排的过程中, 其他线程将进行等待; 另一方面讲, B矩阵的划分工作从直观上讲是完全可以并发执行的. 因此, 我们实际也需要将B矩阵划分于各个线程之中, 如图4所示, 将B矩阵按列划分于每个线程之中.

图4 B矩阵划分
考虑到B矩阵需要共享, 我们设计了一种二维数组的线程间共享的数据结构working[i], 表示第j个线程为第i个线程准备的重排后的B矩阵元素, working[i]中的每个元素为一个指针, 指向对应的重排后的B矩阵元素头指针. 换言之, 重排后的B矩阵数据被各个线程私有, 但这些数据指针却是共享的, 基于申威1600的平台多线程共享内存架构, 各线程可以相同的延迟共享这些数组.
该共享的数据结构内的元素为指针, 可用于线程间同步而无需另外设计线程间的锁机制, 当working[i]为空时, 表示此时的对应B矩阵还未重排准备就绪,不能用于计算, 该线程应该等待; 反之, 表示该B矩阵已重排准备完毕, 第i个线程可以获取第j个线程的B元素进行计算, 计算完毕后working[i]置为空, 等待下一轮的第j个B矩阵重排完毕. 同时, 只有working[all]都为空时, 第j个线程的B矩阵才算使用完毕, 没有其他线程需要这部分数据可以释放并进行下一轮的B矩阵数据重排.
5 性能测试与评价
申威1600平台作为国产高性能多核平台, 性能指标优异, 已被国家超级计算济南中心等国内超算中心使用, 该平台即为本文实验的测试平台. 该平台使用了扩展的ALPHA架构指令集, 每个CPU支持乘加指令与256位向量化运算, 支持计算指令与访存指令同步发射, 具体硬件参数如表1所示.

表1 申威1600主要参数
表2统计了统计基于单核的单线程方案, 数据规模分别为1024、2048、4096、8192, 申威1600 GEMM函数性能和GotoBLAS GEMM性能, 如图5所示. 实验涵盖了如上四种规模的实数单精、实数双精、复数单精、复数双精共计16组测试用例, 平均加速比为4.72, 最高加速比为5.61. 为说明基于申威多核的4线程设计方案加速效果, 表3统计了基于多核的4线程方案, 包含了数据规模与数据类型的同上的16组测试用例, 与申威平台单核的单线程方案相较, 平均加速比为3.02, 最高加速比为3.18. 对比图如图6所示.
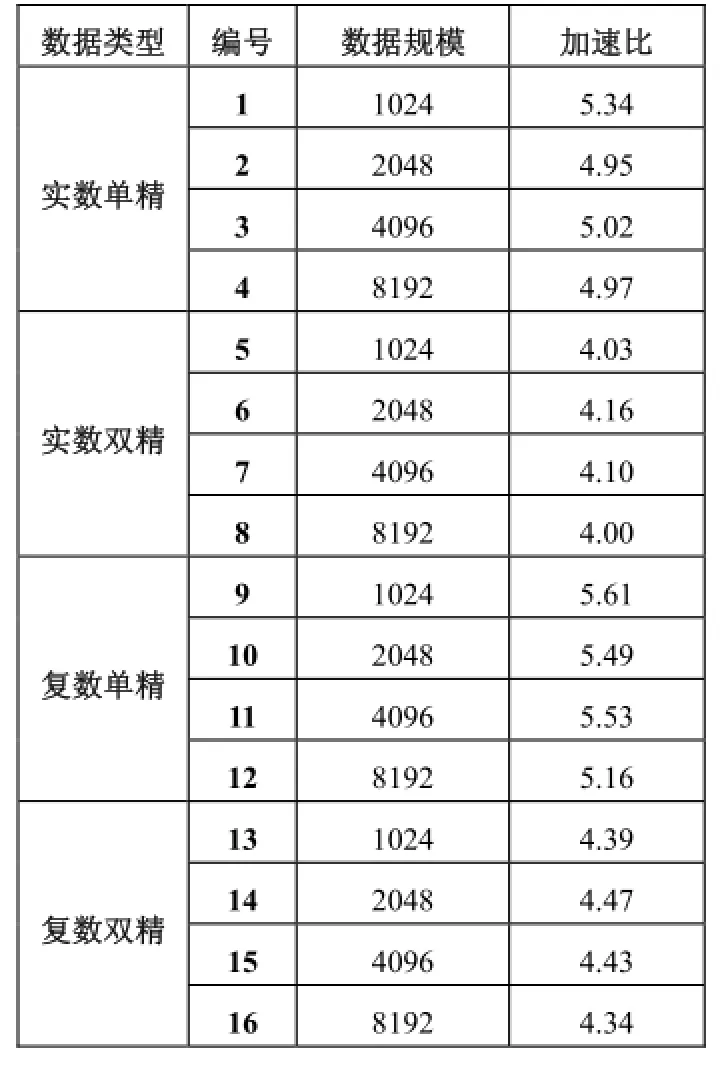
表2 申威单核与GotoBLAS单核性能对比
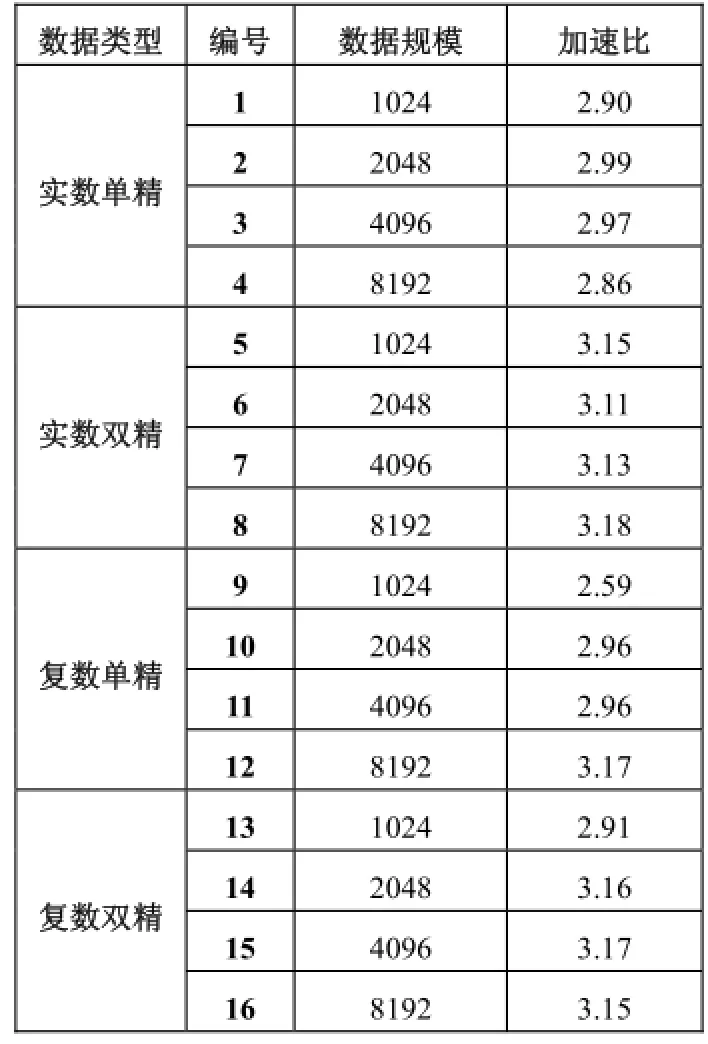
表3 申威多核4线程与申威单核性能对比
6 总结与展望
本文首先说明了三级BLAS GEMM函数的计算密集型的特征, 接下来介绍了国产申威1600多核平台的特征. 基于该平台扩展的ALPHA架构, 提出了基于该平台的高性能BLAS三级函数实现方案. 本方案首先分析了基于单核的单线程优化方案, 提出了矩阵数据重排、软件流水线、寄存器分块等基于该平台的优化技术;接着分析了基于多核的多线程优化方案, 提出了矩阵划分的方式与多线程同步机制. 在性能测试中, 基于申威1600平台优化过的GEMM函数性能, 在单核情况下对比GotoBLAS的平均加速比为4.72, 多核4线程方案的平均加速比为3.02, 达到了预期的效果.

图5 申威单核与GotoBLAS对比
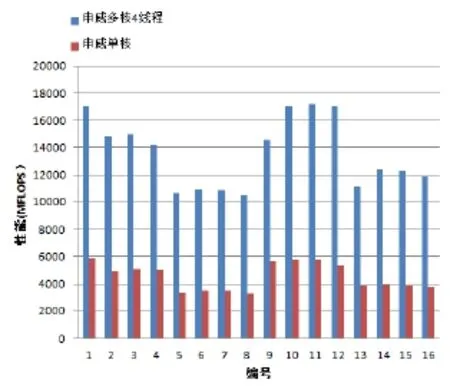
图6 申威4线程与单核对比
申威1600作为新兴的国产高性能计算平台, 我们期待着该平台系列的后续机型, 针对该系列平台未来将可能出现的新特性, 这对这些特性又会对高性能的BLAS数学库提出怎样的要求, 我们拭目以待.
1 Goto K, Geijn RA. Anatomy of high-performance matrix multiplication. ACM Trans. on Mathematical Software (TOMS), 2008, 34(3): 12.
2 Goto K, Van De Geijn R. High-performance implementation of the level-3 BLAS. ACM Trans. on Mathematical Software (TOMS), 2008, 35(1): 4.
3 蒋孟奇,张云泉,宋刚,等.GOTOBLAS一般矩阵乘法高效实现机制的研究.计算机工程,2008,34(7):84–86,103.
4 Whaley RC, Petitet A, Dongarra JJ. Automated empirical optimizations of software and the ATLAS project. Parallel Computing, 2001, 27(1-2): 3–35.
5 张帅,李涛,王艺峰,等.细粒度任务并行GPU通用矩阵乘.计算机工程与科学,2015,37(5):847–856.
6 Kurzak J.Preliminary results of autotuning GEMM kernels for the NVIDIA Kepler architecture-GeForce GTX 680 [z3.I, APACK Working Note 267,2014
7 李佳佳,张秀霞,谭光明,等.选择稀疏矩阵乘法最优存储格式的研究.计算机研究与发展,2014,51(4):882–894.
8 申威1600处理器的细枝末节.黑龙江科技信息,2011, (34):I0004–I0004.
9 张先轶.若干线性解法器多核和众核性能优化关键技术研究[学位论文].北京:中国科学院大学,2014.
10 李毅,何颂颂,李恺等.多核龙芯3A上二级BLAS库的优化.计算机系统应用,2011,20(1):163–167.
11 张先轶,王茜,张云泉,等.OpenBLAS:龙芯3A CPU的高性能BLAS库.2011年全国高性能计算学术年会(HPC china2011)论文集,2011.
12 陈少虎.BLAS库在龙芯3A上的实现与优化[学位论文].北京:中国科学院研究生院,2011.
Optimization of BLAS Level 3 Functions on SW1600
LIU Hao1,2, LIU Fang-Fang1, ZHANG Peng1,2, YANG Chao1, JIANG Li-Juan1,212
(Institute of Software, Chinese Academy of Sciences, Beijing 100190, China ) (University of Chinese Academy of Sciences, Beijing 100190, China)
BLAS is one of the most important basic underlying math library for scientific computing, in which the level 3 BLAS functions are most widely used. In this paper, we provide a high-performance method to implement Level 3 BLAS functions based on domestic Sunway 1600 platform. To make it clear, we take GEMM as an example. For the implementation on single-core, we apply many tuning techniques related to the specific platform, such as multiply-add instructions, loop unrolling, software pipelining and instruction rearrangement, SIMD operations, and register blocking to push up the performance. For the multi-core implementation, we propose an efficient multi-threaded method. Compared with GotoBLAS, one of the famous open-source BLAS, the experiments show that our serial single-threaded method achieves a speedup of 4.72. What’s more, the average speedup of 4-threaded execution towards the single-threaded one can also reach 3.02.
Sunway 1600; level 3 BLAS; GEMM; HPC; multi-core
国家自然科学基金(91530103,91530323)
2016-03-16;收到修改稿时间:2016-04-27
10.15888/j.cnki.csa.005456
