柔性车间调度的解空间距离聚类和变邻域搜索粒子群算法①

杜兆龙, 徐玉斌, 崔志华, 李建伟, 赵俊忠

(太原科技大学 计算机科学与技术学院, 太原 030024)

柔性车间调度的解空间距离聚类和变邻域搜索粒子群算法①

杜兆龙, 徐玉斌, 崔志华, 李建伟, 赵俊忠

(太原科技大学 计算机科学与技术学院, 太原 030024)

根据柔性车间调度问题提出基于解空间距离聚类和变邻域搜索的粒子群算法. 在粒子群算法基础上采用贪婪策略引入变邻域搜索方式, 即调整关键路径上最大关键工序的机器位置, 调整关键路径上工序相对位置变化, 加强局部搜索能力; 根据机器加工工序的空间距离, 采用K-means聚类得到机器加工工序“优良个体”, 加大局部搜索性能. 同时对于粒子群算法速度更新采用局部停滞策略, 保留局部片段相对位置不变特性. 通过实验仿真, 优化算法取得了较好的效果, 与一般的粒子群算法相比较收敛速度迅速且性能良好.

柔性车间调度; 变邻域搜索; 空间距离K-means聚类; 速度局部停滞

柔性车间调度是车间生产中的一类特殊形式. 所谓的柔性车间调度是指m台机器加工n件工件, 每个工件每个工序可以在多台机器上加工完成, 最终得到一种调度安排使得n种工件加工完成的时间最小的方案[1,2]. 该类问题因其随着工件和机器规模的扩大, 其求解规模伴随有爆炸性特点. 研究已经证实柔性车间调度问题是一类非确定多项式NP难问题[3]. 因此用直接查找算法很难获得较优的答案; 然而伴随着启发式搜索算法和群智能算法的发展, 则出现了越来越多的近似求解算法.

针对柔性车间的调度问题, 已有研究主要有: 遗传算法、粒子群算法、蜂群算法、蚁群算法、免疫算法等. 为了增强求解问题的能力, 相关学者进行了一系列研究. 曾建潮、崔志华等[4]提出一种基于主动调度编码的遗传算法, 实现将所有工序以不可重复的自然数进行编码, 优点是编码唯一且可行. 孔飞[5]提出的基于双层粒子群优化算法ITLPSO, 以工件号为工序编码, 相同工件的工序编码相同, 同时采用惯性权重w凸凹函数变化及其停滞阻滞策略, 在一定程度上加速收敛性能和搜索规模. 董蓉等[6]则提出一种以析取图模型为基础的混合GA-CAO算法, 在遗传算法结果基础上利用蚁群算法寻得较优的解. 徐华等[7]提出的DPSO算法使用基于NEH的最短用时分解策略避免早熟和提高全局搜索能力. 谢志强等[8]提出的动态关键路径策略和短用时调度策略实现以纵向为主兼顾横向的双向调度优化. 赵诗奎[9]提出基于空闲时间的邻域结构给出最大限度查询关键工序相关机器空闲时间的方法, 移动关键工序到空闲时间位置实现搜索优化.张国辉[10]对VNS-变邻域搜索进行了总结, 强调利用某种算法为VNS提供较好质量的初始解集. 高永超[11]参考的Big Valley分布理论和骨架尺寸的研究与讨论,其中Boose推断TSP等类似问题的最优解分布于一个大谷内. 孙元凯等[12]提出的解空间距离矩阵、衡量解空间规模的特征数和分隔因子、决定局部解空间崎岖形状的加工时间分布形式, 给出问题难易程度的衡量标准. 已有研究表明, 单一算法在全局或者局部搜索过程中都存在一定问题. 同时对于柔性车间调度问题本身特性的研究也有助于算法性能的提高.

由于柔性车间调度问题复杂性, 本文采用一种基于解空间距离聚类和变邻域搜索策略的PSO算法, 附加速度停滞控制, 在调度过程中不断优化机器工序位置, 以得到近似最优解.

1 问题描述

柔性车间调度问题, 是指具有m台机器, 加工n件工件的调度优化问题. 加工工件的机器集合为为第i台机器,i=1,2,3,...,m. 工件的集合为第j件工件,j=1,2,3,...,n. 每个工件的工序数和加工次序都是确定的, 对应于每个工件的工序集合, 如工件pj对应的工序数为nj, 故对应的工序集而所有工件对应的工序数集合对应第j个工件的总工序数. 工件的工序集在机器集上加工时间矩阵为大小为的矩阵. 如果工序不能在机器上加工, 设置相应的时间设置为0标记. 时间矩阵集合目标函数为最后一个被加工完的工件时间的最小值, 即:

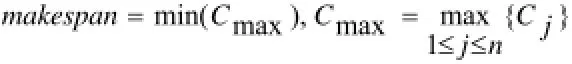
其中Cj为第j个工件加工完成时的时间.

同时在建模过程中假设:

1) 同工件同时刻至多一道工序在某台机器加工;

2) 同时刻某台机器至多加工一工件的一道工序;

3) 工件开始加工后必须完成该工件所有工序;

4) 工件加工按照确定的加工工序次序进行;

5) 每一工序只能在一台机器上加工, 不能选择多台机器.

2 基于解空间和邻域搜索策略粒子群算法

2.1 微粒群算法

Kennedy和Eberhart共同提出的微粒群算法[13],主要是针对于鸟类群体行为的觅食或者飞向栖息地的过程的建模. 在飞行进化过程中主要受个体速度惯性部分、个体认知部分、群体社会认知三部分影响. 标准的微粒群算法包括速度和位移两个进化公式:

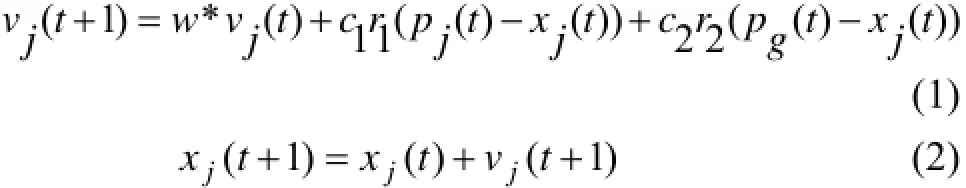
vj(t+1)为第(t+1)代第j个微粒的速度,xj(t+1)为第(t+1)代第j个微粒的位置, w为相应的惯性权重,c1为个体认知系数,c2为社会系数,为服从均匀分布的随机数;为第t代第j个微粒的个体历史最优位置,为第t代的群体历史最优位置.

针对车间生产调度, 首先是工序和机器的编码问题. 机器按照机器顺序编码. 工序编码是按照某工件当前出现次数表示该工件的工序数的编码方式. 如工件数2、机器数3, 每个工件都包含3道工序, 下面矩阵中第一行表示工序排列, 第二行表示对应工序加工所在机器排列. 矩阵第一列中工件号为1, 且第一次出现, 代表工件1的第一道工序, 机器号为2; 第四列中工件号也为1, 但是工件号1到当前位置已出现3次,故代表工件1的第三道工序, 机器号为1.

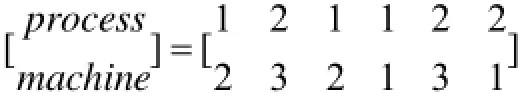
2.2 速度局部停滞控制

由Big Valley分布理论和骨架尺寸的研究与讨论, Boose推断TSP类似问题的最优解可能分布于一个大谷内, 因此对于调度方面问题也可以考虑对于局部进行特殊搜索.

定义1. 种群中个体对于本次进化, 其中某段或者某几片段的进化速度强制控制为0, 本次操作完成后,在下次的操作中再以极小概率选择部分片段再次进行强制控制, 这种控制称为速度局部停滞控制.

未选择控制部分, 其工序位置可以自由交换. 如果所有位置自由交换都出现障碍, 对于搜索则会陷入停滞. 用稀疏矩阵s(i,:)和概率均匀分布矩阵u(i,:), 共同对于工序变化速度进行选择, 当前第i个个体的速度停滞控制公式为:

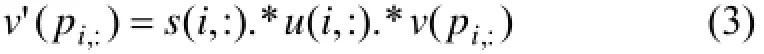
假设之前的速度和位置分别为

变化后的速度为

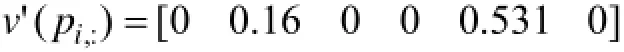
而新的位置更新得到p'=[12.16112.5312],对于重新排序的到p', 第一行为位置数值, 第二行为排序序号

按照新位置的大小重新排列得到[111222],同时修正对应的机器.

定义2. 由工件号重复多次出现的编码方式造成对工件工序排列时, 相同或者相邻工件的工序容易凑到一起“扎堆”, 较远的工件号与其交流出现一定障碍,需要归一化操作, 以消除由于编码产生的工件工序“扎堆”问题, 这一操作称为工序编码归一化.

如果工件1各个工序的编码都为1, 工件8各个工序编码都为8, 这时假设工件8的工序变化为process_8=8+v, 与工件号为1,process_1=1+v_1,如果对得到的工序位置进行排序的话, 其位置交流可能就会出现障碍, 导致工件编号越小其工序越容易出现在调度的前面, 工件编号越大其工序越容易出现在后面. 为了解决这个问题, 在进行粒子群算法位置更新前对当前工件工序排列进行归一化, 从而消除掉工件号编码的问题. 这里仅仅对工序编号进行归一化,而不对工序变化速度进行处理, 可以保留各个工件工序变化的特殊性, 而且速度在一定程度上是个体惯性、个体和群体三者的影响结合体. 工序编码归一化函数:

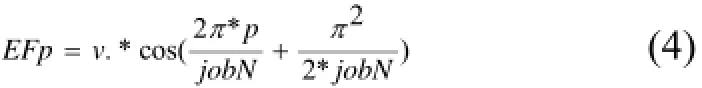
其中p为工序编码矩阵,jobN为工件数,v为工序的速度矩阵,EFp为归一化后的工序.

2.3 解空间K-means聚类

定义3. 如果将每个解都视为高维空间中的一个点, 并且在高维空间中对于这些多维向量排列, 每个解都会与部分解或无效解相邻, 由此构成的高维向量集合, 或者说是高维点阵集合, 称为问题的原空间[12].

定义4. 原空间中由可行解构成的集合称之为问题的解空间[12].

定义5. 对于车间生产调度问题而言, 取任意解s和t, 定义两解之间的距离[12]:

其中PRECi,s(j,k)表示解s中第i台机器上工序j和工序k之间的加工顺序, 如果j在k的前面则否则为逻辑异或运算符. 有是所有工件工序数之和, 在计算H(s,t)的时候采用的是工序的自然数编码.

公式(5)衡量两个解之间距离, 作为种群中某个解与当前最优解的距离计算公式. 通过研究发现当出现新的最优解时当前种群所有个体与最优解的距离的平均值可能会发生较大的波动, 之后又会趋于稳定直到下次出现新的最优值.

对于如何衡量单个个体的性能, 以种群中某个解在所有机器上工序的逆序数和的形式表示, 表示当前解的所有机器上的逆序数的总和, 如下

在机器i上,pi(j,k)为工序j,k逆序数表示, 如果工序j在k的前面, 那么pi(j,k)=0; 如果工序j在k的后面, 则pi(j,k)=1.

定义 6. 不同工件的工序, 如工件1的第2道工序, 和工件2,3,4,5等的第2道工序, 可以互称为顺位工序.

如果同一工件的工序, 在同一个机器上加工, 因为加工顺序问题不会存在逆序数; 但是不同工件的工序, 有可能产生逆序排列. 采用每台机器上工序逆序数的分析, 可以确认当前机器上不同工件间相同顺位工序被加工的次序, 如果相同顺位工序排列的很紧凑、位置很靠近, 则应该是一种较好的安排.

通过计算当前解在每台机器上工序的逆序数, 然后进行聚类分析可以衡量当前解的工件加工的工序对于寻找最优过程的影响.

2.4 变邻域搜索策略

基于变邻域搜索的邻域动作是由关键路径决定的,目前有Nowicki和Smutnicki提出的N5结构; Balas和Vazacopoulos提出的N6结构, 张超勇提出的N7结构.在搜索可行解的基础上采用机器调整和关键工序位置移动策略. 首先利用整个工序的排列顺序, 搜寻到相应的关键路径. 关键路径可能有多条, 仅选择其中的一条进行调整. 其次从关键路径中寻找到相应的最大花费工序, 简称最大关键工序. 每次进行最大关键工序的机器位置调整, 同时在关键路径上进行工序位置的移动.

机器策略:

(1) 对于最大关键工序进行机器调整, 选择该工序花费尽可能小的机器进行调整;

(2) 关键路径中工件的首道工序没在初始时刻开始加工的调整到某台机器的近似开始时刻;

(3) 关键路径中最后一道工序, 如果存在可以调整机器使得调整后整体时间缩短则调整.

关键路径上工序调整: 关键路径上两道工序为vw,...,vi,vi可以调整到vw之前, 除了该处位置的调整, 其它工序的相对位置不受影响, 但关键路径的时间被缩短, 只要满足以下条件之一:

(1) 如果vi为该道工件的首道工序, 可以直接移动;

(2) 如果vi的前道工序vi-1, 其完成的时间要比vw工序的完成时间早.

3 基于解空间和变邻域搜索的粒子群算法

3.1 初始化PSO种群和W的变化策略

初始化PSO种群, 个体数为N, 维数为所有工件的工序数之和, 种群个体随机产生. PSO惯性参数w采用凸凹函数形式:

3.2粒子群速度和位置更新

图1 算法流程图

对于机器更新, 假设之前机器位置如下所示m(t)=[232131], 按照之前介绍的粒子群进化公式, 可以得到m'(t+1)=[3.52.42.20.82.42.1]向上取整则m'(t+1)=[433132], 4超出了机器编码的范围, 可以修正为编号为1, 则更新后的新的机器编码为m(t+1)=[133132].

稀疏矩阵s(i,:)和概率均匀分布矩阵u(i,:); 粒子群速度v(pi,:), 位置pi等数值如下:

根据公式(3)当前第i个个体的速度更新为

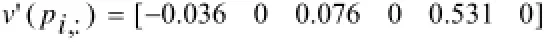
根据公式(4)归一化工序编码得EFp如下

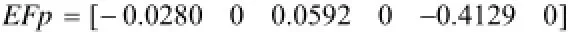
EFp代替pi, 由公式(2)更新工序位置得

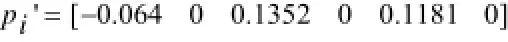
对得到的工序位置进行升序排列

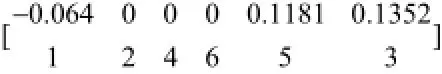
按照新位置顺序重新排列工序为[121221],同时修正对应的机器.

3.3 空间距离K均值聚类

根据空间距离计算的逆序数、机器加工工序数进行聚类. 逆序数则是每台机器上工序的逆序数, 种群中每个个体的逆序数为一组向量, 整个种群则构成一个逆序数矩阵. 机器加工工序数也是种群中每个个体由每台机器上加工工序数组合成一个向量. 采用K-means聚类算法, 聚类结果数位N1, 迭代次数为Niter, 去掉重复个体. 通过聚类可以将优良的个体替代掉“年老”个体, 将优良个体保持至下一代进行进化,提高优良个体的局部搜索范围.

3.4 VNS变邻域搜索

初始化VNS搜索的最大次数, 函数为

其中n为当次循环, N为循环最大次数.

在循环过程中首先搜索每个个体一条关键路径.在求解关键路径的同时, 将关键路径上最大关键工序查找出来. 将关键路径上最大关键工序进行相应调整,每次只调整(1)(2)(3)中的一种情况; 然后再根据关键路径上前后工序位置进行移动; 至此完成一次工序和机器的内部调整, 接着开始下次VNS循环.

4 实验分析

4.1 实验设计

为了验证实验效果, 采用Intel双核处理器I5-5200U@2.20GHZ, 内存4GB, 64为操作系统, MATLAB为实验仿真工具, 采用数据集为Kacem、Hurink[14]、Brandimarte[14]等.

算法的参数设置: 种群中个体数N=60, 惯性参数W的范围[0.1,0.9], c1=1.5,c2=1.5,r1,r2采用范围在(0,1)之间的随机数, 惯性权重更新采用上文介绍的抛物线形式,整体迭代次数N=100, 当前迭代次数为n, 因此每次VNS邻域搜索的次数最大值设置count＜=20限制.

4.2 仿真结果

基于速度停滞控制、空间距离聚类及变邻域搜索的粒子群算法简称为SVNS-vPSO. 对于Kacem基准问题的10*10样例, 其迭代过程中的H(s,t)距离均值变化曲线如图2所示, 在当次种群迭代中寻得较优值时会发生H(s,t)均值跳动反应. 因此搜索的结果极可能存在于这些跳动位置处种群局部最优个体身上.

对于Kacem基准问题的8*8算例, SVNS-vPSO算法生成的最优调度甘特图如图3. 图4为Kacem问题集的本算法收敛曲线. 表1为本算法下Kacem各个实例的具体运行数据. 对于图4和表1表明算法能够在较短时间与迭代次数内获得最优解.

图2 Kacem 10*10的H(s,t)均值变化曲线

图3 Kacem 8*8调度优化甘特图

图4 Kacem数据的算法收敛曲线

表2中对于PSO算法、ITLPSO双层粒子群算法[5]、AL+CGA(局部最小化分配模型的进化算法)、改进GA、GA-ACO遗传蚁群算法, 其中后三种算法参数设置按董蓉文中[6]参数形式, 最后搜索的结果如表2, 由数据可见SVNS-vPSO算法的搜索最优和平均值较一般的粒子群算法较好, 但是在平均计算时间和平均结果上和AL+CGA、改进GA算法比较而言相似甚至有些数据优于它们, 但是较GA-ACO算法稍差些.

表1 Kacem各实例的计算结果统计

表2 Kacem基准问题各方法运行30次结果比较

表3和表4中数据集来自于参考引用[14]网页中的FJSPLIB文件. 这里选用Hurink数据集和Brandimarte数据集中数据进行测试. 表中n代表工件数, m代表机器数, C**表示当前的最优值, Cmin为本文算法获得的最优值, RD(%)为本文算法最优值与C**的相对误差,其具体公式为:

表3 Hurink数据集[14]运行结果

表4 Brandimarte数据集[14]运行结果

由表3和表4测试结果表明, 该算法取得一定效果. 对于Hurink数据, 当工序数达到一定程度后, 相对误差开始增大; 对于Brandimarte类型数据, 其相对误差值高些.

实验仿真结果表明, 当工序数少时如Kacem问题,可以快速搜索到有效的结果; 当工序数增大后其效果将会出现一定偏差, 如Hurink和Brandimarte的数据.算法中对工序和机器分别编码, 然后进行PSO算法速度和位置更新, 但进化过程中两者只有一个约束关系,即工序能不能够在此机器上加工. 也就是说工序和机器的进化两者近似于彼此独立, 缺少进化的有效协同,无法形成统一整体. 对工序和机器进行整体编码的方式, 可以解决类似的问题, 但其设计方法则更困难.

5 结语

本文对于柔性车间调度问题提出了SVNS-vPSO算法. 即通过解空间距离K均值聚类、贪婪变邻域搜索、粒子群停滞控制等策略提高了优化算法的收敛速度和搜索结果. 通过研究发现, 工序与机器之间彼此近似孤立进化, 将影响整体的搜索结果. 下一步对工序和机器进化进行协同研究, 或者是采用工序和机器整体编码的方式[15]研究. 同时对于机器使用率和整体加工时间等多目标优化问题可以通过基于空间距离、机器逆序数等因素进行优化研究.

1 Brucker P, Schlie R. Job-Shop scheduling with multipurpose machines. Computing, 1990, 45(4): 369–375.

2 Mati Y, Rezg N, Xie XL. An intergrated greedy heuristic for a flexible job shop scheduling problem. Proc. of IEEE International Conference on Systems, Man, and Cyberneticcs. Washington, D.C., USA. IEEE. 2001. 2534–2539.

3 Blazewica J, Finke G, Haaopt G, et al. New trends in machine scheduling. European Journal of Operational Research, 1988, 37(3): 303–317.

4 曾建潮,崔志华,等.自然计算.长沙:国防工业出版社,2012.

5 孔飞,吴定会,等.基于双层粒子群优化算法的柔性作业车间调度优化.计算机应用,2015,35(2):476–480.

6 董蓉,何卫平.求解FJSP的混合遗传-蚁群算法.计算机集成制造系统2012,18(11):2492–2501.

7 徐华,张庭.改进离散粒子群算法求解柔性流水车间调度问题.计算机应用,2015,35(5):1342–1347,1352.

8 谢志强,杨静等.基于工序集的动态关键路径多产品制造调度算法.计算机学报,2011,34(2):406–412.

9 赵诗奎,方水良,等.作业车间调度的空闲时间邻域搜索遗传算法.计算机集成制造系统,2014,20(8):1930–1940.

10 张国辉.柔性作业车间调度方法研究[博士学位论文].上海:华中科技大学,2009.

11 高永超.智能优化算法的性能及搜索空间研究[博士学位论文].济南:山东大学,2007.

12 孙元凯,刘民,等.调度问题及其解空间的特征分析.电子学报,2001,29(8):1042–1045.

13 Eberhart R, Kennedy J. New optimizer using particle swarm theory. Proc. of the Sixth International Symposium on Micro Machine and Human Science, MHS’95. IEEE, Piscataway, NJ, USA. 1995. 39

14 http://people.idsia.ch/～monaldo/fjsp.html.

15 Singh MR, Mahapatra SS. A quantum hehaved particle swarm optimization for flexible job shop scheduling. Computer & Industrial Engineering. 2016, 93: 36–44.

Solution Space Distance Clustering-Variable Neighborhood Search Particle Swarm Optimization for Flexible Job Shop Scheduling Problem

DU Zhao-Long, XU Yu-Bin, CUI Zhi-Hua, LI Jian-Wei, ZHAO Jun-Zhong
(Department of Computer Science and Technology, Taiyuan University of Science and Technology, Taiyuan 030024, China)

Based on the Flexible Job-Shop Scheduling Problem(FJSP), an improved particle swarm optimization algorithm is proposed, which is based on solution space distance clustering and variable neighborhood search. In this algorithm, a better solution to the problem is that the greedy strategy is adopted to introduce a variable neighborhood search method, adjusting machine location of the biggest key processes on the critical path, adjusting the relative position changes which is on the critical path. According to the space distance of the machining process, the K-means clustering is used to get the “excellent individuals” of machine processing, increasing the local search performance. At the same time, the speed of the particle swarm optimization is updated with the local self-adaptive stagnation strategy, and the relative position of the local segment could be kept unchanged. Through the experimental simulation, the optimization algorithm achieves good effectiveness, and the convergence speed is rapider and the performance is better compared with the general PSO algorithm.

flexible job shop scheduling problem; variable neighborhood search; space distance K-means clustering; velocity local stagnation

2016-03-14;收到修改稿时间:2016-04-29

10.15888/j.cnki.csa.005482