钛合金相变点预测模型的构建和评估
2016-02-17任军帅张英明吝靖玉席恩平
任军帅,张英明,吝靖玉,席恩平
(西北有色金属研究院,陕西 西安 710016)
钛合金相变点预测模型的构建和评估
任军帅,张英明,吝靖玉,席恩平
(西北有色金属研究院,陕西 西安 710016)
基于西北有色金属研究院实际生产中统计的321组钛合金铸锭化学成分与相变点数据,构建了预测钛合金(α+β)/β相变点的人工神经网络模型和多元线性回归模型,并对模型的准确性进行了评价分析。结果显示,多元线性回归模型的训练值及预测值与(α+β)/β相变点实际值的相关性系数分别为0.761 05和0.809 93,而人工神经网络模型的相关性系数分别为0.927 21和0.818 51,具有更好的相关性。人工神经网络模型的平均绝对误差为4.02 ℃,相比多元线性回归模型(平均绝对误差为5.11 ℃)具有更高的精度,可以更好地描述合金元素与钛合金(α+β)/β相变点之间的非线性关系。
钛合金;相变点;合金元素;多元线性回归模型;人工神经网络模型
0 引 言
(α+β)/β相变点是确定钛合金锻造温度的重要参数,通常定义为钛合金组织中α相正好完全消失时的温度。钛合金(α+β)/β相变点受其合金元素,尤其是C、N、O、H等间隙元素的显著影响,各批次钛材均需单独准确测定。目前,实际生产中主要采用连续升温金相法、膨胀法等实验方法测定相变点,均需要制备大量的试样及特定的设备,周期长、成本高。因此,基于合金元素含量计算钛合金(α+β)/β相变点的方法引起国内外学者广泛关注。C.F.Yolton、F.H.Froes等[1]采用多元线性回归(Multiplelinearregression,MLR)方法得到的钛合金(α+β)/β相变点计算公式如下:
T(α+β)/β=872 ℃+∑fiXi
(1)
式中,Xi为元素含量,fi为元素含量对(α+β)/β相变点的影响系数。但是该公式包含的元素种类不全,尤其是没有包含对相变点有显著影响的C、N、H、O间隙元素,会引起较大的计算误差。目前,国内应用较为广泛的钛合金相变点计算公式如下[2]:
T(α+β)/β=885 ℃+∑fiXi
(2)
式中885 ℃代表纯钛的相变点。该公式由多元线性回归模型得到,模型中包含了影响钛合金相变点的主要元素。由于多元线性回归模型将合金元素与(α+β)/β相变点的关系近似为为线性关系,无法反应出合金元素之间的交互影响,因此在实际应用时误差较大,大多用于定性分析。
人工神经网络模型(Artificialneuralnetwork,ANN)作为一种高容错的非线性动态系统,近年来获得迅速发展,广泛用于解决各种复杂非线性问题。目前,应用最为广泛的神经网络模型是由Rumelhart和McClelland提出的多层前馈神经网络(BP-ANN),其训练过程基于网络误差的最速下降算法,通过误差逆向传播的形式不断反复调整各处理单元的权值和阀值,直到输出误差减小到预期值。BP-ANN模型已被广泛应用于钛合金领域的相关研究,包括构建钛合金本构关系模型[3-4]、力学性能预测[5-6]、合金组织及相变规律研究[7-8]等。而利用BP-ANN模型对合金元素与相变点关系的研究相对较少,国内只有孙宇等[9]基于人工神经网络模型,利用期刊中收集的数据,建立了钛合金相变点的BP人工神经网络预测模型,结果显示其精度显著优于传统经验公式。国外的Z.Guo[10]、P.S.NooriBanu[11]分别利用ANN模型,构建了合金元素与钛合金(α+β)/β相变点的关系,并研究了合金元素对相变点的非线性影响。
为了实现通过化学成分短周期、快速、准确预测钛合金相变点,提高生产效率,降低检测成本,本研究基于实际生产中的钛合金成分及相变点数据,分别构建钛合金(α+β)/β相变点的多元线性回归模型和人工神经网络模型,并对两种模型的预测效果进行对比评价,为生产中相变点的预测提供参考。
1 MLR模型及BP-ANN模型构建
1.1 数据统计
模型构建所用数据为西北有色金属研究院实际生产中统计的钛合金铸锭成分及(α+β)/β相变点,共计321组数据。铸锭牌号包括TA7、TA15、TC4、TC4ELI、TC6、TC11,合金元素涵盖影响钛合金相变点的主要元素——Al、V、Fe、C、N、O、H、Si、Mo、Zr、Sn、Cr,共计12种。从321组数据中随机选取257组数据(约占总数的80%)用于模型构建,剩余64组数据(约占总数的20%)用于测试所构建模型的预测效果。表1为用于训练和测试的合金元素含量范围。

表1 训练及测试数据种类及范围
注:训练数据(α+β)/β相变点范围为965~1 042 ℃,测试数据相变点范围为967~1 025 ℃。
1.2MLR模型构建
基于257组训练数据,采用Origin软件的MultipleLinearRegression命令,多元线性拟合合金元素含量和(α+β)/β相变点,从而得到合金元素与(α+β)/β相变点的MLR模型。式(3)为多元线性回归结果:
T(α+β)/β=989 ℃+2.1[Al]-9.5[V]+9.6[Fe]+ 205.5[C]+79.8[N]+152.7[O]- 1 861.6[H]-12.5[Si]-3.4[Mo]- 3.1[Zr]+0.3[Sn]-20.3[Cr]
(3)
MLR模型构建完成后,将剩余的64组测试数据作为输入值,代入公式(3)中预测钛合金相变点,从而测试所构建多元线性回归模型的精度。
1.3BP人工神经网络模型构建
基于MATLAB软件构建BP人工神经网络模型,采用三层网络结构,输入层、隐含层和输出层之间的传递函数分别设定为tansig和purelin。以12种合金元素含量为BP人工神经网络模型的输入参数,合金的(α+β)/β相变点为输出参数,共计257组数据作为训练数据。为了避免BP人工神经网络在反复迭代计算中发生数值溢出的问题,对神经网络的各输入参数进行归一化处理,即将输入参数值映射到(0,1)内,采用公式为:
(4)
式中,X代表各输入的合金元素,Xmax和Xmin为各合金元素含量的最大值与最小值。
所构建BP人工神经网络模型的隐含层网络节点数经过反复试验,择优选择,最终确定隐含层节点数为25。网络训练的目标误差(goal)为10-8,最大训练步数(epochs)为105。图1为构建的BP人工神经网络模型结构图。

图1 BP人工神经网络模型结构图Fig.1 Neural network architecture of BP-ANN model
BP人工神经网络模型构建完成后,将剩余的64组数据作为测试数据,用其预测钛合金相变点,并将结果与实际值进行对比分析。
2 MLR模型及BP-ANN模型评价
从式(3)可以看出,所构建的MLR模型中,除Fe元素外,其他元素对相变点的作用与已有文献[2]结果一致。α稳定元素Al、C、N、O更多的固溶于α相中,可以显著提高钛合金(α+β)/β相变点。β稳定元素V、H、Si、Mo、Cr则对β相起到固溶强化的作用,从而使钛合金(α+β)/β相变点降低。Zr和Sn属于中性元素,在α相和β相中都有较大固溶度,Sn对钛合金(α+β)/β相变点影响不大,而Zr对相变点则有较大的影响,其含量每增加1%,钛合金(α+β)/β相变点降低3.1 ℃,与文献[9]结果一致。
图2为MLR模型计算值与合金相变点实际值的相关性曲线。BP人工神经网络模型计算值与合金相变点实际值的相关性曲线则如图3所示。图中虚线为A=T的理想直线,代表所有(α+β)/β相变点拟合值与实际值相等,模型结果的相关性曲线(实线)与理想直线越接近,则代表训练或预测结果越精确。从两组图可以直观的看出,BP人工神经网络模型的精度要高于MLR模型。

图2 MLR模型计算值与实际值线性拟合图Fig.2 Linear regression between output data and actual data for MLR model
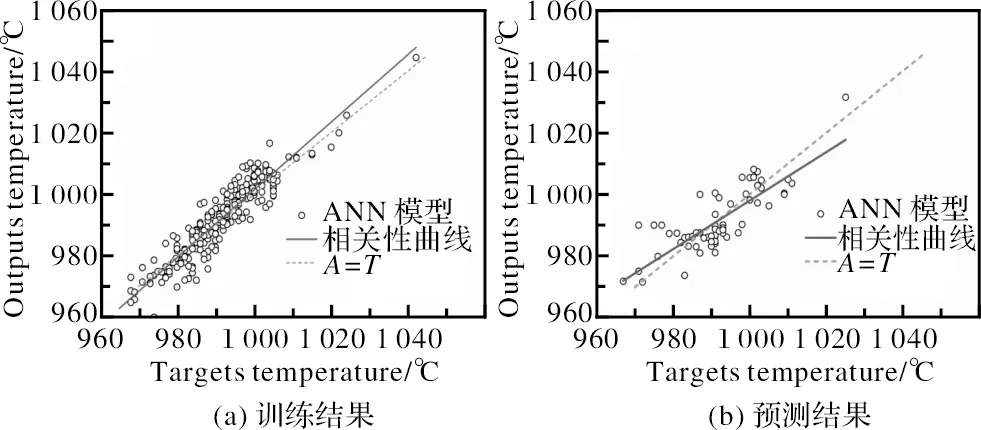
图3 BP-ANN模型计算值与实际值线性拟合图Fig.3 Linear regression between output data and actual data for BP-ANN model
为了进一步定量评价所构建两种(α+β)/β相变点预测模型的效果,采用统计学中的拟合相关性系数R、绝对误差e来综合衡量模型的精度。
(5)
(6)
根据式(5),求得所构建MLR模型训练值及预测值与(α+β)/β相变点实际值的相关性系数分别为0.761 05和0.809 93,而BP人工神经网络模型的相关性系数分别为0.927 21和0.818 51。相关性系数R表征模型预测值和实际值之间相关关系的强弱程度,R的绝对值越接近于1,则相关性越强。因此,BP人工神经网络模型具有更好的相关性。
将训练及预测结果代入公式(6),得到MLR模型、BP-ANN模型计算值与实际值之间的绝对误差分布,见图4。可以看出,BP人工神经网络模型训练及预测数据的绝对误差更为均匀的分布于误差e=0线两侧。将绝对误差值求和取平均值,得到所构建MLR模型、BP人工神经网络模型的平均绝对误差,分别为5.11、4.02 ℃。为了与传统经验公式对比,将321组数据代入式(2),计算得到传统经验公式的整体平均绝对误差为22.35 ℃。很显然,基于实际数据所构建的MLR模型的精度要显著高于传统经验公式,同时BP人工神经网络模型在预测精度上比MLR模型更具优势。
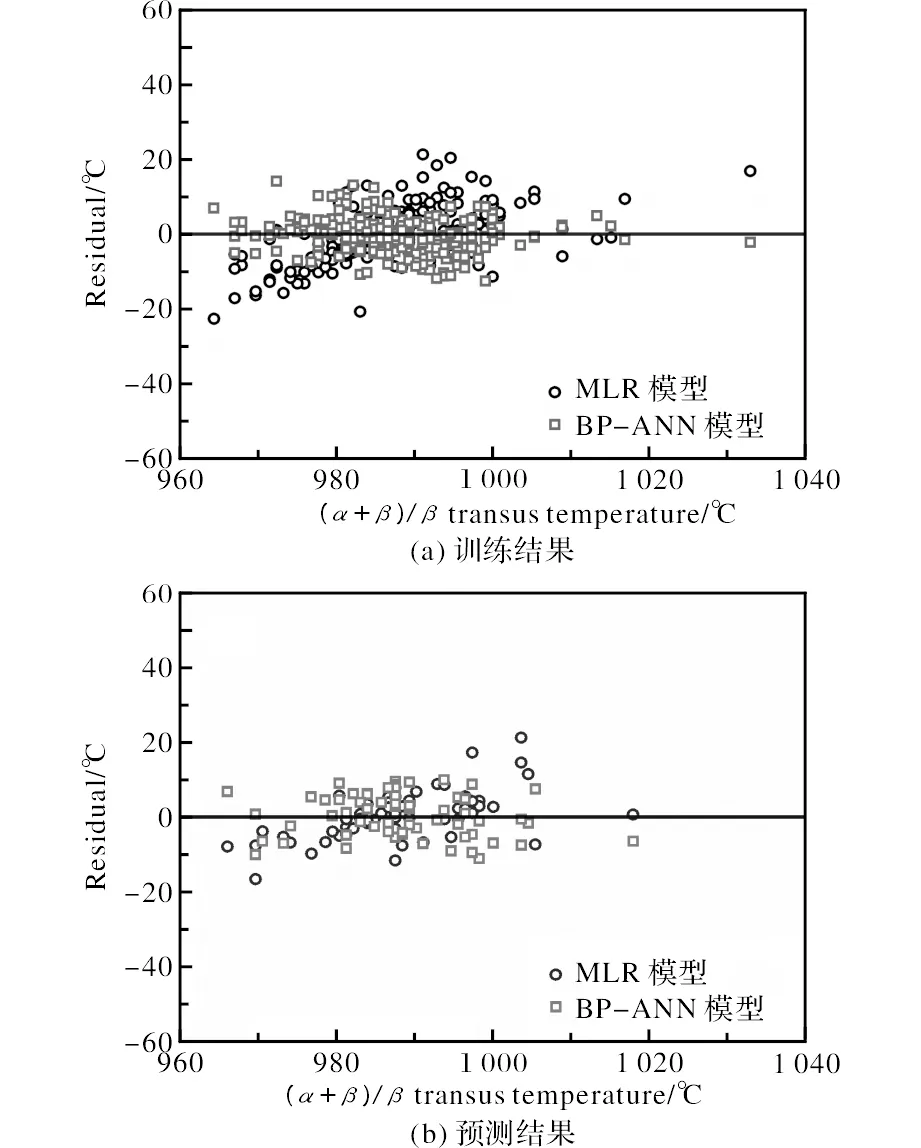
图4 MLR模型、BP-ANN模型计算值与实际值的绝对误差分布图Fig.4 The absolute error distribution between output data and actual data of MLR model and BP-ANN model
3 结 论
(1)基于实际生产中统计的321组钛合金成分与相变温度数据,分别利用人工神经网络和多元线性回归构建了合金元素对钛合金(α+β)/β相变点的影响模型。
(2)多元线性回归模型的平均绝对误差为5.11 ℃,人工神经网络模型的平均绝对误差为4.02 ℃。神经元网络作为一种高容错的非线性动态系统,可以更准确的体现(α+β)/β相变点与合金元素间复杂的非线性关系。
[1]YoltonCF,FroesFH,MaloneRF.Alloyingelementeffectsinmetastablebetatitaniumalloys[J].Metallurgical&MaterialsTransactionsA, 1979, 10(1):132-134.
[2] 稀有金属材料加工手册编写组. 稀有金属材料加工手册[M]. 北京:冶金工业出版社, 1984:48.
[3] 鲁海洋, 孙宇, 朱艳春,等. 基于神经网络的BT20钛合金本构关系模型[J]. 钛工业进展, 2010, 27(4):20-24.
[4]PengW,ZengW,WangQ,etal.Comparativestudyonconstitutiverelationshipofas-castTi60titaniumalloyduringhotdeformationbasedonArrhenius-typeandartificialneuralnetworkmodels[J].Materials&Design,2013,51(5):95-104.
[5] 孙宇,曾卫东,赵永庆,等.基于BP神经网络的置氢TC21合金力学性能预测[J]. 稀有金属材料与工程, 2012, 41(6):1041-1044.
[6] 岳洋, 朱景川, 刘勇,等. 基于BP神经网络的TA15钛合金热变形工艺-性能预报[J]. 稀有金属材料与工程, 2009, 38(10):1811-1814.
[7] 邵一涛, 曾卫东, 韩远飞,等. 基于BP人工神经网络的TC17钛合金显微组织-力学性能关系预测[J]. 稀有金属材料与工程, 2011, 40(2):225-230.
[8] 段园培, 李萍, 薛克敏,等.TB8钛合金固溶组织研究及神经网络预测[J]. 稀有金属材料与工程, 2012, 41(8):1426-1430.
[9] 孙宇, 曾卫东, 赵永庆,等. 应用人工神经网络研究化学元素对钛合金相变点的影响[J]. 稀有金属材料与工程, 2010, 39(6):1031-1036.
[10]GuoZ,MalinovS,ShaW.Modellingbetatransustemperatureoftitaniumalloysusingartificialneuralnetwork[J].ComputationalMaterialsScience, 2005, 32(1):1-12.
[11]BanuPSN,RaniSD.Betatransuspredictionoftitaniumalloysthroughintegrationofartificialneuralnetworkandmultifactordimensionalityreductionanalyses[J].MaterialsDiscovery,2015,2:16-23.
Construction and Evaluation of the Prediction Models of Titanium Alloys’ (α+β)/βTransusTemperature
Ren Junshuai, Zhang Yingming, Lin Jingyu, Xi Enping
(Northwest Institute for Nonferrous Metal Research,Xi’an 710016, China)
In this paper, artificial neural network (ANN) and multiple linear regression (MLR) model were developed and analyzed based on 321 sets of data, incuding alloying elements and (α+β)/βtransusdatafromNorthwestInstituteforNonferrousMetalResearch,andtheaccuracyofbothmodelswereevaluated.ResultsshowthatthecorrelationcoefficientsbetweentheMLRmodel’strainingdataand(α+β)/βtransus,thepredictiondataand(α+β)/βtransuswere0.761 05and0.809 93,respectively.ThecorrelationcoefficientsbetweentheANNmodel’strainingdataand(α+β)/βtransus,thepredictiondataand(α+β)/βtransuswere0.927 21and0.818 51,respectively.ANNpredictionsareinbetteragreementwiththeexperimentaldata.ThemeanabsoluteerroroftheMLRmodelis5.11 ℃,andthemeanabsoluteerroroftheANNmodelis4.02 ℃.ANNmodelcanmoreaccuratelydescribethenon-linearrelationshipbetween(α+β)/βtransustemperatureandalloyingelements.
titanium alloys;transus temperature; alloying elements; multiple linear regression; artificial neural network
2016-06-15
任军帅(1989—),男,工程师。
TG146.2+
A
1009-9964(2016)06-0028-04
