基于边界逼近的肺实质分割方法
2016-02-17黄智定
黄智定 孙 红,2,3*
1(上海理工大学光电信息与计算机工程学院,上海 200093)2(上海理工大学管理学院,上海 200093)3(上海现代光学系统重点实验室, 上海 200093)
基于边界逼近的肺实质分割方法
黄智定1孙 红1,2,3*
1(上海理工大学光电信息与计算机工程学院,上海 200093)2(上海理工大学管理学院,上海 200093)3(上海现代光学系统重点实验室, 上海 200093)
肺部CT图像的分割是计算机辅助诊断系统处理的一个重要环节,其分割的结果影响到医生的诊断与进一步的分析。由于胸膜结节的灰度与肺实质外围的灰度相近,运用传统的分割方法无法正确分割出此类病灶。将胸膜结节包含肺实质一起分割出来,使计算机辅助诊断系统能够对此类病灶做进一步的分析。提出一种结合Graham算法以及边界逼近的方法,对肺实质的轮廓进行修正,进而得到修正的二值模板;将该模板与原图像做乘运算,得到包含胸膜结节的肺实质。运用所提出的方法,对公开数据库LIDC中68张含病灶的CT样本图像做处理,通过与传统方法的对比以及对算法的过分割比例、欠分割比例以及准确性的分析,得到准确率为98.5%,平均过分割比例为1.35%,平均欠分割比例为0.51%,证明了该方法的有效性。
医学图像处理;肺结节;计算机辅助诊断
引言
肺结节是肺部常见的病变之一,早期诊断、治疗是降低肺癌死亡率的关键。目前肺结节的主要检测手段是CT扫描,孤立性肺结节在CT影像中主要表现为直径不大于3cm的圆形或类圆形病灶。然而,由于肺内器官组织的复杂性,胸膜表面的肺结节呈现不同的特征,有些甚至无法通过肉眼轻易识别。仅一位患者的CT图像就多达300张,人工读片将耗费大量的时间,且容易遗漏或者误诊。由于计算机辅助诊断的精确性越来越高,自动检测的方法被越来越多的医师所采纳,不仅降低了医生的工作量又可以帮助医生快速做出诊断。肺部CT图像的分割是计算机辅助诊断中的一个重要环节。分割的好坏直接影响到系统做进一步分析的精确性。运用传统的方法(如阈值分割法、活动轮廓模型、水平集方法),都无法正确地将胸膜结节包含在肺实质内部一同分割出来[1],从而遗漏了对这些病灶的检测。为了克服这个问题,许多学者提出了对胸膜结节的分割方法:Armato等[2]提出一种滚球模型算法,用一个半径为R的球在肺实质轮廓上按某一方向滚动,当球与轮廓表面的切点数大于1时,认为此处存在胸膜结节并对该轮廓进行补正;此方法中滚球的半径是固定的,固定的半径值通常会造成区域的过分割,即将非肺叶部分也一同分割出来,降低了算法的精度。Pei等[3]将肺实质的轮廓分为胸膜外轮廓以及接近心脏和隔膜的内轮廓,外轮廓运用凸包算法修正,内轮廓通过判断来自中心点的射线与内轮廓的交点距离来舍弃原轮廓的点并连接所有保留点达到修正的目的,此方法对于内轮廓上产生病灶的样本图像经常做出欠分割或者过度分割。Shen等[4]提出一种双向链码的算法对边界点进行筛选,并将这些候选点输入训练好的SVM分类器中,得到需要进行轮廓修补的边界点,并用直线将它们相连,从而达到边界补正的目的;取得的分类效果非常好,但由于肺部结构的复杂性以及边界的不确定性,对于一些比较特殊的将连通的肺实质区域断开的胸膜结节,该算法无法对边界进行补正;SVM的训练需要对样本进行标注,将耗费大量的时间。李金等[5]提出一种改进的凸包扫描算法,用来得到肺实质区域的最大凸多边形,并选取两个凹陷端点连线的中点的灰度差与固定阈值作比较,从而排除过分割的区域;该方法的优点是执行效率较高,主要的缺点是对于内轮廓上出现病灶的样本经常做出欠分割,从而影响算法的精确性。Pu等[6]提出一种自适应边界匹配的方法,给定一个匹配步进,在其内运用右手螺旋定则寻找到最小凸多边形;判断凹陷的宽与深度的比值是否小于一个固定阈值,若满足条件则缩小匹配步进继续判断,若不满足则判定边缘凹陷为病灶并进行补正;此方法具有分割准确率高、误分割比例低、自适应强等优点。
在本研究中,提出一种新的方法:基于Graham凸包算法,结合边界逼近的方法,对肺实质轮廓进行修正,从而得到一个修正的二值模板,用该模板与原图像做乘运算后,即可得到包含胸膜结节的肺实质的分割图像。本算法的流程如图1所示。

图1 算法流程Fig.1 The flowchart of algorithm
1 方法
1.1 预处理
运用OTSU算法对原图像做二值化处理,预处理效果如图2所示。
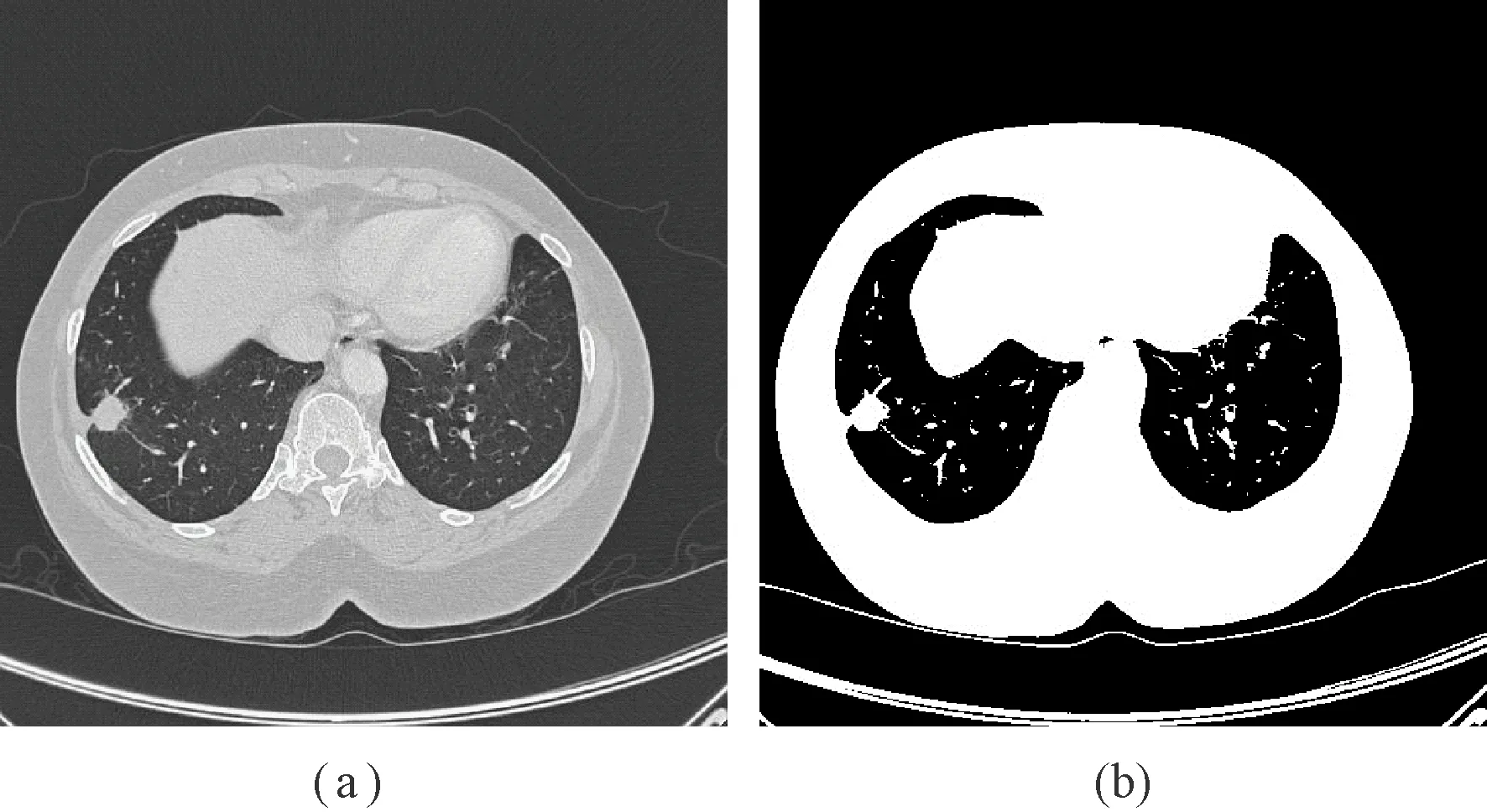
图2 预处理。(a)原图像;(b)OTSU阈值分割Fig.2 preprocessing(a)Original image(b)OTSU threshold segmentation
1.2 Graham算法
凸包是图形学中的概念,指的是在一个平面上分布着若干个点,希望找到一个点的集合,连接集合中的点所得到的最小的多边形可以包含该平面上的所有点,这个多边形就称为这个点的集合的凸包。笔者希望通过这种方法来得到包含图3(a)中轮廓的最小凸多边形,即图3(b)所示。

图3 肺实质轮廓。(a)处理前;(b)处理后Fig.3 The contour of Lung. (a)Before processing(b)After processing
寻找这些点集合通常有Graham扫描法以及Jarvis步进法。本研究运用的是Graham方法,其原理如图4所示。在平面上有若干点组成的集合,选取坐标最小的一个点,如图4(a)中的点1,将其余的点按照与点1构成的极角大小,从小到大进行排序并依次对点进行编号,如图4(a)所示。判断向量A与向量B的叉积,如果大于0,则点2是凸包上的点,反之则不是,如图4(a)中的点3。用直线连接所有凸包上的点,得到的最小多边形就是结果,如图4(b)所示。首先对图2(b)中的图像运用边界跟踪的方法得到图3(a)所示的轮廓,再运用上述方法得到图3(b)所示的结果。

图4 Graham算法原理。(a)处理前;(b)处理后Fig.4 The theory of Graham algorithm. (a)Before processing(b)After processing
1.3 边界逼近算法
边界逼近算法是本研究提出的核心算法,目的在于修正由于胸膜结节对肺实质轮廓所产生的凹陷,将病灶与肺实质一同分割出来,以便系统做进一步分析。将图3(b)进行区域填充后得到模板,如图5(a)所示;与原图像做乘运算后,得到如图5(b)所示的结果。该结果虽然将右肺边缘处的结节包含在肺实质内部一同被分割出来,但是在靠近心脏附近的肺凹陷处存在大量的过分割,这些非肺叶部分会对计算机辅助诊断系统的进一步处理和决策产生影响,因此需要运用算法来处理这一问题。

图5 过分割。(a)对图3(b)进行区域填充后得到的模板; (b)分割结果Fig.5 Oversegmentation (a)The mask which is the result of processing the Fig.3(b)by area filling(b)the result of segmentation
首先运用本文第1.2节中的Graham算法可以得到最小凸多边形端点的序列,如图6(a)中的点A和点B均是凸多边形上的端点。取点A与点B之间的肺实质轮廓线的中点C,计算C到AB的垂直距离CD,记为h,记AB间的欧式距离为W。根据h与W的值对凸多边形端点序列进行修正。修正方法如下:
1)当W>50时,将端点间轮廓线的中点C加入凸多边形端点序列,继续对AC做同样的判断。以此类推。
2)当40
3)当30 4)当W≤30且h<3时,同理。 运用上述方法对凸多边形所有的端点序列进行增补,对得到的端点序列用直线按顺时针方向相连。根据图1所示的流程处理后,得到图6(b)所示的结果。 1.4 实验方法 本研究的实验数据来自公开数据库LIDC中59位病人的CT样本图像,由于实验需要考量算法对于病灶的分割性能,故选取其中存在病灶的68张样本图像。样本大小均为512像素×512像素,实验环境为Windows 8.1、主频2.5 GHz、内存4 GB。开发平台VS2013、OPENCV2.4.9。 图7 分割结果比较。(a)第1幅原始图像;(b)阈值分割;(c)“滚球法”;(d)水平集方法;(e)本方法;(f)第2幅原始图像;(g)阈值分割;(h)“滚球法”;(i)水平集方法;(j)本方法Fig.7 Comparison of segmentation results. (a) The 1st original image; (b)Threshold segmentation; (c)“Rolling ball”; (d)Level set method; (e) Our proposed method; (f) The 2nd original image; (g)Threshold segmentation; (h)“Rolling ball”; (i)Level set method; (j) Our proposed method 在本文第2.1节中,将本算法与文献[2]中提出的“滚球法”、阈值分割法、水平集方法进行对比,根据医生诊断信息来判断病灶分割的正确与否。 阈值分割法仅运用OTSU算法二值化结合边界跟踪的方法,得到肺实质部分。 在文献[2]中,提出的“滚球法”的半径参数设定为最优的10[5]。 水平集方法的初始演化矩形设置:矩形的左上角坐标分别为(50,100)及(250,100),矩形宽190像素,高300像素,迭代总次数410次。 在本文第2.2节中,将对准确率、过分割比例、欠分割比例、算法执行时间做定量分析,并与公认文献中效果较好的算法做对比,说明本方法的有效性。其中,准确率的定义是以医生诊断结果为评判标准、正确地将病灶包含在肺实质内部分割出来的比例,过分割比例的定义是通过算法分割得到肺实质区域超出医生人工分割区域的面积占医生人工分割得到面积的比例,欠分割比的定义是医生人工分割得到肺实质区域超出算法分割得到区域面积占医生人工分割得到面积的比例。 2.1 方法对比 如图7所示,将本算法与文献[2]中提出的“滚球法”、阈值分割法、水平集方法进行对比,以医生诊断结果为评判标准,判断是否将胸膜结节连同肺实质正确地分割出来。图7(b)为普通的基于阈值分割的方法,将该结果与原图比较后可以看出,在自然生理弯曲的边缘处分割表现较好,但在右肺中叶边缘处未能将该胸膜结节一同分割出来,从而产生漏检。图7(c)是运用半径为10的滚球模型对图像处理的结果,可以看出分割出来的肺实质存在大量的过分割现象,破坏了肺实质内部的组织结构,因而影响到医生对肺内部的诊断。图7(d)是运用水平集方法得到的结果,可以看出右肺存在过分割且对于病灶的分割也不完整,这与初始轮廓位置以及迭代总次数相关。由于水平集方法[7]的主要思想是通过求解偏微分方程的方法使能量泛函最小化,从而使轮廓线演化至目标边缘达到分割的目的。增加迭代次数,可以使曲线演化最终停留在目标物体的边缘,从而解决欠分割问题,但同时也会造成胸膜结节的漏检。图7(e)是本算法结果,对于内轮廓上自然凹陷区域分割较好,同时也使外轮廓存在病灶的区域得到较好保留。图7(f)是第二组样本图像,医生的诊断信息是病灶位于右肺上叶尖端。图7(g)所示的阈值方法与图7(i)所示的水平集方法均未将病灶分割出来。图7(h)的滚球方法与本方法相比,病灶有一小部分缺失,且在其余位置有少许的过分割。图7(j)由本方法得到,其结果接近医生手动分割的结果。 2.2 量化评价 在本节中,将计算本方法分割结果的过分割比、欠分割比以及正确率。对样本集中68幅包含病灶的图像运用本算法进行处理,在表1中分别列举运用本算法及文献[6]的自适应边界匹配算法得到的过分割比例、欠分割比例。由于版面原因,仅列举误差较大的30组。通过实验得到,本算法对边缘结节分割的正确率为98.5%。将68组数据做算术平均后,得到本算法的平均过分割比例是1.35%,欠分割比例是0.51%。文献[6]所得到的平均过分割比例是2.73%,欠分割比例是0.85%。本算法运行68组图像所消耗的时间为5 506 ms,文献[6]所述方法的运行消耗时间为6 151 ms。由此可见,本方法在正确包含病灶进行分割的前提下,误分割的比例比文献[6]有明显降低,算法执行所消耗的时间略微缩短。 如表2所示,将本方法与公认的算法效果较好的文献[4-6]进行比较。文献[4]采用机器学习的方法,在406例实验中取得的平均欠分割比例略高于本方法与文献[6]的方法,正确率稍低于另两种方法。总体而言,机器学习的方法仍取得了很好的结果。不足之处在于需要对分类器进行训练,在算法执行时间上不如另两种方法,平均处理一张样本图像需要0.5 s[4],文献[6]方法和本方法的平均处理时间分别为0.09和0.08 s。文献[6]方法的稳定性较好,在对病灶分割的正确率上高于本方法,过分割与欠分割比例也略高于本方法。综合来看,本方法无需机器学习过程,在误分割的比例上取得较好的效果,在正确率方面接近于文献[6]。 表1 过分割比例及欠分割比例 表2 算法性能比较 运用图5与图7(e)得到的结果,分别做阈值化处理来分割肺内部所有的软组织,如图8所示。此对比意在说明运用传统分割法、滚球法所得到的结果存在过分割的干扰区域,或者是存在对胸膜结节漏检的情况,不利于计算机辅助诊断系统的进一步分析。由方法对比中的定性分析可见,本算法对病灶都有较好保留,同时又能抑制对非肺叶部分的过分割。如图8(a)所示,相比于过分割的情形,最大限度地减少自然生理弯曲所产生的过分割干扰区域,同时保留了胸膜结节,将它作为病灶的候选区域供计算机辅助诊断系统进行进一步检测。水平集方法与滚球法不同,前者需要设定初始演化区域位置,后者需要设置半径参数。本方法无需人工干预,可通过判定凹陷的宽度与深度之间的比例,自动对病灶位置进行修复。由实验中的量化评价可见,本算法在过分割与欠分割的比例上有明显的下降,同时又保证了一定的快速性,在对大量样本进行批量处理时,提高了计算机辅助诊断系统的执行时间与医生人工读片的效率。 图8 分割结果对比。(a)图7(e)结果; (b)图5结果Fig.8 Comparison of segmentation results (a) The result of Fig.7(e) (b)The result of Fig.5 本算法主要的问题是:对于如图9所示的样本,由于结节边缘不清晰,在预处理时将肺实质割裂成两块独立的连通域,从而使本算法并未将此二者作为一个整体区域来处理。如何判断此分裂位置是病灶、通过区域桥接的方法对分裂区域进行修正并通过算法将它分割出来,是今后着力深入研究的一个重点问题。 图9 错误的例子。(a)原图;(b)分割结果Fig.9 error example. (a) Original image (b)The result of segmentation 本研究主要讨论的问题是针对运用传统分割方法难以得到的胸膜结节,运用一种新方法来正确分割肺实质部分,从而使计算机辅助诊断系统能更好地做进一步的分析与决策;主要运用Graham算法得到最小凸多边形点的序列,再运用边界逼近的方法对凸多边形点的序列进行补正。针对自然弯曲的肺实质的内轮廓与外轮廓,通过判断凹陷最大深度与凹陷宽度的关系,区分自然凹陷与病灶点。本研究的下一步工作是运用机器学习的方法对分割出的胸膜结节、肺内部的血管等非病灶部分、孤立性肺结节做分类,完善计算机辅助诊断系统并进一步优化本方法,降低实验中出现错分的情形。 [1] Mansoor A, Bagci U, Foster B, et al. Segmentation and image analysis of abnormal lungs at CT: Current approaches, challenges, and future trends[J]. Radiographics, 2015, 35(4):1056-1076. [2] Samuel G Armato III, Maryellen L. Giger, computerized detection of pulmonary nodules on CT Scans[J]. Radio Graphics, 1999,19:1303-1311. [3] Guo PX, Guo H, Dai J. A Novel lung segmentation and boundary correction method[C]//Biomedical Engineering and Informatics. Tianjin: IEEE, 2009:1 - 4. [4] Shen S, Bui AAT, Cong J, et al. An automated lung segmentation approach using bidirectional chain codes to improve nodule detection accuracy[J]. Computers in Biology and Medicine, 2015,57:139-149. [5] 李金, 郑冰,梁洪,等.基于改进凸包算法的肺实质分割研究[J]. 中国生物医学工程学报, 2013, 32(4):484-490. [6] Pu J, Roos JC, Napel S, et al. Adaptive border marching algorithm: automatic lung segmentation on chest CT images[J]. Computerized Medical Imaging & Graphics, 2008, 32(6):452-462. [7] Chunming L, Chenyang X, Changfeng G, et al. Distance regularized level set evolution and its application to image segmentation.[J]. IEEE Transactions on Image Processing, 2010, 19(12):3243-3254. [8] Dai S, Lu K, Dong J, et al. A novel approach of lung segmentation on chest CT images using graph cuts[J]. Neurocomputing, 2015, 168:799-807. [9] Ju W, Xiang D, Zhang B, et al. Random walk and graph cut for co-segmentation of lung tumor on PET-CT images[J]. IEEE Transactions on Image Processing, 2015, 24(12):5854-5867. [10] Tasci E, Ugur A. Shape and texture based novel features for automated juxtapleural nodule detection in lung CTs [J].Journal of Medical Systems,2015, 39(5): 1-13. [11] Mohsen K, Zohreh A, Farshad T. Lung nodulesegmentation and recognition using SVM classifier and active contour modeling:A complete intelligent system[J].Computers in Biology and Medicine ,2013,43:287-300. [12] Sensakovic WF, Starkey A, Armato SG. A general method for the identification and repair of concavities in segmented medical images[J]. IEEE Nuclear Science Symposium Conference Record Nuclear Science Symposium. Dresden:IEEE,2008, 20(7):5320-5326. Lung CT Image Segmentation Based on Border Approximation Huang Zhiding1Sun Hong1,2,3* 1(SchoolofOptical-ElectricalandComputerEngineering,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)2(BusinessSchool,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)3(ShanghaiKeyLabofModernOpticalSystem,Shanghai200093,China) Segmentation of the lungs in chest-computed tomography (CT) image performs as an important preprocessing step in Computer-aided detection (CAD). The result brings a great effect for the further analysis and diagnosis. As the intensity of pleural nodule is close to the peripheral lung parenchyma, these lesions are not able to be segmented correctly using traditional method. The aim of this paper is to segment the lung including juxtapleural nodules in order to provide this focus for CAD system for the further analysis. This paper proposed a method that combined the Graham algorithm with border matching approximation to correct the contour of lung, and obtained the mask and multiply it by original image to segment lung image with juxtapleural nodules. Processing the 68 sample CT images including nodules from LIDC (Lung Image Database Consortium) through adopting new method proposed in this paper, and comparing this method with a traditional one, and analyzing the accuracy of this method and the rate of oversegmentation and undersegmentation, the accuracy of 98.5% , the oversegmentation rate of 1.35% and the undersegmentation of 0.51% were determined, which proved the effectiveness of this method. lung segmentation; lung nodule; computer-aided detection 10.3969/j.issn.0258-8021. 2016. 05.001 2016-02-19, 录用日期:2016-06-27 国家自然科学基金(61170277, 61472256);上海市教委科研创新重点项目(12zz137); 沪江基金(C14002) R318 A 0258-8021(2016) 05-0513-06 *通信作者(Corresponding author), E-mail: 823372873@qq.com
2 结果
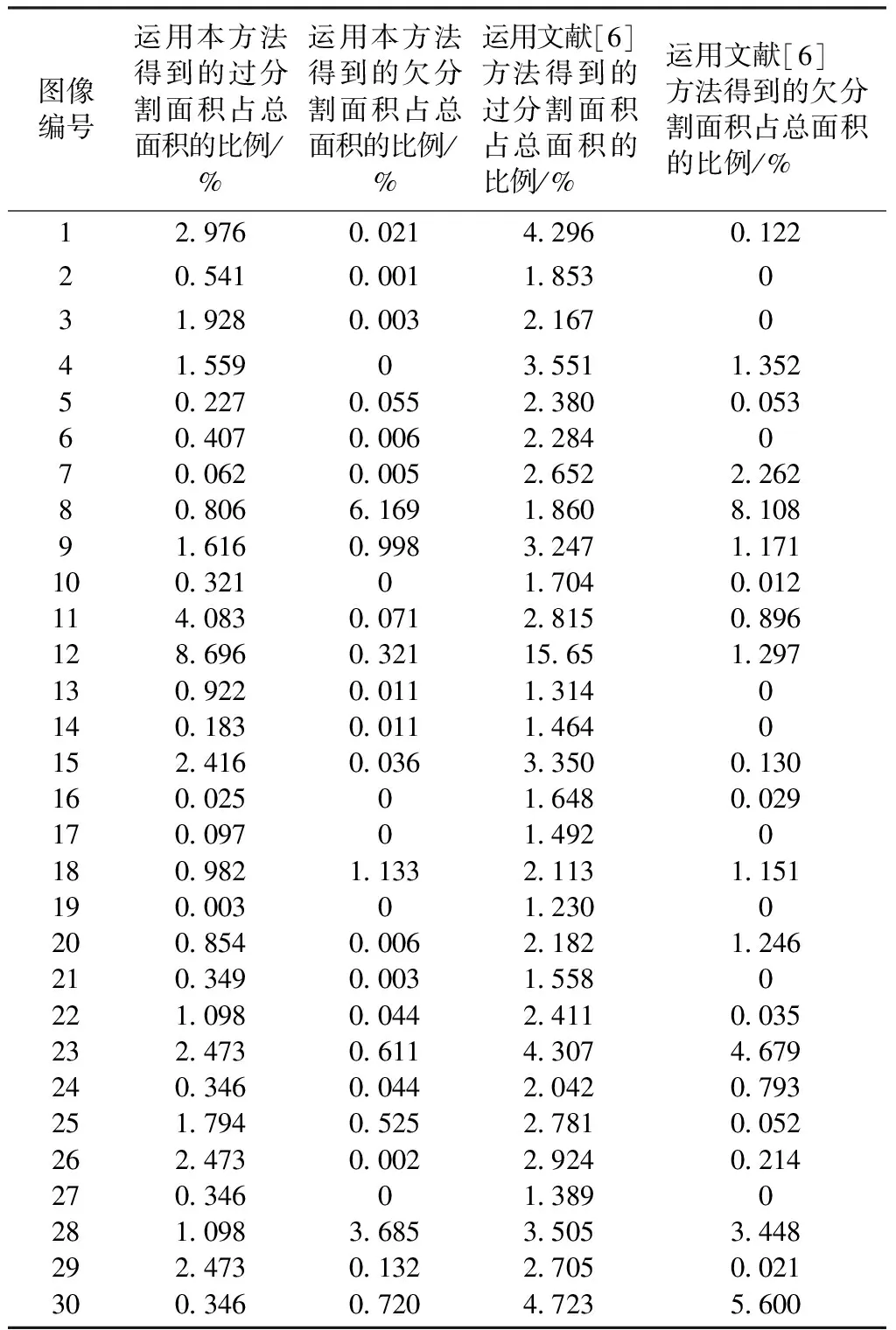
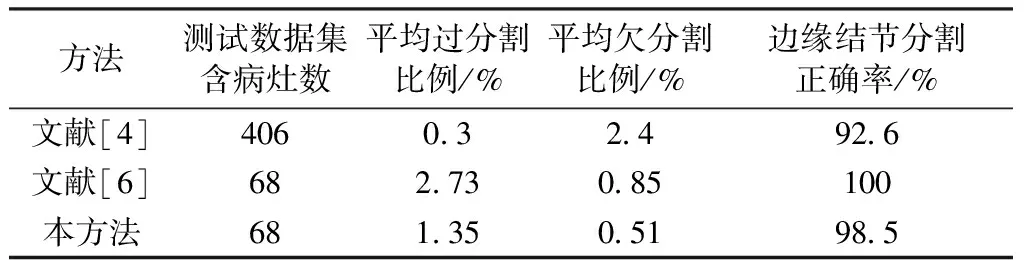
3 讨论和结论


