基于Shapley值理论的能源系统需求预测方法

李娜，刘树勇，曾鸣，刘丽霞，李源非，韩旭

(1. 国网天津市电力公司经济技术研究院，天津市 300000； 2. 华北电力大学经济与管理学院，北京市 102206)

基于Shapley值理论的能源系统需求预测方法

李娜1，刘树勇1，曾鸣2，刘丽霞1，李源非2，韩旭2

(1. 国网天津市电力公司经济技术研究院，天津市 300000； 2. 华北电力大学经济与管理学院，北京市 102206)

合理而准确的能源消费预测对于科学制定能源规划、优化调整能源与产业结构具有重要意义。针对传统能源预测方法预测精度低、未充分计及环境政策影响的缺点，提出了基于Shapley值理论的多情景修正组合预测模型。首先，根据能耗预测的要求和特点选取3个单项预测模型，并通过博弈论Shapley值理论确定单项模型在组合模型中的权重从而得到基准预测结果；然后，量化技术进步、经济发展、政策变动3个环节为修正项和修正系数，进一步改进模型函数，得到不同情景下的修正预测结果；最后，基于T市生活能耗数据进行算例分析，结果表明所提方法能够实现预测值曲线与实际值曲线的高度拟合，在充分考虑环境政策影响的基础上提高能源预测精度，为有关部门进行能源规划提供决策依据。

组合模型；能源消费预测；Shapley值；情景修正

0 引 言

近年来随着我国经济的快速发展和现代化建设的持续推进，我国的能源供应和能源消费正面临能源产供不平衡与能源结构不合理两大矛盾。从能源和产业规划的角度入手，进行合理而准确的能源消费预测将是深化能源革命与可持续发展战略、缓解两大矛盾的关键。2015年既是我国“十二五”的收关年，又是“十三五”的布局年，在这一关键的时间点，分析不同环境、政策及规划对能源消费情况的量化影响，对我国未来的能源消耗进行科学预测具有重要的现实意义。

在能源消耗预测领域，中外学者和研究团队开展了大量的研究，这些研究主要集中在理论分析和建模计算2个方面。在理论分析方面，文献[1]分析了影响中国能耗强度的各种因素，并剖析了我国实现节能减排的主要工作突破点；文献[2]梳理了改革开放以来我国在能源领域的政策，归纳出我国能源供需的特征，粗略预测了未来我国能源的增长情况，最后给出了完善中国能源治理模式的建议；文献[3]通过历史数据的横纵向比较，说明了浙江省终端能源市场结构演化的特征，并运用二次规划法对未来的发展方向进行预测；文献[4]综述了国内外的能源预测模型和安全评价体系，并梳理了常见研究成果的长处和不足；文献[5]收集了世界两大能源预测机构近年的预测数据，并进行误差精度分析，在此基础上建模分析预测模型设定值对能源需求预测误差的影响。在建模计算层面，中外学者和研究团队运用了多种模型进行了各种形式的能耗预测。文献[6-7]基于马尔科夫链分别建立北京市终端能源预测模型和全国能源结构与污染、排放量预测模型；文献[8]提出了改进的GM(1，1)-LSSVM模型，并用辽宁省的历史数据检验了模型的有效性；文献[9]建立了系统动力学模型，研究政府调控政策对能源供需的影响；文献[10-13]分别运用GA-SA模型、LMDI分解法、粒子群优化算法和ARIMA模型对我国能源消费总量进行预测；文献[14-16]建立多种组合模型对辽宁、天津等地的能耗进行预测，结果显示根据预测要求选择各类模型进行组合，可以保证良好的精度；文献[17]从电能替代的角度入手，建立电能替代效果评价模型，并给出电能替代对能源结构影响的量化分析。文献[18]综合运用组合模型和情景分析法对云南省的能耗进行预测，但在情景分析环节中该文献给出的情景预测值以直观的判断为主，缺少定量分析。

纵观中外学者和团队的研究成果，大多都是根据历史数据直接运用数值计算方法做出预测，极少数进一步建立主观划分的不同情景，预测结果的准确性难以考证。基于此，将博弈论Shapley值理论引入，提出一种组合模型权重计算方法，并获得能耗预测基准值；然后，在修正环节中考虑环境政策的量化影响，将技术进步、经济发展、政策变动等定量反映到预测结果中，对基准预测结果进行修正，提升模型预测精度和现实意义；最后，通过T市生活能耗算例，分析验证提出模型的科学性和合理性。

1 基于Shapley值理论的组合预测模型

本节将建立能耗预测组合模型。通过该模型计算，可得到各行业的能源消费结构和生产总值预测结果。在整体的预测过程中，本节组合模型的计算结果作为待修正的基准情景，即技术进步、经济发展、政策变动等环节维持原有的发展趋势，不发生重大变化的预测结果。

1.1 组合预测和Shapley值理论的基本原理

不同的单项预测方法各有优缺点，他们分别从各自的角度对研究对象进行了深度的信息挖掘，倘若只采用1种预测方法就可能会造成部分有用信息丢失。无论预测精度大还是小，各个单项预测中都包含系统独立的信息，如果只考虑某一个模型则会造成信息的浪费，而如果将不同的预测方法组合起来则会增加系统的预测性能。因此，基准情景的预测采用加权平均组合预测的基本思想，再进一步对预测结果取加权平均得到最终的预测值。根据能源预测的基本特性和模型的具体应用要求，为兼顾组合模型的准确性和计算效率，选择3种模型进行组合，进一步应用博弈论中的Shapley值理论确定各预测方法在最终预测值中的权重，如式(1)所示：

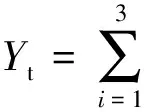
(1)

式中：Yt为基准情景预测值；Yit为第i种模型的预测值；i是第i种模型的权重。

第i种模型预测误差绝对值的平均值为

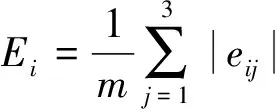
(2)

式中：m为具体样本的数目；eij为第i种预测模型下第j个数据的残差。

总的平均预测误差为单个模型预测误差绝对值的平均值，如式(3)所示：

(3)

引入博弈论中的Shapley理论，将单个预测模型产生的误差看作是该模型的收益，则组合预测模型的总误差就被看作是各个预测模型的共同受益，因此各模型事实上构成了一种合作关系。根据Shapley值理论把组合预测总误差看作总收益分配到单个预测模型中，这样就确定了组合预测模型中单个预测模型的权重。Shapley值误差分配公式为

(4)

其中：

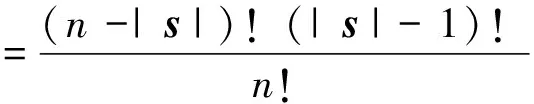
(5)

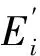
(6)

1.2 单项模型的选择

(1)一元线性回归模型。

一元线性回归模型在多种预测方法中适应性最广，且在不同类型的预测中的误差水平差异不大，其预测结果比较适合作为基础值的一部分。另外，一元线性回归模型在历史数据充分的时候具有良好的性能，而本次能耗预测中可以通过统计年鉴得到近15年的数据，较为可观。故选择一元线性回归模型作为组合预测模型中的模型之一。

(2)灰色预测GM(1,1)模型。

灰色预测法适用于外部环境既有已知因素，又有未知因素情况时的预测，适用于呈指数分布的时间序列数据。在多种灰色预测模型中，灰色GM(1，1)预测模型是灰色预测法中应用最为广泛的一种模型，进行能源需求预测具有较好的效果，是一种指数增长型模型，具有需要样本量少、预测精度较高的特性[19]。综上分析，选择灰色GM(1,1)模型作为组合预测模型中的模型之一。

(3)二次指数平滑模型。

指数平滑法是在移动平均的基础上通过计算指数的平滑值来构建预测模型的。其基本思想是根据观测值的历史数据的加权和得到预测值，其中权重的确定与数据的时间有关，新数据权重大，旧数据权重小，从而兼容了各种时期的数据，适用于能耗预测的原始数据形式。根据适用的数据序列不同，指数平滑法可以划分为一次指数平滑、二次指数平滑和三次指数平滑。其中，二次指数平滑在能耗预测的应用中最为广泛。因此，选择二次指数平滑模型作为组合预测模型中的模型之一[20]。

2 基于多种政策与经济发展环节的多情景修正方法

在基准情景预测中，得到技术、经济和政策因素沿原有趋势发展下的生产总值和能耗值预测值。记第A种行业的生产总值预测值为Yt,A；记第i种行业第A种终端能源消耗的预测值为Ct,A,α。其中，A∈{所有行业}；α∈{所有终端能源}。需要指出，由于三次产业和生活能耗考虑的终端能源种类不同，且二者的变化互相影响程度不大，故将三次产业和生活能耗分开进行计算和预测。在进行多情景预测时，主要考虑技术进步、经济发展和政策变动三大环节[20]。

2.1 技术进步环节

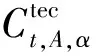
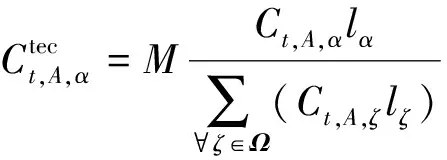
(7)

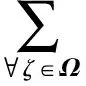
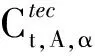
2.2 经济发展环节

经济发展环节将会影响生产总值，并成比例地影响能耗。在基础情景的预测中，实际上已经包含了经济平稳发展这一趋势。因此在经济发展环节的修正中，强调的是经济高于或低于经济平稳发展的部分对于能耗的影响，该影响具体以经济发展修正系数表现。考虑到之后需要根据行业调整政策对每一个行业的生产总值进行具体的修正，为避免冗余，这里只对宏观经济的发展进行整体的调整，并假设宏观经济的发展是由每一个行业的平均发展共同带动的，如式(8)所示：

(8)

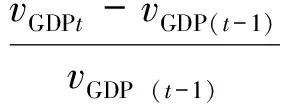
2.3 政策变动环节

会对终端能源消耗产生明显影响的政策变动在预测三次产业能耗时主要有3方面，即能源结构调整(电能替代的情况较为特殊，需要单独测算)、产业结构调整和节能减排政策。在预测生活能耗时不考虑产业结构，但是需要考虑人口因素。关于人口因素的考虑将在最后说明。

(1)能源结构调整(不包括电能替代)。

能源结构调整即在能耗总量不变的情况下通过经济、行政手段调整各种终端能源消耗的比例。根据常见的能源结构调整政策和方案中的表述方式，能源结构调整主要是要求“α能源占终端能源消耗的N%”。其本质是将多用或少用的某种能源用其他能源来填补替代。这是一种直接的增减关系，故以修正项的形式来表达。

首先根据式(9)判断终端能源α是需要被替代的能源还是需要替代其他终端能源的终端能源。

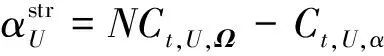
(9)

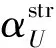
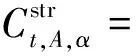
(10)

(2)电能替代。

参考常见的电能替代政策的表达方式，电能替代通常要求“在A产业实现电能X替代(比如，在生活用能中实现电能11亿kW·h替代)”。其本质是在某一产业中用电能替代其余终端能源。电能替代的特殊性主要有2个方面。第一，由于考虑的终端能源种类不同，电能替代应将三次产业和生活能耗分开进行测算。第二，不论在何种行业进行电能替代，在降低本行业其余终端能源消耗的同时，都将会增加电力行业的能耗。

电能替代的影响也是以修正项的形式反映的，对电能的修正项如式(11)所示：

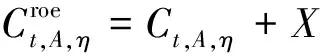
(11)

式中：η代表电能；X表示需要输入的电能替代的量。

对A产业中其他终端能源的修正，基本思路也是将电能折标后的能耗按比例分配。修正项如式(12)所示：

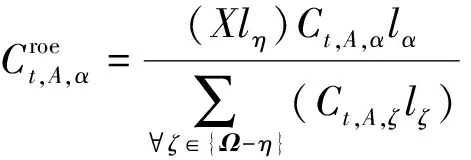
(12)

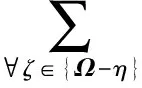
现考虑电能替代对火力发电的影响。各地的电能既有自发的，又有外购的。参考各地统计年鉴中的电能平衡表，自发电占总电能生产量的比例不固定且不表现出明显的统计特性，难以进行统计学层面的预测，加之各地可能对这一比例的大小存在政策上的要求，因此这个比例宜作为预测的条件来输入，记为λ。假设用于替代的电量X按这一比例从属于自发电和外购电，则只有自发电的部分将会影响能耗。参考国内平均水平、相关文献和政策，取火力发电厂供电煤耗为310 g/(kW·h),则电能替代将会造成电力的生产和供应业增加煤耗(修正项)为

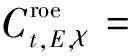
(13)

式中：E和分别表示电力的生产和供应业和终端能源煤的下标。

(3)产业结构调整。

产业结构调整将会通过生产总值的变化来影响能耗。参考相关政策，产业结构调整主要是要求“A产业生产总值占全行业生产总值的L%”。在此基础上，生产总值的扩张或紧缩将会成比例地改变能耗，故产业结构调整反应为修正项的形式，如式(14)所示：

(14)

式中：ρind表示产业结构修正系数；L为需要输入的调整后的产业A占所有行业的比重。

(4)节能减排政策。

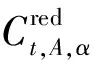
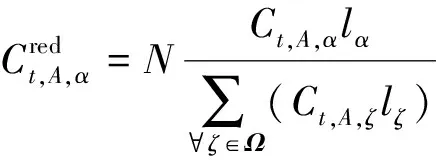
(15)

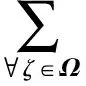
(5)人口增长环节。

人口增长的预测需要专门的计算方法和工具，该部分的内容并不是研究的重点。因此对于人口增长环节的考虑是：对于具体地区的人口增长预测，引用其他文献成果作为参考。而根据文献调研，许多参考文献当中都包含有不同人口政策强度下人口增长的多情景预测结果。

2.4 多情景修正结果

(16)

再将同种终端能源在各分行业中的消耗量进行加总，即可得到该终端能源的总消耗，如式(17)所示：

(17)

3 算例分析

为了验证提出模型的科学性和合理性，本节将以T市生活能耗作为算例进行分析。算例分为2部分，首先，根据1996—2010年已知数据，参考《T市“十二五”规划纲要》进行情景修正，预测得出2011—2013年能耗数值，并将修正结果同实际结果进行误差校核；然后，在确保模型科学合理的基础上，进一步对2016—2020年T市生活能耗进行预测，得出T市“十三五”时期的生活能源消费结构。

3.1 历史数据

根据《T市2014年统计年鉴》，1996—2013年T市生活能耗和人口情况见表1。

2009年T市自发电量占可供电量的72.92%。另外根据参考文献，3种人口政策情景下的人口预测见表2[21]。

3.2 2011—2013年能耗预测及校核

根据《T市“十二五”规划》、《T市节能“十二五”规划》、《T市新能源新材料产业发展“十二五”规划》、《T市环境保护“十二五”规划》、《T市某新区能源发展“十二五”规划》等文件。在生活能耗方面，需要输入的情景变量主要有以下几项：

表1 T市生活能耗和人口情况(1996—2013年)

Table 1 Daily life energy consumption and population of T city (1996-2013)

表2 T市人口情景预测(2011—2013) 万人

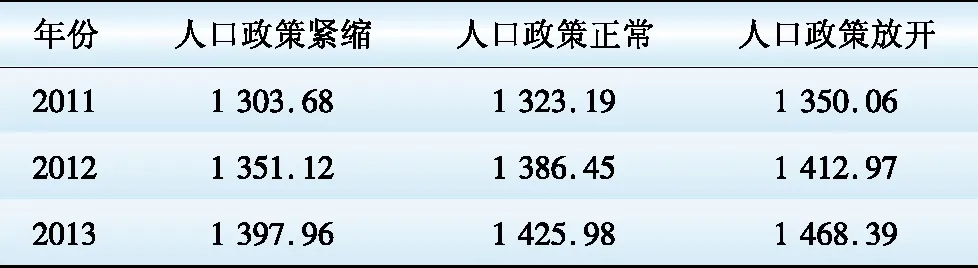
(1)到2015年，在一次能源中，煤炭比例在60%以下，天然气比例在8%以上，清洁能源比例在3%以上；

(2)到2015年，建立完善的节能服务体系和节能服务市场，实现年节约量50万t标准煤;

(3)到2015年，通过实施节能技术推广工程，实现年节电10亿kW·h;

(4)到2015年，T市从区外受电超过300万kW，比例约为30%;

(5)由于放开单独二孩等人口政策，认为“十二五”期间T市人口生育政策倾向于放开。

上述变量以比例分摊的总体思路分摊至各产业和生活能耗当中，在模型中进行输入。另外，由于预测只进行到2013年，因此把到2015年实现的节能目标按年份均摊到各年，得到各年的修正变量情况。

(1)基准情景预测结果。

将基本参数输入模型中进行计算，取人口政策为正常强度，得到2011—2013年T市生活能耗和人口基准情景预测结果如表3所示。

表3 T市生活能耗和人口情况基准情景预测

Table 3 Daily life energy consumption and population forecasting of T city

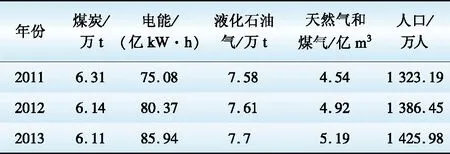
(2)基准情景预测结果。

将情景修正输入量代入修正环节的函数中，对基准情景预测结果进行多情景修正。得到模型预测结果，即2011—2013年T市生活能耗和人口的预测结果如表4所示。

表4 T市生活能耗和人口情况预测修正结果

Table 4 Daily life energy consumption and population forecasting of T city after correction

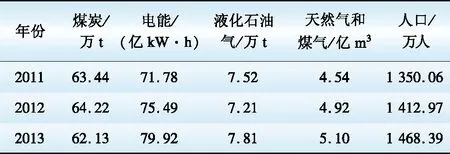
将经过修正的4种终端能源和基准情景的结果绘制在同一直角坐标系中，如图1—4所示。

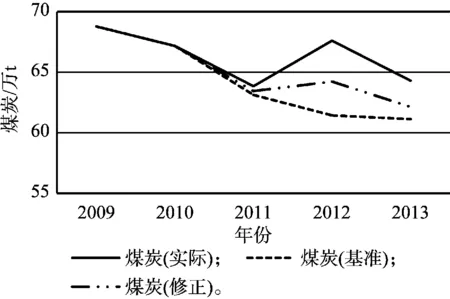
图1 煤炭消耗预测与实际结果

由图1—4可以看出，修正环节起到了减小误差的作用。具体的误差分析将在下面进行。

(3)误差校验分析。

将以上预测结果对比2011—2013年T市生活能耗的实际值，计算得到各年预测值的误差率和平均误

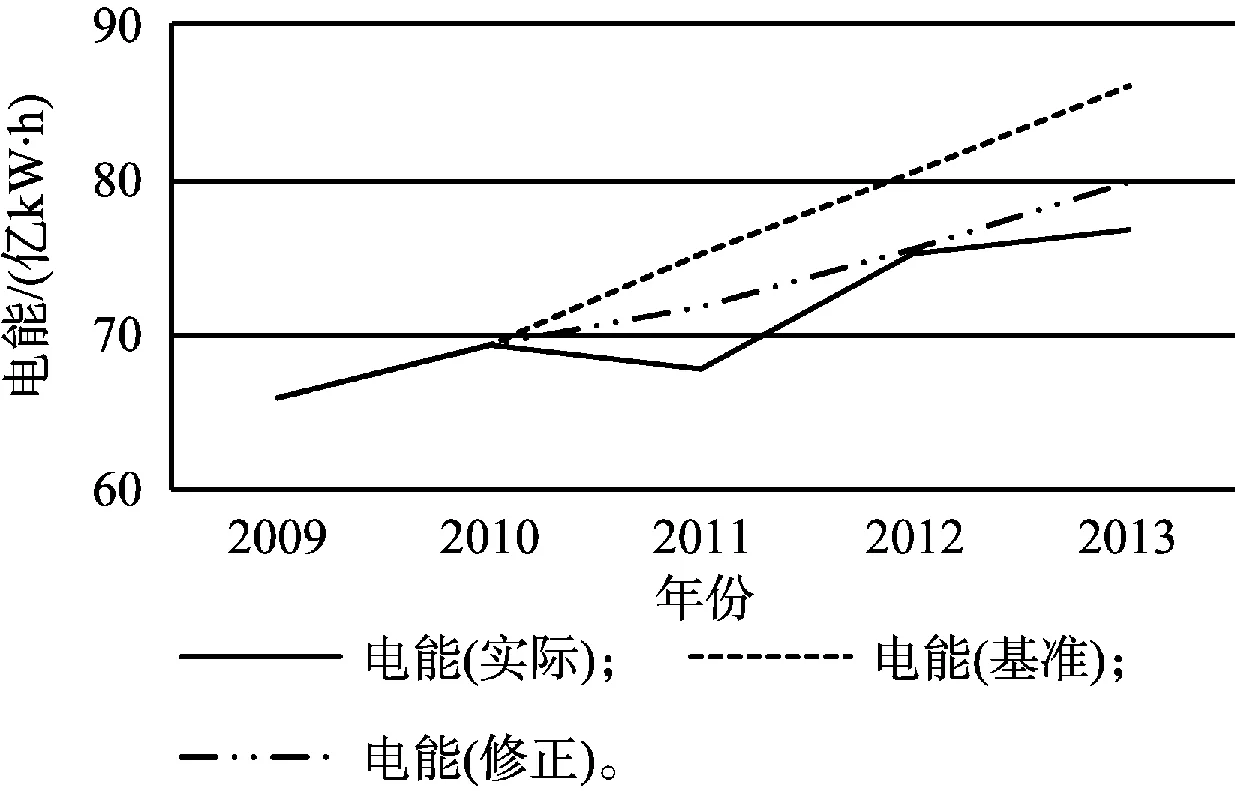
图2 电能消耗预测与实际结果

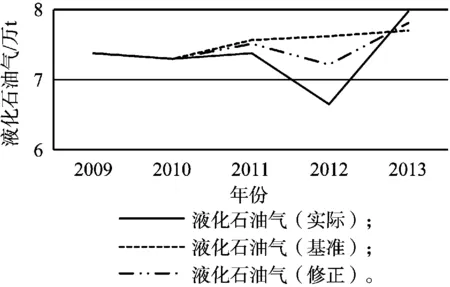
图3 液化石油气消耗预测与实际结果

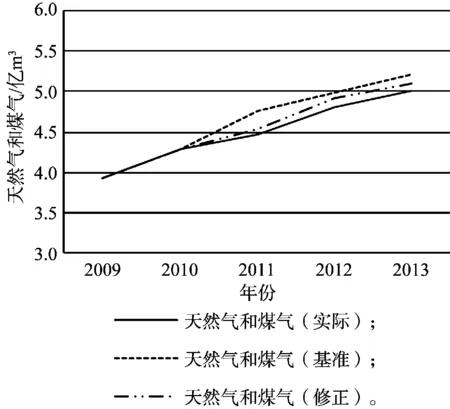
图4 天然气和煤气消耗预测与实际结果

差率，总结如表5所示。

选择的参考文献对T市人口的预测误差很小，可以忽略人口误差对预测结果的影响。由以上图表可以看出，根据提出的修正预测模型，修正值曲线与实际值曲线的拟合程度较基准值更优，更符合数值变化趋向；4类终端能源消耗预测误差都在5%以内，符合能源消耗综合预测的要求且精度较高。

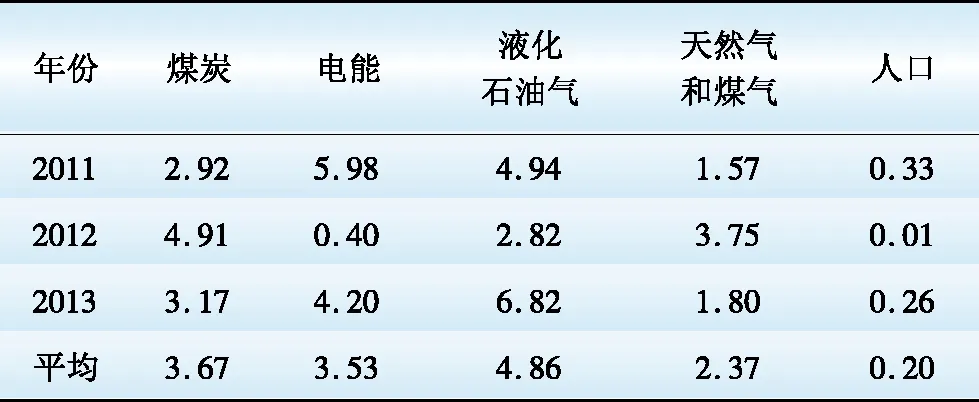
表5 T市生活能耗和人口情况预测误差表(2011—2013年)

Table 5 Errors of daily life energy consumption and population forecasting of T city (2011-2013) %

3.3 “十三五”时期生活能耗预测

本节以1995—2013年的全部数据为基础，预测T市“十三五”时期的生活能耗情况。假设所有“十二五”期间的情景修正继续沿用至“十三五”规划中。预测结果如表6所示。

表6 “十三五”时期T市生活能耗预测结果

Table 6 Daily life energy consumption forecasting results of T city during “The Thirteenth Five-Year-Plan”

2020年相较于2015年的生活能耗增长率见表7。

表7 T市2020年生活能耗相较2015年的增长率 %

Table 7 Growth rate of daily life energy consumption of T city in 2020 compared with that in 2015

根据国家能源局给出的能源折标系数将4类终端能源折算成标准煤，得到2020年T市的生活能源结构如图5所示。

由上述预测结果可知，“十三五”时期，T市生活终端能耗结构将逐步调整。一方面，煤炭消耗维持低增速，而包括电力、天然气在内的国家推广清洁能源获得较好的增速；另一方面，电能将成为T市主要生活终端能源，电能替代政策推进了能源结构优化。

图5 2020年T市能源结构图

4 结 论

提出了基于Shapley值理论的多情景修正组合预测模型，该模型能够综合考虑技术进步、经济发展、政策变动等环节变化对能耗预测的影响，并定量地反映到能耗预测的结果中。通过对T市生活能耗预测的算例分析，证明了所提模型在中短期预测中具有较高的精确度，在进一步修正预测结果后，与实际值的拟合度更优。研究成果和结论具有科学性和合理性，可为有关部门进行能源规划与决策时提供一定的参考依据。

[1]王祥. 中国能耗强度影响因素分析与节能目标实现[D]. 沈阳：东北财经大学, 2012. WANG Xiang. The research for influencing factors of China energy consumption intensity and achieve of target to saving energy[D]. Shenyang：Dongbei University of Finance and Economics, 2012.

[2]邬亮, 赵小凡, 齐晔. 改革开放以来中国能源供需特征与治理模式[J]. 中国人口资源与环境, 2014(12): 147-152. WU Liang, ZHAO Xiaofan, QI Ye. Demand, supply and governance of energy in reform-era China[J]. China Population Resources and Environment, 2014(12): 147-152.

[3]王刚, 徐园, 叶承晋. 浙江省终端能源结构演化进程分析[J]. 能源工程, 2015(1): 26-30, 36. WANG Gang, XU Yuan, YE Chengjin. Analysis of the terminal energy structure evolution process in Zhejiang province[J]. Energy Engineering, 2015(1): 26-30, 36.

[4]付立东, 张金锁, 冯雪. GA-SA模型预测中国能源需求[J]. 系统工程理论与实践, 2015,35(3):780-789. FU Lidong, ZHANG Jinsuo, FENG Xue. GA-SA model forecasting China’s energy demand[J].Systems Engineering-Theory & Practice,2015,35(3):780-789.

[5]陶然, 蔡云泽, 楼振飞, 等. 国内外能源预测模型和能源安全评价体系研究综述[J]. 上海节能, 2012(1):16-21. TAO Ran, CAI Yunze, LOU Zhenfei, et al. Comprehensive research of domestic and foreign energy forecast model and energy safety appraisal systems [J].Shanghai Energy Conservation, 2012(1):16-21.

[6]韩睿. 能源需求预测误差成因研究及启示——基于IEA和EIA中长期预测数据[D]. 北京：北京理工大学, 2015. HAN Rui. Study on energy demand medium-and long forecast error causes of world major energy agencies——IEA&EIA[D]. Beijing：Beijing Institute of Technology, 2015.

[7]张旭超. 北京市终端能源预测模型及发展对策研究[D]. 北京：华北电力大学, 2009. ZHANG Xuchao. Research on end-use energy forecasting model and strategy of sustainable development in Beijing[D]. Beijing：North China Electric Power University, 2009.

[8]刘殿海, 杨勇平, 杨昆, 等. 基于马尔科夫链的能源结构与污染物排放预测模型及其应用[J]. 中国电力,2006,39(3):8-13 LIU Dianhai, YANG Yongping, YANG Kun, et al. Forecasting model and its application of energy structure and pollutant emission based on Markov chain[J].Electric Power,2006,39(3):8-13.

[9]叶彬, 秦丹丹, 杨欣, 等. 电力占终端能源消费比重分析预测方法及应用[J]. 电力与能源, 2014(2): 156-161. YE Bin, QIN Dandan,YANG Xin, et al. Analysis & forecasting method and application of electric energy proportion in final energy consumption[J].Power & Energy,2014(2):156-161.

[10]柴岩, 刘翔. 改进的GM(1,1)-LSSVM模型及其在能源消耗预测中的应用[J]. 统计与决策, 2014(17): 84-87.

[11]王明刚, 廖为鲲,许华, 等. 政府调控下的能源供需系统动力学分析[J]. 数学的实践与认识,2013,43(8) : 50-61. WANG Minggang, LIAO Weikun, XU Hua, et al. Energy demand-supply model with government regulation and its dynamical analysis[J].Mathematics in Practice and Theory,2013,43(8) : 50-61.

[12]陈卫东, 朱红杰. 基于粒子群优化算法的中国能源需求预测[J]. 中国人口资源与环境, 2013(3): 39-43. CHEN Weidong, ZHU Hongjie. Energy demand forecast in China based on particle swarm optimization algorithm[J]. China Population Resources and Environment, 2013(3): 39-43.

[13]秦国真. 云南能源需求影响因素分析及预测[D]. 昆明：云南财经大学, 2012. QIN Guozhen. Energy demand impact factors analysis and forecasts of Yunnan province[D]. Kunming：Yunnan University of Finance and Economics, 2012.

[14]张志启. 我国能源消费总量预测建模分析[D].包头：内蒙古科技大学, 2012. ZHANG Zhiqi. Modeling analysis of China’s total energy consumption predictive[D].Baotou：Inner Mongolia University of Science and Technology, 2012. [15]谭显东, 胡兆光, 彭谦. 考虑能效电厂的供需资源组合优化模型[J]. 电网技术,2009, 33(20):108-112. TAN Xiandong, HU Zhaoguang, PENG Qian. A resource combination optimization model considering efficiency power plant[J]. Power System Technology, 2009, 33(20):108-112.

[16]陈玉金, 刘建永, 李凌, 等. 基于神经网络回归分析组合模型的能源消耗预测研究[J]. 兵工自动化,2008,27(11): 59-60. CHEN Yujin, LIU Jianyong, LI Ling, et al. Forecast and research on energy consumption based on analytical and combined model of BP neural network and regression[J].Ordnance Industry Automation,2008,27(11): 59-60.

[17]尹航. 节能减排环境下电能替代其他能源评价方法研究[D]. 北京：华北电力大学, 2013. YIN Hang. Energy conservation and emission reduction environment power to substitute other energy evaluation method research[D]. Beijing：North China Electric Power University, 2013.

[18]万磊, 郑季良. 基于情景分析法的云南省能源消耗预测[C]//第三届(2008)中国管理学年会——金融分会场论文集. 长沙：中国管理现代化研究会, 2008: 5.

[19]KUMAR U, JAIN V K. Time series models (grey-markov, grey model with rolling mechanism and singular spectrum analysis) to forecast energy consumption in India[J]. Energy, 2010, 35(4): 354-362[20]JUNGHANS A . Decision support model for energy-efficient improvement of entire building stocks [J]. Facilities, 2013, 31(3): 173-184. [21]王舒容. 天津市人口发展趋势预测[D]. 天津： 天津理工大学, 2013. WANG Shurong. Prediction of the trend of population development in Tianjin[D]. Tianjin：Tianjin University of Technology, 2013.

(编辑 张媛媛)

Energy Demand Forecasting Method Based on Shapley Value Theory

LI Na1, LIU Shuyong1, ZENG Ming2, LIU Lixia1, LI Yuanfei2, HAN Xu2

(1. State Grid Tianjin Economic Research Institute, Tianjin 300000, China; 2. School of Economics and Management, North China Electric Power University, Beijing 102206, China)

The reasonable and accurate prediction of energy consumption is of great significance for scientifically making energy plan and optimizing the structure of energy and industry. Aiming at the shortcomings of the traditional energy forecasting method, which has low prediction accuracy and not be fully accounted for the influence of environmental policies, this paper presents a combined forecasting and scene correction model based on the Shapley value theory. Firstly, according to the requirements and characteristics of energy consumption forecasting, we select three single forecasting models, and determine the weight of the single model in the combined model through the Shapley value theory to obtain the basic forecasting result. Then, three main aspects of technological progress, economic development and policy change are quantified as the correction term and coefficient to further improve the model function and obtain the modified prediction results under different scenes. Finally, the case of life energy consumption in T City is studied. The results show that the forecasted value curve and actual value curve are highly fitted in the proposed method, which can improve the accuracy of energy forecasting based on the full consideration of environmental policy influence and provide decision basis for the energy planning of related departments.

combined model; energy consumption forecasting; Shapley value; scene correlation

F 206； F407.61

A

1000-7229(2016)01-0015-08

10.3969/j.issn.1000-7229.2016.01.003

2015-10-12

刘树勇(1978)，男，硕士，高级工程师，主要从事电力市场分析预测工作；

李娜(1985)，女，博士，中级经济师，主要从事能源电力经济研究工作；

曾鸣(1957)，男，教授，博士生导师，研究方向为电力技术经济及需求侧响应；

刘丽霞(1981)，女，硕士，高级工程师，主要从事能源与电力市场分析工作；

李源非(1993)，男，硕士，研究方向为电力市场理论与应用；

韩旭(1990)，女，博士，研究方向为电力经济管理。