动静压信号误差对飞控系统影响分析及处理方法

张欢，邹俊俊，饶明波，曾行，黄勇强，杨振声

（中航工业洪都，江西南昌330024）

动静压信号误差对飞控系统影响分析及处理方法

张欢，邹俊俊，饶明波，曾行，黄勇强，杨振声

（中航工业洪都，江西南昌330024）

某飞机多功能探头的动静压信号未经校准，存在较大误差。本文结合余度管理逻辑对飞控系统所用信号的误差进行确认后，再进行系统纵向阻尼比、操纵期望参数、稳定储备及时域响应特性的仿真分析，明确了误差对飞行品质及稳定储备的影响，并提出了解决方法。

飞控系统；动静压信号；误差分析

0 引言

在飞控系统设计中，为获取良好的系统性能和飞行品质，对系统参数的调节必不可少[1]。飞控系统控制律参数是随动压和静压进行调节的，如果动压和静压误差较大，控制律解算过程中用到的参数就会有较大差别，这将对系统的性能和飞行品质产生影响，甚至会影响到飞行安全。由此可见，动静压信号的精度对于飞控系统至关重要。

动静压信号的精度取决于大气数据传感器的精度。大气数据传感器把飞机空速管系统测得的总压和静压转换成电信号形式的动压和静压发送给飞控计算机。

某飞机之前安装有机头空速管、L形空速管及多功能探头（带空速管），且前两者都已经过校准，解算出的动静压信号引入了飞控系统用于控制律调参；后者尚未校准，精度尚不满足要求，飞控系统未使用。现需安装机头雷达，取消机头空速管，而将多功能探头动静压信号用于飞控系统调参。为确定对飞控系统的影响，确保系统性能和飞行品质满足要求，需进行误差影响分析。

本文首先对多功能探头误差范围进行确认，并结合余度管理逻辑对飞控系统动静压信号表决值误差进行分析；再通过对系统纵向阻尼比、操纵期望参数、稳定储备及时域响应特性的仿真分析，得出误差的影响；最后提出处理方法，并对其进行任务可靠性计算，解决了动静压误差较大的问题，同时保证了系统可靠性。

1 动静压信号误差

飞控系统动静压信号出现误差的源头是大气数据传感器测量误差，此误差范围通常由试飞数据进行确认。各传感器解算的动静压信号经过余度管理监控表决后，得出飞控系统动静压表决值，用于控制律解算。由此可见，传感器测量误差最终将影响动静压表决值。

1.1 试飞数据

某飞机L形空速管和多功能探头均配置两个，左右对称分布于机头两侧，每个传感器各提供一路动、静压。为进行误差分析，截取某飞机以往试飞数据中的机头空速管、L形空速管及多功能探头的总、静压信号曲线分别如图1、图2所示。

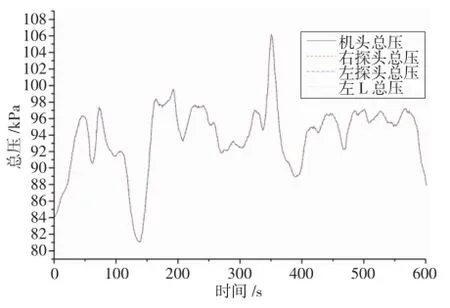
图1 各传感器总压比较

图2 各传感器静压比较

从试飞数据可以看出：多功能探头与机头空速管、L形空速管的总压一致性较好，可认为精度满足要求；多功能探头比机头空速管、L形空速管静压值小，差异最大时接近8kPa；同时还存在较大正向跳变，最大幅值接近8kPa。

由于机头空速管和L形空速管已经过校准，精度满足要求，因此，可认为多功能探头总压接近真实值，而动压比真实值小，在差异最大时小8kPa。

1.2 表决值误差

为分析多功能探头信号误差对飞控系统的影响，需明确动静压信号的使用方式。

在采集多余度信号进行输出时，为得出安全的输出信号，飞控系统将对信号进行余度管理监控和表决[2]。某飞机飞控系统对动、静压信号表决逻辑为：将四余度信号按大小排序，求出它们之间的差值，若差值小于监控门限(静压为8kPa)则信号有效，大于则在经过相应的监控时延后判为无效：

1）四余度均有效时，取中间两值的平均值；

2）三余度有效时，取中间值；

3）两余度有效时，取两值的平均值；

4）单余度有效时，取该值；

5）2：2或1：1：1：1时，取中间两值的平均值。

从试飞数据可以看出，多功能探头静压值偏小，差异最大时小8kPa，未超过静压监控门限，根据飞控系统余度管理逻辑，静压表决值与L形压力受感器静压的中值，即误差最大时较真实静压小4kPa；而多功能探头总压接近真实值，减去静压后为动压，即此时动压大4kPa。

2 误差影响分析

在明确动静压最大误差后，通过对飞行品质及稳定裕度进行仿真计算，分析其对飞控系统的影响。考虑到动静压信号表决值误差主要影响飞机纵向飞行品质，现对涉及到的纵向阻尼比、操纵期望参数、稳定储备等参数及时域响应特性进行评估。

2.1 计算模型

以配平飞行状态作为研究的基准状态并计算飞机纵向大导数，建立小扰动模型，由于计算方式为定高定速，故纵向二自由度小扰动方程描述如下：

其中A、B、C、D分别为：

以飞机线性小扰动方程求出飞机纵向状态空间矩阵A，求A阵的特征根，则得到飞机纵向模态。

通常情况下，飞机纵向特征方程具有一对大的共轭复根和一对小的共轭复根（或两个小的实根），短周期模态特性主要受大的共轭复根影响，因此可以根据大的共轭复根计算飞机的纵向模态特性。

纵向模态特性近似计算公式：

国内某技术标准185-1986规定，操纵期望参数标准1在0.28～3.6之间，标准2在0.16～0.28以及3.6～10之间，标准3在0.16～0.28之间。短周期阻尼比ξ应在表1所示范围内。

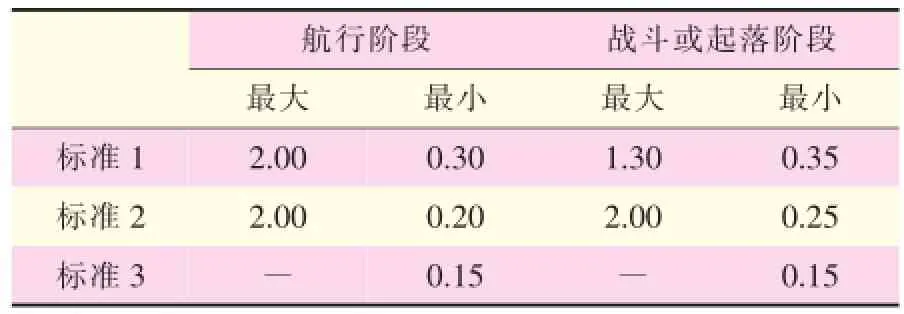
表1 国内某技术标准185-1986短周期阻尼比标准

国内某技术标准2191-1994规定，在飞机可用包线范围内，相位裕度不小于45°，幅值裕度不小于6dB。

2.2 误差影响分析

针对飞控系统动静压表决值较真实静压小4kPa，动压大4kPa的误差状态，进行短周期模态特性、稳定储备及时域仿真计算分析，短周期模态特性计算见表2，稳定储备结果见表3，典型时域仿真结果见图3。

2.3 分析结论

从以上分析结果可以得出：

表2 纵向短周期模态特性对比

表3 稳定储备结果对比

图3 时域响应曲线对比

1）正常状态纵向短周期模态特性均满足国内某技术标准185-1986标准1要求，误差状态大部分状态点仅满足标准2、标准3要求，飞行品质降级；

2）误差状态与正常状态相比，阻尼明显降低，阶跃过程中飞机纵向反应有明显超调和震荡现象，超出操纵预期；

3）误差状态较正常状态稳定储备大都降低，个别状态点甚至不满足国内某技术标准2191-1994的要求。

由此可见，多功能探头静压误差将影响飞控系统的性能，导致飞行品质降级，系统稳定储备降低。

3 处理方式

某飞机使用的多功能探头由压力受感器和压力解算器组成，其中压力受感器为空速管和风标的组合，压力解算器将空速管感受迎风的气流解算出总压，将风标上的气孔感受的气流解算出静压。在未加入修正公式时，由于安装误差，传感器本身解算问题等造成传感器与真实气压值存在偏移；而由于风标上的小孔位置进行了下凹处理，在经过湿冷空气时，容易被水汽附着，凝成水滴，覆盖进气的小孔，造成静压产生较大的跳变误差。

由此可见，要减小多功能探头动静压信号误差，必须进行数据校准及风标形面处理，这意味着巨大的工作量与时间成本。在未进行这些工作时，为使飞控系统仍有足够余度及精度的动静压信号可用，可对信号的使用方式进行更改。

3.1 更改内容

从试飞数据可以看出，多功能探头总压精度满足要求，可以使用，则动静压信号的使用方式进行如下更改：将左、右L形空速管的静压信号各分出一路给左、右多功能探头用于解算；取消左、右多功能探头到飞控计算机的静压信号。

更改后，左/右多功能探头使用左/右L形空速管传输的静压信号与本身感受的总压信号，解算出两余度动、静压信号，发送给飞控计算机。L形空速管同样解算出两余度动、静压信号发送给飞控计算机。

3.2 更改后信号精度

L形空速管总、静压信号均已经过校准，精度满足要求，而从试飞数据可看出，多功能探头总压信号也满足要求。因此更改后传感器提供的四余度动、静压精度均满足要求，可供飞控系统直接使用。

3.3 任务可靠性计算

在动静压信号使用方式更改后，多功能探头与L形空速管共用了静压信号，在后者静压故障时，前者也将失效，因此飞控系统任务可靠性较更改前势必有所降低。国内外战斗机因飞控系统故障导致任务失效的概率指标为不大于1×10-5，为确保更改后系统可靠性仍满足指标要求，需进行任务可靠性计算。

3.3.1 计算模型

在多余度飞控系统任务可靠性计算时，一般将提供每个余度信号的传感器或其他部件建立表决模型（r/n（G）模型），然后将各个模型进行串联，求出整个系统的可靠性。由此可见，对系统任务可靠性影响最大的必然是可靠性最低的模型，而可靠性相对较高的模型影响较小。

为便于分析，本文仅进行大气数据传感器的任务可靠性计算，在其失效率的数量级足够小时，便可认为不影响整个飞控系统的可靠性。更改前后任务可靠性模型见图4，计算公式如下：

其中λ为部件失效率，MTBF为部件平均故障间隔时间，R为部件可靠性，t为系统工作时间，Rs(t)为模型可靠性，n为系统部件数，r为表决数。

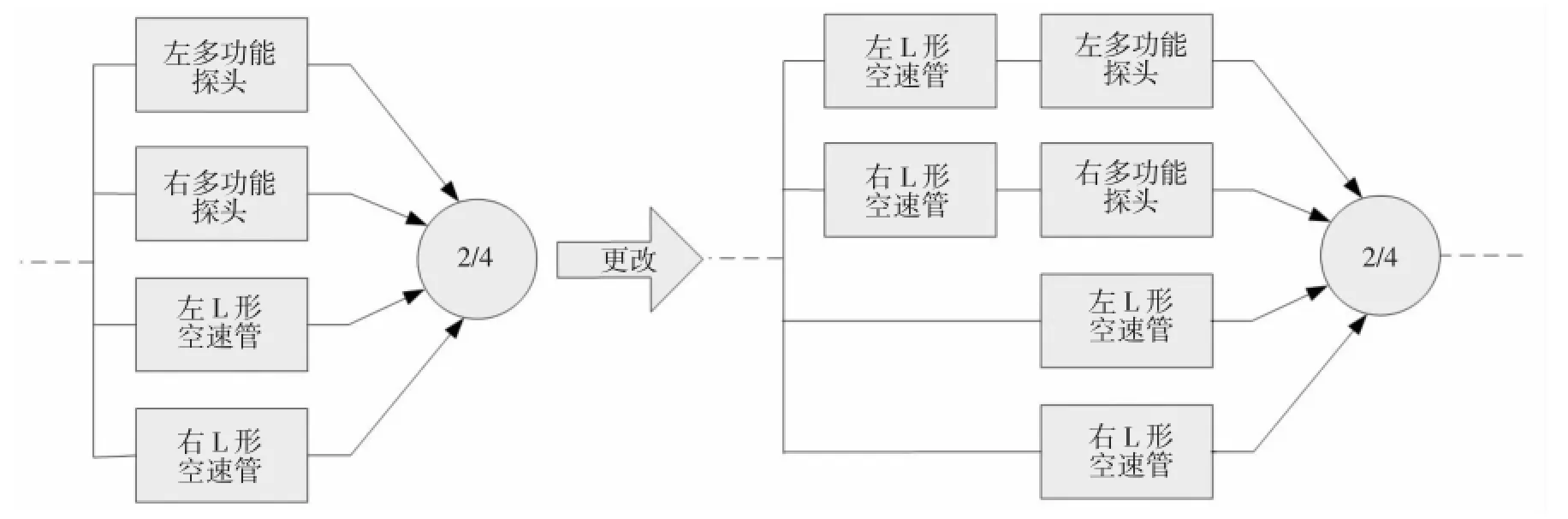
图4 更改前后任务可靠性模型

3.3.2 计算结果

查阅相关资料，多功能探头MTBF为4000小时，L形空速管为1000小时。假设系统工作时间为1小时，对更改前后大气数据传感器的任务可靠性进行计算。

经计算，更改前大气数据传感器任务失效率为6×10-10，更改后为5×10-9，数量级仍然远小于10-5，可认为基本不影响系统整体可靠性。因此，更改后系统任务可靠性有所降低，但仍满足指标要求。

4 结语

本文针对多功能探头传感器精度不足而导致飞控系统动静压信号误差较大的问题，结合余度管理逻辑，进行仿真分析，明确了误差对飞控系统的影响，最后提出了将L形空速管静压信号提供给多功能探头解算的方法，并进行了任务可靠性计算，解决了动静压误差较大问题，保证了飞机飞行品质及飞控系统的可靠性。

在需使用新的空速管未校准的空速管时，可参考本文的方法进行对飞控系统的影响分析，并在必要时选择使用其较准确的信号。

[1]宋翔贵，等.电传飞行控制系统.北京：国防工业出版社，2003.

[2]《飞机设计手册》总编委会.飞机设计手册第12册·飞行控制系统和液压系统设计.北京：航空工业出版社，2013.

>>>作者简介

张欢，男，1988年出生，2010年毕业于南京航空航天大学，工程师，现从事飞行控制系统总体设计工作。

Analysis and Treatment on Static and Pitot Signal Error Effecting FCS

Zhang Huan,Zou Junjun,Rao Mingbo,Zeng Xing,Huang Yongqiang,Yang Zhensheng
(AVIC-HONGDU,Nanchang,Jiangxi,330024)

Static and pitot signals from multifunctional probe on an aircraft which are not calibrated have greater errors.After confirming the applicable signals used by FCS is error with consideration on redundancy management logics,this paper depicts the simulation analysis on longitudinal system damping ratio,desired control parameters,stability reserve and time domain response characteristic,further clarifies that the error has effects on the flight quality and stability reserve and provides the resolutions in the final.

FCS;Static and pitot signal;Error analysis

2016-07-02）