电火工品桥带温升数学模型及可靠性设计应用

石 蓝，杨安民，张迎春，王元和，李占英

（陕西应用物理化学研究所，陕西 西安，710061）

电火工品桥带温升数学模型及可靠性设计应用

石 蓝，杨安民，张迎春，王元和，李占英

（陕西应用物理化学研究所，陕西 西安，710061）

依据焦耳-楞次定律及傅里叶导热定律，建立了恒流激励下电火工品桥带温升的数学模型，得到了药剂不同位置处的温度分布，并给出了发火电流与安全电流的计算方法。利用感度升降法分别对两种桥带式电火工品的发火感度进行了测试，研究结果表明理论计算与试验结果吻合较好，桥带温升数学模型合理，可以用于桥带式电火工品的输入可靠性和安全性设计。

电火工品；桥带；温升模型；感度；可靠性

目前桥带式电火工品以高钝感、高安全和抗电磁干扰等优良特性得到广泛应用。王凯民等[1]推导了桥带式电火工品安全电流的计算公式，但没有考虑桥带外形尺寸、陶瓷片和药剂等材料参数的影响。杨正发等[2-3]建立了桥带式电火工品的传热模型，但该模型没有给出药剂不同位置的温度分布。周庆等[4]给出了桥带式电火工品的一维球体非稳态导热模型，但该模型求解过程较为复杂，难以得到解析解，且未与电火工品的可靠性及安全性设计相结合。

本文建立了恒流激励下桥带式电火工品的桥带温升模型和药剂不同位置处的温度分布，并给出了发火电流和安全电流的理论计算方法，用感度升降法测试并计算得到了恒流激励下桥带式电火工品在置信度γ=0.95、可靠度R=0.999条件下的发火电流，试验结果与理论计算吻合较好，表明建立的温升数学模型可指导桥带式电火工品的发火可靠性及安全性设计。另外，给出了感度分布服从Logistic分布的电火工品50％发火电流和50％安全电流的估算方法。

1 桥带温升数学模型

电火工品桥带温升过程可描述为：火工品通入恒流激励，桥带将电能转化为热能并逐渐升温，该过程遵守焦耳-楞次定律；桥带在温升的同时将热量传递到陶瓷片和药剂，该过程符合傅里叶导热定律，电火工品发火单元示意图如图1所示。

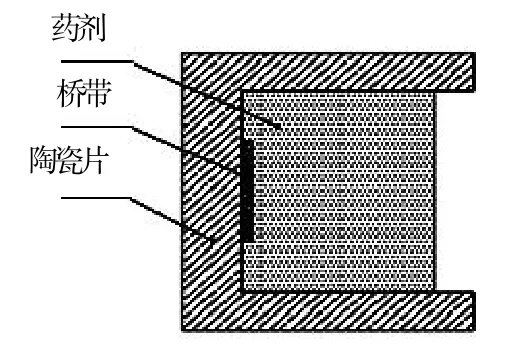
图1 发火单元示意图Fig.1 Firing unit model

由于一般情况下桥带式电火工品的发火区域相对药剂及陶瓷片的体积较小，桥带散热面积较大，可将药剂和陶瓷片导热区域看作半个空心球壁，内热源为直径为2r1=d（d为桥带厚度）的球体，其中药剂球壁与陶瓷片球壁的厚度不同，球壁传热示意图见图2。

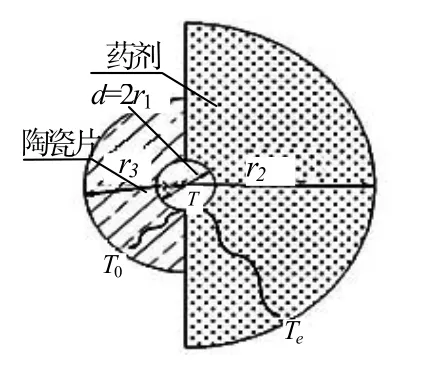
图2 球壁传热示意图Fig.2 Heat conduction model of spherical shell

对该模型做如下假设：（1）忽略药剂化学反应放热对系统温升的影响；（2）只考虑桥带与药剂、桥带与陶瓷片之间的热传导，忽略其它传热方式；（3）桥带、药剂和陶瓷片的导热系数、比热、密度不随温度的变化而变化。根据能量守恒原理及傅里叶导热定律[5]，恒流激励下桥带温升方程为：

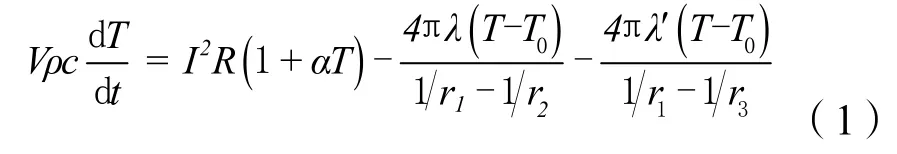
式（1）中：V为桥带体积，m3；ρ为桥带材料密度，kg/m3；c为桥带材料比热，J/(kg·℃) ；t为通电时间，s；I为输入电流，A；R为桥带电阻，Ω；α为桥带材料电阻温度系数，℃-1；λ为药剂导热系数，W/(m·℃)；λ＇为陶瓷片导热系数，W/(m·℃) ；T为桥带温度，℃；T0为初始环境温度，℃；r1=0.5d，为桥带表面到桥带中心的距离，m；r2=5d，为药剂球壁外表面到桥带中心的距离，m；r3=2d，为陶瓷片球壁外表面到桥带中心的距离，m；d为桥带厚度，m。

式（1）中等号左边为桥带温升吸热速率，等号右边第1项为桥带通入电流产热速率，第2项为桥带向药剂散热速率，第3项为桥带向陶瓷片散热速率。由初始条件T |t=0=T0，对式（1）求解得：

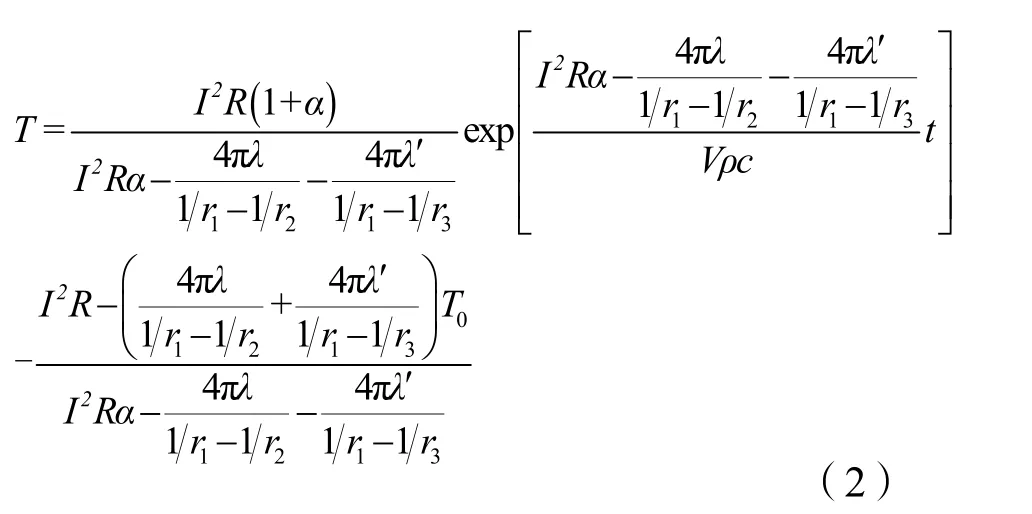
由一维稳态导热情况下球壁温度分布公式求得药剂温度分布为：

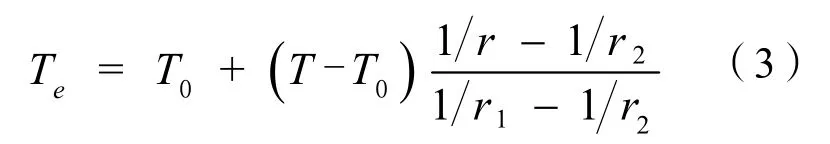
表1～3给出了材料基本参数。其余数据为：桥带体积V=1.75×10-10m3，桥带厚度d=0.03mm，桥带电阻R=1Ω，初始温度T0=20℃。

表1 桥带材料属性参数[6]Tab.1 Material parameters of bridge strip

表2 药剂材料属性参数[7-8]Tab.2 Material parameters of explosive

表3 陶瓷片材料属性参数Tab.3 Material parameters of ceramic

由式（2）～（3）即可求出给定电流和通电时间条件下的桥带温升和药剂温度分布情况，如图3～4所示。

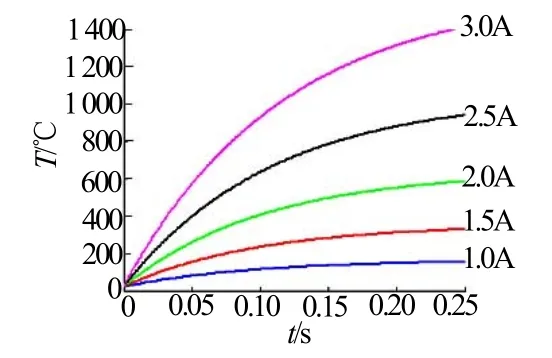
图3 不同输入电流下桥带温升曲线Fig.3 Temperature of bridge strip vs time under different current

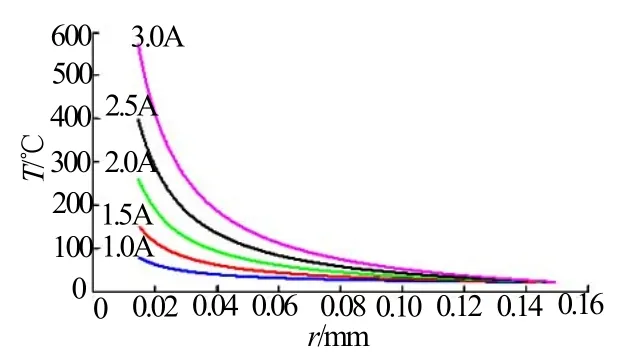
图4 不同输入电流下不同位置处药剂温度分布(t=50ms)Fig.4 Temperature of explosive vs distance under different current

2 感度升降法试验

利用感度升降法测试分别装有1#桥带和2#桥带（如图5所示）试验件的临界发火电流和临界不发火（安全）电流。其中V1=1.75×10-10m3，V2=3.52× 10-10m3，d=0.03mm，R=1Ω，T0=20℃，其余数据均参见表1～3。在不发火感度试验中，由于试验条件限制，2#试验件结果报出数量未达到要求的30发，因而没有得到安全电流的数据。感度升降法试验数据如表4～6所示。根据桥带和药剂的温度分布图（图3～4），结合电火工品发火条件（热点起爆原理，既与桥带表面接触药剂的温度达到药剂爆发点）即可求得发火电流与安全电流。计算发火电流时，考虑到电火工品在极短时间（通常为2～3ms）即可发火，认为与桥带表面接触药剂的温度达到瞬间爆发点即可发火；计算安全电流时，由于通电时间长（5min），认为与桥带表面接触药剂的温度达到5s爆发点方可发火。

由表2中LTNR的瞬间爆发点及5s爆发点，结合公式（1）即可得到1#试样与2#试样的发火电流（通电时间2.5ms）及安全电流（通电时间5min）。试验结果与计算结果对比见表7。

表4 1#试样发火感度试验结果Tab.4 Results of firing sensitivity test of sample 1#

表5 1#试样不发火感度试验结果Tab.5 Results of non-firing sensitivity test of sample 1#

表6 2#试样发火感度试验结果Tab.6 Results of firing sensitivity test of sample 2#

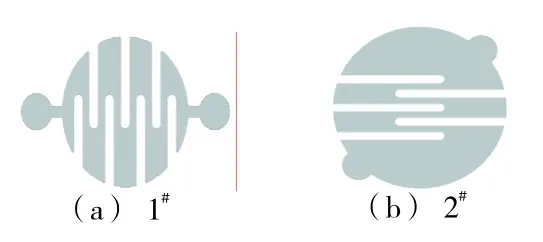
图5 桥带形状Fig.5 Shape of bridge strip

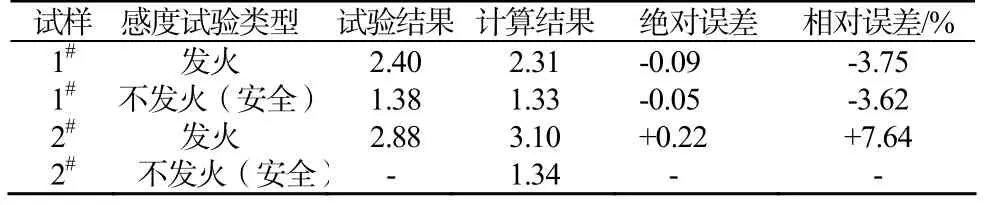
表7 试验结果与计算结果对比 (A)Tab.7 Comparison of caculation results with experimental results

由表7数据对比可以看出理论计算结果与试验结果误差较小。误差产生的原因一方面由于桥带尺寸、药剂密度（对其导热系数产生影响）等参数对计算结果有一定影响；另一方面感度试验时试验样品的个体差异也对试验结果造成一定误差。

3 发火可靠性与安全性设计

在电火工品发火可靠性和安全性设计要求下（给定发火可靠性的置信度和可靠度指标），由桥带温升计算公式（2）可对发火单元（桥带、陶瓷片和药剂）进行优化设计。如通过调整陶瓷片和药剂的材料及性能，并匹配设计不同形状和材料的桥带，再由桥带温升数学模型计算得到发火单元的最优发火电流，进而提高电火工品的固有发火可靠性和安全性。

另外，由桥带温升计算公式可估算产品的50％发火电流与50％安全电流，为感度升降法可靠性与安全性评估试验中初始刺激量的确定提供参考。通常电火工品的输入感度具有对称型logistic分布特性[9]，因此就感度分布服从logistic分布的产品进行可靠性及安全性设计。设计发火刺激量I1对应发火可靠度Rf，设计安全刺激量I0对应安全可靠度Rs，根据产品发火可靠性和安全可靠性定义[1]，有：

50％发火电流为：

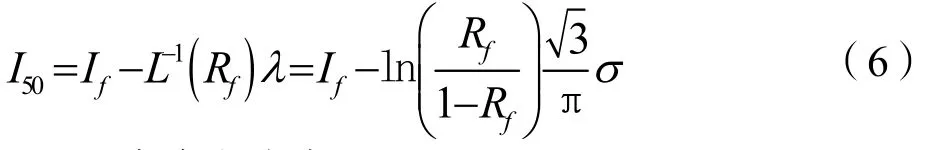
50％安全电流为：

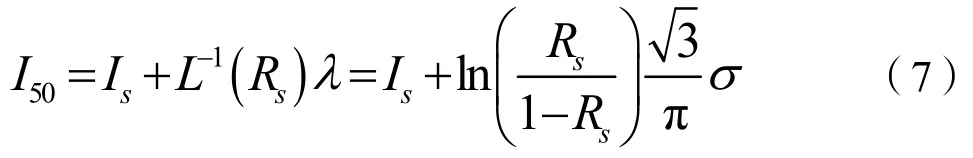
由以上分析可知，利用桥带温升数学模型可优化桥带式电火工品的设计，提高其固有发火可靠性与安全性，同时降低设计成本，提高设计效率，加快产品开发周期。由式（6）～（7）可估算感度升降法试验中的初始刺激量，优化可靠性与安全性评估试验设计，减小试验成本。

4 结论及展望

本文建立的桥带温升数学模型计算结果与感度试验结果吻合较好，通过对桥带式电火工品的发火电流与安全电流进行计算，可为桥带式电火工品的可靠性设计提供参考。通过本文的工作可得出以下结论：（1）基于焦耳楞次定律和傅里叶导热定律的电火工品桥带温升数学模型，可计算得到直流激励下的桥带温升和散热、药剂温度分布、发火电流及安全电流。（2）通过对电火工品桥带温升和药剂温度分布的计算，可指导发火单元的优化设计，提高电火工品的可靠性与安全性。（3）对于感度分布服从logistic分布的产品可估算其50％发火电流与50％安全电流。

由于桥带与药剂、桥带与陶瓷片间的传热较为复杂，药剂化学反应对系统温升有一定影响，实际情况中药剂、桥带及陶瓷片参数和质量一致性与计算模型存在一定差异，而且感度试验中存在人为及环境等因素的影响，这些都可能对发火单元桥带温升数学模型的计算结果带来一定影响，需在今后的研究工作中加以考虑，使计算结果更加准确。

[1]王凯民,张学舜.火工品工程设计与试验[M].北京:国防工业出版社,2010.

[2]杨正发.一种姿态控制发动机点火装置简介[J].固体火箭技术,2000,23(1):9-12.

[3]杨正发,杨翼英.桥带制作线切割工艺研究[J].航天制造技术,2006(4):10-13.

[4]周庆,焦清介.电流激励Ni-Cr 桥带式电火工品发火模型[J].含能材料,2014(22):824-827.

[5]陶文铨.传热学[M].西安:西北工业大学出版社,2006.

[6]GJB 1667-93 火工品用精密电阻合金规范[S].北京:国防科学技术工业委员会,1993.

[7]蔡瑞娇.火工品设计原理[M].北京:北京理工大学出版社, 1999.

[8]钟一鹏,胡雅达,江宏志.国外炸药性能手册[M].北京:兵器工业出版社,1990.

[9]穆慧娜.火工品可靠性设计若干研究[D]:北京:北京理工大学, 2009.

Temperature Rise Mathematical Model of Bridge Strip Electric Initiator and Its Reliability Design

SHI Lan, YANG An-min, ZHANG Ying-chun, WANG Yuan-he, LI Zhan-ying
(Shaanxi Applied Physics and Chemistry Research Institute, Xi′an, 710061)

Based on the Joule Lenz’s law and Fourier heat conduction law, a mathematical model of the temperature rise of bridge strip under direct current excitation was established, the temperature distribution at different position of charge was obtained, and the theoretical calculation method of the firing current and safety current was also proposed. The firing sensitivity of two electric initiators was measured by Bruceton method. The results show that the theoretical calculation results are in good agreement with the experimental results, which indicate the bridge strip temperature rise model is reasonable and can be used in the input reliability and safety design on bridge strip electric initiator.

Electric explosive device；Bridge strip；Temperature rise model；Sensitivity；Reliability

TJ450.1

A

1003-1480（2016）06-0024-04

2016-10-17

石蓝（1991 -），女，在读硕士研究生，主要从事先进火工技术研究。