基于模糊函数的超声信号高斯模型参数分辨率分析

马伏花，卢振坤

(广西民族大学信息科学与工程学院，广西南宁530006)

基于模糊函数的超声信号高斯模型参数分辨率分析

马伏花，卢振坤

(广西民族大学信息科学与工程学院，广西南宁530006)

模糊函数是一种超声检测系统性能分析的重要工具。文中首先给出超声信号高斯模型，接着推导该模型的模糊函数，最后讨论分析与探测距离和移动目标速度相关的超声检测系统的时间和频率分辨率，并给出了相关超声检测系统参数选择的参考。理论推导和仿真结果表明：辨别运动着的目标，用长持续时间的信号，即窄带宽；辨别近距离的目标，用短持续时间的信号，即宽带宽。

超声；模糊函数；分辨率分析；高斯模型

0 引言

超声探测技术是无损检测技术领域中一种非常重要的手段和方法。它是通过对检测材料发射超声波，然后接收回波加以分析来探测这些材料内部和表面的缺陷，评价材料的物理和力学性质。由于超声检测方法具有灵敏度高、设备比较简单、对人身无伤害等优点，被广泛应用于无损检测技术中[1-3]。

复杂材料结构以及噪声，往往会造成回波信号一些参数特征的变化，比如频率消散、相位漂移、时间延迟等。实际探测中，材料厚度小或者被测材料层与层之间间隔小，往往会造成回波重叠、参数测量困难和误差；这种情况还表现在材料内部2个距离很近的小尺寸缺陷上，由于回波重叠严重，无法判断缺陷的个数、大小及准确位置；而且，随着超声传播的深度增加，回波衰减加重。目前，提高探测精度是超声探测技术中一个具有挑战性的问题，主要通过2种途径来提高分辨率：其一是改进或更新系统硬件(如增大系统带宽)来提高系统理论分辨率；其二是利用数据后处理方法来提高分辨率。由于改进或更新系统硬件代价大、周期长，而且受限于技术的发展，故基于现有的硬件设备，通过建立物理模型和数学模型来研究提高超声探测精度的数据后处理技术，则具有更重要的理论意义和应用价值。

对很多超声检测系统，超声回波信号可以用带参数的高斯模型表示，如回波带宽、波达时间、中心频率、幅度和相位等[4]， 这些参数与被探测材料的物理特性相关。常用来估计回波信号参数的方法有互相关法、阈值比较法、滑动窗法[5]以及时频分析法[6-8]等，而参数值的选择将影响探测分辨率。

模糊函数是一种有效的信号时频分析工具，其被广泛应用于光学、音乐和雷达[9-11]等。它有助于提供改善超声回波参数性能的波形的选择。目前模糊函数的应用研究主要集中在雷达探测分辨率的分析上[12-13]。本文给出了超声回波高斯模型以及推导它的一些数学性质，并讨论分析影响系统分辨率的参数。

1 超声信号高斯模型

根据超声回波的物理特性，用超声换能器脉冲响应幅度的修改模型s(θ，t)表示接收到的有用回波信号[4]：

s(θ，t)=βe-α(t-τ)2cos(2πfc(t-τ)+φ)，

(1)

其中θ=(α，τ，fc，φ，β)，α指带宽，τ指到达时间，fc指中心频率，φ指相位，β指幅度系数。

回波模型做加性白噪声(WGN)处理得：

x(t)=s(θ，t)+v(t)，

(2)

其中v(t)为加性高斯白噪声。

特征参数向量θ中的5个参数在均匀的传输路径及理想表面反射物上的物理意义：到达时间τ与反射物体的位置相关，也与传输路径的长度和在该介质中超声传播速度直接相关；带宽因子α反映接收到的回波带宽，也反映回波在时域上的持续时间；中心频率fc由换能器中心频率和传输路径的频率特性共同决定，换能器的中心频率一般已知，故fc反映传输路径的频率特性；回波的幅度系数β和相位φ与反射物的阻抗、大小及方位有关。该模型的优点是得到了检测参数的高分辨率估计，并抑制了噪声。

2 高斯模型的模糊函数和模糊图

用某种单一的方法描述发射信号或回波信号是有利的，它们可以与利用等效的、相当普遍的特征所表示的方法进行比较。为了这个目的，我们利用模糊函数。它最早由伍德瓦尔德引入，并且广泛地用来分析雷达的特征[12-13]。

2.1 模糊函数

根据定义[14]，模糊函数可以写成如下的形式：

(3)

根据高斯回波模型，它的复包络Z(t)具有形式：

Z(t)=A(t)=βe-α(t-τ)2，

(4)

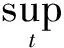
(5)

经过运算得到：

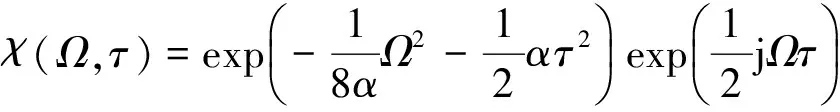
(6)

有效持续时间为：

(7)

2.2 模糊图

模糊函数的形状通常用其模的平方|χ(Ω，τ)|2表示，可用|χ(Ω，τ)|2代替函数χ(Ω，τ)作为模糊函数，模糊图用来获得|χ(Ω，τ)|2形状的方向性估计。为此，可由条件|χ(Ω，τ)|2=k2，选择一个固定的k值来确定下述形式模糊函数方程：

(8)

这里F(·)表示一个函数。

根据以上定义，由式(6)得：

(9)

即：

(10)

两边取对数得：

(11)

变形得到：

(12)

由此可知每一个k值所对应的模糊图是一个椭圆。

下面我们来讨论k值的确定。

我们对式(9)求二重积分：

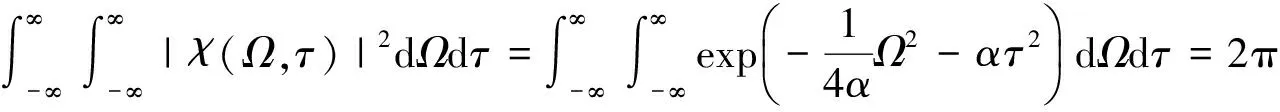
上述结果为模糊体的体积。有多种方法可以用来选择k值，下面介绍2种方法。

2.2.1 方法一

由模糊体的体积，我们选择构成一个单位高度的柱体，它具有垂直于平面(Ω，τ)的母线，该柱体的底面为区域D，并令该主体体积等于模糊体的体积，即：

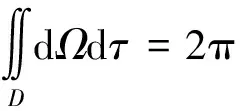
(13)

这样k值可由式(13)确定，这里积分区域D依赖于条件|χ(Ω，τ)|2=k2。不难看出，由式(12)可知Ω和τ的取值范围：

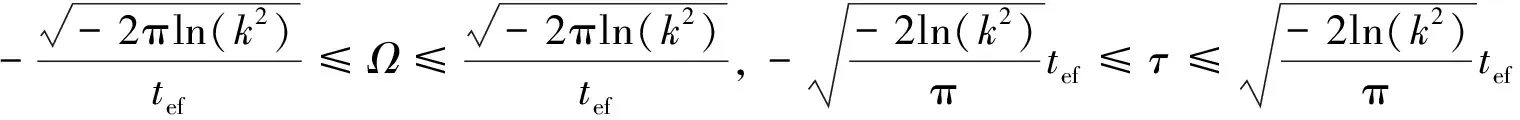
图1 当Ω∈[0，20]，τ∈[0，2]时的模糊函数值Fig.1 Value of the ambiguity function forΩ∈[0，20]，τ∈[0，2]

可以看出，当k值很小时，可能导致Ω和τ趋向于无穷大，影响区域D的确定，我们通过式(9)来画图1，这里取Ω∈[0，20]，τ∈[0，2]。

从图1可以看出，当Ω和τ增大时，模糊函数值迅速趋向于0，则在有限的区域内可以使模糊体的体积接近于2π，因此k的取值不影响区域D的确定。而在此选择式(10)所确定的椭圆面为区域D，由式(12)可得：

(14)

由式(14)可求出：

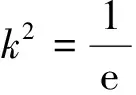
(15)

将k代入方程组(16)：

(16)

整理得：

(17)

2.2.2 方法二

从几何角度来看，模糊图在(Ω，τ)坐标系中可以用曲线的形式构成，于是可用平行于(Ω，τ)的平面在一系列值k1，k2，…，kn上截取|χ(Ω，τ)|2表面求出模糊图。

我们取k1=0.167、k2=0.333、k3=0.500、k4=0.667、k5=0.833，绘图结果如图2所示。由图2可知，合理地选择k值对于坐标的分辨率可由模糊图和对应的坐标轴(Ω，τ)之间的交点来确定。

图2 模糊函数和模糊图Fig.2 The ambiguity function and the ambiguity graph

2.3 结果讨论

由式(12)可得：

(18)

解下列方程组(19)：

(19)

得：

(20)

图3 参数τ相对于参数Ω的变化情况(k=0.4)Fig.3 The rate of change of τ relative to Ω(k=0.4)

显然，当选定某个k值后，Ωτ=-2lnk2为常数。

由式(18)对Ω求导得：

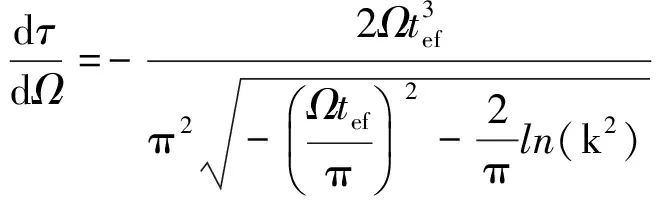
(21)

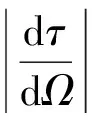
3 结论

模糊图可以用来估计超声信号系统对于时间(检测目标的距离)和频率(目标运动的速度)的分辨率。对于给定的信号形式，值τ和Ω可以确定系统的分辨率。理论推导和仿真结果表明：为了辨别运动着的目标，采用长持续时间的信号，即窄带宽；辨别近距离的目标，采用短持续时间的信号，即宽带宽。

[1] HEIN A， O’BRIEN W D. Current time-domain methods for assessing tissue motion by analysis from reflected ultrasound echoes[J]. IEEE Trans Ultrason， Ferroelect， Freq Contr, 1993，40(2)：84-102.

[2] CHEN E J， JENKINS W K， O’BRIEN W D. The impact of various imaging parameters on ultrasonic displacement and velocity estimates[J]. IEEE Trans Ultrason， Ferroelect， Freq Contr， 1994， 41(3)：293-301.

[3] 郭纲，王树勋，孙晓颖，等.超声信号的双指数模型及参数确定方法[J].电子学报， 2009， 37(7)：1501-1504.

[4] DEMIRLI R， SANIIE J. Model-based estimation of ultrasonic echoes Part I：analysis and algorithms[J]. IEEE Trans Ultrason， Ferroelect， Freq Contr， 2001， 48(3)：787-802.

[5] BARSHAN B， AYRULU B. Performance comparison of four time of flight estimation methods for sonar signals[J]. IEEE Electronics Letters， 1999， 34(16)：1616-1617.

[6] YUFENG L， DEMIRLI R， CARDOSO G， et al. A successive parameter estimation algorithm for chirplet signal decomposition[J]. IEEE Trans Ultrason， Ferroelect， Freq Contr， 2006， 53(11)：2121-2131.

[7] HOSEINI M R， XIAODONG W， ZUO M J. Estimating ultrasonic time of flight using envelope and quasi maximum likelihood method for damage detection and assessment[J]. Measurement， 2012， 45(8) ：2072-2080.

[8] ZHENKUN L， CUI Y， GANG W. Optimal transform order of fractional fourier transform for decomposition of overlapping ultrasonic signals[J]. IEICE Transactions on Fundamentals of Electronics， Communications and Computer Sciences, 2014， E97-A(1)：393-396.

[9] MECKLENBRAUKER W， HLAWATSCH F. The wigner distribution：theory and applications in signal processing[M]. Amsterdam：Elsevier， 1997：59-133.

[10] AUSLANDER L， TOLIMIERI R. Characterizing the radar ambiguity functions[J]. IEEE Trans Inf Theory, 1984， 30(6)：832-836.

[11] GOGINENI S， RANGASWAMY M， RIGLING B D， et al. Ambiguity function analysis for UMTS-based passive multistatic radar[J]. IEEE Trans Signal Process, 2014， 62(11)：2945-2957.

[12] 刘领容，王凌，姚远程，等.复合线性调频信号的模糊函数分析[J].西安理工大学学报，2011，27(4)：481-485.

[13] 张容权，黄钰林，杨建宇.双基地线性FMCW雷达信号模糊函数及分辨特性[J].电子与信息学报，2007，29(4)：836-840.

[14] HUSSAIN M G M. Ambiguity functions for monostatic and bistatic radar systems using UWB throb signal[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011， 47(3)：1710-1722.

[15] ZHENKUN L， CUI Y， DONGHONG Q, et al，Estimating the parameters of ultrasonic echo signal in the gabor transform domain and its resolution analysis[J]. Signal Processing, 2016， 120：607-619.

[16] ZHENKUN L， CUI Y， GANG W. Hilbert transform based time-of-flight estimation of multi-echo ultrasonic signals and its resolution analysis[J]. IEICE Transactions on Fundamentals of Electronics， Communications and Computer Sciences, 2014， E97-A(9)：1962-1965.

(实习编辑 李 朝)

(责任编辑 马殷华)

Parameter Resolution Analysis of Gaussian Model ofUltrasonic Signal Based on Fuzzy Function

MA Fuhua， LU Zhenkun

(College of Information Science and Engineering， Guangxi University for Nationalities， Nanning Guangxi 530006, China)

Fuzzy function is an important tool for the performance analysis of ultrasonic testing systems. In this paper， the ultrasonic Gaussian model is proposed at first. Then, the fuzzy function of the ultrasonic signal for Gaussian model is derived in detail. Finally， the resolution of time and frequency for an ultrasonic testing system is analyzed， which is related to distance of detection target and speed of moving target. Reference for selecting parameter value of an ultrasonic testing system is provided. Theoretical derivation and simulation results show that it is better to discern moving targets by using a narrow bandwidth signal. And for distinguishing short-range targets， a short-duration signal is ideal.

ultrasonic； fuzzy function； resolution analysis； Gaussian model

10.16088/j.issn.1001-6600.2016.04.004

2016-06-03

国家自然科学基金资助项目(61561008)；广西自然科学基金资助项目(2014GXNSFBB118005)；广西高校科研资助项目(ZD2014124)；广西混杂计算与集成电路设计分析重点实验室开放课题资助项目(HCIC2014)；广西民族大学科研资助项目(2014MDQD019, 2015MDYB014)

卢振坤(1979—)，男，广西百色人，广西民族大学副教授，博士。E-mail: lzk06@sina.com

TB911.7

A

1001-6600(2016)04-0026-06