对物理实验测量仪器读数的思考

□赵重阳

（温州市第二十二中学，浙江温州 325003）

对物理实验测量仪器读数的思考

□赵重阳

（温州市第二十二中学，浙江温州 325003）

物理实验中对测量仪器读数时有读数不确定度，测量结果的报告中有测量不确定度.测量仪器的示数是实验中的原始数据，而计算测量误差和测量不确定度是读数之后处理数据时的工作，故读数不受测量误差或测量不确定度的制约.指针式仪表在读数时应按其指针的粗细、最小分度的宽度以及测量者的视力分辨能力进行估读.

读数不确定度；测量不确定度；原始数据；读数规则

指针式仪表的读数规则在中学一直比较混乱，有观点认为读数时要考虑仪器的误差（精度），也有观点认为读数时要考虑仪器的测量不确定度[1].实际上，测量仪器的示数是原始数据，而不是测量结果，测量结果是对原始数据进行处理而得到的，数据处理中需要考虑误差和测量不确定度.

一、读数不确定度与测量不确定度

实验中对“估读”类测量仪器读数时，同一次测量因读数者的不同读出的数据往往存在差异，这种差异是由测量者的视力分辨能力不同而引起的.如果测量者根据测量仪器的指针粗细和最小分度宽度，分辨出指针宽度占最小分度宽度的，那么该测量者的读数不确定度为（单位）.例如，利用毫米刻度尺测量某一物体的长度时，若甲能分辨最小刻度的，那么甲读数产生的读数不确定度为如果甲的读数为6.32cm,那么被测物体的长度在6.31cm与6.33cm之间.读数不确定度与测量者的视力分辨能力和不良读数习惯有关，若侧坐斜视读数会增大读数不确定度.

由于测量误差的存在而对被测量值不能肯定的程度称为测量不确定度，实际上是对误差的估算.测量不确定表达了测量结果的精确度，它可以通过定量计算得出的结果来衡量[2].测量结果中不确定度的值是由读数、仪器误差等多种因素引起的不确定度的总和.测量不确定度的来源主要有：测量的定义不完整、被测量的测量方法不理想、取样的代表性不够、测量过程中环境的影响、读数存在人为偏差、测量仪器的局限性、在相同条件下被测量在重复观测中的变化等.即测量结果中不确定的值是由读数、仪器误差等多种因素引起的不确定度的总和.

二、读数与不确定度的关系

读数结果受测量者的读数不确定度制约，而不受测量仪器的测量不确定度所制约.读数获取的是原始数据，而计算测量不确定度是获取原始数据之后处理数据时的工作.原始数据是没有经过加工（数据修约）的数据，读数时不受仪器的误差或测量不确定度所制约.常用测量仪器可分为“直读”类和“估读”类.前者的读数是不需要估读的，此类仪器包括游标卡尺、分光计、机械秒表和电阻箱等；后者的读数包括可靠部分和估读部分，其估读规则应该统一，即按照仪表指针的粗细、仪器最小分度的实际宽度以及测量者的分辨能力所决定[3]，此类仪器包括毫米刻度尺、螺旋测微器、指针式仪表等.

三、对中学物理实验中测量仪器读数的思考

（一）依据误差或测量不确定度进行读数不合理

首先，中学阶段不要求计算误差，也不要求了解或计算测量不确定度.人教版《物理必修1教师用书》指出“能结合具体实验情况，指出什么是系统误差和偶然误差，知道绝对误差和相对误差；理解在相同条件下要提高实验的准确度，要考虑如何减小相对误差”[4].《2012年浙江省物理学科指导意见》指出“会对实验误差作初步分析”.《2015年浙江省普通高考考试说明（物理部分）》指出“了解误差概念，知道系统误差、偶然误差和用多次测量求平均值的方法可减小偶然误差；能在某些实验中分析误差的主要来源；不要求计算误差”.由于在中学阶段既不作仪器误差估算，又不讲仪器级别，而且多数仪器并没有标出精度级别，要求学生计算误差或了解测量不确定度显然是不合理的.其次，读数是获取原始数据，仪器的读数要估读到最小分度的几分之几，应该由指针的粗细和最小分度的实际宽度以及测量者的视力分辨能力所决定，而不受仪器的误差（精度）或测量不确定度所制约.

（二）测量仪器的估读规则

对“估读”类测量仪器的读数时，首先要观察仪器的量程和刻度盘（表盘）的总格数，明确最小分度值；其次，要观察刻度盘上最小分度的宽度和指针的粗细，估计指针的宽度占最小分度宽度的比例，能分辨到指针宽度占最小分度宽度的几分之几，就可估读到最小分度的几分之几.如果指针很细，能分辨到指针宽度占最小分度宽度的十分之一，就可估读到最小分度的十分之一；如果指针较粗或者分辨能力较弱，仅能分辨到指针宽度占最小分度宽度的二分之一，就可估读到最小分度的二分之一.中学阶段常用的估读测量仪器有刻度尺、螺旋测微器和指针式电表，正常情况下学生的分辨能力差异不大，估读规则应该统一且标准明确，可以要求学生估读到测量仪器最小分度的十分之几即可，即读数时读到最小分度的十分位.对于双量程（3A，0.6A）电流表，测量时选用量程3A（最小分度0.1A）与0.6A（最小分度0.02A）时，因指针的粗细和最小分度的宽度相同，故读数时均应读到最小分度的十分位.

特别要指出的是，在实验教学中要让学生知道测量仪器的读数是原始数据，原始数据是记录实验和测量过程中最重要的基础材料，必须做到完整、严格和准确[5].记录数据时应当做到：按照数据规律列出表格；记录的是未经加工的原始数据；物理量必须有单位；有效数字要正确.对于指针式仪表，为防止差错，应先读出原始示值的位置(偏转格数)，再转换成测量值.例如，用量程为150mA，总刻度为75格的电流表（最小分度为2mA）测量电流时，若指针的位置在48.4格，记录数据时先记录48.4格，再转换成96.8mA；若指针的位置在45.0格，记录数据时先记录45.0格，再转换成90.0mA.

（三）对高考试题中读数“答案”的思考

题一 （1990年全国高考，第24题）用伏安法测电阻的实验中，按实验要求选用的电压表的最小分度为0.1伏，电流表的最小分度为0.02安.某学生记录的各组数据如表1所示，在这五组数据中，有效数字位数不符合要求的是第_____组，数据有差错的是第_____组.（参考答案：1，3）

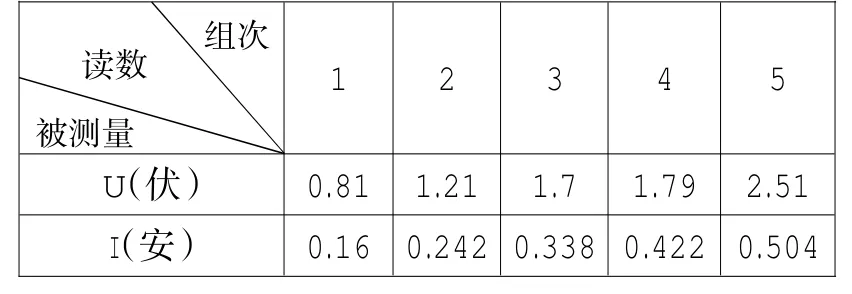
表1

对答案的思考：读数估读到最小分度的十分位.电流表的最小分度为0.02安，电压表的最小分度为0.1伏.本题是对相同宽度的最小分度和相同粗细的指针提出相同的估读要求，即可估读到最小分度的十分位，因此参考答案是合理的.

题二 （2009年安徽高考，第21题）用多用电表进行了几次测量，指针处于a位置，如图1所示.若多用电表的选择开关处于表2中所指的挡位，相应读数是多少？（参考答案：23.0mA，0.57V）

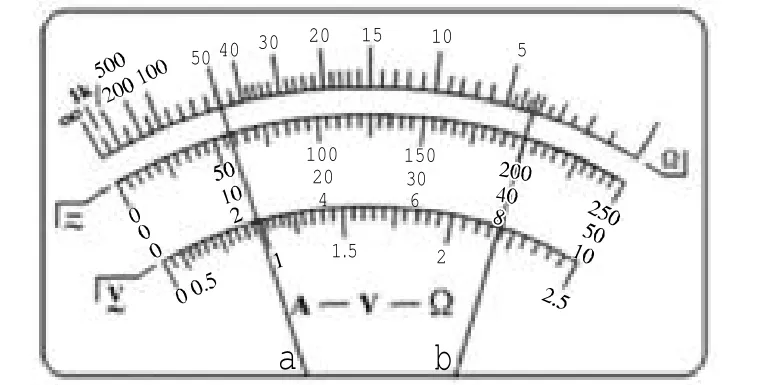
图1

表2

对答案的思考：读数估读到最小分度的十分位.量程为100mA时最小分度为2mA,量程为2.5V时最小分度为0.05V，故答案23.0mA合理，而0.57V不合理，应该是0.570V.

题三 （2010年全国高考，第23题）在某一温度下，电路中的电流表、电压表的示数如图2所示.电流表的读数为____，电压表的读数为___.（参考答案：115 mA，5.00V）

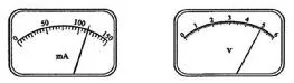
图2

对答案的思考：读数估读到最小分度的十分位.电流表量程为150mA，最小分度为5mA，电压表量程为6V，最小分度为0.1V，故答案115mA不合理，应该是115.0mA,电压示数答案5.00V合理.

题四 （2015年浙江高考，第22题，有改动）小红同学在做“描绘小灯泡的伏安特性曲线”实验时，调节滑动变阻器得到了两组电流表与电压表的实数，如图中的①②所示，电流表量程为0.6A，电压表量程为3V，电流表的读数为：

①_____②_____.（参考答案：0.10A，0.24A）

对答案的思考：读数估读到最小分度的十分位.电流表量程为0.6A，最小分度为0.02A；电压表量程为3V，最小分度为0.1V，故答案0.10A和0.24A均不合理，应该是0.100A和0.240A.

2015年浙江省高考阅卷中第22题的阅卷标准是0.10A或0.100A和0.24A或0.240A均给分.给分标准的调整是因为对读数规则的理解存在争议.解决争议，需要明确实验中测量仪器的读数是原始数据而不是测量结果，读数结果与测量者的读数不确定度相关，但读数规则不受仪器级别或测量不确定度的制约，读数应该按指针的粗细、最小分度的宽度以及测量者的分辨能力进行估读.这样的读数规则不仅标准明确，便于掌握，而且不会给中学实验教学带来混乱.当然，解决读数争议需要教材或教师用书给出合理且明确的读数规则，即实验中获取原始数据时的读数规则.□◢

［1］宋昌杰.对高中物理实验中电表读数的思考[J].物理教师，2015（3）：54-55.

［2］郭悦韶.大学物理实验［M］.北京：清华大学出版社，2012：8-10.

［3］徐承楠.对中学物理实验中测量仪器的读数规则的意见［J］.物理教师，1991（6）：28.

［4］张大昌.普通高中课程标准实验教科书物理（必修1）［M］.北京：人民教育出版社，2010：165.

［5］梁家惠.基础物理实验［M］.北京：北京航空航天大学出版社，2005：22.