基于改进的RIDE⁃VEG模型的随机波下植物消浪数值模拟研究

才 多，徐 凡

（1.上海市水利工程设计研究院有限公司，上海200061；2.河海大学港口海岸及近海工程学院，南京210098）

基于改进的RIDE⁃VEG模型的随机波下植物消浪数值模拟研究

才 多1，徐 凡2

（1.上海市水利工程设计研究院有限公司，上海200061；2.河海大学港口海岸及近海工程学院，南京210098）

文章拓展了平面二维的植物消浪数学模型RIDE⁃VEG，模拟了随机波条件下的植物消浪作用，并考虑波浪破碎，数值结果与各水槽模型试验均吻合良好。模型比较了线性波拆分和均方根波高表征两种方法，发现这两种方法在率定植物拖曳力参数上存在较大区别。能谱分析显示，经过植物后，整个频域内的波能均有衰减，而衰减的幅度在谱峰频率处最大，且低频波大于高频波。考虑植物作用时，由于植物削弱了由于浅水变形引起的波高增大，导致波浪破波点更接近岸线。

随机波；植物消浪；波浪破碎；海岸防护

近年来，由于气候变化、海平面上升等因素，沿海地区风暴、洪涝灾害频发。面对更加剧烈的海岸动力条件，海岸防护设施（如海堤、防波堤等），需要相应提高防护标准。湿地植物作为一种经济、生态的软防护手段，被越来越多地应用到工程中［1］。因此，研究波浪在植物作用下的衰减变形机制，对湿地植物在工程中的应用具有指导意义。

实际近海波浪条件随机而复杂，单纯基于以规则波研究成果［2-5］不能完全满足实际的需求。Dubi［6］首先进行了随机波条件下的植物消浪物理模型试验，而Løvås et al.［7］在其物理试验中考虑了波浪破碎作用。近期Stratigaki et al.［8］，Koftis et al.［9］和Manca et al.［10］联合进行的一系列物理模型试验，综合考察了水草淹没程度、水草密度、波浪周期的影响，以及波能消耗与波浪频率之间的关系。这些物理模型试验研究为理论和数值研究提供了重要铺垫。数值模拟方面，Li et al.［11］利用三维时均雷诺方程模拟了随机波条件下植物对于波浪的衰减作用，并与Dubi［6］的试验进行对比验证。Mendez［12］将波浪破碎和植物引起的能量衰减叠加，得到了一个综合考虑两者作用的线性模型。Ma et al.［13］利用非线性的k⁃ε模型，在只考虑拖曳力作用、忽略植物摆动和惯性力的作用下，模拟了植物作用下斜坡上的波浪破碎过程。

基于随机波的研究虽然已取得一定成果，但其作用机理尚不明确，各家学者的研究结论也不尽相同。本文基于平面二维数学模型——RIDE⁃VEG［2］分别采用线性波叠加和均方根波高表征两种方法，模拟了Du⁃bi［6］和Løvås et al.［7］的物理试验，并讨论了植物作用下随机波波能沿程衰减以及波浪破碎时的波高分布规律。

1 模型简介

Maa et al.［14］基于Chamberlain et al.［15］提出的拓展型缓坡方程，开发了可以在复杂地形条件下，忽略水流作用的平面二维缓坡方程数学模型（RIDE）。才多、诸裕良［2］基于该模型，建立了可以模拟规则波下植物消浪的平面二维数学模型RIDE⁃VEG，模型中采用Kirby et al.［16］提出的非线性频散关系进行修正。模型基本方程如下

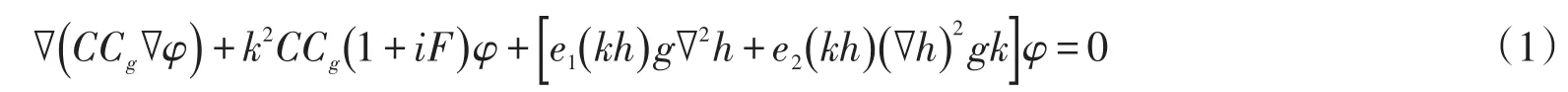
式中：h为水深，φ为速度势函数的水平变化函数，C为波速，Cg为波群速，k为波数，系数和e2(k h)的表达式详见文献［15］。F=Fb+Fbre+Fv，Fb为底摩擦项，Fbre为碎波时的能量耗散项，Fv为规则波作用下植物引起的能量耗散项，如式（2）、式（3）所示

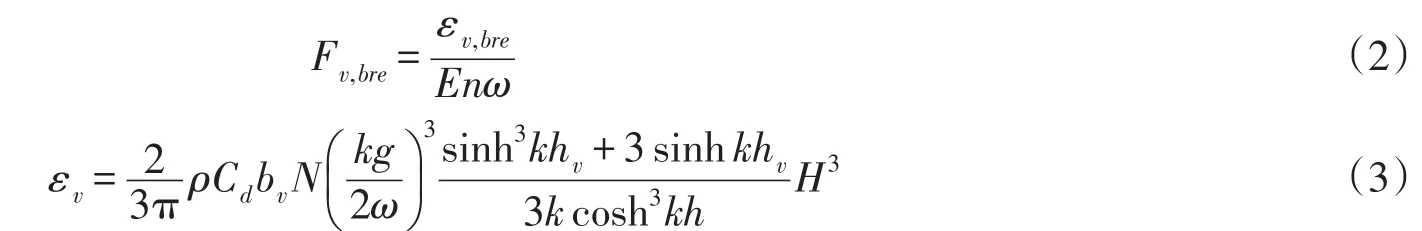
式中：εv代表波能在植物场中的衰减率，E为波能，ω为波浪圆频率，Cd为植物作用的拖曳力系数，bv为植物迎浪面宽度，N为植物密度，hv为植物的高度，H为波高，ρ为水的密度。

本文分别采用了线性叠加和均方根波高表征两种方法模拟随机波。其中，线性叠加法是将随机波视为多个不同频率、不同相位的规则波的叠加，分别计算各成分波在植物作用下的衰减，再将结果线性叠加。考虑如波浪破碎时，线性叠加法不再适用。Mendez et al.［12］直接以均方根波高的形式，推导出了随机波在植物中传播的数学模型，此时波能衰减率εv和破碎引起的能量耗散项εbre具有如下形式

式中：B和γb均为波浪破碎指标，在本文计算中取B=1，γb=0.78，fp为谱峰周期对应的波浪频率。将随机波浪直接以均方根波高的形式表征，可直接将式（4）、式（5）代入RIDE⁃VEG模型进行计算。

2 波浪的沿程衰减数值模拟

Dubi［6］进行的物理试验被广泛应用于随机波条件下的植物消浪数学模型验证。试验水槽长33 m、宽0.5 m、高1.6 m，水槽中央第16.7～26 m处布置长度为9.3 m的人工植物区，植物高度0.2 m，直径0.025 m，植物密度1 200株/m2（图1），采用JONSWAP谱造波，谱峰升高因子γ=3.3，水槽末端设消波设置，可以认为在此处波浪被完全吸收。数值模型的起算点位于距离造波机6.7 m处，其余设定与物理试验一致。

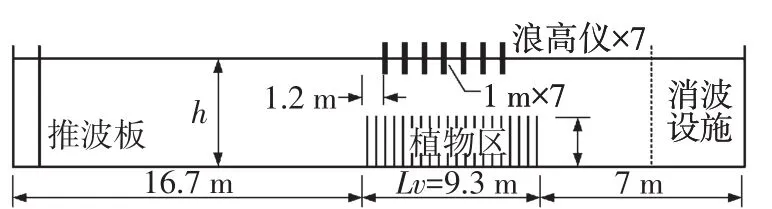
图1 Dubi试验布置简图Fig.1 Dubi′s experiment layout

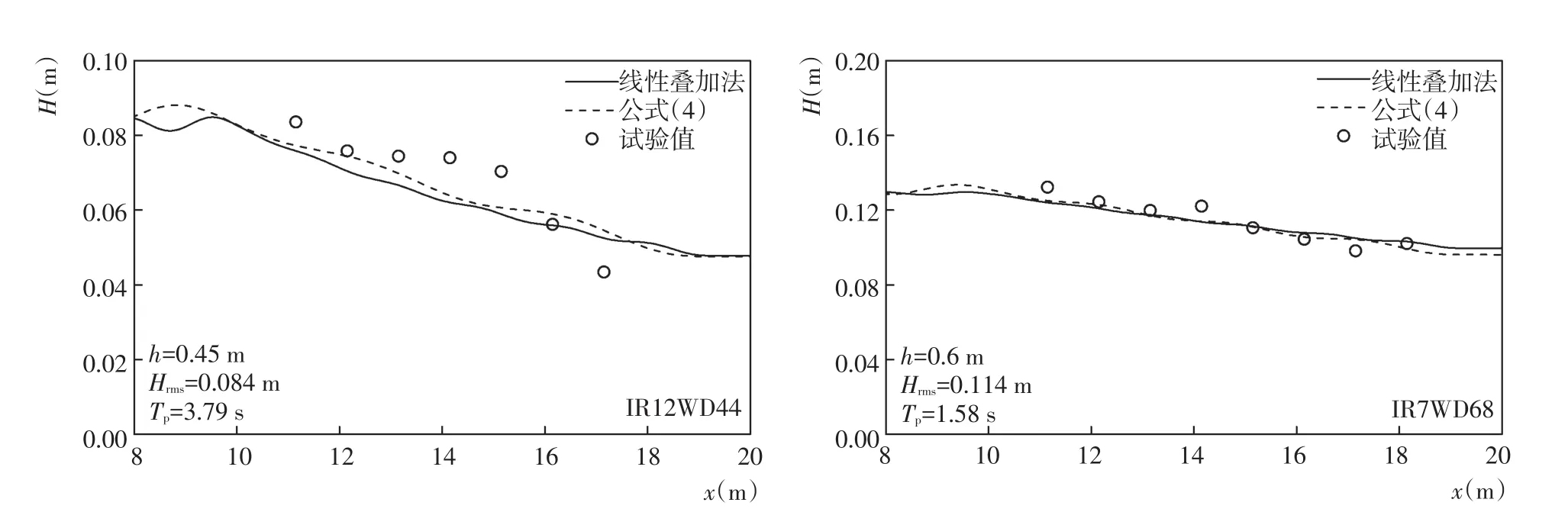
图2 Dubi试验验证结果Fig.2 Calibration results of Dubi′s experiment

这里分别采用了前文所述的线性波叠加和均方根波高表征的方法模拟随机波。线性波叠加法将随机波等能量分割成为50份分别计算。各成分波的对应的波高为Hj=4ΔS(ω̑j)Δωj，式中Hj为第 j份组成波的波高，Δωj=ωj+1-ωj，ωj为各组分波频率，代表频率ω̑j=(ωj+ωj-1)2。均方根波高表征法则采用公式（4）直接带入模型进行计算。两种方法均与物理试验吻合较好（图2）。图3给出了两组试验条件下波浪通过植物区前后的波谱衰减（由线性叠加法计算）。对比两组数值试验，发现在水深较小的算例中波浪的衰减幅度更加显著（图3）。这是由于水深较小的情况下，植物的相对淹没度（植物高度占总水深比例）较大，因而植物阻尼效应更强。对比不同频率带对应各成分波波能衰减幅度，发现低频波几乎完全被过滤，谱峰频率处衰减程度也十分明显，而高频波波能衰减幅度较小。值得注意的是这里由于模型不考虑不同频率之间的非线性作用，因此谱峰周期几乎没有变化。

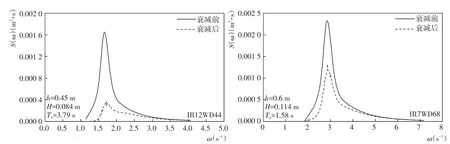
图3 植物作用下波能变化Fig.3 Energy decay caused by vegetation

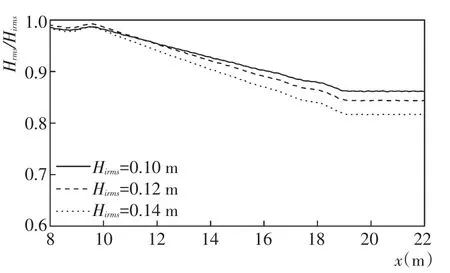
图4 不同入射波高条件下的波浪沿程衰减率HirmsHrmsFig.4 Wave height attenuation ratio HirmsHrmssimulatedwith different incident wave height conditions

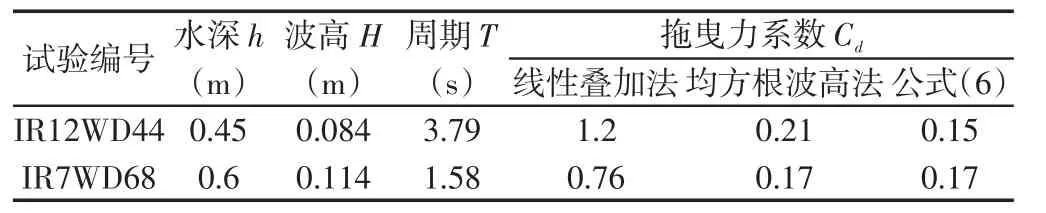
表1 不同方法求解Cd值的结果对比Tab.1 CdComparison under different numerical methods

3 拖曳力系数率定

植物消浪数值模拟的结果很大程度上取决于拖

曳力系数Cd的取值。该参数反映了植物对波浪的阻尼效应，取值受入射波高、植物种类、高度等影响［7］，在模拟中需要根据物理试验结果对其Cd取值率定。Mendez et al.［7］提出Cd与Kc（Keulegan⁃Carpenter系数）的相关经验公式

式中：参数Q=Kcα0.76，且需满足7＜Q＜172，Kc=ucTpbv，α表示植物的相对淹没度（即hvh）。为了保证参数取值的合理性，将本文率定的Cd值与公式（6）进行比较（表1）。均方根波高法率定的Cd值与公式（6）计算结果吻合良好，说明了数值模型参数取值的合理性。另一方面，采用线性叠加法率定的Cd值较公式（6）偏大，这归因于入射波高Hirms与波浪的衰减率（即HirmsHrms）之间的非线性关系。线性叠加法将波浪被线性拆分为多个成分波，从而各成分波的波高远小于原随机波的特征波高（满足波能量守恒）。因此，为了取得与有效波高法一致的计算结果，线性叠加法率定的Cd值更大。图4给出了不同入射波高条件下波浪在植物作用下的沿程衰减率（Hirms分别为0.1 m，0.12 m和0.14 m，拖曳力系数Cd取定值）。可以看出入射波高与波浪衰减率之间的非线性关系（如果两者关系为线性，则衰减率应为定值），并且入射均方根波高越小，波高的衰减率越小，即植物对波浪的阻尼作用越弱。

4 植物作用下波浪破碎

Løvås et al［5］在试验中考虑了波浪破碎的因素。试验水槽长40 m，宽0.6 m，沿程布置有10个浪高仪采集波高（图5）。试验采用波谱为JONSWAP谱，谱峰升高因子γ=3.3。为了模拟波浪破碎，水槽底部设有坡度为1：30的沙质斜坡，泥沙中值粒径D50=0.22mm，密度约为2 650 kg/m3。水槽中铺有约5 000株人工植物，植物区域长7.27 m，植物高度为0.2 m，植物密度为1 200株/m2。试验水深从0.69 m变化至0.77 m，波浪谱峰周期为2.5 s和3.5 s，入射均方根波高Hirms在0.12～0.22间变化。两组数值试验的近海端初始水深均为0.77 m。

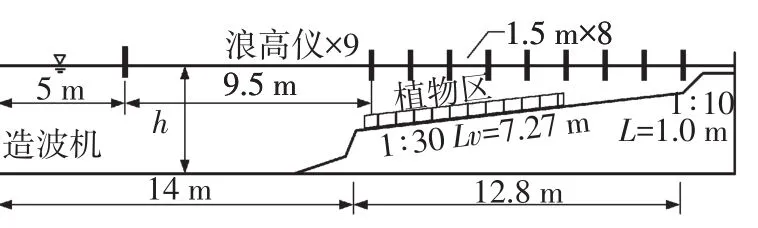
图5 Løvås et al.试验布置简图Fig.5 Løvås′s experiment layout

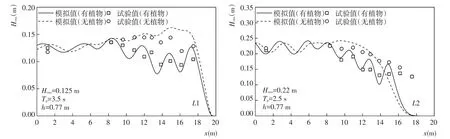
图6 波高验证结果Fig.6 Calibration results of Løvås′s experiment

模拟率定的拖曳力系数Cd与计算公式（6）所得Cd值的对比见表2，模拟结果见图6。模型可以较好的模拟出由于水下斜坡和植物共同存在而引起的波浪衰减，且模型率定的Cd值仍与公式（6）结果吻合良好，说明参数取值合理。不考虑植物作用时，波浪在传播过程中受水下斜坡的作用波高逐渐增大，直至破碎后迅速衰减。在植物的作用之下，由于浅水变形引起的波高增加被植物提供的阻力大幅削弱，波高在植物区后略微增大然后迅速破碎，破碎点的位置更接近水槽末端。需要指出模型在斜坡后端水深极小的区域模拟的波高衰减过于迅速，与物理试验相差较大。这是由于模型采用的公式（5）中εbre与水深h成-5次方，与均方根波高Hrms的7次方的关系引起的。

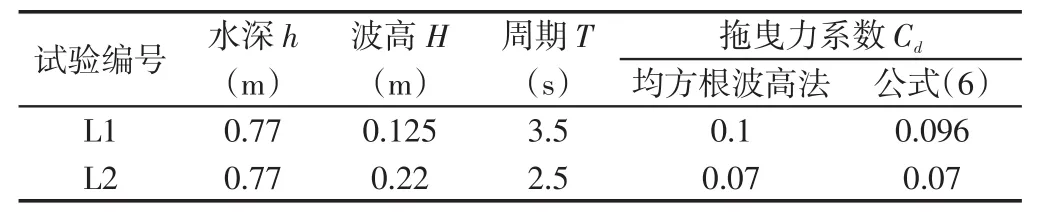
表2 不同方法求解Cd值的结果对比Tab.2 CdComparison under different numerical methods

5 结论

本文将文献［2］建立的数学模型RIDE⁃VEG拓展至可以考虑波浪的不规则性和破碎，并利用模型在合理的拖曳力系数值下对物理模型试验进行了复演，计算结果与试验数据吻合良好；分别侧重于波高的沿程衰减、波能衰减及波高的平面分布规律，针对近岸波浪在湿地植物中的传播和衰减进行研究，发现分别采用两种不同的随机波处理方式时，拖曳力系数有很大区别，采用线性叠加法的拖曳力系数大于采用公式（4）的方法，这可能是由于入射波高对于植物消浪过程的敏感性造成的；对能谱衰减的计算显示，波能在整个频域内均有衰减，衰减的幅度在谱峰周期处最大，低频处的衰减幅度大于高频处。同时考虑波浪破碎时，植物存在削弱了由于浅水变形引起的波高增大，导致波浪破碎点向岸线推进。

［1］黄本胜，赖冠文.海堤外滩地种树效果及对行洪影响［J］.人民珠江，1995（3）：38-42.

HUANG B S，LAI G W.Effects of wave protection trees growing on flood plains and its influence upon flood carry capacity［J］.Pearl River，1995（3）：38-42.

［2］才多，诸裕良.基于弱非线性RIDE模型的植物消浪数值模拟研究［J］.海洋工程，2014，32（6）：41-48. CAI D，ZHU Y L.Numerical study of vegetation⁃induced wave damping by weakly nonlinear RIDE model［J］.The Ocean Engineer⁃ing，2014，32（6）：41-48.

［3］Dalrymple R A，Kirby J T，Hwang P A.Wave diffraction due to areas of energy dissipation［J］.J.Waterway，Port，Coastal，Ocean Eng.，1984，110：67-79.

［4］Kobayashi N，Raichle A W，Asano T.Wave attenuation by vegetation［J］.Journal of Waterway，Port，Coastal，and Ocean Engineer⁃ing，1993，1（119）.

［5］Asano T，Tsutsui S，Sakai T.Wave Damping Characteristics Due to Seaweeds［C］.Japan Society of Civil Engineers（JSCE），1988.

［6］Dubi A.Damping of water waves by submerged vegetation：a case study on Laminaria Hyperborea［D］.University of Trondheim，Norway，1995.

［7］Løvås S M，Tørum A.Effect of submerged vegetation upon wave damping and run⁃up on beaches：a case study on Laminaria Hyper⁃borea［J］.Coastal Engineering，2000：851-864.

［8］Stratigaki V，Manca E，Prinos P，et al.Large⁃scale experiments on wave propagation over Posidonia oceanica［J］.Journal of Hydrau⁃lic Research，2011，S1（49）：31-43.

［9］Koftis T，Prinos P，Stratigaki V.Wave damping over artificial Posidonia oceanica meadow：A large⁃scale experimental study［J］. Coastal Engineering，2013，73：71-83.

［10］Manca E，Cáceres I，Alsina J M，et al.Wave energy and wave⁃induced flow reduction by full⁃scale model Posidonia oceanica sea⁃grass［J］.Continental Shelf Research，2012，50-51：100-116.

［11］Li C W，Zhang M L.3D modelling of hydrodynamics and mixing in a vegetation field under waves［J］.Computers&Fluids，2010，4（39）：604-614.

［12］Mendez F J，Losada I J.An empirical model to estimate the propagation of random breaking and nonbreaking waves over vegeta⁃tion fields［J］.Coastal Engineering，2004，2（51）：103-118.

［13］Ma G，Kirby J T，Su S，et al.Numerical study of turbulence and wave damping induced by vegetation canopies［J］.Coastal Engi⁃neering，2013，80：68-78.

［14］Maa J P Y，Hsu T W，Lee D Y.The RIDE model：an enhanced computer program for wave transformation［J］.Ocean Engineering，2002，11（29）：1 441-1 458.

［15］Chamberlain P G，Porter D.The modified mild⁃slope equation［J］.Journal of Fluid Mechanics，1995，1（291）：393.

［16］Kirby J T，Dalrymple R A.An approximate Model for Nonlinear Dispersion in Monochromatic Wave Propagation Models，Reply ［J］.Coastal Engineering，1987（9）：545-561.

Numerical study of vegetation⁃induced wave damping under random wave by improved RIDE⁃VEG model

CAI Duo1，XU Fan2
（1.Shanghai Water Engineering Design&Research Institute CO.,LTD.,Shanghai 200061,China;2.College of Harbor,Coastal and Offshore Engineering,Hohai University,Nanjing 210098,China）

The 2D numerical model RIDE⁃VEG was improved to simulate the vegetation⁃induced wave damp⁃ing under random wave condition,and the influences of the vegetation on wave breaking were further studied.The numerical results are in good agreement with several flume experiments.The energy spectrum analysis indicates that the wave energies over the whole frequency domain decay after passing through the vegetation region.The mag⁃nitude of the attenuation peaks at the maximum frequency,and is larger in low⁃frequency region than that in high⁃frequency region.The breaking point is closer to the coastline when considering the effects of the vegetation,which is attributed to the damping effects of the vegetation on the wave deformation in shallow water.

random wave;vegetation⁃induced wave damping;wave breaking;coast protection

U 656.31；O 242.1

A

1005-8443（2016）06-0584-05

2016-06-27；

：2016-09-07

才多（1990-），女，山东省人，硕士研究生，主要从事海岸工程及圈围工程设计工作。

Biography：CAI Duo（1990-），female,master student.