时空异常值检测的研究
2016-02-13何奇峰
何奇峰
(北京邮电大学经济管理学院,北京 海淀 100876)
时空异常值检测的研究
何奇峰
(北京邮电大学经济管理学院,北京 海淀 100876)
异常值检测是数据挖掘研究领域的一个相当重要的分支,异常值检测的目的是寻找与其他大多数对象不同的个体,又常被称为离群检测或者是例外挖掘。许多文献已经对空间异常值检测和时间序列异常值的检测进行了研究,然而同时对时间维度和空间维度进行异常值侦测的还不多;本文将分别从时间和空间这两个维度出发对异常值的检测进行研究,然后再将这两个维度结合起来,提出一种全新的时空异常值的检测方法,为未来时空异常值的检测奠定基础。
异常值检测;数据挖掘;voronoi图;k-means聚类
本文著录格式:何奇峰. 时空异常值检测的研究[J]. 软件,2016,37(12):162-165
0 引言
异常值检测是数据挖掘研究领域的一个相当重要的分支,异常值检测的目的是寻找与其他大多数对象不同的个体,又常被称为离群检测或者是例外挖掘。异常值检测在诸如金融欺诈、入侵检测、公众健康与生态环境监测预报等多个领域都取得了相当不错的应用。随着大数据时代的到来,越来越容易取得像温度,用户流量使用等时空数据,检测这类数据异常值的重要性也日益凸显。
空间异常值是指那些非时空值与周围相邻的个体显著不同的值。这表明具有空间异常值的个体是与它相邻的个体显著不同的,然而他并非与总体有显著的不同。从空间异常值可以延伸出时空异常值的概念,即时空个体具有与周围时间相邻和空间相邻个体显著不同的非时空值。
时空异常值的检测主要有三种方法:第一种是直接判定该个体是否与他时空相邻的个体的非时空值有明显的差异,第二种是时空异常值体的检测,这种时空异常值体是跨越时间的,并不像时空异常值仅仅是某一时刻的值,第三种是对时空异常值轨迹的探索。
Birant和Kut[1]提出了一个基于密度的时空异常值检测机制。他们使用了DBSCAN(具有噪声的基于密度的聚类方法)聚类算法用于对空间维度进行聚类从而识别空间异常值。DBSCAN能划分任意形状的类并且对高效的处理大数据集,然而DBSCAN并没有考虑时间维度,当不同类别密度不同时,它也不能判别出某些异常值。因此他们使用了改进的DBSCAN,具体有两点改进:一直为了支持时间维度,通过遍历一棵树找出任一个个体在一定半径范围内的时间邻居和空间邻居,二是当类别具有不同的密度时,会给每一个类分配一个密度因子,然后将新生成类的值与平均值进行比较从而发现异常值。Cheng和Li提出了一个四步法,用以处理语义和动态属性的地理现象的时空异常值检测。这四步分别是发现语义个体,聚合,对比,验证。Adam(2004)[3]研究了基于距离的时空异常值检测,根据微类的空间和语义相似性融合成巨类。运用雅各比系数和轮廓系数来计算微类的空间相似性。在巨类中任一与其他点不同数据将被标记为时空异常值。
许多文献已经对空间异常值检测和时间序列异常值的检测进行了研究,然而同时对时间维度和空间维度进行异常值侦测的还不多,有一些研究也是单纯的把时空分割开,即分别检测出时间异常值和空间异常值,最后结合这两部分来判定时空异常值。然而时间维度和空间维度是相互关联的,所以同时结合时空两个维度进行异常值的检测是很有必要的。
1 时空异常值简介
1.1 时间维度异常值检测
时空数据多以面板数据的形式存在,面板数据是在时间序列上取多个截面,在这些截面上同选取样本观测值所构成的样本数据,也就是把截面和时间序列数据融合在一起的数据集。面板数据集显示个体之间存在差异,而单独的时间序列或横截面不能有效反映这种差异,如果只是简单使用时间序列或横截面分析就可能获得有偏结果。同时面板数据能够提供更多信息、更多变化性、更少共线性、更多自由度和更高效率。

图1 滑动窗口图
时空数据通常具有数据流的特点,数据流是指连续产生的、没有边界的大量数据元素所组成的序列。为了能更好的处理数据流,本文将使用滑动窗口模型,随着新数据的到来。滑动窗口以基本窗口为单位不断更新。每进入一个新的基本窗口,最旧的一个基本窗口被删除,滑动窗口随之更新一次。因此,滑动窗口中包含的数据不断变化和更新。
1.2 空间维度异常值检测
空间离群点是与其空间邻域中其它空间对象的非空间属性值存在明显差异的空间对象。空间离群点挖掘是空间数据挖掘的一个重要分支,在交通控制、遥感图像分析、气象预报和人口统计数据分析等应用中可揭示重要现象。随着传感器设备技术的发展,数据采集设备的数量越来越多,精度越来越高,采集的项目也越来越多,因此数据量越来越大,维数越来越高。然而现有的空间离群点挖掘算法主要是针对单维或中低维的中小规模数据量的挖掘,难以适应高维大数据量的挖掘,并且现有算法没有充分考虑空间数据的特点,挖掘的不是真正意义上的空间离群点,而是全局离群点。算法存在用户依赖性大,检测精度低,挖掘效率低等局限。
考虑空间这一维度,需要对整个空间的点进行区域划分,对此本文将研究Voronoi图等能保持区域拓扑结构的模型。Voronoi图是计算几何中一种几何结构,也是一种空间分割的方法[6]。Voronoi图可以作为表示各种元素之间关系的一个结构,通过这个结构可以提取出重要信息。这样的实例多见于用Voronoi图研究自然界物质结构的性质。把Voronoi图作为一个辅助数据结构,通过这个数据结构可以完成许多物体形态或邻近关系的计算任务。把Voronoi图作为提高某些几何算法运算速度的重要手段.一般来说,二维的Voronoi图可以在O(nlogn)时间内获得,三维的Voronoi图可以在O(n2)时间内获得.Voronoi图的性质决定了它与许多其它几何结构具有内在关系,通过Voronoi图,许多几何算法可以得到快速运算。
2 时空异常值检测的结合
在空间维度上运用Voronoi 图对空间位置进行划分,重新定义了各个位置之间的距离以及相邻关系,利用重新的定义的距离对非时空值从空间维度进行限制;在时间维度上,由于时空数据多以面板数据的形式存在,面板数据是在时间序列上取多个截面,在这些截面上同选取样本观测值所构成的样本数据,也就是把截面和时间序列数据融合在一起的数据集。面板数据集显示个体之间存在差异,而单独的时间序列或横截面不能有效反映这种差异,如果只是简单使用时间序列或横截面分析就可能获得有偏结果。同时面板数据能够提供更多信息、更多变化性、更少共线性、更多自由度和更高效率。时空数据通常具有数据流的特点,数据流是指连续产生的、没有边界的大量数据元素所组成的序列。为了能更好的处理数据流,本文将使用滑动窗口模型,随着新数据的到来。滑动窗口以基本窗口为单位不断更新。每进入一个新的基本窗口,最旧的一个基本窗口被删除,滑动窗口随之更新一次。因此,滑动窗口中包含的数据不断变化和更新。
对当前的滑动窗口的非时空值使用k-means聚类[8],得到时间维度的各个分类;通过Voronoi 图重新定义的相邻关系对这个聚类结果再加以细分从而得到了时空相结合的聚类结果,根据聚类的结果将数据样本很少的类别判定为异常值,由此得到了一个滑动窗口下的异常值判定;接下来使用三次指数平滑算法进行迭代。
三次指数平滑算法可以对同时含有趋势和季节性的时间序列进行预测,该算法是基于一次指数平滑和二次指数平滑算法的。[9]
一次指数平滑算法基于以下的递推关系:

其中α是平滑参数,si是之前i个数据的平滑值,取值为[0,1],α越接近1,平滑后的值越接近当前时间的数据值,数据越不平滑,α越接近0,平滑后的值越接近前i个数据的平滑值,数据越平滑,α的值通常可以多尝试几次以达到最佳效果。
一次指数平滑算法进行预测的公式为:xi+h=si,其中i为当前最后的一个数据记录的坐标,亦即预测的时间序列为一条直线,不能反映时间序列的趋势和季节性。
二次指数平滑保留了趋势的信息,使得预测的时间序列可以包含之前数据的趋势。二次指数平滑通过添加一个新的变量t来表示平滑后的趋势:

二次指数平滑的预测公式为xi+h=si+hti二次指数平滑的预测结果是一条斜的直线。三次指数平滑在二次指数平滑的基础上保留了季节性的信息,使得其可以预测带有季节性的时间序列。三次指数平滑添加了一个新的参数p来表示平滑后的趋势。
三次指数平滑有累加和累乘两种方法,下面是累加的三次指数平滑
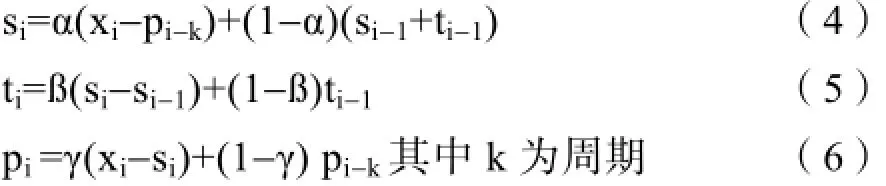
下式为累乘的三次指数平滑:

累乘三次指数平滑的预测公式为:

α,ß,γ的值都位于[0,1]之间,可以多试验几次以达到最佳效果。
S,t,p初始值的选取对于算法整体的影响不是特别大,通常的取值为s0=x0,t0=x1-x0,累加时p=0,累乘时p=1。
3 结论
本文提出了一种将时间维度和空间维度有效结合起来的异常值检测方法,在时间维度上,运用滑动窗口模型,能很好的处理数据流形式的数据,同时能很好的压缩数据的信息;在空间维度上,运动
Voronoi图对空间进行区域划分,保持空间整体的拓扑性质,同时在Voronoi图的背景下定义距离和连通性的概念,为后续联系时间维度和空间维度的研究奠定了基础。
[1] Birant, D. and Kut, A. (2006). Spatio-Temporal Outlier Detection in Large Databases. Journar of Computing and Information Technology
[2] A Multiscale Approach for Spatio-Temporal Outlier Detection. Transactions in Geographic Information Systems, 10(2): 253–263.
[3] Sun, Y., Xie, K., Ma, X., Jin, X., Pu, W., and Gao, X. (2005). Detecting Spatio-Temporal Outliers in Climate Dataset: A Method Study. In Proc. Of the 2005IEEE Intl. Geoscience and Remote Sensing Symposium, pages 760–763.
[4] Drosdowsky, W. (1993). An Analysis of Australian SeasonalRainfall Anomalies: 1950–1987. Intl. Journal of Climatology, 13(1): 1–30.
[5] Ester, M., Kriegel, H. -P., Sander, J. , and Xu, X. (1996). A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proc. Of the 2nd ACM Intl. Conf on Knowledge Discovery and Data Mining(KDD), pages 226–231.
[6] Adam, N. R., Janeja, V. P., and Atluri, V. (2004). Neighborhood Based Detection of Anomalies in High Dimensional Spatio-temporal Sensor Datasets. In Proc. of the 2004 ACM Symposium on Applied Computing, pages 576–583.
[7] Wu, E., Liu, W., and Chawla, S. (2010). Spatio-Temporal Outlier Detection in Precipitation Data. In Proc. Of the 2nd Intl. Conf. on Knowledge Discovery from Sensor Data, pages 115–133.
[8] Lu, C. -T. and Liang, L. R. (2004). Wavelet Fuzzy Classification for Detecting and Tracking Region Outliers in Meteorological Data. In Proc. Of the 12th Annual ACM Intl. Workshop on Geographic Information Systems, pages 258–265.
[9] Neill, D. B. and Cooper, G. F. (2010). A Multivariate Bayesian Scan Statistic for Early Event Detection and Characterization. Machine Learning, 79(3): 261–282.
[10] Ge, Y., Xiong, H., Zhou, Z. -h., Ozdemir, H., Yu, J., and Lee, K. C. (2010). Top-Eye: Top-K Evolving Trajectory Outlier Detection. In Proc. Of the 19th ACM Intl. Conf. on Information and Knowledge Management, pages 1733–1736.
Research on The Spatio-temporal Outlier Detection
HE Qi-feng
(School of Economics and Management, Beijing University of Post and Telecommunication, Beijing)
Outlier detection is a very important branch of data mining, the purpose of outliers detection is to find out the individuals that are different from most other objects, it is often called outlier detection or exception mining. Many literatures have studied the detection of spatial outliers and detection of temporal outliers, but there are not too many methods to connect temporal outliers and spatial outliers. This paper will research temporal outliers and spatial outliers individually, and then combine these two dimensions to propose a new detection method of spatiotemporal anomalies, which will lay a foundation for the future detection of Spatio-temporal anomalies.
Outlier detection; Data mining; Voronoi graph; K-means clustering
TP311
A
10.3969/j.issn.1003-6970.2016.12.034
何奇峰(1991-),男,硕士研究生,主要研究方向:数据挖掘
