基于改进极限学习机的MBR仿真预测研究

杨新星，李春青

(天津工业大学计算机科学与软件学院，天津 300387)

基于改进极限学习机的MBR仿真预测研究

杨新星，李春青

(天津工业大学计算机科学与软件学院，天津 300387)

研究MBR膜通量，进行膜污染预测，是当今污水处理研究领域的重要课题之一。为了有效，准确地预测MBR膜通量，提出一种改进的极限学习机( PSO-ELM)预测模型。极限学习机（ELM）能够有效地克服反向传播（BP）算法的缺陷，并能以极快的速度获得很好的泛化性能。由于随机给定输入权值和隐层阈值，ELM通常需要较多隐含层节点才能达到理想精度。利用粒子群算法（PSO）对极限学习机（ELM）的权值和阈值进行优化，建立PSO-ELM预测模型，将提取的主成分作为该模型的输入，膜通量作为模型输出。研究结果表明，该模型对MBR膜通量预测具有较好的泛化能力和更高的预测精度。

膜生物反应器；膜通量：极限学习机：粒子群算法

本文著录格式：杨新星，李春青. 基于改进极限学习机的MBR仿真预测研究[J]. 软件，2016，37（12）：17-20

0 引言

膜生物反应器（Membrane Bioreactor，MBR）是将生物降解作用与膜的高效分离技术结合而成的一种新型高效的污水处理与回用工艺[1]。使用膜分离装置取代了传统的二次沉淀池，并且较好得截留了反应池中的活性污泥以及其中的大分子有机物质。因此，与传统污水处理工艺相比，MBR具有出水水质好且稳定，能有效使固液分离，污泥产量少，并且设备紧凑、不占用大量空间等优势。然而污水处理过程中伴随着膜污染问题，严重得影响了膜的通透性能和使用寿命。膜污染直接导致的结果是膜通量的下降，所以膜通量大小可以衡量膜污染的程度[2]。所以，膜通量能否及时、准确地预测是膜污染控制的关键。

目前，智能仿真模型在MBR膜通量预测中的应用越来越受到重视。国内外学者针对影响膜污染的污泥浓度、操作参数等指标做了大量的研究，建立膜污染数学模型，通过膜通量变化情况来预测膜污染程度。但这依然存在诸多不足，比如数据信息重叠，模型结构相对复杂，收敛速度慢，泛化能力较差以及局部极小化等问题。故本文提出一种改进极限学习机的MBR膜通量预测模型。采用主成分法对影响膜通量的相关因素进行降维处理，提取其特征信息，消除向量相关性[3]，将提取的主要影响因素作为粒子群极限学习机的预测模型参数，并利用粒子群算法（PSO）优化极限学习机（ELM）参数，使得优化后的ELM模型具有更高的预测精度和更好的预测效率，再将现场实验数据带入到该模型中，验证其有效性。

1 极限学习机理论与粒子群算法

1.1 极限学习机模型

极限学习机（extreme learning machine，ELM）是由黄广斌[4]等人在2006年提出的一种基于单隐藏层前馈神经网络的新型学习方法。与传统前馈神经网络不同在于，对实验样本训练前，先设定好隐层节点数，执行过程中会自动对输入权值和阈值随机赋值，这个过程只需进行一次，无需再进行迭代，并且产生唯一最优解。因此，具有学习效率高，泛化性能好等优点。极限学习机网络结构如图1所示。

图1 极限学习机网络结构Fig.1 Network Structure of ELM

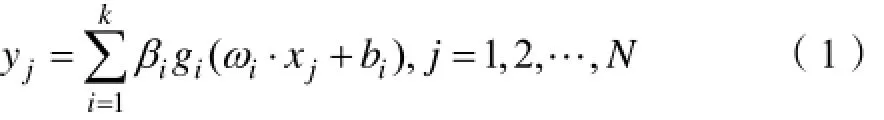
上述N个方程的矩阵形式可以表示为

式中：

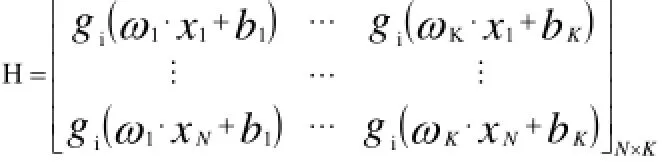
其中：H是ELM隐藏层输出矩阵；T是目标输出向量。

根据上述方程，求出最小范数二乘解。即得：

通常，选取的隐层节点数越接近样本数量时，其预测值就会越逼近期望值。但这存在隐层节点数过大和数据复共线性等问题。而复共线性问题又会导致极限学习机模型输出出现不稳定性，误差增大，拟合效果变差。

1.2 粒子群算法（PSO）

粒子群算法是由Kennedy和Eberhart[6]提出的一种优化算法。其中每个粒子都是一种可能的解，多个粒子组成群体，粒子通过不断更新速度和位置寻找最优解。在解空间中，通过记录自身的个体信息（Pbest）和群体信息（Gbest）共同决定他们飞行的方向和距离。每迭代一次粒子就产生一个适应度值，通过比较个体极值Pbest和全局极值Gbest来更新自己。

上式中，ω为惯性权重，C1和C2为学习因子，r1和r2为分布在[0,1]的随机数。为了防止粒子在寻找最优解中可能出现超出预期范围的情况，将粒子的速度信息限制在[vmin,vmax]，位置信息限制在为[xmin,xmax]。

1.3 PSO优化ELM具体步骤

由于ELM的输入权值和阈值随机给定，针对这一不足，利用PSO全局寻优的特点对ELM的权值和阈值进行优化处理。PSO优化ELM主要步骤如下：

（1）随机选取适量样本；

（2）设定模型网络拓扑结构；

（3）初始化粒子位置和粒子速度，根据权值和阈值的范围设置粒子速度和位置的寻优范围[7]；

（4）初始化算法参数。包括设置最大迭代次数为20，种群规模为200，惯性权重0.7298 ω=，加速度因子c1=c2=1.4962；

（5）通过训练样本，计算出均方根误差，并将其作为适应度值函数。再找出粒子的Pbest和Gbest；

（6）通过比较，不断更新粒子的速度和位置[8]；

（7）进行迭代，判断是否达到最大迭代次数，若不满足，则继续回到（5），直到停止迭代，最终得出最优的权值和阈值。

2 基于PSO-ELM膜通量的仿真预测模型

2.1 影响因素的确定

微生物污染、无机污染、有机污染相互交叉、互相影响，共同构成了MBR膜污染的主要类型，所以膜通量的大小受多种因素的综合影响[9-10]，主要因素有混合液污泥浓度、温度、进水压力、产水压力、校正流量、COD等。大量的实验表明，对MBR膜通量起决定作用的因素有：进水压力、产水压力、校正流量。所以，本文将以上3项作为影响MBR膜通量关键因素，建立PSO-ELM膜通量预测模型。

2.2 训练样本与测试样本的选择

本文所用实验数据来源于某MBR污水处理厂历史生产数据。将进水压力、产水压力、校正流量作为预测模型的输入参数，MBR膜通量作为预测模型的输出参数。从中随机选取其中120组数据，其中110组作为训练样本，剩余的10组作为预测样本。

2.3 预测模型参数设置

本文用PSO-ELM算法模型进行MBR膜通量预测时，其中网络的隐含层激活函数为“sigmoid”，设置粒子群初始化参数NP=200，itermax=20，C1=C2=1.4962，ω=0.7298。实验通过Matlab实现。

3 预测结果与实验结果对比及分析

由于极限学习机随机选择隐藏节点参数（权重和偏置），导致很多情况下需要更多的隐藏节点才能达到理想精度[11]。为对结果进行比较，本文采用预测值与实际值的相对误差（MRE）作为评价模型预测效果的标准。将ELM与PSO-ELM的隐藏节点数目逐渐增加，测试不同节点数目下的预测样本的平均相对误差，结果如图2所示。

ELM的预测效果相较于PSO-ELM，其预测误差随着隐层节点数的变化表现出不稳定性，当只有选择合适的隐藏节点数时，才会有较好的预测结果。过多过少的隐层节点数都会出现拟合效果不好的特点，预测误差增大。对于经过PSO优化的ELM算法，误差有了明显的改善，均低于ELM误差，而且大大简化了“无用”的神经网络节点，说明PSO-ELM能够有效减少隐藏层节点数，获得更为紧凑的网络体系结构，提升系统的稳定性。为使PSO-ELM预测误差最小，本文将隐藏节点数设置为20。

图2 预测误差随隐藏节点数的变化Fig.2 Prediction Error Changes with The Number of Hidden Nodes

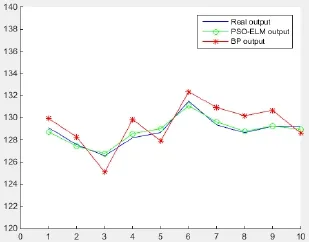
图3 预测结果对比Fig. 3 Comparison of Prediction Results

为了验证该算法的有效性，用同样的样本建立BP网络预测模型来预测MBR膜通量。将预测结果与PSO-ELM的预测结果进行比较。比较结果如图3所示。数据分析结果见表1。经PSO优化的ELM预测模型，其预测的相对误差均低于BP预测模型，平均相对误差为0.19%，最大相对误差不超过0.3%，可见经过优化后的PSO-ELM预测模型的学习能力要比BP预测模型学习能力要强，并且具有更高的预测准确度和更好的泛化性能。

表1 膜通量预测结果Tab.1 The Prediction Results of Membrane Flux

4 结论

本文将PSO-ELM方法应用于MBR膜通量预测，通过选取最优隐含层节点数，训练进水压力、产水压力、校正流量参数，建立最优ELM模型。

（1）利用主成分分析法对MBR膜通量众多影响因素进行降维处理，从而简化了模型的网络结构，减少因指标过多而带来的工作量。

（2）ELM算法克服了传统神经网络算法易陷入局部最小，泛化性能差等缺点，经PSO算法优化后，不仅大大减少了隐层节点数，而且也提高了预测精度。

（3）将经PSO优化的ELM算法应用在MBR膜通量预测模型中。用实际污水处理数据进行实验，实验取得了理想的效果，表明该改进的算法能较好的对MBR膜通量进行预测。

[1] 张颖, 张铁峰, 王爱杰,等. 膜生物反应器(MBR)技术关键及应用[J]. 东北农业大学学报, 2002, 33(1): 96-99.Zhang Y, Zhang T F, Wang A J, et al.. Technological key and application of membrane bio-reactor[J]. Journal of Northeast Agricultural University, 2002, 33(1): 96-99. (in Chinese)

[2] 闫宏英, 李春青. MBR膜污染的智能模拟预测方法研究[J].计算机测量与控制, 2013, 21(8): 1-5. Yan H Y, Li C Q. Research of intelligent simulation forecasting methods on MBR membrane fouling[J]. Computer measurement and control, 2013, 21(8): 1-5. (in Chinese)

[3] Abdi H, Williams L J. Principal component analysis[J]. Wiley Interdisciplinary Reviews Computational Statistics, 2010, 2(4): 433–459.

[4] Huang G B, Wang D H, Lan Y. Extreme learning machines: a survey[J]. International Journal of Machine Learning and Cybernetics, 2011, 2(2): 107-122.

[5] Huang G B, Zhu Q Y, Siew C –K. Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006,70(1-3): 489-501.

[6] Kennedy J, Eberhart R, Shi Y H. Swarm Intelligence[M]. San Francisco, Cal, USA: Morgan Kaufmann Publishers, 2001: 287-318.

[7] Kennedy J, Eberhart R. Particle Swarm Optimization[C]. Perth, Australia: Proceedings of IEEE International Conference on Neural Networks, 1995: 1942-1948.

[8] 郭建青, 李彦, 王洪胜,等, 粒子群优化算法在确定河流水质参数中的应用[J].水利水电科技进展, 2007, 27(6): 1-5. Guo J Q, Li Y, Wang H S, et al. Application of particle swarm optimization algorithms to determination of water quality parameters of river streams[J]. Advances in Science and Technology of Water Resource, 2007, 27(6): 1-5. (in Chinese)

[9] 韩永萍, 肖燕, 宋蕾, 王晓琳. MBR膜污染的形成及其影响因素研究进展[J]. 膜科学与技术, 2013, 01: 102-110. HAN Y P, XIAO Y, SONG L,WANG X L. Study on the factors of MBR formation and the influence of membrane fouling[J]. Membrane science and technology, 2013, 01: 102-110. (in Chinese)

[10] Howell J A. Future of membranes and membrane reactors in green technologies and for water reuse[J].Desalination, 2004, 162(1): 1-11.

[11] 王杰, 毕浩洋. 一种基于粒子群优化的极限学习机[J]. 郑州大学学报(理学版), 2013, 45(1): 100-104. Wang J, Bi H Y. A new extreme learning machine optimized by PSO[J]. Journal of Zhengzhou University: Natural Science Edition, 2013, 45(1): 100-104. (in Chinese)

Research of MBR Simulation Predictions Based on Improved Extreme Learning Machine

YANG Xinxing, LI Chunqing

(School of Computer Science and Software Technology, Tianjin Polytechnic University, Tianjin 300387, China)

MBR membrane flux research for membrane fouling prediction is one of the important topics on today's sewage treatment research field. In order to effectively and accurately predict the flux of MBR membrane, a prediction model was proposed based on improved extreme learning machine (PSO-ELM). Extreme Learning Machine could overcome the drawbacks of backpropagation algorithm with extreme learning speed and better generalization performance. ELM usually requires more hidden layer nodes to achieve the desired accuracy because of the random input weights and hidden layer threshold. Using particle swarm optimization( PSO) to optimize the input weights and hidden layer threshold of extreme learning machine ( ELM), establish PSO-ELM prediction model, treat the extractive principal components as the input of the prediction model, the membrane flux as the model output. The results show that the proposed model has better generalization ability and higher prediction precision for membrane flux.

MBR; Membrane flux; Extreme learning machine; Particle swarm optimization

TP391

A

10.3969/j.issn.1003-6970.2016.12.004

国家自然科学基金(51378350)；国家杰出青年科学基金(50808130)

杨新星(1990-)，男，硕士研究生，主要研究方向：MBR计算机模拟仿真，大数据。

李春青，教授，主要研究方向：MBR计算机模拟仿真，大数据与云计算。