基于图表示的鲁棒高效的高光谱图像波段选择方法

孙康 耿修瑞 陈金勇 计璐艳 唐海蓉 赵永超 许妙忠

1.中国电子科技集团公司第五十四研究所

2.中国科学院电子学研究所

3.清华大学地球系统科学研究中心

4.武汉大学测绘遥感信息工程国家重点实验室

技术应用

基于图表示的鲁棒高效的高光谱图像波段选择方法

孙康1耿修瑞2陈金勇1计璐艳3唐海蓉2赵永超2许妙忠4

1.中国电子科技集团公司第五十四研究所

2.中国科学院电子学研究所

3.清华大学地球系统科学研究中心

4.武汉大学测绘遥感信息工程国家重点实验室

在非监督波段选择领域，算法鲁棒性和高效性具有重要意义。本文基于图表示提出了非监督波段选择算法，称为GRBS（graph representation based band selection），该算法既对噪声波段有较高的鲁棒性，同时又具有较低的计算复杂度。在GRBS算中，高光谱波段被当作高维空间中的一个节点，这些节点聚成一些簇团，位于簇团中心的波段是GRBS选择的理想波段。有趣的是，不同于其他基于聚类的波段选择方法，GRBS并不需要对波段进行聚类分析，而是通过一个计算简单的准则函数选择目标波段，这样大大降低了计算复杂度同时提高了算法的鲁棒性。试验结果表明，GRBS具有优良的波段选择性能，在精度和速度上能够超越传统的算法。

高光谱图像，降维，特征提取，波段选择，噪声鲁邦

一、引言

高光谱遥感可以以精细的光谱分辨率对地面物体采集从可见到红外的数百个波段(Landgrebe 2002;Plaza et al.2009)。这些丰富的信息为精细的图像应用，如地物分类和识别，提供了必要的数据基础。然而，由于高光谱图像的波段之间（尤其是相邻的波段）有较大的相关性，因此高光谱数据也同时存在着很大冗余。此外，对于一些应用，如分类，波段数的增多并不一定意味着好的结果，甚至还会降低分类精度，这就是“维数灾难”(Kim and Landgrebe 1991)。另一方面，高光谱巨大的数据量对计算能力也有很高的要求。因此，数据降维对高光谱应用有重要的作用(Dópido et al.2012)。

特征提取是一种常用的降维手段，经典的特征提取方法包括主成分分析（PCA）(Jolliffe 2005)、最小噪声分离（MNF）(Green et al.1988)以及独立成分分析（ICA）(Hyvärinen,Karhunen, and Oja 2004)，其他的一些特征提取方法包括(Bruce,koger,and Li 2002;Yang,Yu,and Kuo 2010; Chang et al.2014;Kuo 2004).。这些方法从信息保持的角度来看，具有很好的效果，选出的特征也更具有区分性。但这些特征由于是原始特征的变换，因此丧失了原始光谱的物理意义。另一个降维途径是特征选择（波段选择），它从原始波段集合中根据一定的标准，选出一个满足要求波段子集(Bajcsy and Groves 2004)。相对于特征提取，波段选择的好处是，得到的特征具有物理意义。此外，波段选择对与高光谱数据获取，传输，以及储存也具有积极的意义。事实上，波段选择已经成为了高光谱预处理中的一个重要步骤。

整体上，波段选择的方法可以分为监督方式和非监督方式两大类。监督的波段选择需要一定的先验信息如训练样本和目标光谱等(Bruzzone and Serpico 2000;Kuo et al.2014; Yang et al.2011; Sun,Geng,and Ji 2014)。但是在实际中，受限于时间和经费的限制，这些先验信息往往无法获得(Bruzzone,Chi,and Marconcini 2006;Dópido et al.2012)，在这种情况下，我们需要发展一些广泛适用于不同目标或者类别的，能获得较好性能的可靠波段选择算法。也就是非监督的波段选择算法，本文重点着眼于非监督波段选择算法。

非监督的波段选择已经有了一些研究成果。有些方法是基于波段排序的(Chang et al.1999;Chang and Wang 2006)，这些方法一般先定义某个指标（一般是单波段的指标），然后对各个波段计算指标并排序并依照排序顺序选择需要的波段。如IDBS依据波段的偏离对应高斯分布的程度进行排序，ID值越大，则权重越大。尽管排序算法不需要子集搜索果，因此速度较快，但是由于没有考虑相关性，得到的波段往往相关性很大。

有些其他方法在设计代价函数时考虑了波段的相关性，比如OIF (Beauchemin and Fung 2001)和MEV (Sheffield 1985)。与基于排序的波段选择方法不同，这类方法的准则函数是针对多波段而不是单波段的。尽管这类方法在一定程度上克服波段的相关性问题，但由于涉及到组合优化问题，往往具有较高的计算复杂度。比如，来自于端元提取方法OSP(Harsanyi and Chang 1994)的 OSPBS (orthogonal subspace projection based band selection) (Du and Yang 2008)方法，使用线性预测描述单个波段和多个波段之间的相似性。它由两个最优波段组合开始，然后逐个增加波段至三、四一直到选择的波段符合需求。使用入选波段对待选波段进行线性预测，具有最大重建误差的波段作为新入选波段。由于涉及到频繁的最小二乘计算，该方法具有较高的计算复杂度。

这些基于目标函数的波段选择方法另外一个缺点是更倾向于选择外点（噪声点）而不是代表性强的波段，见图1。比如，MEV的目标是选择具有最大协方差矩阵行列式的波段组合，也即具有最大体积的波段(Geng et al.2010);constrained band selection (CBS)(Chang and Wang 2006)倾向选择偏离数据云团的波段；基于NFINDR(Winter 1999)的波段选择方法(Wang,Jia,and Zhang 2007)选择具有最大单形体体积大波段；OSP-BS选择最不相似的波段集合。如图1所示，这些波段选择方法倾向于选择外点（outliers）(图1a)，而不是代表点（exemplars）(图1b)。然而，外点可能被噪声严重污染，也有可能处于传感器的异常响应范围，因此代表点是更理想的选择目标，因为它们对各个子类具有较高的代表性。

现在有一些新的波段选择方法尝试选择处于聚类中心的波段，如(Martínez-Usó et al.2007;Ahmad et al.2011;Hedjam and Cheriet 2011;Jia et al.2012)。这些方法将波段选择为题看作波段聚类问题，比如WaLuMI(Ward's Linkage strategy using Mutual Information)(Martínez-Usó et al.2007)基于层次聚类，按最小类内方差和最大类间方差对波段进行聚类。尽管这些基于聚类的波段选择方法对外点有一定的鲁棒性，但仍有对噪声敏感、计算复杂度高度的缺点。

本文提出了一个新波段选择方法GRBS，该方法将基于准则函数的波段选择方法和基于聚类的波段选择方法结合起来，具有以下特点：①在不进行噪声估计的情况下，自动去除噪声波段；②对外点鲁棒；③计算复杂度低。GRBS将波段视为高维空间中图的节点（也称顶点），在该空间中波段选择问题可以作为聚类问题处理(Mitra,Murthy,and Pal 2002)。有趣的是，GRBS并不真正对波段聚类，而是通过一个新定义的准则函数选择代表波段。

二、GRBS

本节详细介绍GRBS的原理，包括准则函数和搜索策略，同时对GRBS的计算复杂度也进行了理论分析。

2.1 准则函数

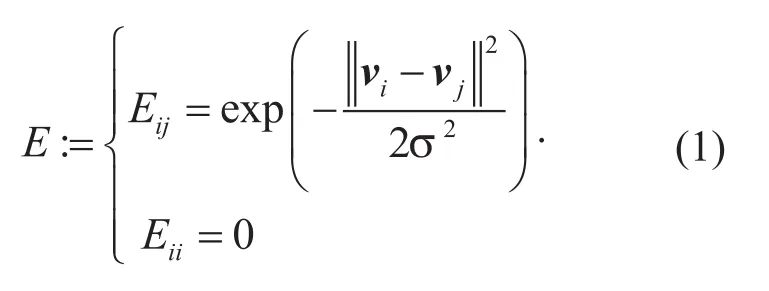
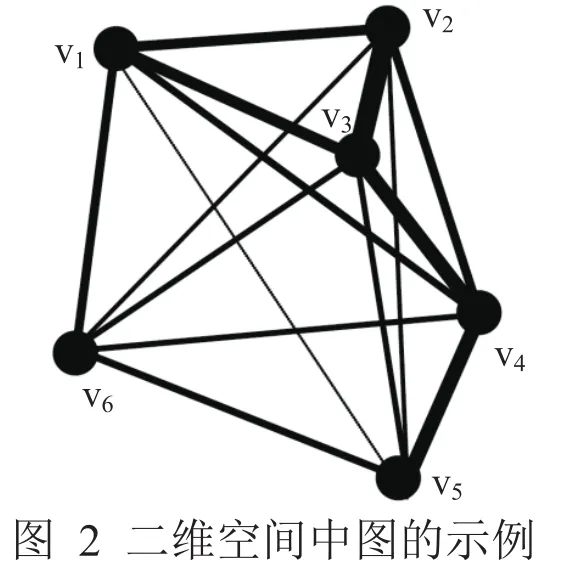
根据式（1），如图2所示的图的邻接矩阵为：

邻接矩阵的行（列）的和成为度，度是图论中一个很重要的概念。在本例中，度如下所示：

可以看出，节点的度越大，则其越靠近图的中心，反之，则偏离中心越远。比如，具有最大的度11，该点确实最靠近中心，而的度最小，该节点偏离中心最大。因此度可以用来描述节点成为代表点（中心）的可能性，或者是对类的代表程度。显而易见，如果相似的两个波段具有相似的度，但只需要他们中的一个。从式（1）中可以看出，如果某些节点之间相关性较小（距离较远），则这些节点之间的边的权重会较低，因此一个波段集合中的相关性可以使用邻接矩阵的总权重进行衡量。

GRBS需要这样的波段，每个波段都具有较大的度，并且这些波段之间的边具有较低的权重。GRBS的具体指标我们是这样定义的，使选择波段的度的和与这些波段之间的边的权重的和的比值尽量大，如下所示：

从式（4）可以看出，波段的度尽量大是要使选择的波段尽量往数据的中心靠近，而较低的波段之间边的权重（相关性抑制），是要使选择的波段尽量远离。这样这两个指标就相当于内力和外力，一个是选择倾向于数据中心的波段，一个倾向于外围的波段。通过试验可以发现，这两个力的平衡可以有效的选择鲁棒性强的波段。

2.2 关于准则函数的进一步讨论

从式（4）中可以发现，邻接矩阵对波段选择的结果起到决定性作用。本文发现如果使用欧式距离按（1）式构造邻接矩阵，则噪声波段可能没有得到充分抑制。比如，当噪声波段的亮度比较低时，噪声波段之间的欧式距离也会比较小，从而导致不合理的较大的度。另一方面，当信噪比较高的波段具有较大亮度时，也可能具有较小的度。为此本文在计算邻接矩阵前对波段归一化，公式推导如下，将（1）式重写为：

去除每个波段的亮度（模），可以得到：

关于式（6）的进一步说明如下：由于噪声之间是有极低的相关性，因此噪声波段（或者信噪比较低的波段）与其他波段之间的相关性较小。从（6）式可以看出，这些波段之间的权重较小，因而这些波段的度也越小。而高信噪比的波段，与其他波段相关性较强，因而具有较大的度。这样通过使用（6）式计算的邻接矩阵可以将噪声较大的波段排斥在图的外部，将有代表性的波段聚到图的中心，使用（4）式选择的波段就是信噪比高、更为鲁棒的波段了。

2.3 子集搜索

如何找出具有最优代价函数的波段组合对高光谱图像来说是波段选择中的另一个难题，因为这是一个NP困难问题。尽管Narendra and Fukunaga (Narendra and Fukunaga 1977)提出了快速的子集搜索算法，但只适应于单调的目标函数。对于其他目标函数，最优搜索算法只能是穷举法，对于一般拥有上百个波段的高光谱数据来说，这样计算量是不可能完成的(Serpico and Bruzzone 2001)。因此，我们需要在搜索效率与效果之间进行一次折中。幸运的是，关于如何进行这样的折中已经有了很多的方法，如 (Whitney 1971;Tsymbal,Pechenizkiy,and Cunningham 2005;Serpico and Bruzzone 2001;Pudil,Novovičová,and Kittler 1994;Narendra and Fukunaga 1977;Marill and Green 1963;Jain and Zongker 1997)，其中较为经典和常用的是序贯前向搜索法(SFS)(Whitney 1971)和序贯后向搜索法(SBS)(Marill and Green 1963)。

SFS和SBS方法都属于贪婪搜索方法。前向法是一种自下而上的搜索算法，它从较少的波段组合（如一个或两个）开始，逐个增加波段，使得增加之后的波段集合具有最优的代价函数。后向法与之相反，是一种自上而下的搜索算法，它从全部波段集合开始，逐个删除波段，使得保留波段集合具有最优的代价函数。由于高光谱波段选择问题中，一般总的波段数远远大于选择的波段数，因此一般认为后向法的计算复杂度大于前向法。为表示方便，将使用前向搜索和后向搜索的GRBS算法分别记为FGRBS和BGRBS。

2.4 计算复杂度分析

计算复杂度是波段选择中的一个重要问题，因为其重要目的之一是降低计算量。有些文献专门研究了降低波段选择计算时间的方法如Yang等(Yang,Du,and Chen 2011)提出使用GPU对波段选择进行加速。本节对GRBS的计算复杂度进行理论分析，对于GRBS，首先需要计算图的邻接矩阵。对于L波段N像元的图像，所需要的浮点操作次数约为，与计算协方差矩阵的相同。然后是波段子集搜索过程，根据（4）式，可以发现，当选择波段数为n时，前向法FGRBS所需的搜索复杂度为，而后向法BGRBS的复杂度为。由于，因此两个搜索版本的GRBS的计算复杂度均为。

三、试验验证

本节在两个由AVIRIS获取的真实数据的基础上，设计试验对GRBS的性能进行验证。三个波段选择方法IDBS(Chang and Wang 2006)，OSP-BS (Du and Yang 2008)以及WaLuMI (Archibald and Fann 2007)分别代表基于排序、基于准则函数和基于聚类的波段选择方法作为对照。试验主要研究GRBS波段选择的计算效率和计算精度。精度评价采用SVM(Melgani and Bruzzone 2004)分类的精度作为评价指标。试验使用的计算机配置为Intel Core i5-2400 3.10GHz处理器，2GB内存，软件环境为Windows XP Professional Service Pack 3操作系统以及Matlab 7.10编译环境.

3.1 Indian Pines数据

数据共有220个波段（4个无效波段已被去除），空间大小为145×145像素，图3（a）所示。该数据由于具有详细的地面调查以及免费使用，在遥感试验中使用非常广泛，根据地面调查（如图3 b所示），共有17中地物类型（其中16中为确定种类，1种为未知种类）。一般情况下，噪声波段（1-3,103-112,148-165和217-220）应该手工去除(Martínez-Usó et al.2007;Wang,Jia,and Zhang 2007)，但在本实验中，这些波段故意保留用以测试波段选择方法对噪声的鲁棒性。

精度试验

同(Jia et al.2012)一致，本文从220个中选择15个波段，各个方法波段选择的结果如见表1。

从表1中可以看出，FGRBS和BGRBS成功的将噪声波段排除，选择的波段相关性也较低（波段之间彼此不相邻），这是由于GRBS的准则函数抑制了具有较小的度（噪声波段）和较高相关性的波段（会导致较大的分母）。IDBS从原理上来说会倾向于信噪比较高的波段，但是由于是排序算法，得到的波段往往相关性很强（得到的波段有扎堆现象）。OSPBS选择了一个噪声波段，但其选出的波段很靠前（1-100内），这是因为该数据中前面的波段具有较大的模而后面的波段的模较小（如图5所示）。容易验证，如果噪声波段具有较大的模，那么这些噪声波段会被选入。WaLuMI被噪声严重影响，选择了9个噪声波段，这是因为噪声波段之间具有较低的相似性，而WaLuMI正是根据相似进行波段选择。

为了定量的比较这些方法，本文使用这些方法选出的波段进行SVM分类，将分类精度作为衡量准确性的依据。我们使用这些方法分别选出了10-50个不同数目的波段，然后使用20%的随机训练样本进行SVM分类，得到的分类精度图如图6（a）所示，另外我们还比较了在选择15个波段的情况下，SVM分类精度随着训练样本比例的关系。训练样本比例从10%变化到50%，都是使用ENVI的工具随机选取的，结果如图6（b）所示。

从图6（a）中可以看出，本文提出的两个基于GRBS的波段选择方法FGRBS和BGRBS选择的波段具有最高的分类精度，其中前向选择的波段好于后向选择的波段。另外可以看出，波段数增多并不意味着分类精度的提高。如BGRBS在选择40波段时具有最高分类精度(75.3%)，而WaLuMI在选择30个波段时，达到最高精度 (66.52%)。

整体上来看，这些方法从10个波段增加到20个波段时，精度提高最明显，而大于20个波段时，分类精度变化较小。此外，IDBS的分类精度随着波段数的增加而迅速提高。波段数较多时（＞30）甚至超过OSP-BS和WaLuMI。

从图6 (b)可以看出，当训练样本比例增多时，所有方法的分类精度都有所提高。整体上分类精度，两个基于GRBS方法获得的精度高于其他方法。同时也能看出，训练样本对算法性能评价有一定的影响，比如当训练样本为10%时，BGRBS具有最高的分类精度，而当训练样本为40%时，FGRBS具有最高的分类精度。

计算效率

这些方法在计算时间如图7所示，从图7中可以发现，从上计算时间上看，FGRBS＜BGRBS＜IDBS＜OSPBS＜WaLuMI。其中，FGRBS所用的计算时间最少，在（0.087s-0.091s）之间，随着选择波段数的增加而略有上升。BGRBS（0.127s-0.125s）的计算时间随着波段数目的增加而有所下降，这是由于采用SBS搜索策略导致的。IDBS是波段排序算法，其计算时间与选择波段无关，平均时间为0.352s.OSPBS（1.192s-5.3653s）为前选择向算法，计算时间随着选择波段数的增加呈线性增加。基于聚类的WaLuMI由于需要对波段进行聚类分析，非常耗时(21s-22s)。

3.2 Salinas数据

为进一步评估GRBS方法的性能，本文使用Salinas数据设计了一些试验。该数据包含224个波段，大小为512×217像素，根据地面真值，该地区包含16个地物类型，包括植被、裸土以及葡萄园等。真彩色合成图和地面真值分如图8所示。

噪声试验

本节中，使用全波段数据（FB）和噪声波段去除数据（NBR）的对比来研究噪声波段对不同方法的影响。在NBR数据中，手动去除噪声波段和水汽吸收波段（1-3,106-114,150-167和221-224），因此包含194个波段。利用这五种方法分别从FB数据和NBR数据选出一系列不同数目（从10到60）的波段。然后对选出波段进行SVM分类，训练样本比例为10%随机选取，得到的整体分类精度分别为图9和图10所示。

从FB数据的结果（图9）可以看出，FGRBS和BGRBS性能十分接近，并且都由于其他波段方法，如果仔细比较（图9b），FGRBS比BGRBS的分类精度稍高。基于准则函数的方法OSP-BS比WaLuMI和IDBS具有更高的分类精度，而IDBS在所有不同的波段数目下都具有最低的分类精度。

从NBR数据的结果（图10）可以看出，FGRBS和BGRBS性能仍然接近，并且都优于其他方法。有趣的是，与FB数据相比，FGRBS和BGRBS的在NBR数据的结果并没有明显的不同。这说明这两个方法对噪声有较高的鲁棒性，因为噪声去除与否并未影响它们的结果。而其他方法，特别是WaLuMI，在噪声去除之后，分类精度有大幅提高，说明这些方法对噪声波段较为敏感。对NBR数据，WaLuMI精度优于OSP-BS和IDBS。这是因为，WaLuMI倾向于选择可靠的代表波段，而OSP-BS倾向于选择外点。从NBR数据可以看出代表波段对分类而言是更佳的选择。IDBS的分类精度始终最低，主要原因是因为该方法是基于波段排序的方法，选出的波段具有较高的相关性。另一个可能的原因是该方法的非高斯性准则并不适合于分类应用(Archibald and Fann 2007)。

需要说明的是，对FB数据，OSP-BS比WaLuMI获得了更高的精度，但不能说明外点更适合分类。这是因为WaLuMI被噪声严重影响（Indian Pins数据验证了该点），而OSP-BS仅选择了少数噪声波段。本文提出的GRBS方法结合了基于准则函数的方法和基于聚类的方法，在选择代表波段的同时可以自动去除噪声波段，因此GRBS选择的波段能够获得较高的分类精度。

计算时间

GRBS的另一个优势是具有较低的计算复杂度，各方法从Salinas NBR数据中选择15个波段所用的计算时间见表2。可以看出，本文提出的FGRBS和BGRBS的计算时间比其他方法少得多，并且这两个方法的计算时间十分接近。此外，FGRBS和BGRBS的计算时间与选择波段数目无关，因为邻接矩阵的计算占据整个波段选择的绝大部分时间（约0.4s）。

四、结论

本文提出了一个具有噪声鲁棒、低计算复杂度的非监督波段选择方法GRBS。与传统波段选择方法不同，GRBS波段选择的目标是处理聚类中心的波段。有趣的是，GRBS无需对波段进行聚类，而是将波段视为高维图的节点，并且通过邻接矩阵进行波段选择，因而具有极低的计算复杂度。真实数据试验表明GRBS在精度、鲁棒性和计算效率方面都由于参与比较的方法。

此外，邻接矩阵中的调整参数 对平衡算法的鲁棒性和相关性起到关键作用。本文给出了 的经验取值，尽管该值对不同的数据有良好的适应性，如何自动化确定 的取值是未来的研究重点。

Ahmad,Muhammad,Ihsan Ul Haq,Qaisar Mushtaq,and Muhammad Sohaib. 2011."A new Statistical approach for band clustering and band selection using K-means clustering."IACSIT International Journal of Engineering and Technology 3 (6)∶606-14.

Archibald,Rick,and George Fann.2007."Feature selection and classification of hyperspectral images with support vector machines."Geoscience and Remote Sensing Letters,IEEE 4 (4)∶674-7.doi∶10.1109/LGRS.2007.905116.

Bajcsy,Peter,and Peter Groves.2004."Methodology for hyperspectral band selection."Photogrammetric engineering and remote sensing 70 (7)∶793-802.

Beauchemin,M.,and Ko B.Fung.2001."On Statistical Band Selection for Image Visualization."Photogrammetric engineering and remote sensing 67 (5)∶571-4.

Belkin,Mikhail,and Partha Niyogi.2001."Laplacian eigenmaps and spectral techniques for embedding and clustering."In Conference on Neural Information Processing Systems (NIPS),585-91.

Bruce,Lori Mann,Cliff H.koger,and Jiang Li.2002."Dimensionality reduction of hyperspectral data using discrete wavelet transform feature extraction."Geoscience and Remote Sensing,IEEE transactions on 40 (10)∶2331-8.doi∶10.1109/ TGRS.2002.804721.

Bruzzone,Lorenzo,Mingmin Chi,and Mattia Marconcini.2006."A novel transductive SVM for the semisupervised classification of remote sensing images."Geoscience and Remote Sensing,IEEE transactions on 44 (11)∶3363-73.doi∶10.1109/TGRS.2006.877950.

Bruzzone,Lorenzo,and Sebastiano B Serpico.2000."A technique for feature selection in multiclass problems."International Journal of Remote Sensing 21 (3)∶549-63.

Chang,Chein-I,Qian Du,Tzu-Lung Sun,and Mark LG Althouse.1999."A joint band prioritization and band-decorrelation approach to band selection for hyperspectral image classification." Geoscience and Remote Sensing,IEEE transactions on 37 (6)∶2631-41.

Chang,Chein-I,and Su Wang.2006."Constrained band selectionfor hyperspectral imagery."Geoscience and Remote Sensing,IEEE transactions on 44 (6)∶1575-85.doi∶10.1109/TGRS.2006.864389.

Chang,Yang-Lang,Jin-Nan Liu,Chin-Chuan Han,and Ying-Nong Chen.2014."Hyperspectral Image Classification Using Nearest Feature Line Embedding Approach."Geoscience and Remote Sensing,IEEE transactions on 52 (1)∶278-87.doi∶10.1109/ TGRS.2013.2238635.

Dópido,Inmaculada,Alberto Villa,Antonio Plaza,and Paolo Gamba.2012."A quantitative and comparative assessment of unmixing-based feature extraction techniques for hyperspectral image classification."Selected Topics in Applied Earth Observations and Remote Sensing, IEEE Journal of 5 (2)∶421-35. doi∶10.1109/JSTARS.2011.2176721.

Du,Qian,and He Yang. 2008."Similarity-based unsupervised band selection for hyperspectral image analysis."Geoscience and Remote Sensing Letters,IEEE 5 (4)∶564-8.doi∶10.1109/ LGRS.2008.2000619.

Geng,Xiurui,Yongchao Zhao,Fuxiang Wang,and Peng Gong.2010."A new volume formula for a simplex and its application to endmember extraction for hyperspectral image analysis." International Journal of Remote Sensing 31 (4)∶1027-35.

Green,Andrew A.,Mark Berman,Paul Switzer,and Maurice D.Craig.1988."A transformation for ordering multispectral data in terms of image quality with implications for noise removal." IEEE transactions on Geoscience and Remote Sensing 26 (1)∶65-74. Harsanyi,Joseph C,and Chein-I Chang. 1994."Hyperspectral image classification and dimensionality reduction∶an orthogonal subspace projection approach."Geoscience and Remote Sensing, IEEE transactions on 32 (4)∶779-85.

Hedjam,Rachid,and Mohamed Cheriet.2011."Hyperspectral band selection based on graph clustering."In Information Sciences, Signal Processing and their Applications,11th International Conference on,813-7.

Hyvärinen,Aapo,Juha Karhunen,and Erkki Oja.2004. Independent component analysis.Vol.46.New York∶John Wiley & Sons."Indian Pines data sets."ftp∶//ftp.ecn.purdue.edu/biehl/ MultiSpec/92AV3C.tif.zip(original files) and ftp∶//ftp.ecn. purdue.edu/biehl/MultiSpec/ThyFiles.zip(ground truth).

Jain,Anil,and Douglas Zongker.1997."Feature selection∶Evaluation,application,and small sample performance."Pattern Analysis and Machine Intelligence,IEEE Transactions on 19 (2)∶153-8.

Jia,Sen,Zhen Ji,Yuntao Qian,and Linlin Shen.2012."Unsupervised band selection for hyperspectral imagery classification without manual band removal."Selected Topics in Applied Earth Observations and Remote Sensing, IEEE Journal of 5 (2)∶531-43. doi∶10.1109/JSTARS.2012.2187434.

Jolliffe,Ian.2005.Principal component analysis.New York∶Wiley Online Library.

Kim,Byungyong,and David A Landgrebe.1991."Hierarchical classifier design in high-dimensional numerous class cases." Geoscience and Remote Sensing,IEEE transactions on 29 (4)∶518-28.

Kuo,Bor-Chen.2004."Nonparametric weighted feature extraction for classification."Geoscience and Remote Sensing, IEEE transactions on 42 (5)∶1096-105.doi∶10.1109/TGRS.2004.825578.

Kuo,Bor-Chen,Hsin-Hua Ho,Cheng-Hsuan Li,Chih-Cheng Hung, and Jin-Shiuh Taur.2014."A Kernel-Based Feature Selection Method for SVM With RBF Kernel for Hyperspectral Image Classification."Selected Topics in Applied Earth Observations and Remote Sensing,IEEE Journal of 7 (2)∶317-26.doi∶10.1109/ JSTARS.2013.2262926.

Landgrebe,David.2002."Hyperspectral Image Data Analysis." Signal Processing Magzine, IEEE 19 (1)∶17-28.

Marill,Thomas,and David M Green.1963."On the effectiveness of receptors in recognition systems."information Theory, IEEE Transactions on 9 (1)∶11-7.

Martínez-Usó,Adolfo,Filiberto Pla,José Martínez Sotoca,and Pedro García-Sevilla.2007."Clustering-based hyperspectral band selection using information measures."Geoscience and Remote Sensing,IEEE transactions on 45 (12)∶4158-71.doi∶10.1109/ TGRS.2007.904951.

Melgani,Farid,and Lorenzo Bruzzone.2004."Classification of hyperspectral remote sensing images with support vector machines."Geoscience and Remote Sensing,IEEE transactions on 42 (8)∶1778-90.

Mitra,Pabitra,CA Murthy,and Sankar K.Pal.2002."Unsupervised feature selection using feature similarity."Pattern Analysis and Machine Intelligence,IEEE Transactions on 24 (3)∶301-12.

Narendra,Patrenahalli M.,and Keinosuke Fukunaga.1977."A branch and bound algorithm for feature subset selection."Computers,IEEE Transactions on 100 (9)∶917-22.

Plaza,Antonio,Jon Atli Benediktsson,Joseph W Boardman,Jason Brazile,Lorenzo Bruzzone,Gustavo Camps-Valls,Jocelyn Chanussot, Mathieu Fauvel,Paolo Gamba,and Anthony Gualtieri.2009."Recent advances in techniques for hyperspectral image processing." Remote Sensing of Environment 113∶S110-S22.

Pudil,Pavel,Jana Jana Novovičová,and Josef Kittler.1994."Floating search methods in feature selection."Pattern recognition letters 15 (11)∶1119-25.

Serpico,Sebastiano B,and Lorenzo Bruzzone.2001."A new search algorithm for feature selection in hyperspectral remote sensing images."Geoscience and Remote Sensing,IEEE transactions on 39 (7)∶1360-7.

Sheffield,Charles.1985."Selecting Band Combinations from Multispectral Data."Photogrammetric engineering and remote sensing 51 (6)∶681-7.

Sun,Kang,Xiurui Geng,and Luyan Ji.2014."A band selection approach for small target detection based on CEM." International Journal of Remote Sensing 35 (13)∶4589-600.doi∶10 .1080/2150704X.2014.930196.

Tsymbal,Alexey,Mykola Pechenizkiy,and Pádraig Cunningham.2005."Diversity in search strategies for ensemble feature selection."Information fusion 6 (1)∶83-98.doi∶10.1016/ j.inffus.2004.04.003.

Von Luxburg,Ulrike.2007."A tutorial on spectral clustering." Statistics and computing 17 (4)∶395-416.

Wang,Liguo,Xiuping Jia,and Ye Zhang.2007."A novel geometrybased feature-selection technique for hyperspectral imagery." Geoscience and Remote Sensing Letters,IEEE 4 (1)∶171-5.doi∶10.1109/LGRS.2006.887142.

Whitney,A Wayne.1971."A direct method of nonparametric measurement selection."Computers,IEEE Transactions on 100 (9)∶1100-3.

Winter,Michael E.1999."N-FINDR∶an algorithm for fast autonomous spectral end-member determination in hyperspectral data."In SPIE's International Symposium on Optical Science,Engineering, and Instrumentation,266-75.International Society for Optics and Photonics.

Yang,He,Qian Du,and Genshe Chen.2011."Unsupervised hyperspectral band selection using graphics processing units."Selected Topics in Applied Earth Observations and Remote Sensing,IEEE Journal of 4 (3)∶660-8.doi∶10.1109/ JSTARS.2011.2120598.

Yang,He,Qian Du,Hongjun Su,and Yehua Sheng.2011."An efficient method for supervised hyperspectral band selection." Geoscience and Remote Sensing Letters,IEEE 8 (1)∶138-42.doi∶10.1109/LGRS.2010.2053516.

Yang,Jinn-Min,Pao-Ta Yu,and Bor-Chen Kuo.2010."A nonparametric feature extraction and its application to nearest neighbor classification for hyperspectral image data."Geoscience and Remote Sensing, IEEE transactions on 48 (3)∶1279-93. doi∶10.1109/TGRS.2009.2031812.