致密油藏重复压裂前应力场分布研究

孙元伟

(中国石油大学胜利学院油气工程学院,山东东营257061)

致密油藏重复压裂前应力场分布研究

孙元伟

(中国石油大学胜利学院油气工程学院,山东东营257061)

重复压裂技术是致密油藏增产增效的重要技术,其关键在于确定再次压裂时裂缝的重新定向,研究人工裂缝附近应力场分布至关重要。基于人工裂缝诱导应力和流体产出对原地应力场的影响,建立流固耦合离散模型和井眼-裂缝有限元力学模型,并利用FEPG开发软件对模型进行求解,定量分析致密油藏重复压裂前应力场分布情况。研究结果表明:人工裂缝附近会形成椭圆形压降区域,从生产边界到人工裂缝孔隙压力递减;平行裂缝方向裂缝影响的压降范围要小于垂直方向,并且裂缝影响范围仅略大于半缝长;裂缝附近致密储层有效应力要大于其他区域,平行裂缝方向有效应力整体上要大于垂直方向,并且在垂直裂缝方向出现了拉压应力变换区域。

致密油藏;重复压裂;流固耦合;孔隙压力;有效应力

随着中国石油勘探和开发的深入,致密油藏的重要性得到提高,在中国油气开发中占重要地位[1]。致密油藏渗透率低、渗流阻力大,须进行压裂改造,实现高产稳产、提高采油效率的目的[2]。在初次压裂后,由于致密油藏自身的特点,初次人工裂缝容易失效[3],须进行重复压裂,以提高油藏的产量;但是初次压裂后的人工裂缝及生产活动会影响原地应力的大小和方向[4]。人工裂缝对原地应力产生诱导应力场,而致密油产出影响储层孔隙压力,它们都会对原地应力产生影响,改变井眼附近的地应力分布[5],这无疑会对裂缝方位和形态产生影响,进而影响重复压裂后裂缝的定向。因此,须定量地分析人工裂缝和流体产出对井眼附近储层地应力分布的影响,从而为重复压裂裂缝定向提供依据,最终达到增产稳产的目的。由于现有的流固耦合方程太过复杂,无助于分析人工裂缝对井眼周围原地应力场的影响[6-7],须对模型进行处理。因此,笔者对多孔介质流固耦合模型进行离散化处理,考虑人工裂缝诱导应力及其对附近原地应力场的影响,建立致密油藏重复压裂前裂缝转向应力场分布有限元模型,并利用FEPG开发软件对模型进行求解,定量分析致密油藏重复压裂前应力场分布情况及其影响因素。

1 流固耦合模型建立

1.1 应力场方程

固相连续性方程[8]可表示为

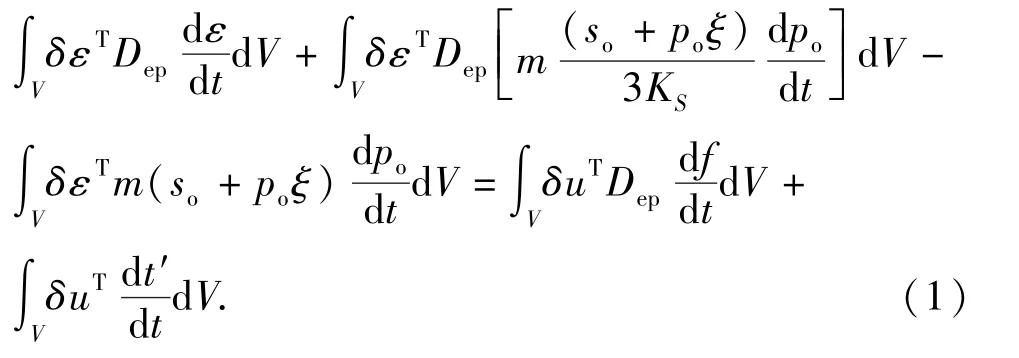
式中,ε为应变;u为位移,m;Dep为弹塑性矩阵;ξ为饱和度变化率;δ为Kronecker符号;f为体力,N/m3;V为体积,m3;S为面积,m2;so为饱和度;m为质量,kg;t为时间,s;t忆为时间变化率,s-1;po为液相压力,Pa。

将(1)式进行有限元离散可得:

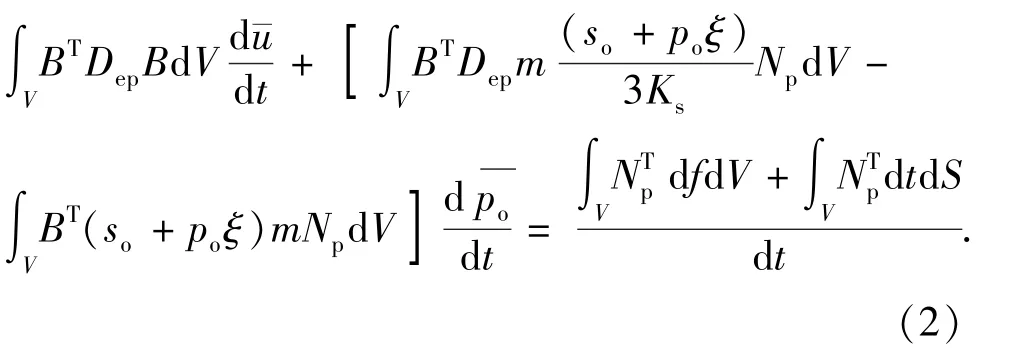
式中,B为刚度矩阵;Np为位移场的插值函数;Ks为压缩模量,GPa。

1.2 渗流场方程

渗流场连续性方程[9]为

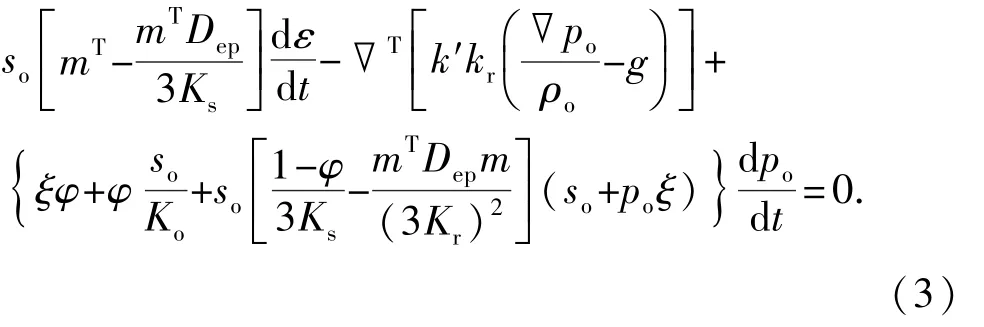
式中,φ为孔隙度,%;ρo为流体密度,g/cm3;Ko为体积模量,GPa;kr为比例渗透系数。

用Galerkin方法将式(3)有限元离散可得:

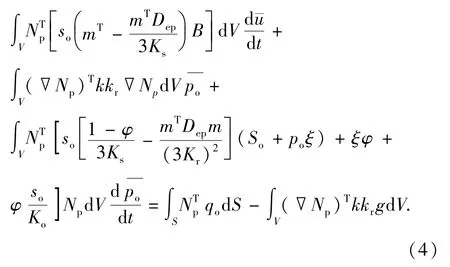
由式(2)、(4)可得流固耦合方程的简化形式:

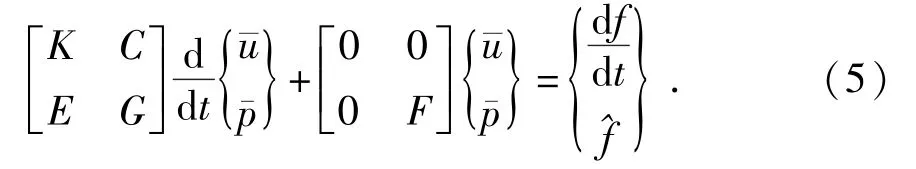
2 有限元模型的建立

在上述流固耦合模型基础上,建立了对称双翼缝的有限元力学模型,利用FEPG软件定量分析了长庆某致密油藏压裂生产一段时间后人工裂缝附近应力场分布情况,为重复压裂施工做好准备。致密储层力学参数如下:裂缝半长为30.0 m,弹性模量为5.0 GPa,泊松比为0.35,Biot系数为1.0,井眼压力为5.0 MPa,最小水平主应力为24.75 MPa,最大水平主应力为32.25 MPa,地层流体压力为15.0 MPa,初始渗透率为10×10-3μm2,地层流体黏度为200 mPa·s。

采用三角形单元,对井眼及人工裂缝附近地层进行网格加密,井眼和裂缝有限元模型见图1、2。

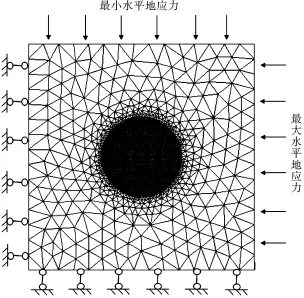
图1 有限元力学模型

图2 人工裂缝处网格加密

3 实例分析

3.1 地层孔隙压力变化规律

人工裂缝和生产时间是致密油藏储层孔隙压力变化的主要影响因素,为了宏观分析它们对井眼周围储层孔隙压力的影响,做孔隙压力云图,见图3。

由图3可知,人工裂缝周围形成椭圆形压降区域,孔隙压力从边界向裂缝呈递减分布;随着生产时间增加,压降区域向四周扩展,渐渐趋向于圆形。

图3 裂缝附近地层孔隙压力云图

3.1.1 人工裂缝

分别从平行裂缝和垂直裂缝方向分析了一定生产时间后人工裂缝对于致密油藏孔隙压力的影响,如图4所示。

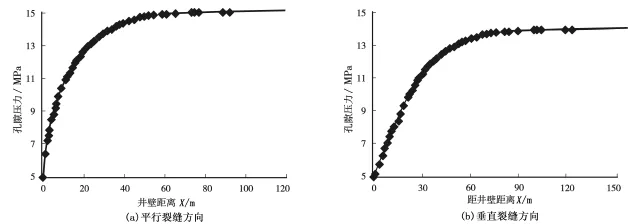
图4 孔隙压力变化曲线(t=100 d)

由图4可知,由于致密油的产出,储层孔隙压力大幅降低,并且离井眼越近变化幅度越大,在较远处基本保持恒定;与平行裂缝方向相比,在垂直裂缝方向上人工裂缝对孔隙压力的影响范围更大一些,影响范围约为60 m,与半缝长接近。

3.1.2 生产时间

选取垂直裂缝面方向距离井眼10 m处,利用FEPG软件模拟了孔隙压力随生产时间的变化关系,见图5。由图5可知,在垂直裂缝面方向距离井眼一定范围内,致密油藏孔隙压力随着时间增加而减小,但是减小幅度降低,到最后孔隙压力基本不变。

3.2 地层有效应力变化规律

致密油藏地层骨架承受的有效应力对于重复压裂时裂缝的重新定向具有重要作用。

由图4可知,在平行裂缝方向上地层骨架承受的有效应力分量呈现相似的变化规律,随着距离增大而减小,当距离大于缝长后,有效应力分量保持稳定。这是由于流体的产出造成孔隙压力降低,导致骨架所受的有效应力增大;并且越靠近裂缝,孔隙压力降低越大,有效应力的变化幅度越大。

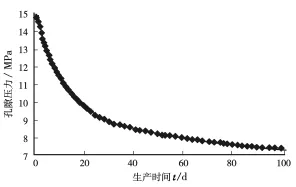
图5 垂直裂缝面距井壁10 m处孔隙压力随时间的变化关系

当生产时间一定时,平行裂缝方向上骨架承受的有效应力分量随距井壁的距离变化曲线,如图6所示。

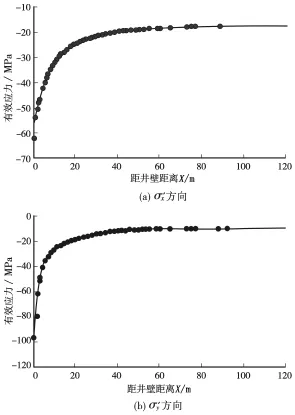
图6 平行裂缝方向有效应力分布(100 d)

当生产时间一定时,垂直裂缝方向上骨架所承受的有效应力分量随到井壁的距离变化曲线,如图7所示。

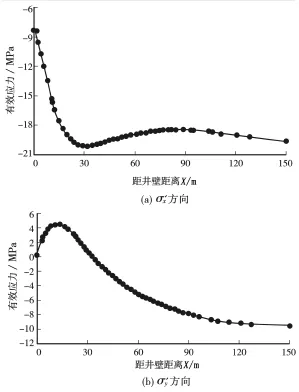
图7 垂直裂缝方向上有效应力分布(100 d)

由图7可知,在垂直裂缝面方向上致密油藏地层骨架承受的有效应力分量呈现先增大后减小的变化规律,甚至出现了拉压力变换区域,但是总体上有效应力呈增大趋势;通过对比平行和垂直方向地层有效应力可知,在距井眼相同位置处平行裂缝方向有效应力分量要远大于垂直裂缝方向。

选取垂直裂缝面方向上距离井眼10 m处,利用FEPG软件模拟了有效应力随生产时间变化关系,如图8所示。

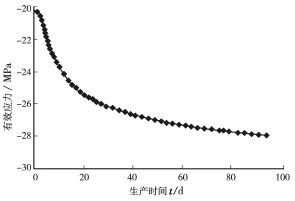
图8 垂直裂缝面距井壁10 m处有效应力随时间的变化关系

由图8可知,致密油藏储层有效应力随生产时间的增大而增大,最后趋于稳定,这是由于人工裂缝诱导应力的影响保持恒定,但是孔隙压力降低造成的。

4 结 论

(1)建立了致密油藏储层流固耦合模型和有限元力学模型,利用FEPG平台开发软件,模拟了重复压裂前人工裂缝和生产时间对致密储层原应力场分布的影响,为裂缝重新定向提供依据。

(2)致密油藏生产过程中,会在人工裂缝周围形成椭圆压降区,从边界到裂缝孔隙压力会依次递减,随着生产时间的增加,压降区不断增大,但最终趋于圆形。

(3)与平行裂缝方向相比,在垂直裂缝面方向上人工裂缝影响的压降范围要大一些,大约为裂缝半长的距离;裂缝对孔隙压力的影响随生产时间的增加而减小,最终孔隙压力趋于恒定。

(4)随着生产时间增加,储层流体减少,储层孔隙压力降低,有效应力增大;但是随着与裂缝距离的增大,有效应力呈现减小的趋势,并且在裂缝诱导应力的影响下,垂直裂缝方向上有效应力出现了拉压变换的现象。

[1] 胡文瑞.中国低渗透油气的现状和未来[J].中国工程科学, 2009,11(8):29-36.

[2] 陕亮,张万益,罗晓玲,等.页岩气储层压裂改造关键技术及发展趋势[J].地质科技情报,2013,32(3):156-161.

[3] 祝俊峰,蔡文新,姚飞,等.桩74断块南区重复压裂技术[J].石油学报,1998,19(3):73-76.

[4] SIEBRITS E,ELBEL J L,DETOUMAY E,et al.Parameters affecting azimuth and length of a secondary fracture during a refracture treatment[R].

[5] 董光,邓金根,朱海燕,等.重复压裂前的地应力场分析[J].断块油气田,2012,19(4):485-491.

[6] 余浩,曾永清,李薇,等.流-固耦合作用综述[J].西部探矿工程,2008(2):44-47.

[7] 程远方,沈海超,赵益忠,等.天然气水合物藏开采物性变化的流固耦合研究[J].石油学报,2010,31(4):607-611.

[8] 刘建军,冯夏庭.我国油藏渗流-温度-应力耦合的研究进展[J].岩土力学,2003,24:646-649.

[9] 孙峰,李行船,熊廷松,等.低渗透油藏水力压裂井应力场转向定量评价[J].断块油气田,2012,19(4):489-492.

[责任编辑]王艳丽

TE357

A

1673-5935(2016)04-0030-04

10.3969/j.issn.1673-5935.2016.04.009

2016-10-13

孙元伟(1988—),男,山东东营人,中国石油大学胜利学院油气工程学院助教,硕士,主要从事水力压裂研究。