混凝土SHPB试验的数值模拟

秦佳俊，夏 松，陈贵炫， 杨富莲

（1．广州大学 土木工程学院，广东 广州 510006；2．皖西学院 建筑与土木工程学院，安徽 六安 237012；3．广东工业大学 土木与交通工程学院 广东 广州 510006）

混凝土SHPB试验的数值模拟

秦佳俊1，2，夏 松2，陈贵炫3， 杨富莲2

（1．广州大学 土木工程学院，广东 广州 510006；2．皖西学院 建筑与土木工程学院，安徽 六安 237012；3．广东工业大学 土木与交通工程学院 广东 广州 510006）

利用有限元软件ANSYS/LS-DYNA，运用HJC本构模型，对混凝土试件的SHPB试验进行数值模拟，重构了混凝土在低、中、中高以及高应变率下的应力应变曲线，并且对试件的破坏形态进行了模拟。研究表明，HJC模型可以很好地模拟混凝土材料的力学性能，重构的应力应变曲线在曲线形态和峰值应力上均与SHPB试验拟合良好，数值模拟得到的混凝土的破坏形态也与SHPB试验一致，确定该强度混凝土材料HJC本构模型材料参数的方法具有通用性。

混凝土；应力应变曲线；SHPB试验；HJC本构模型

0 引 言

混凝土因为其较强的耐久性和较高的强度，广泛用于工业建筑、民用建筑、道路、桥梁以及防爆结构和军事设施中，这些建筑在承受静力荷载的同时，还要承受较大的动力荷载的作用，比如，工业建筑受到吊车荷载的作用、高层建筑受到地震荷载和风荷载的作用、路面受到汽车荷载的冲击作用等。混凝土结构受到动力荷载的作用时，会以高于静力荷载数十倍数量级的应变速率产生变形，并且表现出与静力荷载完全不同的力学性能，由于动力荷载的破坏性比静力荷载大很多，一些特殊的混凝土结构在设计时，动力荷载往往成为控制荷载，研究混凝土结构在冲击荷载等动力荷载作用下的力学性能及本构关系，对于动力荷载作用下混凝土的工程应用以及新型混凝土的开发具有实际的工程指导意义。

目前对于混凝土的动态本构模型采用最多的是HJC模型，HJC模型是T.J. Holmquist等[1]基于混凝土高应变率下的大变形问题提出的动态本构模型，它能够反映混凝土材料的脆性特点，同时考虑了材料损伤、应变率效应以及静水压力的影响。随着计算机的应用和发展，对混凝土本构模型的研究可以采用数值模拟的方法，既可以节约大量的试验经费，又可以完善试验的不足，同时试验结果可以作为对数值模拟结果的检验。研究人员在混凝土本构模型的数值模拟上获得了一些重要的结论，但是在模拟中也存在一些不足。孙远翔等[2]通过考虑入射应力幅值、试件应力幅值、透射波形等，证明可以通过数值模拟获得混凝土材料的本构参数；曹吉星等[3]对C80和C100的混凝土进行了SHPB试验的数值模拟，但是在数值模拟过程中，加载的入射波与SHPB试验入射波的波形有差异，虽然也得到了应力应变曲线，但是对于HJC模型的本构参数不具有通用性；巫绪涛等[4]用HJC模型模拟SHPB试验，解决了罚函数中罚因子合理数值的选取问题，证明了混凝土试件在数值模拟和SHPB试验中具有相似的力学行为，但其得到的应力应变曲线不够均匀。本文利用有限元软件ANSYS/LS-DYNA，充分考虑了数值模拟加载的入射波形与SHPB试验中入射波波形的一致性，以0.3 MPa气压控制下的入射波作为作用在试件上的加载波，通过两次对HJC模型的材料参数进行调整和多次试算，重构了控制气压分别0.2 MPa、0.3M Pa、0.4 MPa和0.5 MPa时试件的应力应变曲线，并且模拟了混凝土试件的破坏形态。在SHPB试验中，主要通过调整加载装置释放的气压值来调整子弹的冲击速度，不同的控制气压对应不同的应力脉冲作用，不同的应力脉冲的作用下，混凝土试件的应变率不同，在模拟中0.2 MPa、0.3 MPa、0.4 MPa和0.5 MPa的控制气压分别对应低、中、中高和高应变率。

1 混凝土试件的有限元模型

为了使模拟能最大限度地反映真实情况，并且考虑非一维效应的影响，本模型采用三维建模，模型中的入射杆、混凝土试件、透射杆等都采用ANSYS/LS-DYNA中的SOLID64三维实体单元，SOLID64三维实体单元有8个结点，每个结点3个自由度，即沿X、Y、Z的平动自由度，可用于各向异性实体结构的3D建模，而且有应力刚化和大变形能力，能较好地模拟混凝土试件、子弹、以及入射杆和透射杆的力学性能。入射杆、透射杆采用了钢材的弹性模型，其主要的材料参数为ρ =2800 kg/m³、E=2100GPa、γ=0.3。在有限元模型中，各个部分的尺寸跟SHPB试验的尺寸一致，为了节约计算时间，本数值模拟采用1/4建模，采用对称约束，有限元模型和网格划分如图1所示。

图1 混凝土试件的有限元模型

在本模拟过程中采用单点积分算法，计算过程中为了避免因单元刚度矩阵的秩不足导致的沙漏效应，可以在端面间直接撞击的接触问题采用对称罚函数[4]，接触刚度罚函数因子k=2。

2 数值模拟与SHPB试验应力应变曲线的拟合

2.1 混凝土试件加载及HJC模型原始参数的模拟结果

常规的SHPB试验的加载波是矩形波，为了使冲击波下应力应变曲线具有均匀性，对本次数值模拟的加载波采用脉冲整形技术进行处理，通过物理滤波手段使入射脉冲陡峭的上升段变成坡度减小的斜坡波形。SHPB试验中子弹撞击入射杆的速度是通过测速装置测出的，数值模拟中入射波的加载是直接对子弹施加，在本次数值模拟中，以0.3 MPa气压控制下的入射波作为加载波，进行混凝土在冲击荷载下应力应变曲线的重构，在进行数值模拟时，采用*MAT_ADD_EROSION侵蚀失效准则来控制单元的失效。本构模型的材料参数全部为HJC模型的原始材料参数时，混凝土试件在0.3 MPa控制气压作用下，即中应变率下重构的应力应变曲线如下图2（a）所示，在图2（a）中可以看出，数值模拟得到的混凝土试件的应力应变曲线光滑，不像SHPB试验那样存在激荡现象，这是因为在数值模拟过程中假设混凝土是均质材料；数值模拟重构的应力应变曲线和SHPB试验得到的应力应变曲线在弹性阶段、塑性阶段以及卸载阶段均不一致，这说明采用原始材料参数的HJC模型不能正确描述本试件的力学性能，可以考虑对HJC模型的材料参数进行修正。

2.2 HJC模型参数调整与分析

Holmquist等[1]给出的HJC动态本构模型的参数共21个，分别是静载抗压强度fc’=48 KPa；密度ρ0=2440 kg/m³；6个强度参数A、B、C、N、Smax、G；3个损伤参数D1、D2、 εfmin；8个压力参数Pc、 µc、k1、k2、k3、P1、 µ1、T；应变率 ε0和失效类型fs。对于不同强度等级的混凝土， 21个HJC本构模型材料参数里可以通过简单的试验和计算调整一部分[5]，比如，最简单的一个参数密度ρ0可以通过测量混凝土试件的质量计算得到，通过混凝土的静载抗压强度试验可以确定试件的fc’，通过静载抗压强度试验获得的应力应变曲线可以计算该强度混凝土的弹性模量E，普通混凝土受压时，混凝土的泊松比为一常量，进而可以计算出剪切模量G、混凝土压碎时的体积应力Pc =fc’/3、压碎的体积应变 µc，混凝土的极限体积应力P1以及体积应变 µ1也可以通过计算得到。至此，根据试验和计算可以获得的参数有：ρ0、G、Pc、µc、µ1、P1。其他参数采用原始参数，断裂应变 εfmin值为该强度混凝土试件静载试验中试件破坏时的极限应变值，失效类型fs的取值与εfmin相同。调整了部分材料参数后重构混凝土的应力应变关系与SHPB试验应力应变曲线的比较如下图2（b）所示。

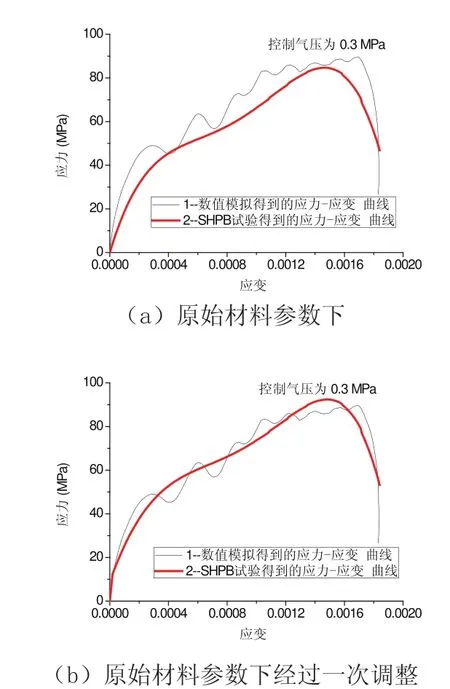
图2 中应变率时下的应力应变曲线

从图2（b）中可以看出，数值模拟得到的应力应变曲线在线弹性阶段和塑形阶段前期与SHPB试验得到的应力应变曲线基本吻合，这说明在此阶段混凝土试件处于一维应力状态。在塑形阶段后期和试件破坏阶段，数值模拟的应力应变曲线与SHPB试验得到的应力应变曲线的拟合情况不好，原因在于随着应变的增大，横向泊松比效应使得非一维应力状态加剧并且混凝土试件和加载装置存在一些尺寸缺陷；除了应力应变曲线的拟合存在差异，数值模拟得到的峰值应力较SHPB试验的峰值应力高，为了提高数值模拟结果和试验的拟合精度，以及深入研究冲击荷载等动力荷载作用下混凝土的的力学性能、本构模型以便于混凝土的工程应用，HJC的材料参数还需要进一步的调整。

HJC动态本构模型的材料参数影响混凝土试件的应力应变关系曲线及峰值应力，参考文献[6-7]表明，参数A和B影响试件的峰值应力；参数-的影响试件应变率效应的结果；参数N的取值影响屈服上升段斜率以及脉宽。本次模拟在满足个参数物理意义的情况下，通过不断调整A、B、C、N的取值和重复试算来增加数值模拟应力应变曲线与SHPB试验的拟合精度。经过两次参数调整后，混凝土HJC本构模型的材料参数见下表1。

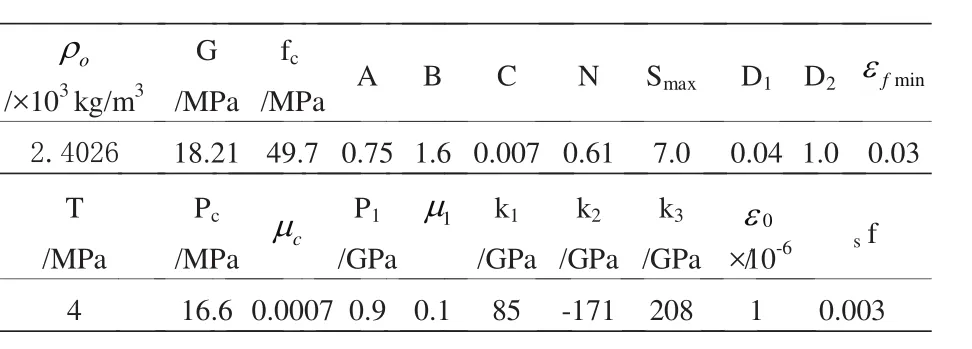
表1 混凝土HJC本构模型的两次调整后的材料参数

2.3 混凝土试件经两次材料参数调整后的数值模拟结果及分析

经过两次调整混凝土HJC本构模型的材料参数，混凝土试件在控制气压为0.3 MPa时数值模拟的应力应变曲线与SHPB试验应力应变曲线的对比见图3（b），从图上可以看出，数值模拟的应力应变曲线的形状跟SHPB试验的曲线形状相似，无论是在弹性阶段、塑形阶段还是试件的破坏阶段均拟合较好，并且数值模拟得到的峰值应力为89.5 MPa，与SHPB试验得到的峰值应力90.6 MPa[8]相差不多。继续采用这套参数进行控制气压分别为0.2 MPa、0.4MPa、0.5MPa下应力应变曲线进行重构，得到的数值模拟应力应变曲线与SHPB试验应力应变曲线的比较如图3（a）、3（c）、3（d）所示，可以看到利用这套材料参数重构的应力应变曲线与试验得到的应力应变曲线有较高的拟合精度，且峰值应力相近，表明该HJC本构模型的材料参数的确定方法对本强度的混凝土具有通用性。

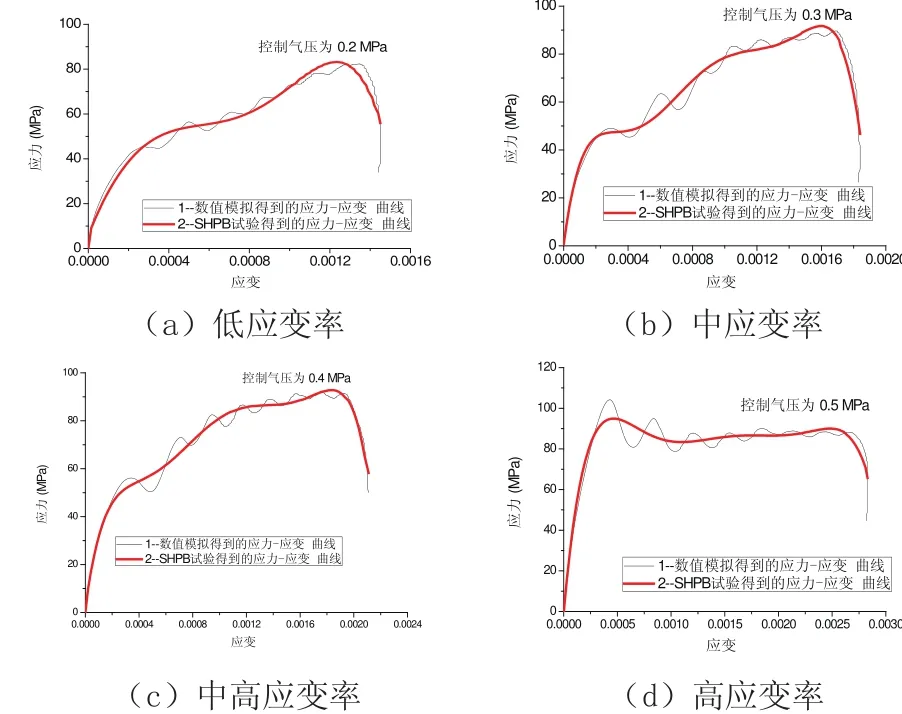
图3 材料参数两次调整后不同应变率下应力应变曲线的比较

3 数值模拟的破坏形态与SHPB试验的比较

混凝土试件在不同应变率下的破坏形态不同，在冲击压缩试验中，随着冲击速度的增加应变率逐渐增大，混凝土试件的破坏程度也随之不断加大[8]。和混凝土试件的静载破坏状态不同，混凝土试件在受到冲击荷载作用时，其破坏点有多点，多点同时开裂扩展至破坏。混凝土试件在静载作用下，由于混凝土结构的非均匀性，试件内部就有大量的微裂缝和微孔洞，断裂力学原理表明，一条或数条较大的裂缝 (或微孔洞处) 会优先发展成主裂缝，随着时间的推移，主裂缝最终形成贯穿裂纹；在冲击荷载作用下，主裂纹来不及贯通，试件表面的微裂纹增多，多点微裂纹同时起裂，随着应变率的增加，试件破坏形成的碎块尺寸越小，起裂的微裂纹越多且尺寸越小，试件吸收的能量也越多。图4依次为混凝土试件在低、中、中高、高应变率下SHPB试验的破坏形态。

图4 不同应变率下SHPB试验混凝土试件破坏形态比较

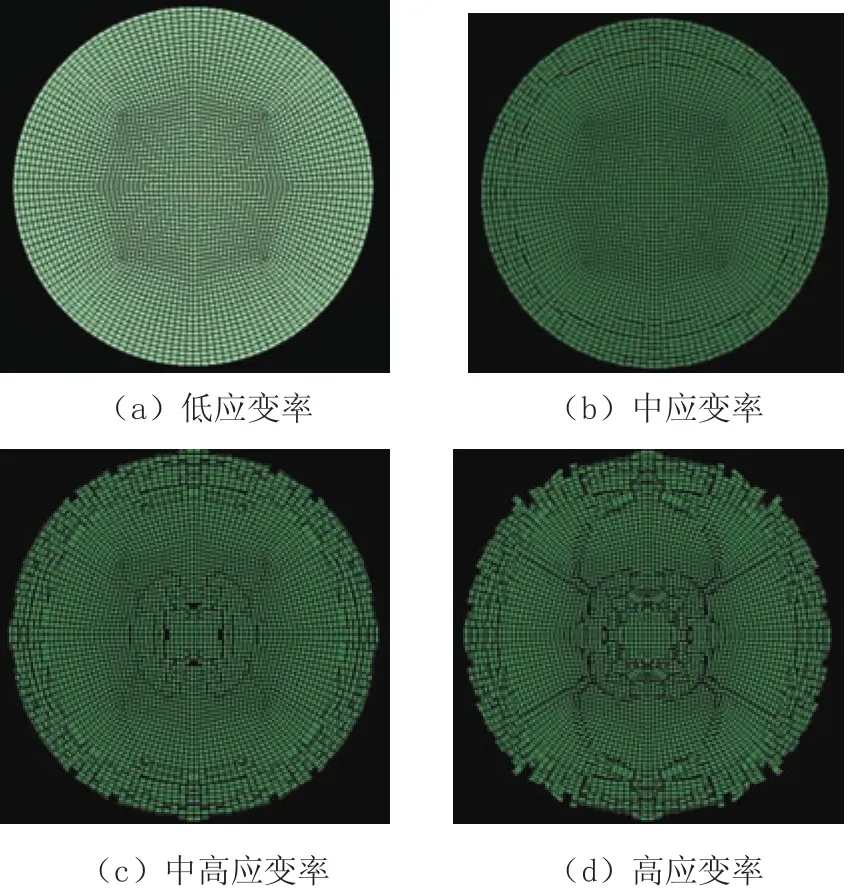
图5 不同应变率下数值模拟混凝土试件破坏形态比较

图5依次为混凝土试件在低、中、中高、高应变率下数值模拟的破坏形态。对比图4、图5，在低应变率下，如图4（a）和图5（a）所示，数值模拟的破坏形态表现为没有出现单元的删减，试件基本没有破损；在中应变率下，如图4（b）和图5（b）所示数值模拟的破坏形态表现为沿着试件的周围出现单元的删减，试件表面出现破损，；在中高应变率下，如图4（c）和图5（c）所示，在数值模拟破坏形态表现为在试件四周及内部均出现了单元的删减，试件表面出现贯穿的裂缝；在高应变率下，如图4（d）和图5（d）所示，数值模拟破坏形态中可以看到大量单元的删减试件粉碎，破坏严重，只有核心区混凝土尚完整，可知混凝土试件SHPB试验和数值模拟的破坏形态一致。

4 结语

[1]T.J.Holmquist,G.R.Johnson,W.H.Cook.A computational constitutive model for concrete subjective to large strains,high strain rates,and high pressures[A].//Proceedings of 14th International Symposium on Ballistics[C]. Quebec City,Canada,1993:591-600.

[2]孙远翔,赵迁,宁建国. 混凝土材料SHPB实验的数值模拟［A］.//计算爆炸力学进展［C］.山东青岛：2006. 319-326.

[3]曹吉星,陈虬,张吉萍.混凝土S H P 试B验的数值模拟及应力均匀性[J].西南交通大学学报,2008, 43(1):67-70.

[4]巫绪涛,孙善飞,李和平.用HJC本构模型模拟混凝土SHPB实验[J].爆炸与冲击, 2009, 29(2)：137-142.

[5]张凤国,李恩征.混凝土撞击损伤模型参数的确定方法[J].弹道学报, 2001,13(4):12-16+23.

[6]孙善飞.混凝土SHPB实验的数值模拟[D].合肥:合肥工业大学,2007.

[7]李耀.混凝土HJC动态本构模型的研究 [D].合肥:合肥工业大学,2009.

[8]陈贵炫. 橡胶混凝土的抗冲击性能研究[D].广州:广东工业大学,2011.

通过对混凝土试件SHPB试验的数值模拟，得到了如下结论：

（1）HJC模型下混凝土试件受冲击荷载的应力-应变曲线和破坏形态与SHPB试验中混凝土表现出的较一致，说明HJC模型可以很好地模拟混凝土材料的动力性能;

（2）数值模拟过程中混凝土试件在低、中、中高以及高应变率下的应力应变曲线与SHPB试验的应力应变曲线在曲线形态、峰值应力上均拟合良好，表明HJC模型参数的确定方法对于不同应变率下的混凝土具有通用性。混凝土试件在中应变率下的应力应变曲线的曲线形态与SHPB试验的应力应变曲线在下降段略有差异，除了网格划分要精细外还可以从失效方式方面进行入手进行研究。

（3）数值模拟过程中采用主应变侵蚀失效准则*MAT_ADD_EROSION来控制单元的失效，混凝土试件在低、中、中高以及高应变率下得到的破坏形态与SHPB试验的破坏形态一致。

Numerical Simulation of SHPB Experiment for Concrete

QIN Jiajun1,2，XIA Song2，CHEN Guixuan3， YANG Fulian2

(1. Civil Engineering School,Guangzhou University, Guangzhou ,510006,China; 2.Architecture and Civil Engineering School,West Anhui University,Lu’an ,237012, China; 3.Civil and Transportion Engineering School, Guangdong University of Technology,Guangzhou,510006, China;)

By using finite element software ANSYS/ls-dyna,the SHPB test for concrete has been numerically simulated by using the HJC model,the stress strain curve of concrete at different strain rates are reconstructed,and the failure patterns of the specimens were simulated.The research shows that the HJC model can well simulate the mechanical properties of concrete,the stress strain curves are in agreement with the SHPB test on the curve shape and the peak stress,and the failure pattern of concrete obtained from the numerical simulation is also consistent with the SHPB test. The method for determining material parameters of HJC constitutive model of concrete material is universal.

concrete;stress-strain curve;SHPB test;HJC model

TU502.6

A

2095-8382(2016)06-048-05

10.11921/j.issn.2095-8382.20160611

2016-07-04

安徽省高校自然科学基金（KJ2016A748）；六安市定向委托皖西学院市级研究项目（2014LWA005）；皖西学院校级自然科学研究项目重点项目（KJ103762015B12）

秦佳俊（1986—）女，博士研究生，主要研究方向为材料及结构的动力特性、动力响应分析。