敞开式桁架组合简支梁桥结构车辆荷载下振动响应分析

曹 皓, 马乙一,陈安英,完海鹰

（1.安徽省交通控股集团有限公司，合肥，230011；2.合肥工业大学，合肥 230009）

敞开式桁架组合简支梁桥结构车辆荷载下振动响应分析

曹 皓1, 马乙一1,陈安英2,完海鹰2

（1.安徽省交通控股集团有限公司，合肥，230011；2.合肥工业大学，合肥 230009）

以某敞开式桁架组合简支梁桥结构为工程背景，基于车桥耦合振动分析理论，采用一种简化的车桥耦合振动分析方法，对该公路桥进行车辆荷载作用下的振动响应分析。分析研究了四种行车方式、六种行驶车速下组合桁架梁桥的振动响应。分析结果表明，该桥梁的各项动力指标满足设计安全要求。分析方法可为类似敞开式桁架组合简支梁桥结构设计提供参考。

敞开式、组合梁桥、振动、响应

0 引 言

敞开式钢管-混凝土桁架组合梁桥结构主要包含主桁架、桥面系结构两部分。主桁架由上弦杆、腹杆及下弦杆组成。通常上弦杆、端斜杆可采用钢管混凝土系杆，腹杆为钢管构件，下弦杆采用预应力混凝土梁；主桥桥面系结构由桥面板、中横梁及端横梁组成，与主桁架下弦杆共同参与结构受力；横梁可采用预应力混凝土梁。敞开式钢管-混凝土桁架组合梁桥具有自重轻、跨越能力强、建筑高度低、造型简洁美观、造价相对较省等诸多优势，是一种具有创新意义的新型梁式桥梁。

基于车桥耦合振动理论，分析桥梁结构在车辆荷载作用下的振动响应，是研究桥梁动力性能的重要手段。以某敞开式钢管-混凝土桁架组合梁桥为工程背景，在设计分析阶段，利用通用有限元软件MIDAS/CIVIL，采用一种简化的车桥耦合振动分析方法对该公路桥进行车桥耦合振动分析[1-3]。通过有限元分析结果，判断该桥梁结构的动力特性。

1 车桥耦合振动分析理论

1.1 桥梁模型的建立

处理车桥耦合振动问题时，模态坐标法和有限元法是建立桥梁模型的有效方法[4-5]。模态坐标法用于车桥耦合问题求解的时间较早，可简便有效地减少结构自由度，实现简单桥梁结构车桥运动微分方程的解耦，得到解析解。但该方法只能体现结构的整体振动特性，无法考虑结构细部；若考虑复杂桥梁结构的多阶振型参与贡献，计算自由度大量增加，缺点较为突出。目前广泛采用的建立桥梁结构分析模型的方法是杆系有限元法。采用杆系有限元法建立桥梁模型时，为减少桥梁结构的自由度，需采用“静力凝聚法”；对于斜拉桥、悬索桥等复杂的桥梁，需对结构做简化处理，这会降低结构细部计算结果的准确性，通常在建模时采用板壳单元、实体单元等混合建模，共同模拟桥梁结构。对于桁架式简支桥梁，杆系有限元法计算精度较高[6]。

1.2 车桥耦合振动简化设计

论文研究的对象为高速公路桥梁结构，常用的车桥耦合振动分析方法将车辆与桥梁结构耦合成一个联结模型进行分析，计算效率较低，计算分析过程较繁琐、复杂。在桥梁结构设计阶段，若只重点关注桥梁结构的振动响应，可采用车桥耦合振动简化设计方法，不考虑由于车行道路的不平顺对车辆行驶舒适度的影响，设计误差可满足工程设计要求[7-8]。

采用基于MIDAS/CIVIL的振型叠加时程分析法进行车桥耦合振动模型求解。简化分析模型将作用在桥梁结构节点上的车辆动荷载简化成一种瞬间作用后即将消失的冲击荷载，不考虑移动车辆的惯性力与阻尼力，将其轮胎对桥梁的作用简化为匀速移动的力P(t)[9]，P(t)为随时间变化的三角形荷载，如图1所示，t1为车辆从桥梁某一横向联系梁中点行驶至相邻横向联系梁中点的时间，t2=2t1。

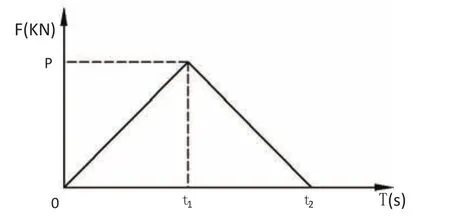
图1 车辆三角形荷载

根据《公路桥涵设计通用规范》（JTG D60-2004）4.3.1条，车辆在桥梁上行驶时，车辆荷载分布方式如图2所示[10]。单辆车对应五个移动荷载，可简化成三个三角形时程荷载函数。时程荷载函数1、2、3分别对应车辆前轴、中轴、后轴重力标准值，即图1中P值分别为30 KN、120 KN、140 KN。五个移动荷载在桥梁上保持图2所示间距匀速行进。

图2 车辆荷载分布示意图

基于MIDAS/CIVIL的简易车桥耦合振动分析步骤如下：

（1）建立结构模型，输入质量数据；

（2）输入特征值分析数据，进行特征值分析；

（3）查看特征值分析结果，研究桥梁自由振动特性；

（4）输入时程分析数据，进行时程分析；

（5）查看时程分析结果，研究桥梁在车辆荷载下的动力特性；

（6）桥梁结构车致振动设计评价。

2 工程概况

某单跨60 m敞开式钢管-混凝土桁架组合简支梁桥为高速公路跨线桥。桥梁下部结构为柱式桥墩、桩基础，上部结构由两片敞开式主桁架及桥面体系组成。其上弦杆、端斜杆为钢管混凝土结构，腹杆为钢管结构，下弦杆为预应力混凝土结构。上部结构与柱式桥墩采用抗震铅芯支座连接[11]。主桁架采用不带竖杆的华伦式三角形腹杆体系，节间长度4 m，主桁架高度6.8 m，高跨比为1/8.82。两片主桁架中心距为13.65 m，宽跨比为1/4.40，桥面行车道宽度12.125 m。桥梁上部结构布置如图3所示。

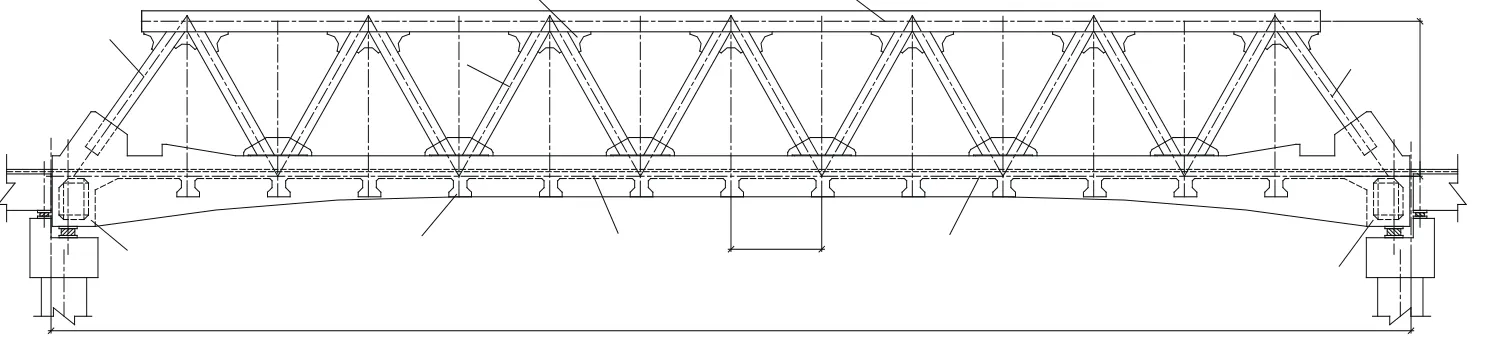
图3 单跨60 m桁架组合梁桥桥型布置图（mm）

图4 桥梁结构有限元模型

3 有限元模型

利用MIDAS/CIVIL建立桥梁结构有限元模型，如图4所示。

利用建立的有限元模型对桥梁进行特征值分析和车桥耦合振动时程分析。车桥耦合振动过程中，桥梁跨中位置反应最为明显，可反映桥梁的动力特性。定义车辆的行驶方向在图4中为自左向右行驶。从桥梁跨中选取三个代表性节点作为研究对象，三节点依次位于外车道纵梁跨中、内车道纵梁跨中、桥梁跨中横向联系梁中点，分别记为节点1、节点2、节点3。

4 桥梁自由振动特性

对桥梁进行特征值分析，得到结构基本自振周期为0.935 s，第100阶模态周期为0.015 s。结构第一阶自由振动模态为全桥横桥向振动，前六阶自振振型特征如图5，自振频率值见表1。

表1 结构前六阶模态自振频率及振型特征

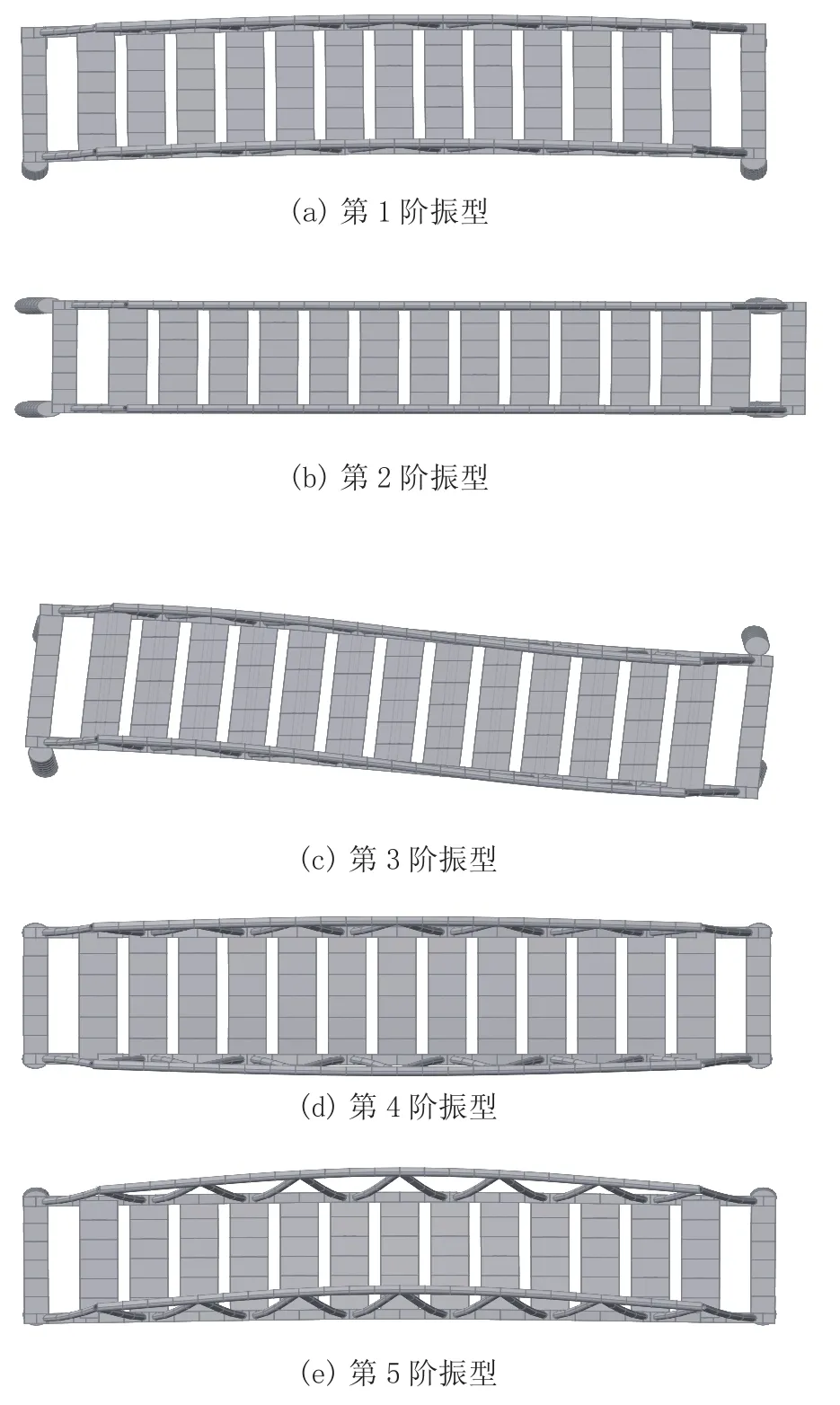
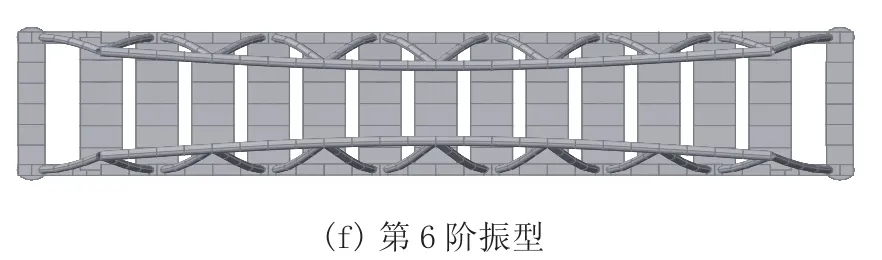
图5 桥梁前六阶振型模态

5 桥梁在车辆荷载作用下的动力特性

研究四种行车方式，行车方式一：单辆车从桥梁中间车道匀速通过；行车方式二：单辆车从桥梁内车道匀速通过；行车方式三：一辆车从中间车道，另一辆车从内车道同时匀速通过；行车方式四：三辆车分别从中间车道、内车道、外车道同时匀速通过。研究1 km/h、60 km/h、80 km/h、100 km/h、120 km/h、140 km/h等六种行驶车速。只考虑桥梁的竖向反应[12]。

5.1 桥梁动力特性评价标准

公路桥梁相关规范没有对车桥耦合振动作用下桥梁的动力特性给出详细的评价标准。参考《铁路桥涵设计基本规范》（TB 10002.1-2005）中的规定[13]，简支钢筋混凝土和预应力混凝土桥梁桥跨结构，由列车静活载（不计冲击力）所引起的竖向挠度不应大于L/800，其中L为简支梁或连续梁验算跨的跨度。论文研究桥梁跨度为60 m，竖向挠度容许值为75 mm。欧洲规范EUROCODE规定，计算桥梁振动加速度时至少考虑结构的三阶振型，频率考虑至flim=max[30，λf0]（Hz），f0为桥梁结构一阶自振频率，λ=1~2。明桥面桥梁桥面板的竖向加速度限值为0.5 g。冲击系数是评价桥梁动力特性的重要指标，根据《公路桥涵设计通用规范》（JTG D60-2004），研究的桥梁结构基频为1.069 Hz，其冲击系数μ取0.05[10]。冲击系数也可表示为桥梁结构指定位置最大动位移与最大静位移之比，即1+μ=△d/△s。模型计算结果可与设计规范计算结果进行对比，为桥梁设计提供参考。

5.2 设计车速下桥梁动力特性

桥梁设计时速为120 km/h，相邻横向联系梁中心间距为4 m。图1中t1值为0.12 s，t2值为0.24 s。时程分析时间步长取0.001 s。三角形时程荷载函数同1.3节。桥梁跨度为60 m，车辆前轮与后轮间距为15 m，故研究车辆前轮行驶80 m过程中桥梁的动力反应。单辆车从中间车道匀速通过时，桥梁1、2、3节点的竖向位移、加速度曲线如图6~9所示。节点1、2的最大竖向位移为-2.199 mm、最大竖向加速度为-74.109×10-³ m/s²。节点3的最大竖向位移为-3.287 mm、最大竖向加速度为-617.628×10-³ m/s²。

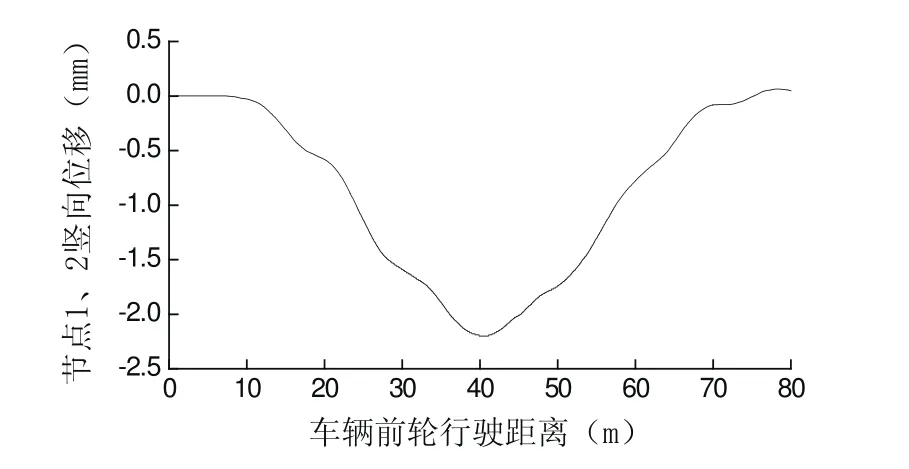
图6 节点1、2竖向位移曲线图

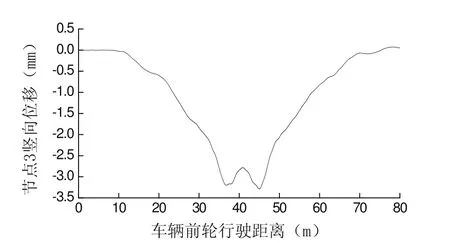
图7 节点3竖向位移曲线图

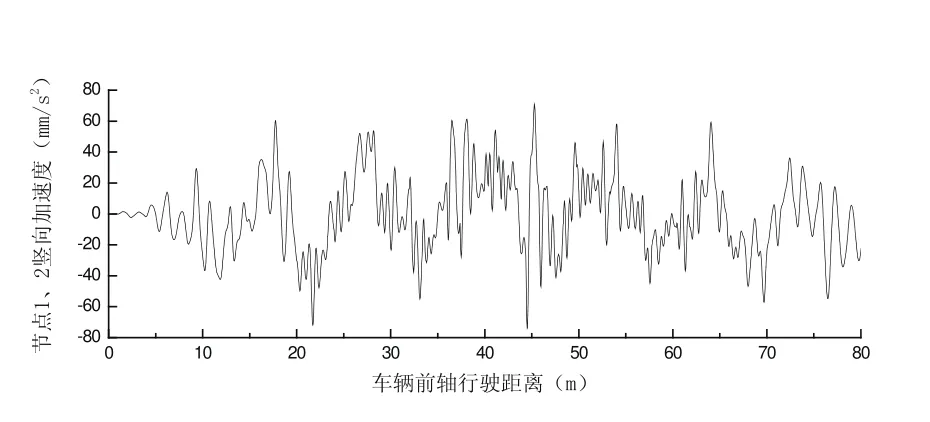
图8 节点1、2竖向加速度曲线图

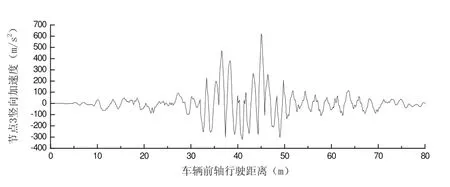
图9 节点3竖向加速度曲线图

5.3 桥梁动力特性对比分析

对四种行车方式，六种行驶车速下，桥梁结的动力反应进行对比分析。竖向位移、加速度值取绝对值。桥梁在1 km/h行驶车速下的动力特性，可以近似代替桥梁在车辆移动荷载作用下的静力反应。

5.3.1 行车方式一单辆车从中间车道匀速通过时，根据对称性，节点1、节点2具有相同的动力特性。随着车速的不断增大，各节点位置竖向位移无明显变化，且值较小，节点1、2的竖向位移最大值为2.199 mm，节点3为3.425 mm；各节点的竖向加速度增加明显，节点1、2的竖向加速度在140 km/h车速下达最大值104.965×10-³ m/s²，节点3的竖向加速度在100 km/h车速下达最大值833.620×10-³ m/s²。节点1、2最大冲击系数为0.002，节点3最大冲击系数为0.022。

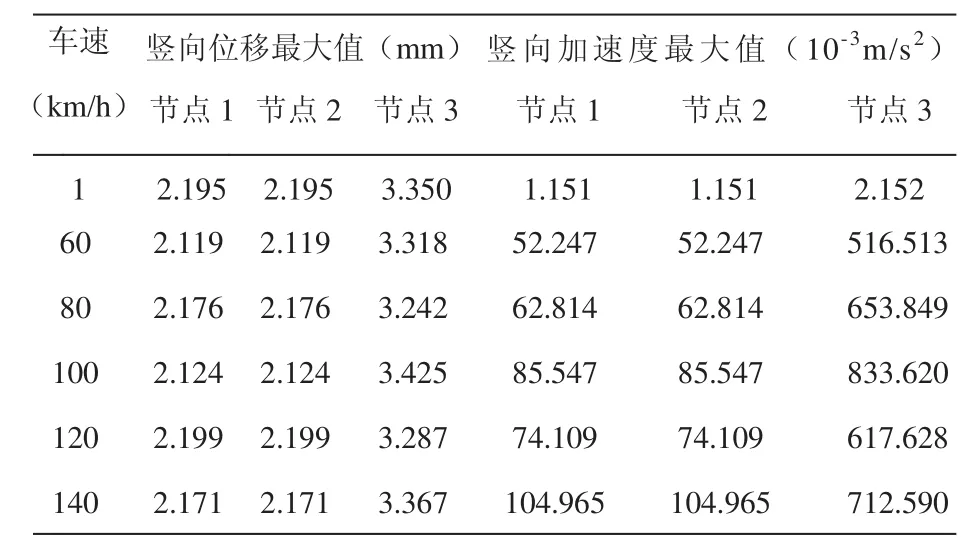
表2 行车方式一节点动力响应

5.3.2 行车方式二

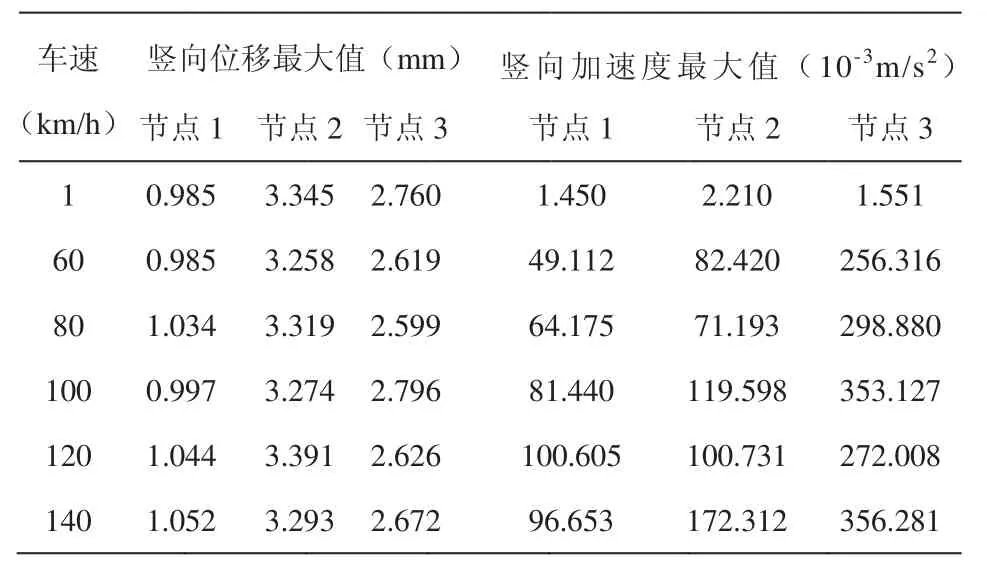
表3 行车方式二节点动力响应

单辆车从内车道匀速通过时，各节点动力特性表现出明显差异。随着车速的不断增大，各节点位置竖向位移无明显变化，且值较小，节点2的竖向位移值相对较大，其最大值为3.391 mm；节点1、2、3的竖向加速度最大值出现在不同的车速下，最大值分别为100.605×10-³ m/s²、172.312×10-³ m/s²、356.281×10-³ m/s²。节点1、2、3最大冲击系数分别为0.068、0.014、0.013。

5.3.3 行车方式三

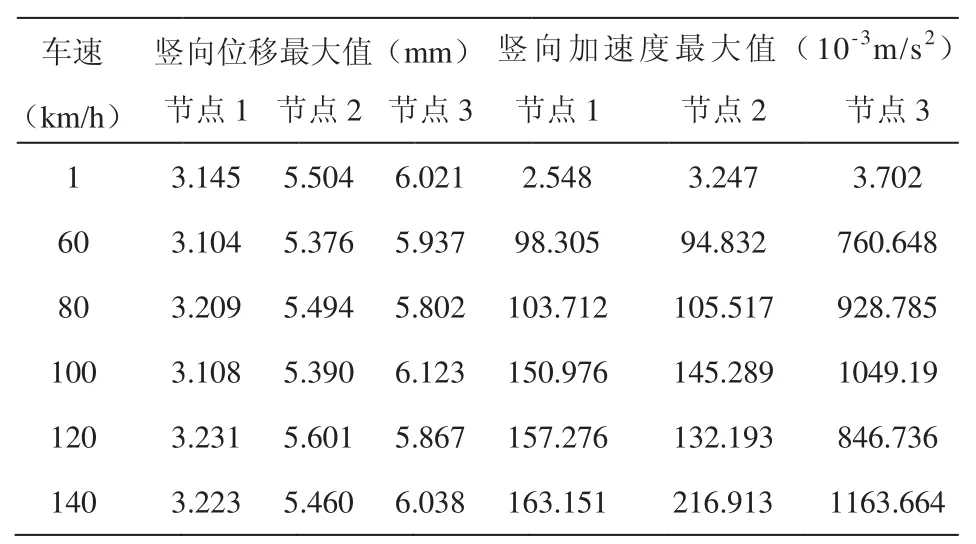
表4 行车方式三节点动力响应

一辆车从中间车道，另一辆车从内车道同时匀速通过时，各节点动力特性表现出明显差异。随着车速的不断增大，各节点位置竖向位移无明显变化，且值较小，节点1、2、3的最大值分别为3.231 mm、5.601 mm、6.123 mm；节点1、2、3的竖向加速度最大值皆出现在140 km/h的车速下，分别为163.151×10-³ m/s²、216.913×10-³ m/s²、1163.664×10-³ m/s²。节点1、2、3最大冲击系数分别为0.027、0.018、0.017。

5.3.4 行车方式四

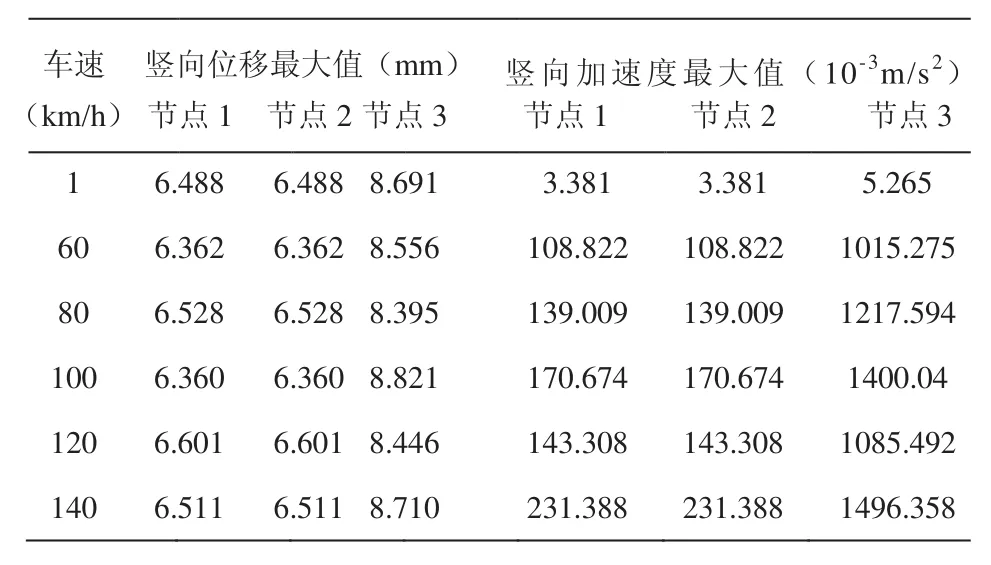
表5 行车方式四节点动力响应

三辆车分别从中间车道、内车道、外车道同时匀速通过时，桥梁所受车辆荷载值最大。节点1、2、3的竖向位移受车速变化影响不明显，最大值分别为6.601 mm、6.601 mm、8.821 mm。

节点1、2、3的竖向加速度最大值皆出现在140 km/h的车速下，分别为231.388×10-³ m/s²、231.388×10-³ m/s²、1496.358×10-³ m/ s²。节点1、2最大冲击系数为0.017，节点3最大冲击系数为0.002。

6 结论

（1）桥梁在1 km/h行驶车速下的动力响应，可以近似反映桥梁在移动荷载作用下的静力反应。120 km/h为该桥梁的设计车速，该车速下各节点的竖向位移曲线变化明显，且幅度较大，加速度值明显高于1 km/h行驶车速的情况。

（2）四种不同的行车方式下，桥梁表现出不同的动力特性，单辆车从中间车道匀速通过、三辆车从三车道同时匀速通过时，由于对称性，节点1、2动力响应相同；另外两种行车方式下，桥梁具有一定的扭转效应，三节点动力响应差异较大。

（3）对比六种车速下桥梁的动力响应发现，车速对于桥梁竖向位移值影响并不明显，对加速度的影响较大。以三辆车分别从中间车道、内车道、外车道同时匀速通过时为例，六种行驶车速下，节点1、2的最大竖向位移在6.260 mm~6.601 mm范围内，节点3的最大竖向位移在8.446 mm~8.821 mm范围内，变化较小；当行驶车速为1 km/h时，节点1、2、3的最大竖向加速度都小于5.5×10-³ m/s²，当行驶车速为140 km/h时，节点1、2、3的最大竖向加速度分别为 231.388×10-³ m/s²、231.388×10-³ m/s²、1496.358×10-³ m/s²，变化幅度较大。

（4）研究的桥梁的竖向挠度容许值为75 mm，节点1、2的最大竖向位移为6.601 mm，节点3为8.821 mm，满足要求。明桥面桥梁桥面板的竖向加速度限值为0.50 g。节点1、2的加速度最大值为231.388×10-³ m/s²，节点3为1496.358×10-³ m/s²，满足要求。

（5）单辆车以140 km/h的行驶速度从桥梁内车道匀速通过时，以节点1计算的冲击系数最大，为0.068，与设计规范计算结果0.05相近。

（6）分析结果表明，在桥梁设计阶段，利用车桥耦合振动简化设计方法可以对桁架组合梁桥的车桥耦合振动响应进行分析。敞开式桁架组合简支梁桥在设计车辆动荷载作用下，具有较好的动力性能。

[1]杨建荣，李建中，申俊昕. 钢管混凝土系杆拱桥车桥耦合振动分析[J]. 北京工业大学学报，2012，38(6):847–853.

[2]严志刚，陈彦江，盛洪飞. 钢管混凝土拱桥在车辆荷载作用下的非线性动力响应分析[J]. 中国公路学报，2003，16(1):58–67.

[3]崔圣爱，祝 兵. 客运专线大跨连续梁桥车桥耦合振动仿真分析[J]. 西南交通大学学报，2009，44 (1)：66–71.

[4]李东旭. 高等结构动力学[M]. 北京： 科学出版社，2010.

[5]王勖成. 有限单元法[M]. 北京：清华大学出版社，2003.

[6]谢秉敏，向中富，王小松，等. 基于 ANSYS 的车桥耦合动力分析[J]. 重庆交通大学学报(自然科学版)，2012，31(5):935–938.

[7]桂水荣, 陈水生,潘登.多片梁组成的简支梁桥车桥耦合振动响应研究[J].中外公路，2008，28(4)：173–177.

[8]欧阳光，谈傅生.大跨度斜拉桥车桥耦合振动分析[J]. 中外公路，2013，33 (4):182–187.

[9]夏 禾，张宏杰，曹艳梅，等. 车桥耦合系统在随机激励下的动力分析及其应用[J].工程力学学报，2003，20 (3):142–149.

[10]中交公路规划设计院.公路桥涵设计通用规范：JTG D60-204[S].北京:人民交通出版社,2004.

[11]陈水生，马涌泉.铅芯橡胶支座隔震公路桥梁车桥耦合的振动响应[J].北京交通大学学报，2013，37(4):78–88.

[12]陈水生，李孟廷，桂水荣，等.多车激励公路简支梁车桥耦合振动响应分析[J]. 武汉理工大学学报，2014，36(3):101–106.

[13]铁道第三勘察设计院.铁路桥涵基本设计规范：TB 10002.1-2005[S].北京:中国铁道出版社，2005.

The vibration response analysis of open type truss compositesimply supported beam bridge under vehicle load

CAO Hao1, MA Yiyi1, CHEN Anying2, WAN Haiying2

(1. Anhui Transportation Holding Group CO.,LTD, Hefei, 230031, China;2.Hefei University of Technology, Hefei, 230009, China)

Taking one open type truss composite simply supported beam bridge as the engineering background, the vibration response analysis under vehicle load has been done by using a simplified analysis method based on theory of vehicle-bridge coupling vibration analysis. The vibration response of the composite truss beam bridge has been studied under four driving modes and six types of driving speed. The analysis result shows the dynamic parameters of bridge can meet the designing safety requirements. The analysis method can provide reference for the design of similar open type truss composite simply supported beam bridge.

open type, composite beam bridge, vibration, response

U448.22

A

2095-8382(2016)06-008-06

10.11921/j.issn.2095-8382.20160602

2016-04-19

曹皓（1984-），女，工程师，主要研究方向为桥梁结构分析。