大口径光学元件斜入射反射波前误差测量和计算

2016-02-11徐隆波朱日宏刘世杰郑万国

光学精密工程 2016年12期

徐隆波，周游，朱日宏，刘世杰*，郑万国

(1.南京理工大学电子工程与光电技术学院，江苏南京 210094;2.中国科学院强激光材料重点实验室，上海 201800;3.中国工程物理研究院，四川绵阳 621999;4.中国工程物理研究院激光聚变研究中心，四川绵阳 621999)

徐隆波1，3，周游2，朱日宏1，刘世杰2*，郑万国4

针对测量高功率激光驱动装置中大口径矩形反射光学元件的波前误差时测量角度和使用角度不完全相同引入的测量误差，提出了将测量角度下的反射波前转换到使用角度的反射波前的换算及恢复方法。首先分析了将斜入射测量角度下的波前转换到使用角度下波前的余弦换算方法，得到了实际测量角度与实际使用角度下的波前误差计算关系；然后计算并分析了双三次插值算法本身引起的中频PSD1(功率谱密度)误差，指出在满足有效口径测量的情况下，选择的入射角度应该与实际使用的角度尽可能的相接近。最后，基于410 mm×410 mm的熔石英反射镜开展了误差分析和实验验证。利用该方法将0°反射波前换算到45°反射波前，并将得到的测试结果与45°直接测量得到的测试结果进行了比较。结果显示上述结果的PV值相差0.01λ，RMS值相差0.003λ，PSD1值相差0.08 nm；表明该换算方法不仅能够准确计算出使用角度下反射波前的低频误差，而且能获得相对准确的中频段PSD1误差。

高功率激光装置；大口径光学元件；反射波前；波前误差；双三次插值；中低频误差

1 引言

惯性约束聚变(Inertial Confinement Fusion，ICF)是实现受控热核反应的一种方法，其驱动方式主要有高功率激光驱动、电子束驱动、轻离子束驱动和重离子束驱动。目前研究较为广泛、进展较快、技术较成熟的驱动方式是高功率激光驱动。用于ICF的高功率激光驱动器是一个庞大而又复杂的精密光学系统，其对光学元件的要求无论是从质量上讲还是从数量上讲都是空前的[1]。为了获得尽可能高的传输效率和尽可能好的光束质量，ICF系统对光学元件的波面误差提出了苛刻的要求[2]，其中包括空间尺度大于33 mm的低频波面误差和空间尺度介于2.5～33 mm之间的中频PSD1波面误差[3,4]。

以美国“国家点火装置”(National Ignition Facility，NIF)为例，该装置的高功率激光驱动器使用了数千件通光口径大于42 cm×42 cm的大口径平面光学元件，大部分为矩形光学元件[5]，其中一部分光学元件在使用角度下的反射波前误差要予以严格控制，如：大口径偏振片，其使用角度为57°，外形尺寸为810 mm×430 mm×90 mm；大口径传输反射镜，其使用角度为45°，表面镀有高反射率的介质膜，外形尺寸为610 mm×440 mm×85 mm，设计要求这两类元件在使用角度下的反射波前误差PV值优于λ/3(λ=632.8 nm)、PSD1(Power Spectral Density)优于1.8 nm[6]。

在测量上述光学元件的波前误差时，由于受到干涉仪测量口径的限制，不得不考虑使用较大的测量角度来保证干涉仪的有效测量口径能够覆盖待测光学元件的通光口径。此外，部分镀膜元件在使用角度下对测量光源的反射率较低，导致干涉仪无法获取满足要求的干涉图像，必须调整测量角度，以获得满足对比度要求的干涉条纹图像。这两种情况都将导致测量角度和实际使用角度发生偏差，不能直接获得使用角度下的反射波前误差。通常采用经典插值算法测量使用角度下的反射波前畸变，但该方法对中频波前测量将会产生较大误差[7-8]。为解决因测量角度和使用角度不同导致的测量误差，以及经典插值算法引入的中频波前测量误差，本文提出了将测量角度下的反射波前转换到使用角度下的波前，给出了换算及恢复方法，并针对该方法开展了误差分析和实验验证。

2 测量原理

2.1 斜入射角度下的反射波前测量分析

图1是斜入射测量角度下的波面误差检测示意图。由干涉仪出射的准直光束在通过标准参考面时分为两束，一束由标准透射镜反射形成标准参考光束，另一束光以θ角度入射到待检光学元件表面并反射，再由标准反射镜反射沿原路返回形成测试光束。标准参考光束与测试光束干涉形成干涉条纹，再采用波长移相技术，产生多幅移相干涉图，用计算机控制CCD(Charge Coupled Device)摄像机对干涉条纹进行采样，对数据进行分析和处理后可得到光学元件在此测量角度下的反射波前畸变信息[9-10]。但是如果该待测元件的摆放角度即入射测量角度θ不是待测元件在实际强激光装置系统中的使用角度，就需要通过转换计算得到使用角度下的波前畸变[11]。

图1 斜入射角度下的反射波前测量示意图Fig.1 Measurement method for reflective wavefront error in oblique incident situation

从图1中可以看出，假设待测表面面形高度为h，干涉仪出射光束的入射角为θ，此时干涉仪测量得到的待测元件反射波前畸变为φ：

φ=a+b=a+acos 2θ=h/cosθ(1+cos 2θ)=

h/cosθ(2cos2θ)=2hcosθ.

(1)

由上可知，如果定义θ2为待测元件的实际使用角度，定义θ1为干涉仪斜入射的测量角度，那么存在如下的余弦换算关系式：

φ2=φ1cosθ2/cosθ1.

(2)

例如，待测元件在垂直入射，即θ1=0的情况下，干涉仪测量得到的反射波前数据为φ1，那么待测元件在实际使用角度45°下的反射波前φ2=φ1cos 45°。

由图1所示的测量光路图可知，在干涉仪斜入射测量的情况下，不仅两个不同入射角度下的波前畸变存在余弦变换关系，在波面的横向尺寸上也对应存在着余弦关系，而纵向尺寸保持不变。假设在入射角为θ1的情况下测量得到的波面横向尺寸为x1，纵向尺寸为y1，在入射角为θ2的情况下测量得到的波面横向尺寸为x2，纵向尺寸为y2，则有下面的换算关系：

x2=x1cosθ2/cosθ1，y2=y1,

(3)

所以由测量角度下的波前畸变换算到使用角度下的波前畸变的计算过程如图2所示。

图2 测量角度下的波前换算到使用角度下的波前计算框图Fig.2 Conversion steps of reflective wavefront error from measurement angle to use angle

由上可知，不同角度下的波面数据存在缩放关系，为了获得与干涉仪测量空间分辨率相同的波面数据，对干涉仪测量角度下的波面数据φ1进行位相校正和长度校正后，可以得到φ2和x2，再使用双三次插值(Bicubic interpolation)方法对经过位相校正后的波面数据φ2进行插值处理，最后可以得到使用角度下的波面数据。

2.2 双三次插值算法对中频误差的影响分析

双三次插值又称立方卷积插值[12]，是一种高精度的插值方式，该算法利用待采样点周围16个点的位相值作三次插值，不仅考虑到4个直接相邻点位相的影响，而且考虑到各邻点间位相值变化率的影响，三次运算可以得到更高分辨率的波面数据。插值算法的计算公式如下[13]：

Φ2(m,n)=A×B×C,

(4)

A=[S(1+u)S(u)S(1-u)S(2-u)],

(5)

(6)

C=[S(1+v)S(v)S(1-v)S(2-v)]T,

(7)

其中：m，n分别表示Φ2(m,n)矩阵行数和列数的下标，m=1,2,3…y2，n=1,2,3…x2。i=fix(my1/y2)+2；j=fix(nx1/x2)+2，fix表示取整函数；u=my1/y2-fix(my1/y2),u表示小数部分；v=nx1/x2-fix(nx1/x2)表示小数部分。

S(x)表示双三次插值基函数，数学表达式见式(8)。

(8)

为了分析双三次插值算法本身在插值计算过程中对波面中频段误差造成的影响，选择口径为363 mm×363 mm的波面数据作为原始数据，如图3所示。

图3 原始波面数据(PV=0.08λ， RMS=0.013λ， PSD1=0.74 nm)Fig.3 Original wavefront error(PV=0.08λ， RMS=0.013λ， PSD1=0.74 nm)

对该波面数据仅进行水平方向上的插值压缩，使数据口径横向变为363cos45°mm，纵向保持363 mm不变，利用上述的双三次插值算法计算后得到的波面数据如图4所示。

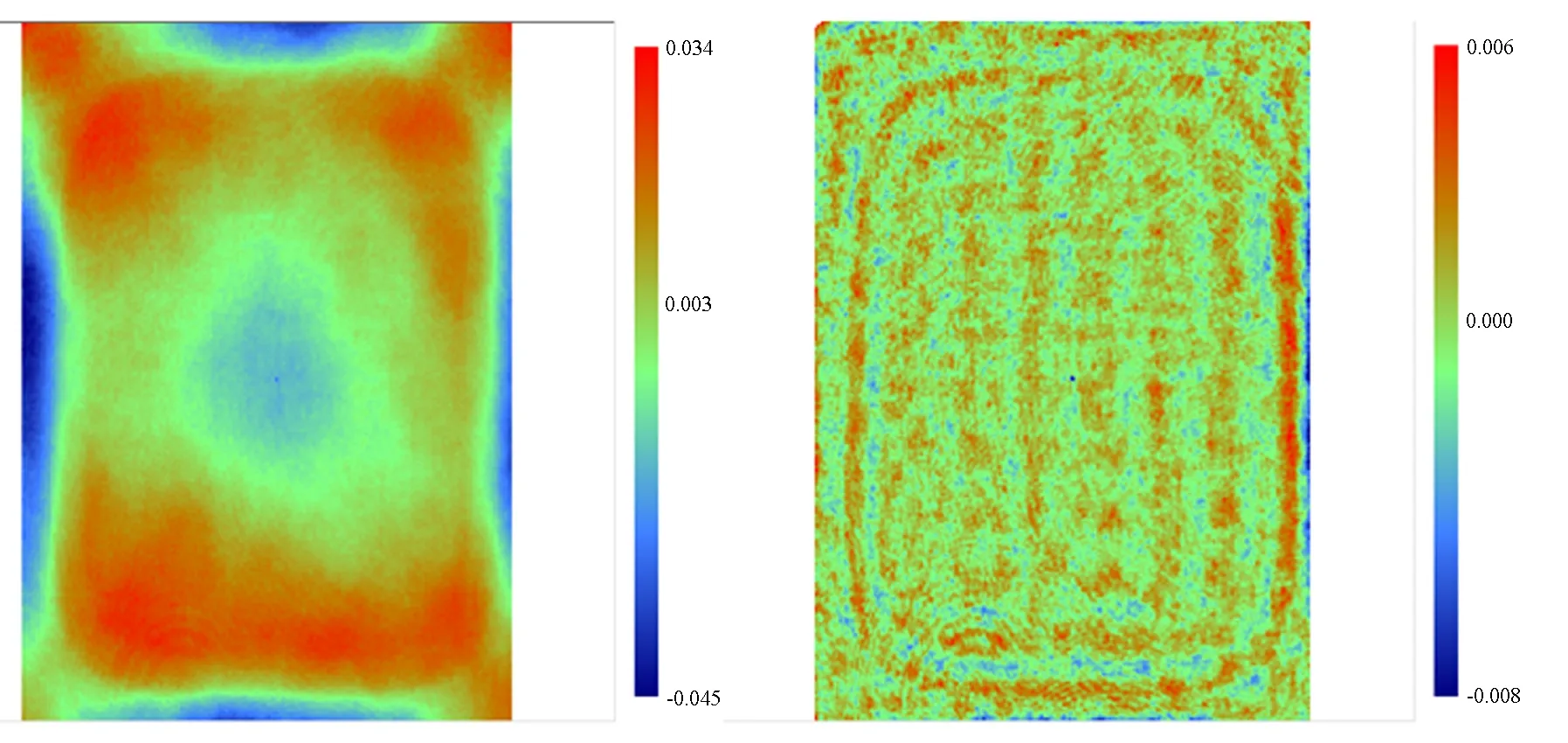
图4 压缩后的波面数据(PV=0.08λ，RMS=0.013λ，PSD1=0.83 nm)Fig.4 Compressed wavefront error(PV=0.08λ， RMS=0.013λ， PSD1=0.83 nm)

比较图3和图4可知，原始波面数据的PSD1和插值后波面数据的PSD1差值为0.09 nm，PV和RMS基本不变，这说明插值计算过程对中频段PSD1的误差小于0.1 nm，基本不会对测量波面的中频造成影响。

在上面的计算过程中，仅选择了45°的压缩量，而在实际测量过程中，测量角度与使用角度的差在0°到70°之间，最大为70°。如果角度差变大，则与之相对应的横向插值的数据量也要变大，那么不同角度差的插值计算过程对PSD1的影响也不相同。

利用上述的原始波面数据，在插值计算过程中选择不同的压缩角度进行插值，即10°，20°，30°，40°，50°，60°，70°，计算每个角度插值后波面的PSD1与0°原始波面数据PSD1值的差，得到如图5所示的结果。

从图5曲线可知，角度变化量在60°以内，双三次插值算法对中频PSD1的计算误差小于0.4 nm，这就要求光学元件在干涉仪上的实际摆放测量角度应该与使用角度之间的角度差小于60°。

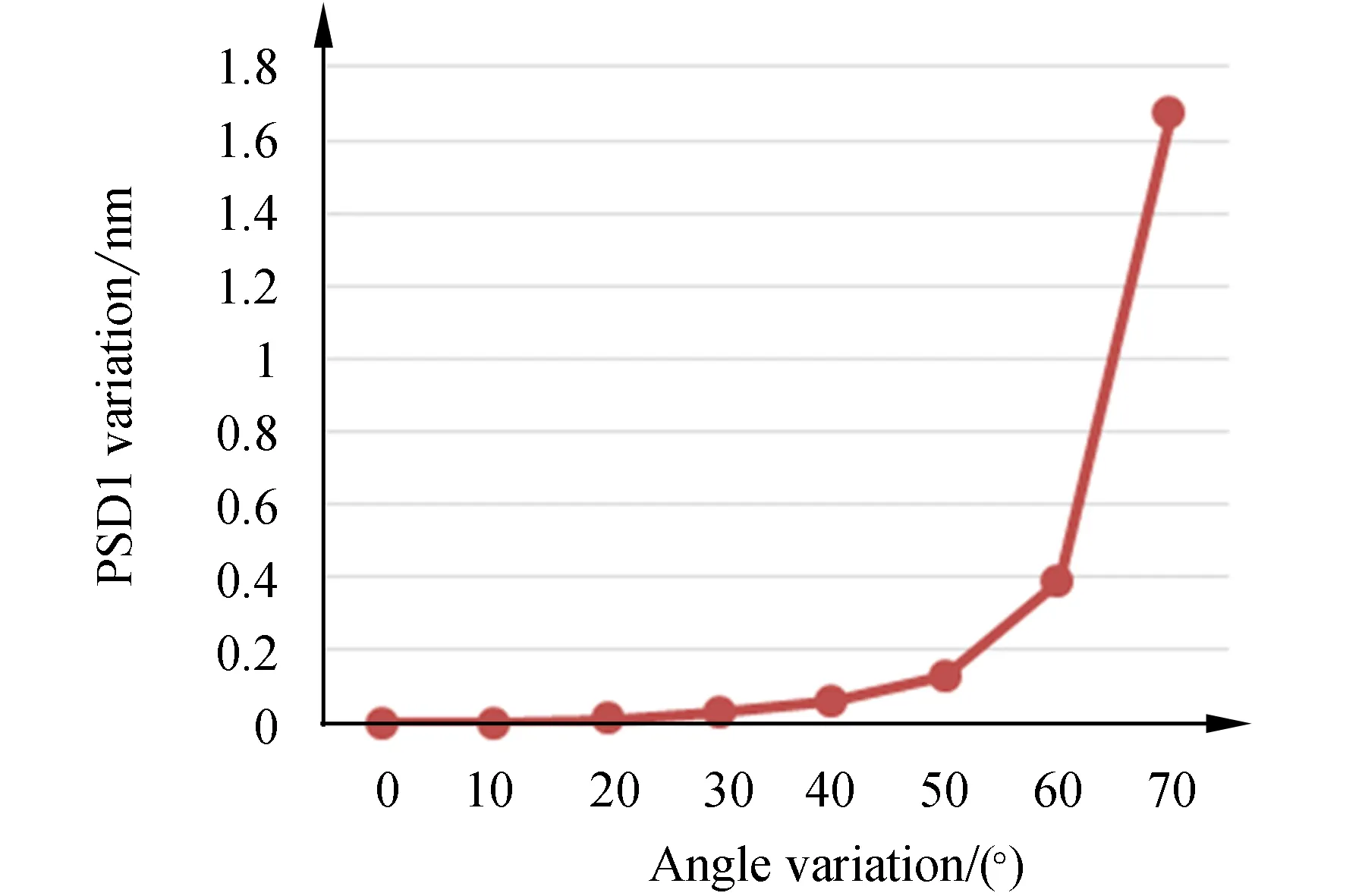
图5 插值算法引起的PSD1变化量与测量角度变化量的关系Fig.5 Relationship of PSD1 variation and measurement angle variation caused by interpolation algorithm

3 实验结果与讨论

实验中使用的是ZYGO大口径波长移相平面激光干涉仪，输出波长为632.8 nm，有效口径为Φ600 mm，CCD分辨率为1 000 pixel×1 000 pixel，干涉仪标准镜的PV值优于λ/12。待测元件为有效口径是400 mm×400 mm的熔石英反射镜基板。该玻璃的口径小于干涉仪测量口径，并带有明显的中频误差痕迹特征。实验中，首先进行垂直入射，得到0°下的反射波前数据，然后通过余弦换算和双三次插值算法计算得到45°反射波前，最后在干涉仪工作平台上直接测量45°反射波前，并把该结果作为标准数据与本文方法得到的数据进行比较，以定量分析余弦换算和双三次插值算法的计算误差。

熔石英反射镜垂直入射得到0°下的反射波前数据，如图6所示。

图6 0°反射波前误差(PV=0.46λ， RMS=0.093λ， PSD1=1.5 nm)Fig.6 0°reflective wavefront error(PV=0.46λ， RMS=0.093λ， PSD1=1.5 nm)

通过余弦变换和双三次插值后计算得到的45°反射波前数据，如图7所示。

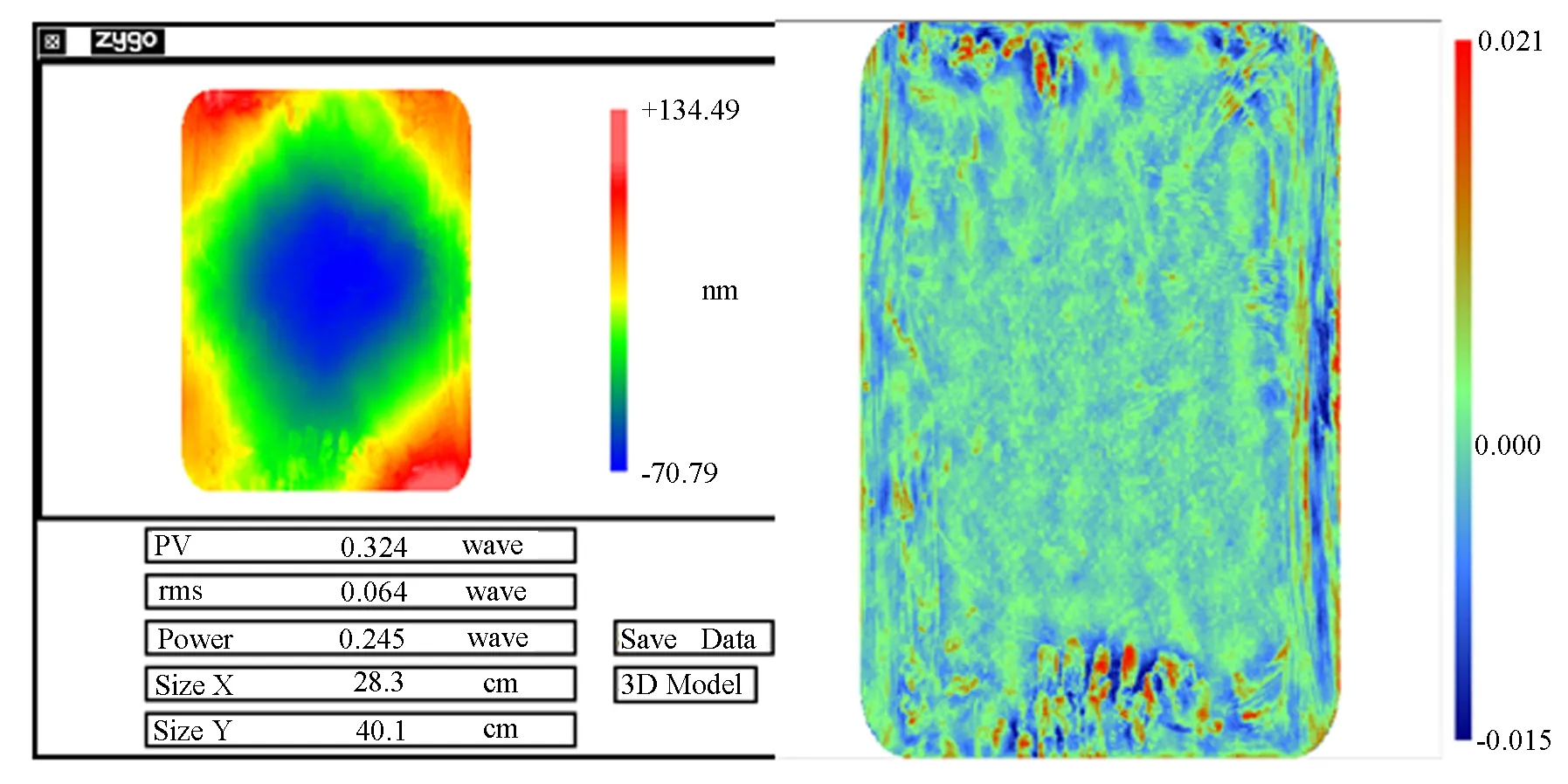
图7 0°换算到45°反射波前的误差(PV=0.32λ， RMS=0.064λ， PSD1=2.41 nm)Fig.7 Measuring results by converting 0°reflective wavefront to 45° (PV=0.32λ， RMS=0.064λ， PSD1=2.41 nm)

在干涉仪上直接测量45°反射波前的标准数据如图8所示。

比较图7与图8可知，两者PV值相差0.01λ，RMS相差0.003λ，PSD1相差0.08 nm。实验表明非使用角度下的测量结果经过余弦换算和双三次插值算法后，能够准确计算得到实际使用角度下反射波前的低频和中频PSD1的数据。

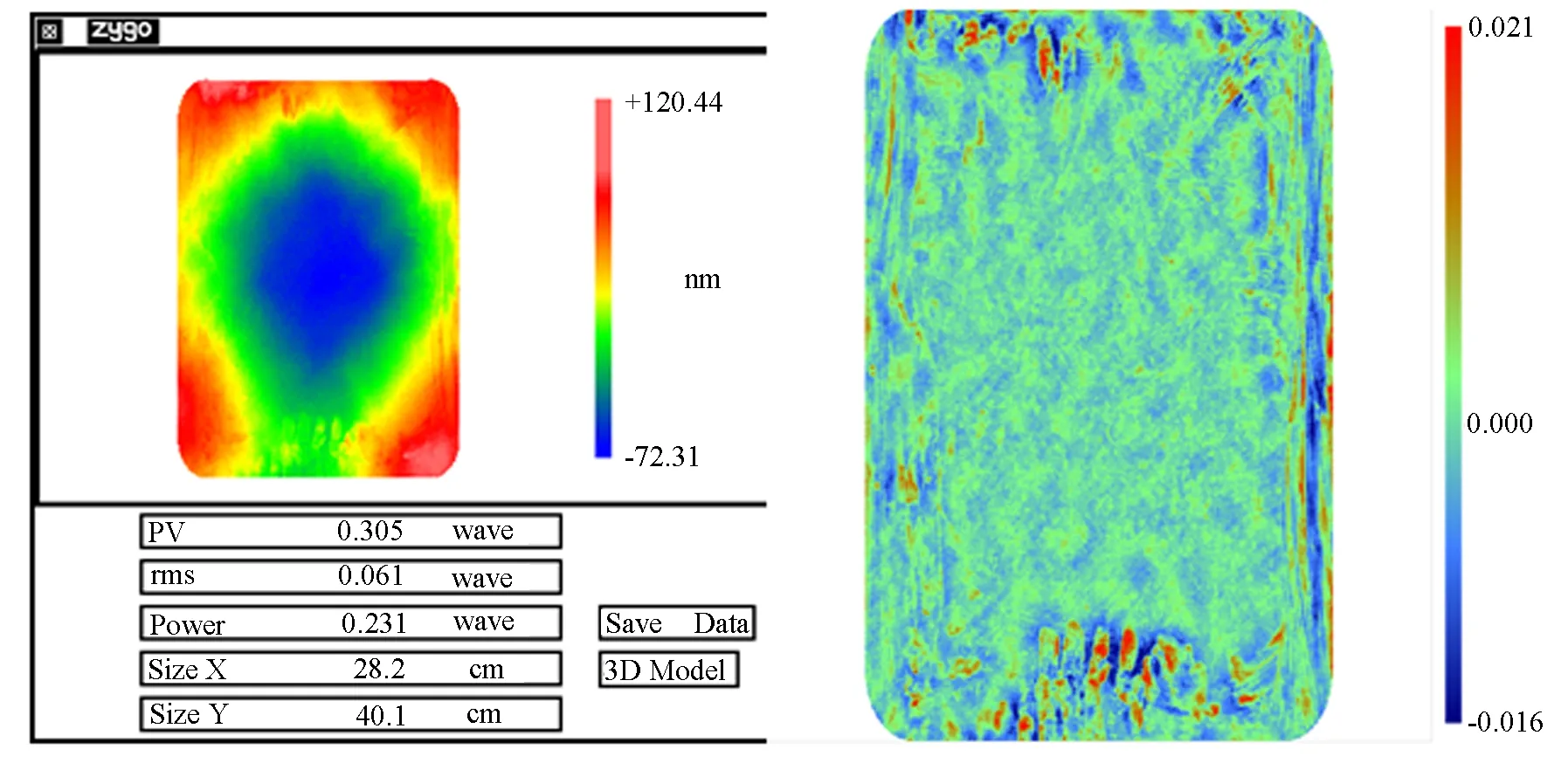
图8 直接测量45°反射波前(PV=0.31λ， RMS=0.061λ， PSD1=2.33 nm)Fig.8 0°wavefront error at 45°reflective angle(PV=0.31λ， RMS=0.061λ， PSD1=2.33 nm)

4 结论

本文首先对斜入射测量角度下的波前转换到使用角度下波前的余弦换算过程进行了分析，得到了实际测量角度与实际使用角度下波前误差的计算关系；然后对双三次插值算法本身引起的中频PSD1误差进行了分析。从分析结果可见:光学元件在干涉仪上的实际测量角度与使用角度之间的角度差应小于60°，所以在能够满足有效测量口径的情况下，入射角度应该与实际使用角度尽可能的接近。最后以400 mm×400 mm的熔石英反射镜为研究对象，通过实验验证了在垂直入射下的0°反射波前转换到45°反射波面的数据和直接测量45°反射波前数据的一致性。结果显示：两者PV值相差0.01λ，RMS相差0.003λ，PSD1相差0.08 nm。这也说明本文提出的余弦换算和双三次插值算法可以应用于高功率激光装置中大口径光学元件实际使用角度下的反射波前畸变测量。

[1] WOLFE C R, LAWSON J K. The measurement and analysis of wavefront structure from large aperture ICF optics[R].OfficeofScientific&TechnicalInformationTechnicalReports, 1995, 2633:361-385.

[2] ENGLISH R E, LAUMANN C W, MILLER J L,etal.. Optical system design of the National Ignition Facility[C].InternationalOpticalDesignConference, 1998,726.

[3] 许乔,顾元元,柴林，等. 大口径光学元件波前功率谱密度检测[J]. 光学学报，2001，21(3):344-347. XU Q, GU Y Y, CHAI L,etal.. Measurement of wavefront power spectral density of large optical components[J].ActaOpticaSinica,2001,21(3):344-347. (in Chinese)

[4] LIU SH J, JIN CH X,ZHOU Y,etal.. Investigation on measurement of mid-frequency wavefront error for large optics in high-power laser system[C].ConferenceonOpticalMeasurementSystemforIndustrialInspectionIX,2015.

[5] BAISDEN P A,ATHERTON L J,HAWLEY R A,etal.. Large optics for the national ignition facility [J].FusionScienceandTechnology,2016, 69: 295-351.

[6] 朱硕，张晓辉. 误差分离技术在平面镜瑞奇-康芒法检测中的应用[J]. 光学精密工程，2014，22(1):7-12. ZHU SH, ZHANG X H. Application of error detaching to Ritchey-Common test for flat mirrors [J].Opt.PrecisionEng.,2014, 22(1):7-12. (in Chinese)

[7] 朱硕，张晓辉. 瑞奇-康芒式大口径平面镜面形数据处理方法对比研究[J]. 应用光学,2015，36(5):698-704. ZHU SH, ZHANG X H. Comparative study on data processing method for large flat mirror in Ritchey-Common test[J].JounalofAppliedOptics,2015,36(5):698-704. (in Chinese)

[8] 姜涛，杨炜，郭隐彪. 基于经验模态分解-Wigner分布的光学元件中频误差识别[J]. 强激光与粒子束,2014，26(3):032003-1-032003-7. JIANG T, YANG W, GUO Y B,etal.. Mid-spatial frequency error identification of precision optical surface based on empirical mode decomposition-Wigner-Ville distribution[J].HighPowerLaserandParticalBeams, 2014, 26(3):032003-1-032003-7. (in Chinese)

[9] de GROOT P. Principles of interference microscopy for the measurement of surface topography[J].AdvancesinOpticsandPhotonics,2015, 7:1-65.

[10] 马春桃，罗红心，王劼,等.斜入射法检测平面反射镜的面形误差[J]. 激光与光电子学进展，2011(7):071201-1-071201-7. MA CH T, LUO H X, WANG J,etal.. Surface error measurement of plane mirrors based on oblique incidence[J].Laser&OptoelectronicsProgress,2011(7):071201-1-071201-7. (in Chinese)

[11] 刘兆栋，陈磊，韩志刚. 斜入射干涉检测大口径碳化硅平面反射镜[J]. 光学精密工程，2011，19(7):1437-1444. LIU ZH D, CHEN L, HAN ZH G. Measurement of large aperture SiC flat mirrors by oblique incidence interferometry[J].Opt.PrecisionEng.,2011, 19(7):1437-1444. (in Chinese)

[12] QU Y SH, TIAN W J, LI Y C,etal.. Improvement of the space resolution of the optical remote sensing image by the wavelet bi-cubic interpolation[J].ActaPhotonicaSinica, 2004, 33(5):601-604.

[13] 王会鹏, 周利莉, 张杰. 一种基于区域的双三次图像插值算法[J]. 计算机工程，2010，36(19):216-218. WANG H P, ZHOU L L, ZHANG J. Region-based bicubic image interpolation algorithm [J].ComputerEngineering, 2010, 36(19):216-218. (in Chinese)

Measurement and calculation for reflective wavefront error of large optics at oblique incidence

XU Long-bo1,3, ZHOU You2, ZHU Ri-hong1, LIU Shi-jie2*，ZHENG Wan-guo4

(1.CollegeofElectronEngineeringandPhotoelectronicTechnologyNanjingUniversityofScienceandTechnology,Nanjing210094,China; 2.KeyLaboratoryofMaterialsforHighPowerLaser,ChinaAcademyofSciences,Shanghai201800,China; 3.ChinaAcademyofEngineeringPhysics,Mianyang621999,China; 4.ResearchCenterofLaserFusion,ChinaAcademyofEngineeringPhysics,Mianyang621999,China) *Correspondingauthor,E-mail:shijieliu@siom.ac.cn

The difference between the measurement angle and the use angle will produce measuring errors when the wavefront errors of the large reflective optics in a high power driving device are measured. So this paper proposes a method to convert the reflection wavefront in a measuring angle into the reflection wavefront in a use angle. Firstly, the cosine conversion method used in conversing the wavefront in an oblique incidence angle into the wavefront in the use angle was analyzed, and the calculation relationship of the wavefront errors between actual measurement angle and actual use angle was obtained. Then, the mid-frequency PSD1 (Power Spectral Density) error caused by the third interpolation algorithm itself was calculated, and it points out that the selected incident angle should be close to that the actual use angle as much as possible when the measuring condition meets the effective diameter measurement. Finally, the error analysis and experimental verification were carried out based on a 410 mm ×410 mm fused quartz reflector.Using this method, the 0° reflection wavefront was convered into the 45° reflection wavefront, and the measuring result after conversion was compared with that of the direction measuring result at 45°. The compared results show that the differences of PV values, RMS values and the PSD1 values are 0.01 λ, 0.003 λ and 0.08 nm, respectively. These results indicate that the method not only can calculate exactly the low frequency errors of reflection wavefront, but also can obtain the PSD1 mid-frequency error.

high power laser device; large optics; reflection wavefront; wavefront error; bicubic interpolation; mid-low frequency error

2016-10-26；

2016-11-17.

国家自然科学基金青年科学基金资助项目(No.11602280)

1004-924X(2016)12-3027-06

TH703

:Adoi:10.3788/OPE.20162412.3027