周期叠加外延—最近邻抽样回归组合模型在韩江流域年径流预测中的应用
2016-02-11李俊伟
李俊伟
(广东省水文局汕头水文分局,广东 汕头 515041)
周期叠加外延—最近邻抽样回归组合模型在韩江流域年径流预测中的应用
李俊伟
(广东省水文局汕头水文分局,广东 汕头 515041)
为提高年径流预报精度,尝试将周期叠加外延法与最近邻抽样回归模型结合,用韩江流域潮安站年径流系列作试验,结果表明组合模型预测合格率比单一周期叠加外延模型高,预测效果较好。
韩江;周期叠加外延模型;最近邻抽样回归模型;组合;年径流
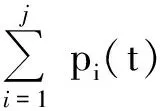
1 周期分析识别及外延预测
1.1 周期分析
周期分析有频谱分析、小波分析、最大熵谱方法、方差分析等多种方法。本文用方差分析来识别周期性。一般而言,如果某一要素存在周期性变化,那么按其存在周期分组排列时,处于同一组内的各个数据应该是同一位相下的观测值,不同组的数据为不同位相下的观测值,在各个周期高峰时期的观测值平均来说比较大,在各低谷时期的观测值比较小,峰谷之间的转换时期是中等的,因此在同组内的数据差异相对较小,组与组之间的差异较大。反之,如果不按其周期分组排列时,则同组内的数据相差较大,组间数据相差较小。组间与组内差异的情况,可分别用计算离差平方和的方法将其反映出来,并且把它们进行比较,从而判断序列是否有周期存在,这就是用方差分析作周期性分析的基本原理[1]。
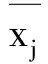
1.2 周期叠加外延模型
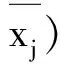
2 单因子最近邻抽样回归(NNBR)
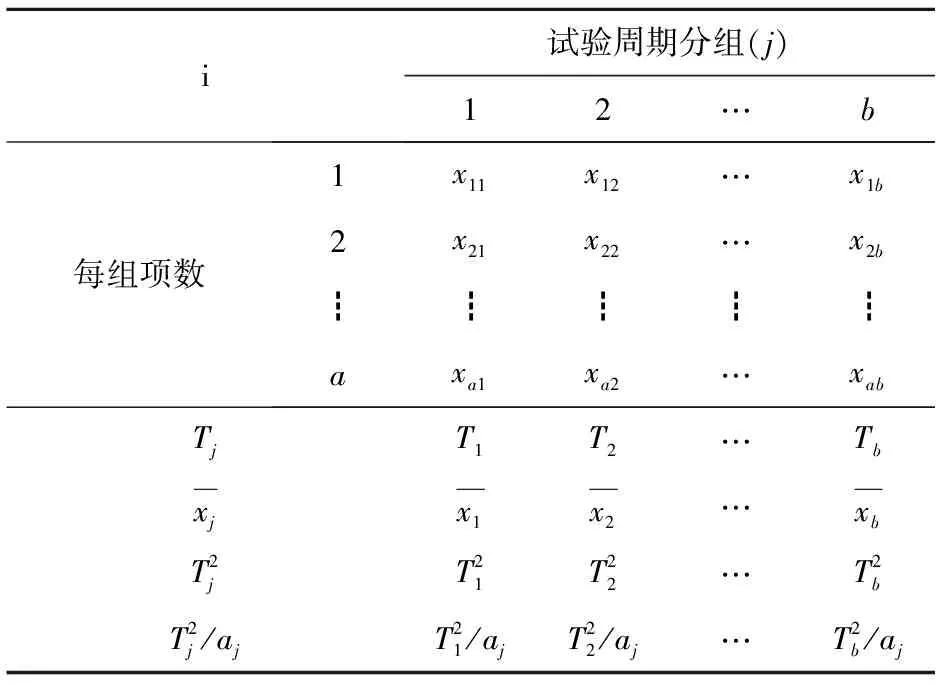
表1 试验周期分组排列
2.1 基本原理
最近邻抽样回归模型是一类基于数据驱动的、不需识别参数的非参数模型。该模型认为客观世界的发生发展存在一定联系,未来的运动轨迹与历史具有相似性,即未来发展模式可以从已知众多模式中去寻求[2]。根据研究对象不同,NNBR模型分为单因子NNBR模型和多因子NNBR模型两种形式。本文采用单因子NNBR模型。
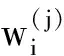
(1)
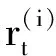
根据上述思想,单因子NNBR模型的基本形式有:
(2)
2.2 最近邻数K、特征量量维数P的确定
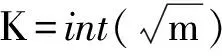
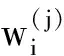
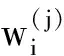
(3)
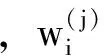
3 周期叠加外延法—最近邻抽样回归组合模型预测步骤
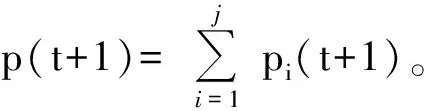
2) 对残差序列建立最近邻抽样回归模型得到ε(t+1)。
4 周期叠加外延—最近邻抽样回归组合模型在韩江年径流预测中的应用
韩江是广东省第二大河流,发源于广东省紫金县的七星崠,上游称琴江,流至五华水寨后称梅江,由西南向东北流经五华、兴宁、梅县至大埔县的三河坝与由福建省来的汀江汇合后称韩江。折向南流,至潮州市以下三角洲河网区,分北、东、西溪经汕头市入南海。干流全长为470km,流域集雨面积为30 112km2,河道平均坡降为0.4‰。韩江流域属亚热带气候,气候温和多雨,受海洋性东南季风影响很大,雨洪主要集中于夏季。流域内降雨量充沛,但时空分布不均,多年平均降雨量在1 400~1 700mm,年内分配不均匀,其中4—9月降雨量占全年降雨量的70%以上,5、6月更为集中。本流域水量丰富,据潮安水文站55a(1951—2005年)资料统计,该流域多年平均年径流量为248.8 亿m3,年径流模数为27.0L/(s·km2),且年径流量年际变幅大,年径流量离散程度Cv为0.31。
对韩江潮安站1951—2005年年径流系列,进行周期叠加外延法—最近邻抽样回归预报。
以1951—2000年资料作为建模样本,2001年资料作为检验样本。
1) 周期稳定性分析。判别周期稳定性一般做法是检查要用以预报的周期在预测年份前近几年的情况,如果比较稳定,则采用。以1951—1999年的资料系列作周期分析,在α=0.05下,第一周期长度T=22,方差比F=3.162673>F(α)=1.96;第二周期长度7,方差比F=3.714432>F(α)=2.32;第三周期长度8,方差比F=2.597718>F(α)=2.24。再以1951—2000年的资料系列作周期分析,得到的周期长度也是22a、7a、8a,对应的周期振幅也相对稳定。可见在近期,周期较稳定。
2) 外延预测。建模样本经过周期叠加外延模型提取周期,得到2001年第一周期值为241.6,第二周期值为31.6,第三周期值为22.5,则p(2001)=241.6+31.6+22.5=295.7亿m3。
3) 对残差序列建立最近邻抽样回归模型。应用单因子最近邻抽样回归模型对年径流量序列与历年提取出来的3个周期波叠加之差进行模拟计算,根据尝试,取K=3,P=3。
由前50个数据构造特征矢量Dt(t=4, 5, …,,50),共有47 个特征矢量,经过计算,与当前特征矢量D50最近邻的3个特征矢量为:D38=(-18.68,-6.68,-51.34),D28=(-3.13, 9.99,-44.58),D43=(3.42, 23.76,-32.17);相应的欧氏距离分别为r38=33.00,r28=34.58,r43=45.56;相应的后续值分别为-38.94,-17.06,-22.86;权重分别为r38=0.5454,r28=0.2727,r43=0.1818。预测2001年残差的值为-30.0亿m3。
于是最后预测2001年的径流量为295.7+(-30.0)=265.7 亿m3,实测为277.9 亿m3。
同理,采用逐步向下滑动预报的方式,用1951—2001年资料预测2002年,周期叠加外延模型预测值为173.6,残差序列最近邻抽样回归模型取K=3,P=3,与当前特征矢量D51最近邻的3个特征矢量为D27、D50及D45,相应的欧氏距离分别为r27=22.32、r50=23.37及r45=32.65,相应的后续值分别为-25.63、-56.18及27.24,权重不变,预测2002年残差的值为-24.35亿m3,则2002年的最终预测值为149.3亿m3;依此类推,一直预测到2005年,结果如表2。作为对比,把单一周期叠加外延模型与组合模型预测结果列于表2及图1。许可误差按《水文情报预报规范(GB22482—2008—T)》中规定的多年变幅的20%[4]。
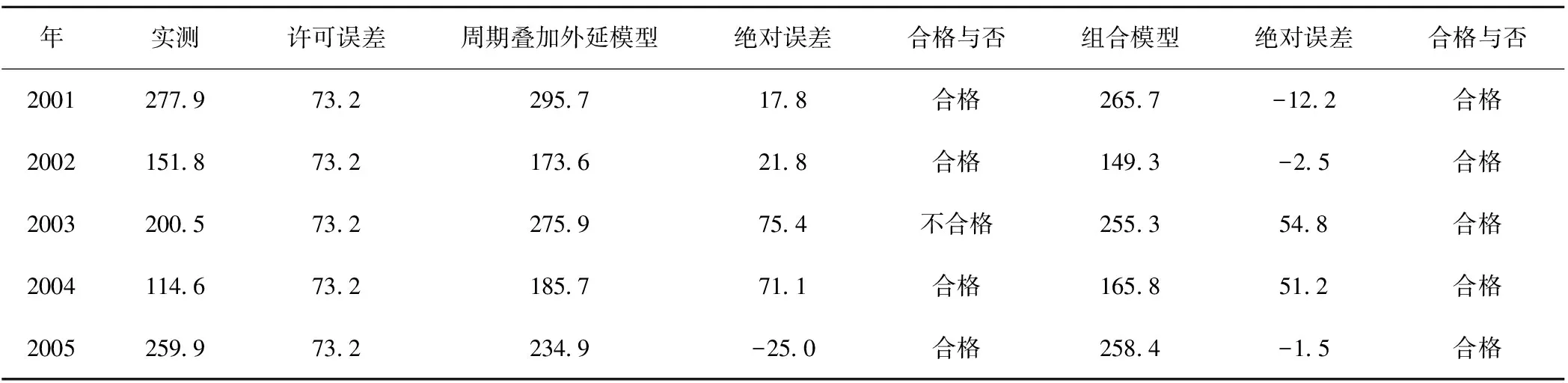
表2 周期叠加外延模型与组合模型预测结果比较 亿m3
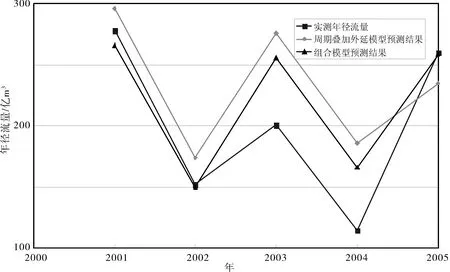
图1 周期叠加外延模型与组合模型预测结果比较示意
从表2及图1看出,组合模型预测合格率比单一周期叠加外延模型高,绝对误差小,预测值与实测值更接近。
5 结语
年径流有多种预测方法,本文采用周期叠加—最近邻抽样回归组合模型对韩江潮安水文站年径流序列进行预测,结果表明组合模型预测精度比单一周期叠加外延模型高。该组合模型对单一模型所舍弃的有用信息进行再利用,结构更合理,故预测效果好,实用性强。不足之处在于无论是周期叠加外延模型还是最近邻抽样回归模型都是基于历史会重演的假设上,但水文要素的变化不会按照固定的周期循环反复,如若以潮安站1951—1987年及1951—1988年年径流量作周期分析,这2个序列均只存有1个周期(8a期),与上面提到的1951—1999年及1951—2000年的序列存有3个周期(22a期、7a期、8a期)有差异。可见由某时期分析得到的结果只能作为一段时间内的预报依据,不能无限地外推下去,当未来的运动轨迹超出了它本身具有的由历史资料获得的规律时,该模型就无能为力了。
[1] 范钟秀.中长期水文预报[M].南京:河海大学出版社,1999.
[2] 王文圣,袁鹏,丁晶. 最近邻抽样回归模型在水环境中的应用[J].中国环境科学,2001,21(4):367-370.
[3] 刘治理,马光文,严秉忠. 最近邻—径向基函数网络模型在日径流预测中的应用[J].广东水利水电,2005(3):8-10.
[4] 水文情报预报规范:GB22482—2008—T[S].
(本文责任编辑 马克俊)
Periodic Extensional—Nearest Neighbor Bootstrapping Regressive Combinatorial Model in Annual Runoff Prediction of Hanjiang River
LI Junwei
(Bureau of Hydrology of Shantou, Guangdong Province, Shantou 515041,China)
In this paper, Periodic Extensional Model is experimented to combine with Nearest Neighbor Bootstrapping Regressive Model in order to improve the accuracy of annual runoff prediction. In the case of Chao’an Hydrological Station of Beijiang River, experiment results show that the annual runoff time series data of Hanjiang river basin prediction model is developed.The fitting result is more satisfactory than that of the Periodic Extensional model.
Hanjiang River; periodic extensional model; nearest neighbor bootstrapping regressive model; combinatorial model; annual runoff
2016-04-15;
2016-11-13
李俊伟(1975),男,本科,高级工程师,主要从事水文水情工作。
P338
:A
:1008-0112(2016)012-0001-04
