数学建模应用于土木工程土方调配刍议

2016-02-11刘军

工程技术研究 2016年12期

关键词：运距假想方格

刘军

（安徽理工大学土木建筑学院，安徽淮南 232001）

数学建模应用于土木工程土方调配刍议

刘军

（安徽理工大学土木建筑学院，安徽淮南 232001）

大型土方工程施工中，可利用运筹学当中的线性规划知识，构建数学模型，通过进行多次运算步骤操作之后，最终确定运距最短的土方调配相应最优方案。并作为施工指导，以此实现成本降低，获取更好经济效益。

数学建模；土方调配；线性规划

在土木建筑工程大型化的土方施工过程中，为实现工程造价及成本降低，通常需在施工开展前，制定完备的土方调配方案，以此为施工提供指导。而在现实施工中，诸多工程施工人员在方案制定时，仅凭借自身一些经验和尝试进行抉择。当然，凭借以往经验优势确实可以获取较为满意的方案，但如若问题比较复杂，仅仅凭借自身常识与经验，则会存有较大困难。而通过运筹学当中有关线性规划方面的知识，便能够以一种较为简单的方式，获取目标明确的最佳方案。文章以实际案例方式，构建数学模型，运用线性规划知识，对土方调配相应最佳方案的求解方法予以给出，即表上作业法。

1 构建数学模型

1.1 编制土方调配表

土方调配表见表1，表格当中的表示待求的土方调运量，从第个挖方区向第个填方区调运的土方量。如乃是挖方区向填方区调运的土方量，表格内最右边的数值，乃是调配区所具有的实际运距。

表1 土方调配表

1.2 构建数学模型

目标函数：

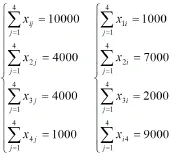
由所构建的数学可行得知，此问题实际上是一个有关线性规划的问题。可采用单纯形法进行求解，但是运用此方法实施求解，则需针对各约束方程，外加一个对应的人工变量，最终构成求解4+4个约束，一共包括有4×4＋4＋4各变量的问题。此种解题思路，具有十分大的工作量。通过观察模型得知，此模型具有一定特殊性，全部4个约束方程，均仅为各个变量的综合。也就是在约束方程当中的各个变量所存有的对应系数，不“1”则为“0”，因此，在这里可不将人工变量引入其中，而运用一种同样特殊的表上作业法，实施求解操作。

2 初始调配方案编制

制定初始方案中，选用有限具有最小运距的调配区实施调配。基于此原则，可促使目标函数在具体的运算次数方面的减少。①通过上述表1可知，未知量具有最小的运距，因从当中调运1000m3至也就是=1000m3，因已经得到相应足土方，故和则不同给予土方，即可得到与之对应的方格当中则可填写成0；②然后再选择一个最小运距的方格实施调配操作，在没有进行调配的方格当中，最小的运距则为由此便可得出，=1000m3，即=0；③对上述步骤进行重复操作，每次均对最小运距的方格实施相应调配操作。依据具体的供需需求，对此方格相应需求尽可能给予满足，且依次将其它求出，也就可将初始调配方案得出。

3 调配方案最优化检验

依据对最小运距进行优先选择的原则，因此，所获取的最小目标函数值，不能保证其是最小的，所以需对其实施检验。制定一个假想运距，假想运距乃是整个假定方案当中最优时候的虚拟运距。在相应假想运距条件下，任意调整方案，但是其目标函数值S不发生改变。所以当原运距都等于或者大于与之处于对应状态的假想运距时，则此时的目标函数值，便不能再次降低，所以此方案乃为最优。相反，当目标函数值仍然能够再次降低时，则方案并不是最优。