系统辨识中应用遗传算法的分析及研究*

2016-02-11佘明洪

工程技术研究 2016年12期

关键词：系统结构适应度遗传算法

佘明洪

（1.重庆电子工程职业学院，重庆 401331；2.重庆大学自动化学院，重庆 400044）

系统辨识中应用遗传算法的分析及研究*

佘明洪1，2

（1.重庆电子工程职业学院，重庆 401331；2.重庆大学自动化学院，重庆 400044）

文章首先阐述了系统辨识与遗传算法，随后对遗传算法在系统辨识中的具体应用进行论述。期望通过文章的研究能够对促进遗传算法在系统辨识中的推广应用有所帮助。

系统辨识；遗传算法；应用

1 系统辨识与遗传算法概述

1.1 系统辨识

系统辨识是指以输入和输出数据为基础，从某一类模型当中确定出一个与被测系统等价的模型。该定义中的关键要素有三个，即数据、模型和等价准则。可将系统辨识分为整体辨识和部分辨识。

1.2 遗传算法

遗传算法简称GA，是一种计算模型，能够通过模拟自然进化过程获取最优解。适应度是该方法最基本的搜索信息，不需要其它的辅助信息，由此使得GA成为智能计算的关键技术之一。GA具备全局性、高效性、并行性、鲁棒性、易扩展性、普适性、简明性等优点。

2 遗传算法在系统辨识中的具体应用

系统辨识的对象包括系统参数和系统结构。传统辨识方法仅能辨识其中一种，而GA可以辨识两种。

2.1 GA在系统参数辨识中的应用

运用GA对系统参数进行辨识的过程中，需要先建立一个模型，借助该模型将参数辨识问题转化为GA对模型参数的优化问题。利用二进制对各个参数进行编码处理，使其构成子串，随后以拼接的方式将子串构成“染色体”串。便于分析研究，可将系统描述成如下形式：

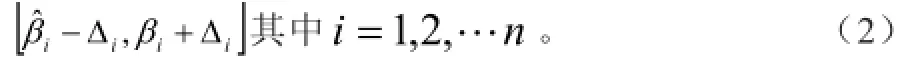
（3）确定适应度函数。估计的函数模型应当与实际数值的误差越小越好，而GA规定适应度函数的值越大，则表明该“染色体”的优越性越强。设该模型与已知实际值的误差平方和的倒数为最优模型估计的标准，由此可得适应度函数为经过计算，生成的“染色体”分别对应十进制值，随后从中找到使适应度达到最大的“染色体”，与之相对应的十进制数即为本次计算所得的最优解。最后采用多次循环的方法，便可获得最优模型。通过误差验证，遗传算法在系统参数辨识中具有较高的精确性。

2.2 GA在系统结构辨识中的应用

GA是一种模拟生物进化现象的优化方法，将定向与随机搜索有机结合，通过潜在解的群体实现全局寻找最优解的目标。GP是GA的扩展与延伸，它使用变长层次结构的程序树，克服了GA定长编码的局限性，有利于复杂问题的表述。GP在运算速度上也要优于GA。由于系统结构辨识是一个较为复杂的问题，因此可运用GP来解决此类问题，具体方法如下：

（1）生成初始个体。GP中的所有个体全部都是由算法树刻画的函数表达式，为便于动态修改，可将算法树视作为GP的对象。在初始个体生成的过程中，从F（函数集）中以均分、随机的方法选一个函数作为根节点，主要目的是为了生成具有层次化特点的复杂结构。当根节点选好之后，可以按照发出的线数，从F与终止符的并集当中，选出一个尾节点，此时算法树生成过程终止。

（2）生成初始群体。在GP中，初始群体的产生有两种方法，一种是生长法，深度优先；另一种是完全法，宽度优先。为使群体的形态更加丰富，搜索点能够最大限度地分布，可将两种方法结合，以此来生成初始群体。

（3）算子。在GP中的基本算子主要包括复制、交换与突变。复制是将上一代的优良个体带入到下一代群体当中，遵循优胜劣汰的原则；交换则是整个子树的交换，为避免交换过程中产生出巨形个体，必须使用树的最大允许深度对交换过程进行控制；在GP中，突变的作用较小，每一代个体中仅有5%左右会发生突变。

（4）辨识步骤。先确定出个体的表达方式，生成初始群体，执行相关的遗传操作，如复制、交换等，循环执行，直至达到终止条件。