基于自然贮存试验的产品贮存寿命评估方法

陈智芳，王俊华

(中国空空导弹研究院，河南 洛阳 471009)

基于自然贮存试验的产品贮存寿命评估方法

陈智芳，王俊华

(中国空空导弹研究院，河南 洛阳 471009)

为合理评估产品的贮存寿命，对贮存过程进行了研究，建立了贮存寿命的数学模型，给出了自然贮存试验方法，并提出了基于自然贮存试验数据的贮存寿命评估方法。结合某密封剂的自然贮存试验数据进行了实例应用，结果与实际情况基本一致，表明了该方法的合理性和实用性。

贮存寿命； 贮存过程； 数学模型； 自然贮存试验； 评估

0 引 言

贮存寿命为产品在规定的贮存条件下能够满足规定要求的时间长度[1]。

产品在规定的贮存条件下贮存时，处于不工作状态，且环境应力水平较低，故产品由于贮存而失效往往是一个非常缓慢的渐变过程，通常需要数年甚至数十年。

目前，贮存寿命主要通过加速寿命试验[2-4]、加速退化试验[5-7]以及相似产品类比分析法来分析评估。但由于加速试验条件的模拟程度不够全面、类比分析仅能提供粗略信息等原因，贮存寿命评估结果的可信度存在一定问题，尚需经过实际

贮存试验的验证。美国学者指出，确定导弹贮存寿命的唯一有效方法仍然是跟踪监测[8]。

为充分挖掘产品寿命潜力，合理规划翻修与报废工作，降低全寿命周期费用，对贮存寿命进行合理且可信的评估就很有必要。为此，本文在研究贮存过程的基础上，建立了贮存寿命的数学模型，并给出了基于自然贮存试验的贮存寿命评估方法，为合理评估产品贮存寿命提供了参考和借鉴。

1 贮存寿命的数学模型

一些产品(如导弹)出厂交付用户以后，大部分时间都贮存在库房中。贮存过程中，产品的性能会在环境应力的影响下逐渐发生变化，直至达到规定的性能下限。

设产品的性能参数为x，对应于某一时刻t的性能参数值为x(t)。长期贮存过程中，x(t)会随时间t的增加而逐渐退化，直至达到性能参数允许值x0，此时对应的时间为t0。

一般而言，选取t0作为贮存寿命。然而，对于批产品而言，每个产品的性能参数并不是完全一致的，而是呈现一定的波动性，服从某种类型的分布。如果选取t0作为贮存寿命就会存在一定的风险。考虑到实际应用时的可靠性和安全性，确定贮存寿命时，应使产品性能参数不差于x0，为此，需确定t0之前的某个时刻ts(ts≤t0)，使得

P(x(ts)≥x0)=R(t)

(1)

式中：ts为要求的贮存寿命；R(t)为贮存可靠度，一般取0.99或更大。

2 基于自然贮存试验的贮存寿命评估方法

在利用建立的数学模型对产品的贮存寿命进行评估时，需要借助产品贮存过程中的性能参数信息，为此，就要开展一定时间的自然贮存试验，获得该段时间内的产品性能参数信息，通过数理回归分析拟合得到产品的性能退化规律，进而对其贮存寿命进行评估。

2.1 产品自然贮存试验

开展自然贮存试验时，首先需对产品的规定贮存条件进行明确，并确保自然贮存试验条件与规定贮存条件一致。然后，选取检测合格的样品，在该试验条件下开展自然贮存试验。

自然贮存试验过程中，可设置m个检测点(即进行m次检测)，并定期(每年、每月或每天)进行检测，每次检测ni个样品。至试验结束时，可得到产品自然贮存试验过程中的性能参数个数为

(2)

2.2 产品性能退化规律的回归分析

由于贮存过程中各项环境条件基本稳定，使得产品性能退化规律通常可用线性关系(或经过某种变换之后呈线性关系)来描述，即产品的性能退化规律为

x(t)=kt+l+ε

(3)

式中：k，l为母体回归参数；ε为x(t)对母体回归线的残差。

工程实践中，测试数据往往有限，在独立、等精度测量情况下，可利用最小二乘法拟合得到回归直线：

x=at+b

(4)

式中：a,b为所拟直线的回归参数。

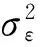
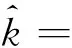
(5)

(6)

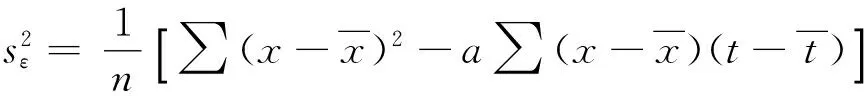
(7)

(8)

式中：

(9)

(10)

(11)

(12)

(13)

2.3 产品贮存寿命的评估

产品的性能参数通常具有特定的分布规律，考虑到数据处理需要，采用目前广泛应用的正态分布来研究产品的性能参数分布规律。

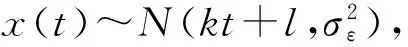
(14)

式中：u1-R为标准正态分布的(1-R)分位数。

对比式(1)和式(14)，可得

x0=kts+l+u1-Rσε

(15)

由式(15)可以求解ts。

但实际应用过程中，k,l,σε都是未知的母体参数，只能用样本的相应参数来代替。然而这种代替是有误差的，对代替误差进行分析之后，根据数理统计理论，可得到x(t)的单侧置信下限为

(16)

即可得到下式：

(17)

式中：t1-R为自由度f=n-2的t分布函数的(1-R)分位数。

对比式(1)和式(17)，可得

(18)

根据上式，用迭代法、插值法或其他数值计算方法求得ts，即为产品的贮存寿命。

3 某密封剂贮存寿命评估

某密封剂具有优异的耐热、耐寒和电性能，现场使用中理化和工艺性能与相应的进口材料接近，使用效果良好，不足之处在于规定的贮存寿命较短，仅为12个月，给物资采购、库房存放、现场使用等环节带来诸多不便。为更合理地确定其贮存寿命，对其开展了自然贮存试验。邵氏A硬度反映胶料的硫化程度，是灌封料现场使用时重要的质量控制指标，该密封剂的指标要求为邵氏A硬度≥35。试验过程中，按ASTM D2240标准方法，利用Zwick-A型邵氏硬度计在出厂t=0，t=12月和t=15月时测试样品的邵氏A硬度，得到试验数据如表1所示。

表1 密封剂自然贮存试验硬度数据

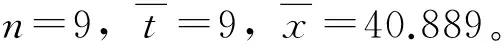
当x0=35时，由x0=at0+b求得t0=52.615。

选取两个比t0小的值t1，t2；R(t)取0.99，即t1-R取-2.998，按式(18)计算x1，x2。

t1=18时，求得x1=35.547。

t2=21时，求得x2=34.891。

根据t1，t2，x1，x2，利用插值法，可求得对应于x0=35的ts=20.501，表明产品的贮存期达到20个月时，能够满足规定要求的置信度0.99，即产品对应于0.99可靠度的贮存寿命为20.5个月。

实际使用过程中，该密封剂贮存20个月后，测试得到的硬度数据绝大部分能够满足使用要求，与该方法确定的贮存寿命基本一致，表明该方法具有足够的可信程度。

4 结 论

根据建立的贮存寿命模型和提出的基于自然贮存试验的贮存寿命评估方法，可在较短的时间内得到更加合理可信的贮存寿命信息。对某密封剂进行实例应用得到的结果与实际情况基本一致，表明该方法是合理可行的，具有实践应用价值，可以为确定产品的贮存寿命提供依据和参考。

需要说明的是，提出的方法适用于性能参数单一的产品。推广应用到具有多个性能参数的复杂产品时，应先分析每个参数的重要度，识别出对产品完成任务具有重要影响的参数(一个或若干个)，并利用该方法评估得到该产品对应于每个重要参数的贮存寿命，选取最小值作为产品的贮存寿命。

[1] GJB451A-2005，可靠性维修性保障性术语[S].

[2] 张春华，温熙森，陈循. 加速寿命试验技术综述[J].兵工学报, 2004, 25(4): 485-490.

[3] 耿新民, 张建平, 谢秀中，等. 真空荧光显示屏恒定及步进应力加速寿命试验的研究[J]. 电子器件, 2005, 28(4): 714-718.

[4] 郑波, 葛广平. 基于步进应力加速寿命试验的引信贮存寿命评估[J]. 北京理工大学学报, 2003, 23(5): 545-547.

[5] 邓爱民, 陈循, 张春华，等. 加速退化试验技术综述[J]. 兵工学报, 2007, 28(8): 1002-1007.

[6] 王玉明, 蔡金燕. 基于板级电路加速退化数据的可靠性分析[J]. 电子产品可靠性与环境试验, 2009, 27(1): 9-12.

[7] 李坤兰. 恒温加速退化试验的灰色预测[J]. 装备环境工程, 2011, 8(4): 20-24.

[8] 陈兵, 李星. 加速寿命试验技术在国内外的工程应用研究[J]. 强度与环境, 2010, 37(6): 31-38.

[9] 盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 北京：高等教育出版社，2001：297-303.

Evaluation Method of Storage Life Based on Natural Storage Experiment

Chen Zhifang,Wang Junhua

(China Airborne Missile Academy, Luoyang 471009, China)

In order to gain a rational evaluation upon product’s storage life, the storage period is studied. A mathematic model of the storage life is established, and a method of natural storage experiment is proposed. The evaluation method of the storage life based on data of natural storage experiment is given. The data of natural storage experiment for a certain sealant is applied with this method. The experiment result generally keeps up with actual condition.The rationality and practicality of the method are indicated.

storage life; storage period; mathematic model; natural storage experiment; evaluation

10.19297/j.cnki.41-1228/tj.2016.06.016

2016-05-04

陈智芳(1987-)，男，河南洛阳人，工程师，研究方向是武器装备系统可靠性工程。

TJ760.7

A

1673-5048(2016)06-0080-03