面向LTE的超低复杂度FFT处理单元设计
2016-02-09陈杰男胡剑浩
费 超,卢 浩,陈杰男,胡剑浩
(电子科技大学 通信抗干扰技术国家级重点实验室,四川 成都 611731)
面向LTE的超低复杂度FFT处理单元设计
费 超,卢 浩,陈杰男,胡剑浩
(电子科技大学 通信抗干扰技术国家级重点实验室,四川 成都 611731)
该文提出了一种超低复杂度的、面向长期演进(LTE)上行的快速傅里叶变换(FFT)混合基处理单元的设计与实现。由Cooley-Tukey算法与质因数算法,LTE上行所需FFT可以分解到基2,3,5上。该文基于Winograd傅里叶变换设计了FFT处理单元,利用折叠技术对多模下FFT进行了算法单元复用,利用正则符号数(CSD)乘法结合树形结构与Horner法则优化其中的乘法器结构。相比已有方法,关键路径时间降低16.7,乘法器面积降低78.9,总面积降低62.1。
快速傅里叶变换;长期演进计划;Winograd傅里叶变换;正则有符号数;
长期演进(LTE)上行通信系统[1]需要35种不同长度的离散傅里叶变换(DFT),其长度可以被表达[2]为:

式中,α,β,γ为整数。
由于采用了非基于2的FFT的模式,因此传统基于2点的FFT优化算法不能直接应用到LTE的上行电路中。
在未来的通信中,对硬件复杂度和能耗都提出了很高的要求,特别是在面向绿色通信的系统设计中,减少硬件复杂度是很重要的一个需求。
为减少FFT的计算复杂度与硬件复杂度,Cooley-Tukey(CTA)算法[3]通过数学分解使长度为NP点的FFT计算量大幅降低,同时N为2的电路实现已经被广泛研究过[4-6];当FFT长度可以被质因数分解时,质因数算法(PFA)[7]可以比CTA算法计算量更少。WFTA算法[6]通过对旋转因子矩阵分解进一步降低硬件消耗,文献[9-10]中提出了基于WFTA算法的长度可变,效率提升的电路实现方法。这些设计与算法都试图减少乘法器个数等方式减少硬件消耗。
由此,可以根据CTA与PTA算法,将LTE所需FFT逐步分解到2,3,5点上,然后再由小点数2,3,5的WFTA算法来进行FFT实现。因此可以先分解然后计算,并利用复用技术,将混合基下的多种FFT模式进行计算单元的复用。本文基于WFTA算法设计了基2,3,5复用的FFT电路,针对资源消耗较大的乘法器部分,利用正则有符号数[11]表示方法,结合树形方法与Horner法则[12]进行优化。相比目前FFT处理单元设计,在FPGA上,乘法器的查找表资源消耗(LUTs)降低了84.2,总消耗降低了70.9;在硬件逻辑面积开销上,乘法器面积减少了78.9,总面积消耗减少了62.1,同时处理的关键路径时间减少了16.7。
1 FFT分解与WFTA算法
1.1 FFT长度较大时的分解
N点的离散傅里叶变换(DFT)与旋转因子表达式为:

式中,k∈[0,N-1],其矩阵形式为X=W x。文献[10]给出一种对N=N1N2分解算法:

一维角标(n,k)被映射为(n1,n2)和(k1,k2),将[0,N-1]映射成[0,N1-1]×[0,N2-1]。
N1,N2互质由PFA算法将DFT公式改写为:

这样可以先做N1点的FFT:
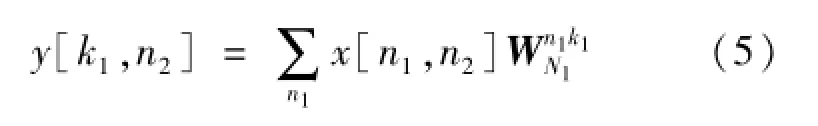
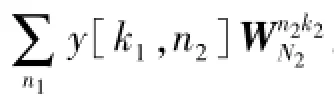
N1,N2不满足互质条件时由CTA算法将DFT原式可改写为:

这样将计算过程转化为先计算N1点的FFT y[k1,n2],经过旋转因子乘法后再进行N2点FFT计算来得到结果。
这样,利用PFA算法和CTA算法可以将LTE中较大的FFT逐步分解,到2点、3点和5点的FFT上。
1.2 较小长度时的WFTA算法实现
当点数较小时,WFTA算法针对FFT的旋转因子矩阵进行分解:

式中,S矩阵和T矩阵的元素只有0和正负1,C矩阵是对角矩阵,只有在与C作计算时候会涉及乘法。文献[8]中给出了具体数学推理过程与分解结果。
2 设计与实现
2.1 电路及复用设计
依据WFTA算法,混合2点、3点和5点硬件分时复用的FFT设计如图1所示。首先设计5点的处理电路,电路中先进行T51到T57预加法,再分别点乘旋转因子,再经过后级加法。然后进行硬件复用,3点时预加法T31与T51复用,T32与T52复用;乘法M32与M52,M33和M53复用;后级加法X32与S52,X33与S54复用。2点FFT时,X21由M51计算得出,同时由M52和S54来计算X22。

图1 2点、3点和5点复用FFT处理单元设计
2.2 基于CSD表示的乘法器优化
考虑乘法器都是常系数乘法器,可以进一步优化从而缩短处理时延和减少硬件开销。
1)正则符号数(CSD)运算
数字的CSD表示中含有的非零位是所有表示法中最少的,利用CSD数表示结合移位相加可以实现常数乘法而且加法数量最少。
由文献[11]的迭代算法将各乘法器系数转换为CSD数,结果如表1所示。C51与C31在二进制上较为简单没有给出,C54系数超过了CSD的表示范围,所以改写成十进制的-1加上CSD表示的-0.538 8。通过CSD表示方式,原本有48个非零位被转换成了27个非零位。按照给出的算法循环可得到各个乘法器系数的CSD表示,如表1所示。
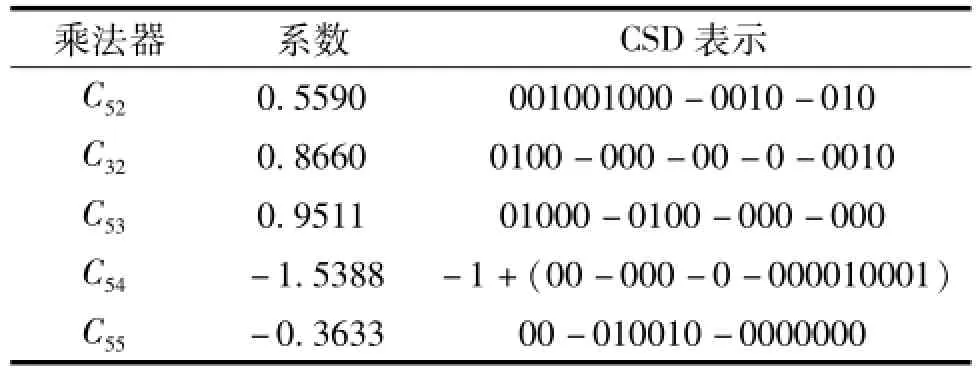
表1 乘法器系数的CSD表示
2)利用Horner法则与减少计算树高
因为采用的计算方式为固定字长,在计算过程中部分和与部分积将被截断,这会带来截断误差。为实现计算精度,速度与硬件开销的相互折中,首先,应该尽量推迟同一括号内的公共缩放运算[12]以减少截断误差。其次,同时计算多个加法时候,将顺序的加法排列成树形结构并尽量降低树高。最后,为避免溢出,可以再额外缩放一位。再经过上述优化,可以得到各个系数的计算方法:
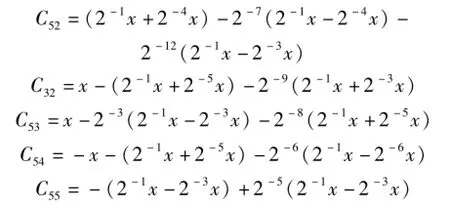
3 算法性能与硬件消耗
3.1 定点化信噪比
FFT的算法仿真定点化信噪比将由下式决定:

式中,Sfloat指浮点信号值,取平方后表示信号功率,Sfix表示定点信号值。frame表示计算的帧数。式[8]是将浮点输出信号的功率求和比上定点化与浮点之间的功率差,然后按功率取对数得出。
对于5点FFT,100 000组随机输入后其定点化信噪比大约为73.514 dB,3点FFT为73.919 dB,2点因为不涉及乘法,信号精度保持不变所以没有给出。
3.2 设计硬件消耗
信号位宽18位,设计环境为XILINX ISE,验证的FPGA为Virtex7,门级电路仿真在Synopsys Design Compiler中进行。最终各器件消耗的查找表(LUTs)、硬件面积消耗和关键路径时间结果如表2和表3所示。

表2 各乘法器资源消耗与关键路径
因电路需要按IQ两路展开处理,表中每个乘法器需要2个,18位选通器共需要8个,18位加法器共需34个。关键路径时间单位为纳秒(ns)。逻辑面积单位为平方微米(μm2)。

表3 加法与选通器资源消耗
由表2与表3的仿真结果可以看出,在FPGA上,处理单元中18 bit乘法器的LUT消耗为576,选通器共占72个LUT资源,加法器消耗的LUT为612。
在消耗的硬件面积上,常数乘法器面积消耗为16 546.22,选通器总面积为1 501.68,加法总面积为19 679.2。同时关键路径的处理时间为7.72 ns。
3.3 硬件消耗比较
如今绝大部分LTE中FFT设计都直接使用18位的实数乘法器资源[4-6],在FPGA中实现时其查找表LUTs资源对比如表4所示,其中Xilinx 18位实数乘法器资源为364LUTs,Altera为367LUTs。

表4 FPGA上资源消耗对比(以LUT计算)
可看出在FPGA上仿真时,LUT资源消耗大幅度减少,乘法器资源开销减少至使用IPCORE的16左右,总资源开销降至原来的30左右。而逻辑面积开销与关键路径时长如表5所示,对比的方法为在Synopsys Design Compiler下直接相乘。

表5 硬件资源对比
由表5可以看出乘法器的关键路径得到减少,从而处理单元的关键路径得到了减少,其次乘法器面积开销缩减了78.9,总面积减少了62.08。
4 结束语
LTE系统中不同的35种长度的FFT可以由算法分解到基2,3,5上,本文首先介绍了LTE上行的FFT分解算法,然后基于WFTA算法利用折叠技术构建了2点、3点和5点分时复用的电路,并针对硬件资源消耗较大的乘法器,利用CSD乘法,依据Horner法则与减少树高的方式进行优化,相比较已有FFT处理单元设计,在FPGA上乘法器资源减少了84.2,总资源开销减少至70.9;在处理单元逻辑面积开销上,乘法器面积缩减了84.2,总面积降低了62.08,同时将处理关键路径缩减了大约16.7。
[1]3GPP LTE.Evolved universal terrestrial radio access(EUTRA);Physical Channels and Modulation[S].2008.
[2]XILINX.Discrete Fourier transform V3.0 product specification[EB/OL].[2008-06-27].http://www. xilinx.com.
[3]COOLEY JW,TUKEY J W.An algorithm for the machine calculation of complex Fourier series[J].Mathematics of Computation,1965,19(90):297-301.
[4]CHEN J,HU J,LI S.High throughput and hardware efficient FFT architecture for LTE application[C]//Wireless Communications and Networking Conference(WCNC),2012:826-831.
[5]CHANG Y N.An efficient VLSI architecture for normal I/O order pipeline FFT design[J].Circuits and Systems II:Express Briefs,2008,55(12):1234-1238.
[6]PENG S Y,SHR K T,CHEN C M,et al.Energy-efficient 128~2048/1536-point FFT processor with resource block mapping for 3GPP-LTE system[C]//International Conference on Green Circuits&Systems.[S.l.]:[s.n.],2010:14-17.
[7]GOOD I J.The interaction algorithm and practical Fourier analysis[J].Journal of the Royal Statistical Society(Series B),1960,20(2):361-372.
[8]SILVERMAN H F.An introduction to programming the Winograd Fourier transform algorithm(WFTA)[J].IEEE Transactions on Acoustics Speech&Signal Processing,1977(25):152-165.
[9]CHEN J,HU J,LEE S,et al.Hardware efficient mixed radix-25/16/9 FFT for LTE systems[J].IEEE Transactions on Very Large Scale Integration(VLSI)Systems,2015,23(2):221-229.
[10]CHEN J,HU J.A variable length FFT module for LTE applications[C]//IEEE International Conference on Communications Technology&Applications.[S.l.]:IEEE press,2009:376-380.
[11]REITWIESNER GW.Binary arithmetic[J].Advances in Computers,1960(1):231-308.
[12]PARHI K K.VLSI digital signal processing systems:Design and implementation[M].New York:John Wiley&Sons Press,1999:372-374.
Low-Complexity Mixed-Radix FFT Design and Implementation for LTE-Oriented
FEI Chao,LU Hao,CHEN Jienan,HU Jianhao
(National Key Laboratory of Science and Technology on Communication,University Of Electronic Science And Technology Of China,Chengdu 611731,China)
In this paper,a low cost mixed-radix FFT processor is proposed based on the uplink of LTE standards.Firstly CTA and PFA are employed to factorize large length FFT to small mixed-radix FFTs.After that,WFTA is utilized to implement the mixed-radix FFTs with reusing technology.Finally,a CSD multiplier with Horner structure is employed to optimize the constant multiplier.Compared with existing methods,the proposed method has78.9hardware saving in multiplier and 62.1in total design,as well as16.7processing time reduction.
fast Fourier transform;long term revolution;WFTA;CSD;
TN929.5
A
10.3969/j.issn.1672-4550.2016.06.011
2015-04-20;修改日期:2016-11-21
国家自然科学基金(61371104)。
费超(1993-),男,硕士,主要从事通信专用集成电路方面的研究。
