一道习题的研究及其应用

□杭 静

一道习题的研究及其应用

□杭 静

有这样一道题：3个球队进行单项循环比赛（参加比赛的每一个球队都与其他所有的球队各赛一场），总的比赛场次是多少？4个球队呢？5个球队呢？n个球队呢？

图1

如何解决这个问题呢？我们先从最简单的情况开始，可以将3个球队用字母A、B、C来表示，设想让他们站在一条直线上，如图1，则参加比赛的每一个队都与其他所有的队各赛一场，相当于数出图形中线段的条数.一般来说，对于一条直线上有多个不重合端点的图形，要数出其中线段的条数，根据线段有两个端点的特征，可以先固定第一个端点，再以其余的点为另一个端点组成线段，然后固定第二个端点，与其余的点（第一个点除外）组成线段，依此类推，直到找出最后的线段为止.按这种顺序识图可以避免遗漏、重复现象.图1中固定A点，有2条线段：AB和AC；固定B点，有1条线段BC，则共有线段2＋1＝3条.类似地，如果是4个球队，可以将4个球队用字母A、B、C、D来表示，设想让他们站在一条直线上，如图2，则参加比赛的每一个队都与其他所有的队各赛一场，相当于数出图形2中线段的条数，仿上可知，图2中共有3＋2＋1＝6条线段，它们分别是线段AB、线段AC、线段AD、线段BC、线段BD、线段CD.用这种方法可以得到如下一般性的结论：

图2

下面，我们一起看看应用这个模型可以解决哪些问题.

例14支排球队进行单循环比赛（参加比赛的每两支球队之间都要进行一场比赛），则总的比赛场数为场.

例2如图3，数一数图中共有多少个长方形？

图3

这个模型也适合于数角等问题.

例3如图4，从点O引m条射线OA、OB、OC、…、OD，则图中有多少个锐角？

图4

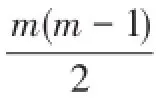
思考题：如果平面上有m（m≥3）个点，其中任意3个点都不在同一条直线上，那么，过两点画一条直线，一共可以画多少条直线？