基于医学影像学的心血管支架力学性能分析

徐 江， 杨 杰， 杨 基， 黄 楠， 刘亚龄

（1．西南交通大学力学与工程学院，四川成都610031；2．西南交通大学材料科学与工程学院，四川成都610031；3．里海大学工程与应用科学学院，宾夕法尼亚州伯利恒18015）

基于医学影像学的心血管支架力学性能分析

徐 江1， 杨 杰1， 杨 基1， 黄 楠2， 刘亚龄3

（1．西南交通大学力学与工程学院，四川成都610031；2．西南交通大学材料科学与工程学院，四川成都610031；3．里海大学工程与应用科学学院，宾夕法尼亚州伯利恒18015）

为了寻找更为简便的基于医学影像学狭窄血管建模的方法，利用特征轮廓提取的简化建模方法，建立了基于狭窄冠脉CT图像的血管支架-狭窄血管耦合有限元模型，对比分析了血管支架在基于CT的狭窄血管模型和理想化狭窄血管模型中的力学行为，引用临床研究结果分析了两种模型计算的合理性．研究结果表明，两种模型在支架的应力分布、撑开刚度、回弹率、“狗骨头”率、血管管腔面积等力学性质上均存在差异，基于CT模型中，血管平均应力1．22 MPa，最小管腔面积6．1 mm2；理想化模型中血管平均应力1．54 MPa，最小管腔面积5．1 mm2；基于CT的有限元模型分析结果更接近临床研究结果．

医学图像；冠脉狭窄；支架；有限元分析

血管支架术以其创伤小、治疗效果好等优势已经在临床上广泛应用，成为治疗心血管狭窄疾病的首选治疗方案［1］．心血管支架植入人体后的力学行为影响血管支架术短期和长期的治疗效果［2-3］，因此分析血管支架植入人体后的力学行为具有重要意义．

早期血管支架力学性能的研究是针对血管支架自身性能，如支架支撑性能、回弹特性、“狗骨头”现象、疲劳性能等，但未揭示血管支架植入人体后的力学性能［4-7］．随之，很多研究提出了不同类型的血管支架、球囊、冠状动脉耦合模型［8-12］，但这些研究均将病变的冠状动脉做了均匀对称理想化处理，忽略了复杂的病变细节，诸如病变斑块的不均匀性、血管的弯曲和扭曲等细节．为了更真实的研究血管支架植入病变血管后的力学性能，文献［13-16］中提出了基于CT（computed tomography）或MRI（magnetic resonance imaging）的医学影像学耦合计算模型．目前，基于医学影像学的血管建模过程复杂，难以满足面向临床的力学分析需要，同时，关于基于医学影像学模型与理想化模型分析结果的对比研究较少．

本文对某病患右冠状动脉狭窄病变普通的CT图像，提出了一种简化建模方法，建立了支架、球囊、真实病变血管耦合的有限元计算模型．同时，根据该病变特征，采用理想化简化建模方法，建立了支架、球囊、血管耦合的有限元模型，对比分析支架植入不同血管模型中力学性质的差异，并将临床研究结果与分析结果进行了对比分析．

1 材料与模型

1．1 基于医学影像的冠状动脉模型

采用的CT图像来自某男性患者，62岁，有长期抽烟史，经诊断其狭窄病变位于右冠状动脉RCA2段，狭窄长度（12±0．5）mm，狭窄程度为Ⅱ级，斑块类型疑为轻度钙化斑块．图像数据由64位螺旋CT扫描得到，包含273张CT图像序列，图像分辨率512×512像素，像素大小为0．33 mm×0．33 mm，见图1（a）～（c），图中红色标记区域为冠脉轮廓．将CT扫描影像利用Mimmics软件（比利时Materialise公司）三维重建，重建过程中采用两次插值函数光滑，调整CT图像层间相关系数为0．95，光滑后的三维几何体见图1（d）和（e）．

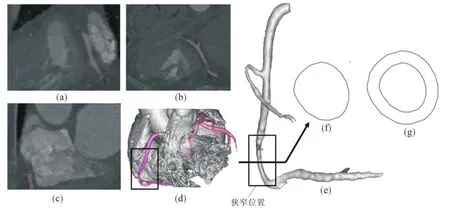
图1 狭窄冠脉CT重建模型Fig．1 CT reconstruction model of coronary artery stenosis

在三维重建的几何模型上依次提取病变段血管的截面，截面间隔1 mm，共计31张，总长度为30 mm．将提取的血管截面用样条曲线拟合，进一步光滑，处理后便于生成连续光滑的几何体和高质量的计算网格，提取和光滑的血管内壁轮廓见图1（f）．根据文献［13-14］对血管外壁进行处理，假设血管外壁为与健康血管外壁相同，血管壁厚平均约为0．9 mm，平均管腔内直径为3．2 mm．文中将上述提取的病变血管内壁轮廓，按照健康冠脉平均厚度向其外法线外拓得到血管壁．经此过程处理得到血管截面形状见图1（g）．

将经样条曲线光滑后30张截面顺序导入Abaqus／CAE中，按照截面中心坐标进行定位重新生成三维几何体，然后划分有限元网格．定位生成的几何体和划分的有限元网格见图2．

图2（b）、（c）均为病变血管有限元网格，网格全部采用八节点六面体缩减积分单元（C3D8R），共计划分单元68 040个．

CT重建的模型为病变血管内壁，根据文献［14］，血管壁冠脉壁厚分为3层：内膜0．28 mm，中膜0．32mm，外膜0．30 mm．斑块分布在血管内膜内部，区域划分参考文献［16］对病变血管结构解剖的结果，狭窄斑块在轴向与环向呈不均匀分布．

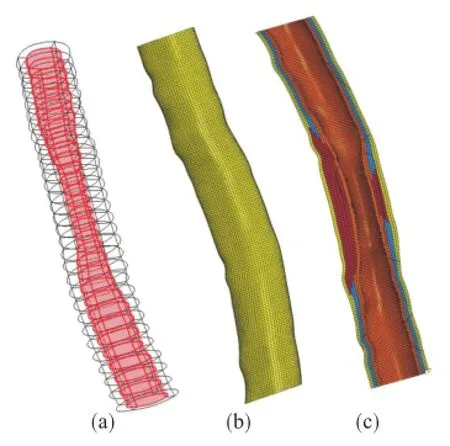
图2 基于CT狭窄血管几何模型与有限元网格Fig．2 The geometry model and FE meshes of the CT-based vascular stenosis

血管和斑块材料性质均为超弹性材料，其能量密度函数为

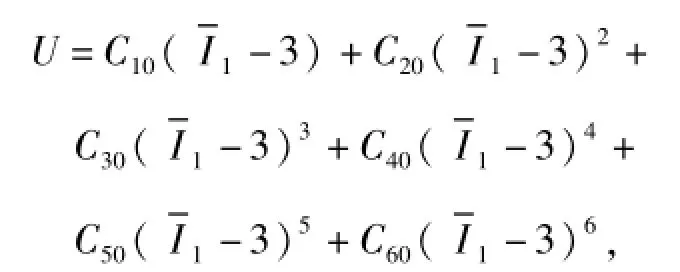
C10、C20、C30、C40、C50、C60均为材料系数，可根据文献［17］的实验数据确定．

基于CT冠脉模型有限元网格细节与材料分布见图3．

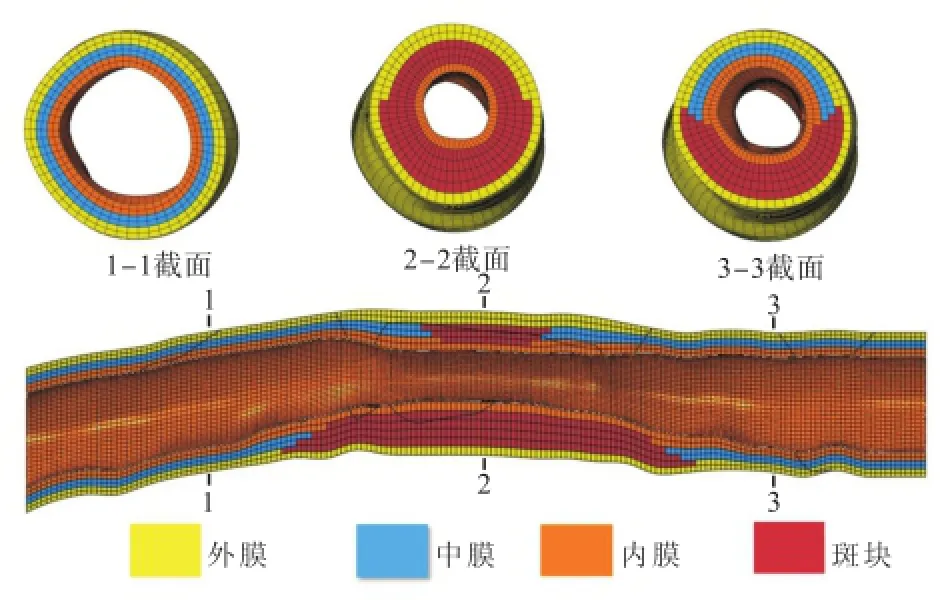
图3 基于CT冠脉模型有限元网格细节与材料分布Fig．3 FE meshes and material distribution of the CT-based coronary artery model

1．2 简化的血管模型

简化的血管模型处理方法与文献［8-12］的建模方法相同，血管被简化为等直圆柱体，管腔直径3．2mm，长度30mm，壁厚0．9mm，分为3层：内膜0．28 mm，中膜0．32 mm，外膜0．30 mm．狭窄斑块长度10 mm，狭窄处血管直径1．7 mm，狭窄两端做过渡处理．血管各层与斑块材料属性与基于CT建模的血管模型材料属性相同，具体见表1．

表1 各部分能量密度函数系数Tab．1 Coefficients of strain energy density function for each layer MPa

模型网格全部采用八节点六面体缩减积分单元（C3D8R），共划分79 616个单元．模型材料分布于网格划分见图4．

1．3 支架模型

支架采用类Cypher支架，长14．00 mm，内直径1．45 mm，厚度0．10 mm．

支架材料为316 L不锈钢，各向同性理想弹塑性材料，弹性模量210 GPa，泊松比0．3，屈服应力280 MPa，密度7 800 kg／m3，材料信息见文献［8］．

模型网格全部划分为八节点六面体缩减积分单元（C3D8R），共计52 221个，模型见图5．

1．4 球囊模型

球囊采用两端封口的模型，球囊撑开后直径3．50 mm，厚度0．15 mm，材料为各向同性线性材料，弹性模量900 MPa，泊松比0．3，密度1 500 kg／m3，材料信息见文献［13］．有限元网格划分为四节点四边形缩减积分膜单元（M3D4R），共计划分为12 120个．

1．5 边界条件与设置

在支架撑开与卸载分析前，预先完成了支架压缩与输运到病变位置．

支架撑开与卸载过程中，支架左右两端环向位移约束，左端轴向位移约束，径向位移设置为自由；球囊左右两端全约束，内表面施加均匀压力0．80 MPa；冠脉两端自由度全约束．

支架与球囊、球囊与冠脉、支架自身和球囊自身均设置接触，接触采用罚函数算法．各个接触对中的摩擦因数均设为0．2．

考虑支架撑开过程的高度非线性，模拟采用准静态模拟方法（Abaqus／Explicit模块）完成．为保证模拟结果的准确性，需控制计算中动能所占比例为势能的5%以下［18］，计算中通过增长加载时间满足这一要求，加载撑开时间8 s，卸载时间5 s．

图4 简化的狭窄血管模型网格与材料分布Fig．4 Meshes and material distribution of the simplified vascular stenosis model

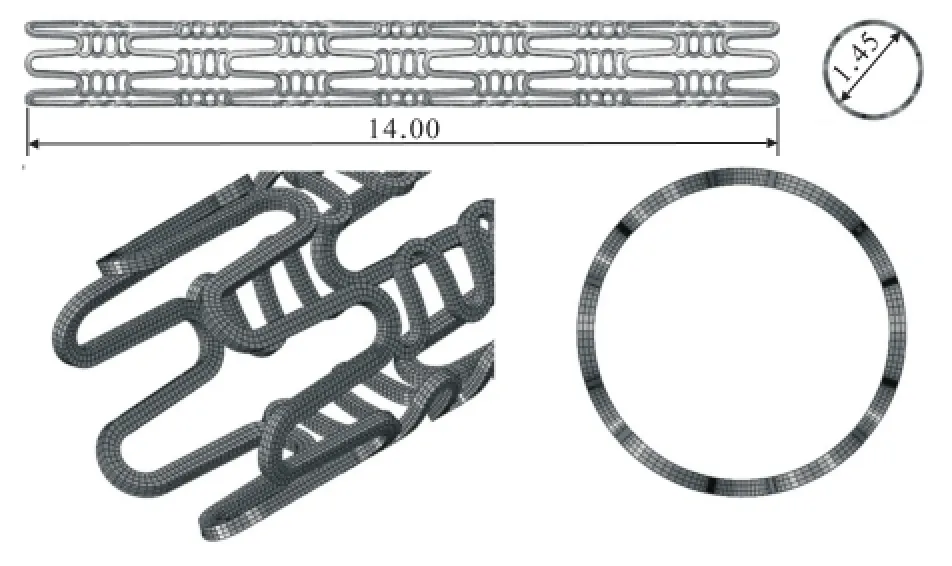
图5 支架模型与有限元网格Fig．5 The stent model and its FE meshes

2 计算结果与讨论

图6为血管撑开过程动能与势能随时间的变化，与势能相比，动能始终保持较低水平，由此判断计算过程是合理的．图7为支架在病变冠脉中撑开过程．基于CT模型，由于考虑了病变冠脉的弯曲和截面为非理想圆形，支架处于偏心位置，而理想化模型中支架与血管轴线重合．当压力P＝ 0．45 MPa时，支架均被非均匀撑开，左右两端出现“狗骨头”现象，基于CT模型中支架两端“狗骨头”出现的程度不一致，如图7（a）所示，而理想化模型中左右两端“狗骨头”现象相同；当P＝0．80 MPa时，支架与球囊完全打开，如图7（b）所示，基于CT模型冠脉被撑开的程度是上侧大于下侧冠脉，理想化模型中血管被均匀撑开，这与病变斑块在冠脉环向不均匀分布相关．

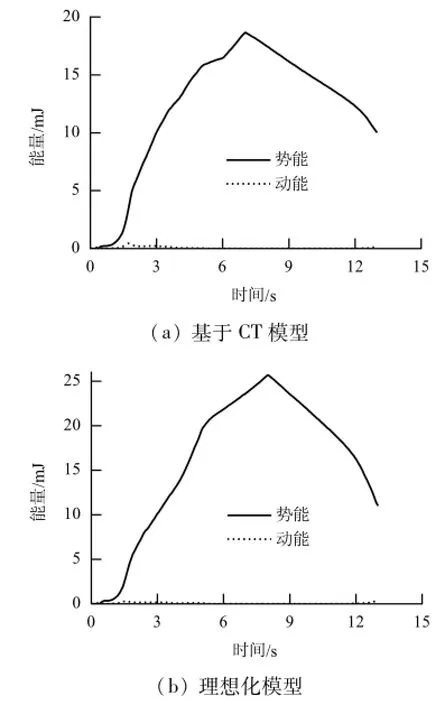
图6 动能和势能随时间的变化Fig．6 Variation of internal energy and kinetic energy with time

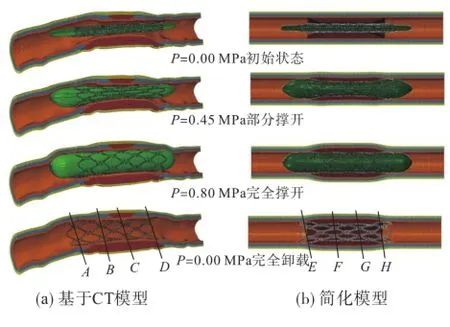
图7 支架在狭窄血管中撑开过程Fig．7 The process of stent deployment in the coronary artery with stenosis

为了进一步研究由于冠脉的不均匀性导致的支架性质在不同位置的差异，文中取了4个典型位置进一步研究支架撑开直径随压力变化规律．两个模型中分别取4个典型位置，如图7中A、B、C、D和E、F、G、H所示．图8为模型中4个不同位置支架直径-压力曲线．在基于CT模型中，不同位置支架的力学性质完全不同，但理想化模型中支架的力学性质仅在中间与端部表现出差异．从卸载规律上看，基于CT模型中支架两端表现出相同的卸载规律，图8中表现为A、D曲线在卸载阶段重合，支架回弹量很小；中间位置（B、C位置）卸载规律类似，但与支架两端不同，中间位置支架回弹量较大，C位置回弹量大于B位置；在理想化模型中两端回弹规律相同，中间位置回弹规律也相同．

支架在两端与中间位置力学性能差异与血管的狭窄程度和斑块的分布形式相关．血管中间位置狭窄，血管的约束在支架中间位置大于两端，故在撑开刚度上中间位置大于两端；卸载时，支架中间位置的回弹量大于支架两端．对于基于CT模型同处于支架中间的B、C位置上，B位置的斑块分布小于C位置，故而B、C位置支架力学性质存在差异；而理想化模型中狭窄位置斑块分布相同，所以F、G位置支架力学性质基本相同．

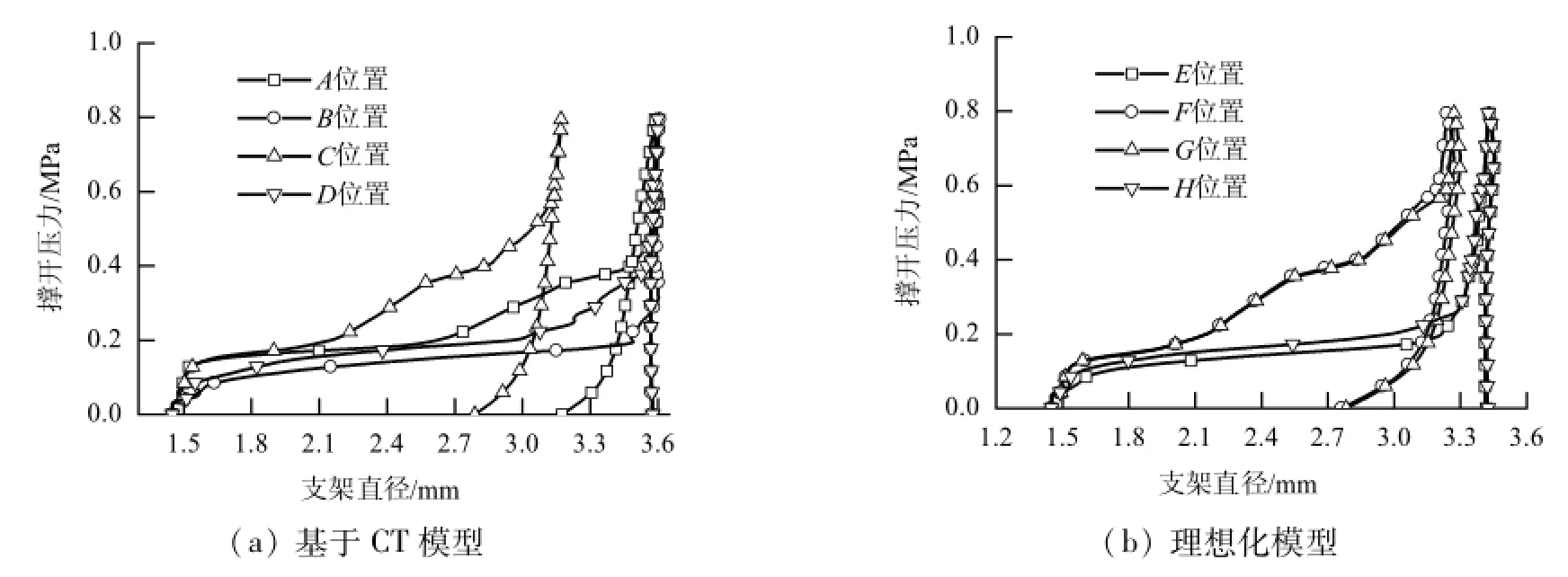
图8 支架撑开过程压力-直径的关系Fig．8 Pressure-diameter relationship of the stent during the deployment process

图9为血管支架植入后冠状动脉内膜上应力分布．由图9可知，基于CT模型，撑开初期，当P＝0．45 MPa时，血管内皮最大应力1．42 MPa，最大区域出现在两端，且左端分布区域大于右端；当完全撑开后，内膜最大应力达到了1．96 MPa，分布在血管狭窄处，呈环向不均匀分布，血管下侧应力大于上侧；当完全卸载后，内膜上最大应力为0．726 MPa，最大应力区域均匀分布在血管中间部分，呈不规则斑点状分布．

对于理想化模型在撑开初期，内皮最大应力1．59 MPa，集中在斑块两端；当完全撑开，最大应力为2．22 MPa，位于斑块边缘位置，出现明显的支架状压痕，环向均匀分布；当完全卸载后，最大应力为0．88 MPa，主要分布在斑块边缘且呈规则分布．

从应力水平上看，理想化模型中支架植入后血管应力水平高于基于CT模型中．从应力分布看，对于基于CT模型，血管与斑块并非对称均匀结构，血管下侧对支架的作用力大于上侧，故支架对血管内膜损伤程度是下侧大于上侧．而对于理想化模型，斑块在环向上呈对称分布，血管对支架的约束为均匀，故应力在血管上分布也呈均匀分布．

图10为血管支架植入人体后管腔面积变化［19］，图中：前端为1＃、2＃截面；末端为8＃、9＃截面．通过对植入人体的142根支架在手术结束时和手术后6个月用血管内超声（IVUS）检查得到统计结果．结果表明，支架植入后在支架中间位置血管的管腔面积最小，越远离中间位置管腔面积最大，且呈线性分布；术后6个月，血管发生再狭窄，管腔面积中间位置最小，两端最大，中间位置发生再狭窄的程度大于其他位置．

本文统计了类似支架植入血管后不同位置血管管腔面积，如图11所示．基于CT模型，支架植入后中间位置平均管腔面积最小，两边依次增大，越远离中间位置平均管腔面积越大；对于理想化模型，斑块区域管腔面积最小处基本相同，管腔面积最大处在支架边缘位置，而并非距中间位置最远处．从管腔平均面积看，基于CT模型最大管腔面积9．7 mm2，最小管腔面积6．1 mm2；理想化模型最大管腔面积8．9 mm2，最小管腔面积5．1 mm2．与文献［19］对比，基于CT模型得到的管腔面积从分布形式和大小更接近临床研究结果．

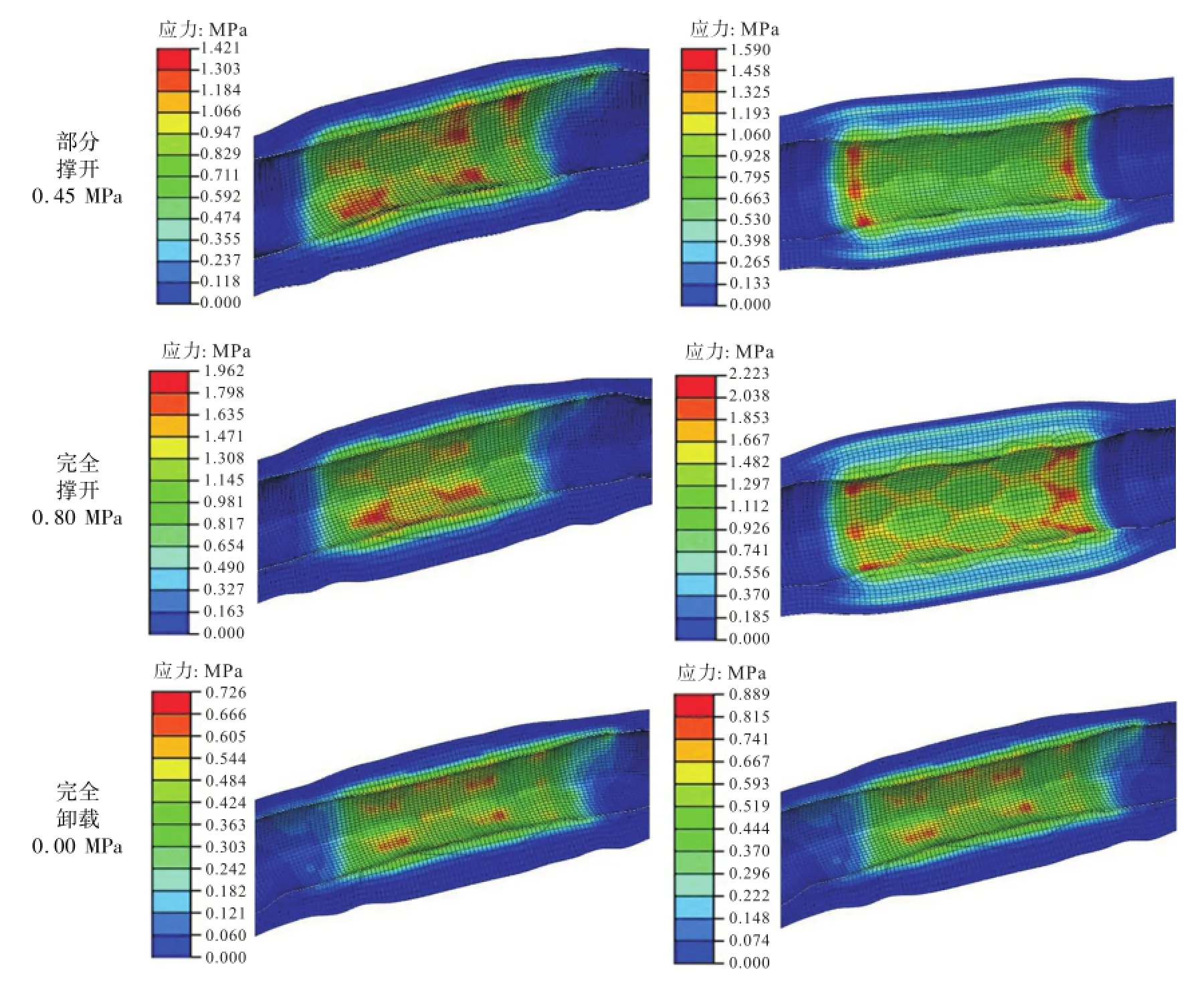
图9 血管支架植入后冠状动脉内膜上应力分布Fig．9 Von Mises stresses distribution in the intima of the artery after stent implantation

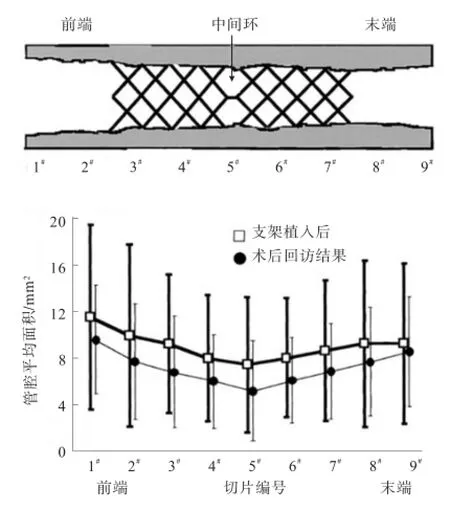
图10 血管支架植入人体后管腔面积变化［19］Fig．10 Luminal area changes after stent implantation into human body［19］

由图9知，基于CT模型，最大应力分布均出现在斑块中间位置，表明血管支架植入对血管损伤大于其他位置；而对于理想化模型，最大应力主要分布在斑块两端，这是由于支架植入对血管损伤两端大于中间．损伤程度越大越容易引发再狭窄，基于CT模型的结果更能与文献［19］研究结果吻合．

需要指出，图9仅为支架植入某一时刻血管上应力分布，不能表征整个植入过程血管应力水平．

定义支架植入过程中血管平均应力为

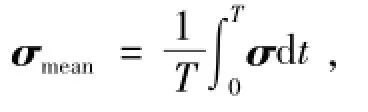
式中：T为支架撑开经历的时间；

σ为每一时刻血管的应力张量．

图12为两种不同模型中支架植入过程血管平均应力分布．由图12可知，基于CT模型血管应力主要分布在斑块中间位置，环向成不均匀分布；理想化模型应力主要分布在斑块边缘处，环向成均匀分布．从应力分布看，基于CT模型的结果更接近文献［19］的研究结果．

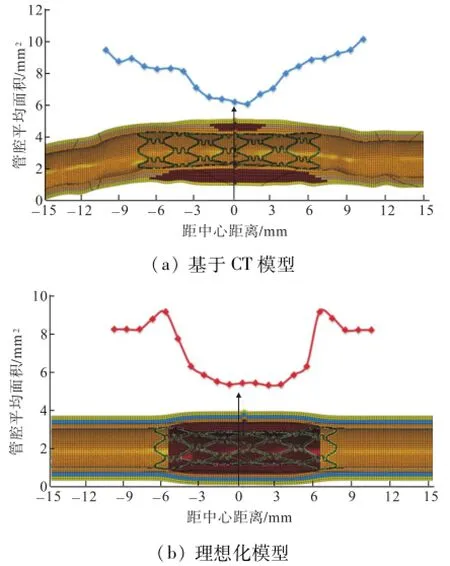
图11 支架植入后血管管腔面积变化Fig．11 Luminal area changes after stent implantation

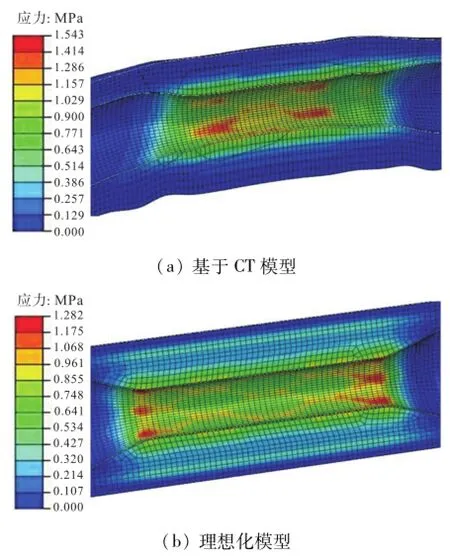
图12 支架植入过程血管平均应力Fig．12 Vascular mean stress in the stent implantation process

临床上常用血管内超声（IVUS）检测血管支架植入后的状态，如管腔面积、支架均匀性、贴壁性等重要指标．类似地，图13为支架植入过程血管截面处应力分布，类似IVUS图，两模型中截面位置相同．

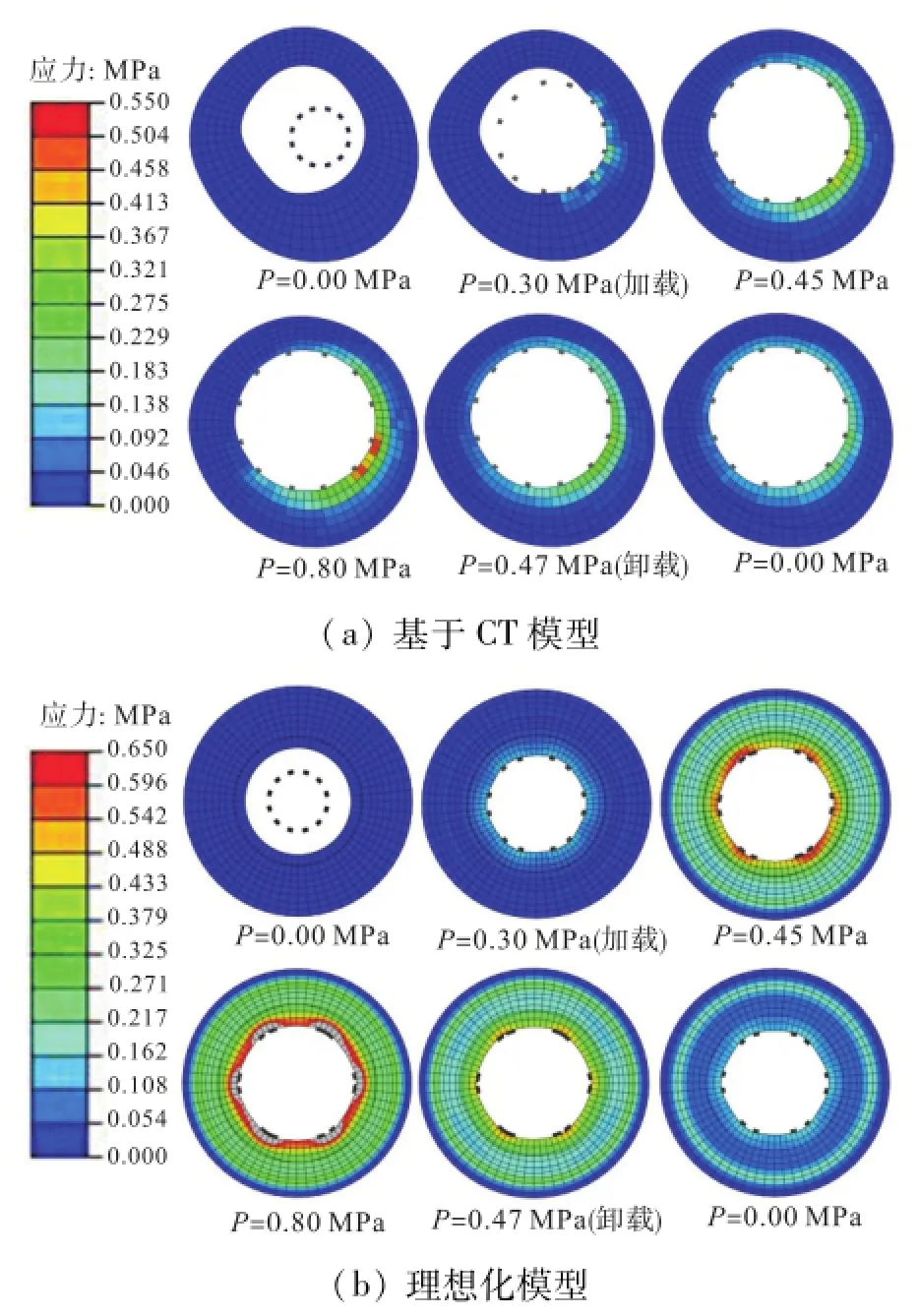
图13 支架植入过程血管截面处应力分布Fig．13 Stress distributions in a vascular section during the deployment process

由图13可知，基于CT模型，初始状态支架不在截面中心位置，撑开过程中支架对血管造成的应力呈不均匀分布，卸载后血管应力在环向仍呈不均匀分布；而理想化模型，初始状态支架位于截面中心位置，撑开过程和卸载后血管上应力呈均匀分布．这是由于基于CT模型截面和斑块分布不均匀而理想化模型中截面和斑块呈均匀对称分布造成的．支架植入人体后血管应力分布表征了支架对血管的损伤程度，基于CT模型应力在环向的不均匀分布表明术后由于支架植入损伤造成血管内膜增生在环向呈不均匀生长，理想化模型意味着术后内膜增生环向呈均匀分布．

3 结束语

本文分别在基于狭窄冠脉CT图像建立冠脉模型和简化的冠脉模型中分析了血管支架植入冠脉的过程，并对比分析了血管支架撑开直径与压力关系、支架植入后血管应力分布规律等重要力学性质，引用了临床上关于支架再狭窄的研究结果，分析不同冠脉模型计算的合理性．结果发现：基于CT

模型由于考虑病变血管几何性质和材料属性的不均匀性等细节，支架和血管的力学性质呈不均匀分布，理想化模型中支架和血管的力学性质多呈均匀性分布；基于CT的冠脉模型的分析结果更接近临床研究结果，利用医学影像学建模分析支架植入人体内力学性质较简化分析模型更为合理．

致谢：西南交通大学博士创新基金资助．

［1］ GARG S，SERRYS P W．Coronary stents current status［J］．Journal of the American College of Cardiology，2010，56（1）：1-41．

［2］ KUTRYK M J B，ONG A T L．Drug therapy：coronaryartery stents［J］．The New England Journal of Medicine，2006，354（1）：483-495．

［3］ SANGIORGI G，MELZI G，AGODTONI P，et al．Engineering aspects of stents design and their translation into clinical practice［J］．Annali Dellistituto Superiore Di Sanita，2007，43（1）：89-100．

［4］ ETAVE F，FINET G，BOIVIN M，et al．Mechanical properties of coronary stents determined by using finite element analysis［J］．Journal of Biomechanics，2001，34（1）：1065-1075．

［5］ 李建军，罗七一，谢志勇，等．冠脉支架的疲劳寿命的有限元分析［J］．医用生物力学，2010，25（1）：68-73．LI Jianjun，LUO Qiyi，XIE Zhiyong，et al．Fatigue life analysis of coronary stent by finite element analysis［J］．Journal of Medical Biomachanics，2010，25（1）：68-73．

［6］ 李红霞，张艺浩，王希诚．基于有限元模拟的支架扩张、血流动力学及支架疲劳分析［J］．医用生物力学，2012，27（2）：178-185．LI Hongxia，ZHANG Yihao，WANG Xicheng．Analysis of stent expansion，blood flow and fatigue life based on finite element method［J］．Journal of Medical Biomechanics，2012，27（2）：178-185．

［7］ 杨杰，黄楠，杜全兴．血管支架随机失稳扩展均匀性问题的模型和应用［J］．力学学报，2008，40（1）：79-85．YANG Jie，HUANG Nan，DU Quanxing．Model and applicaiton of uniformity expansion in randomized structure of intravascular stent［J］．Chinese Journal of Theoretical and Applied Mechanics，2008，40（1）：79-85．

［8］ GERVASO F，CAPELLIC，PETRINI L，et al．On the effects of different strategies in modeling balloonexpandable stenting by means of finite element method［J］．Journal of Biomechanics，2008，41（1）：1206-1212．

［9］ BEULE M D，MORTIER P，CARLIER S G，et al．Realistic finite element-based stent design：the impact of balloon folding［J］．Journal of Biomechanics，2008，41（1）：383-389．

［10］ YANG Jie，HUANG Nan，DU Quanxing．A nonuniform expansion mechanical safety model of the stent［J］．Journal of Medical Engineering＆Technology，2009，33（1）：525-531．

［11］ LALLY C，DOLAN F，PRENDERGAST P J．Cardiovascular stent design and vessel stress：a finite element analysis［J］．Journal of Biomechanics，2005，38（1）：1574-1581．

［12］ MORTIER P，HOLZAPFELG A，BEULEM，et al．A novel simulation strategy for stent insertion and deployment in curved coronary bifurcation：comparison of three drug-eluting stents［J］．Annals of Biomedical Engineering，2010，38（1）：88-99．

［13］ ZAHEDMANESH H，JOHN K D，LALLY C．Simulation of a balloon expandable stent in a realistic coronary artery-determination of the optimum modelling strategy［J］．Journal of Biomechanics，2010，43（11）：2126-2132．

［14］ KIOUSISD E，GASSER T C，HOLZAPFEL G A．A numerical model to study the interaction of vascular stents with human atherosclerotic lesions［J］．Annals of Biomedical Engineering，2007，35（11）：1857-1869．

［15］ KIOUSIS D E，GASSER T C，HOLZAPFEL G A．Smooth contact strategies with emphasis on the modeling of balloon angioplasty with stenting［J］．Int．J．Numer．Meth．Engng，2008，75（1）：826-855．

［16］ CHAN A H，CHAN R C，SHISHKOV M，et al．Mechanical analysis of atherosclerotic plaques based on optical coherence tomography［J］．Annals of Biomedical Engineering，2004，32（11）：1494-1503．

［17］ GASSER T C，OGDEN R W，HOLZAPFEL G A．Hyperelastic modeling of arterial layers with distributed collagen fiber orientations［J］．Journal of the Royal Society Interface，2006，3（1）：15-35．

［18］ GASTALDI D，MORLACCHI S，NICHETTI R，et al．Modelling of the provisional side-branch stenting approach for the treatment of atherosclerotic coronary bifurcations：effects of stent positioning［J］．Journal of Biomechanics and Modeling in Mechanobiology，2010，9（5）：551-561．

［19］ HOFFMANN R，SMINTZ G，DUSSAILLANT G R，et al．Patterns and mechanisms of in-stent restenosis：a serial intravascular ultrasound study［J］．Circulation，1996，94（1）：1247-1254．

（中文编辑：秦 瑜 英文编辑：兰俊思）

Mechanical Properties Analysis of Coronary Stent Based on Medical Images

XU Jiang1， YANG Jie1， YANG Ji1， HUANG Nan2， LIU Yaling3
（1．School of Mechanics and Engineering，Southwest Jiaotong University，Chengdu 610031，China；2．School of Material Engineering and Science，Southwest Jiaotong University，Chengdu 610031，China；3．College of Engineering and Applied Science，Lehigh University，Bethlehem 18015，USA）

In order to find a simple method to build the coronary artery stenosis model based on medical images，a simplified narrow coronary artery-stent coupling finite element（FE）model based on CT images was built using the feature contour extraction method．The mechanical properties of the stent in an ideal coronary artery stenosis was then studied using the CT-based FE model in comparison with the ideal simplified artery FE model．In addition，some clinical study results were used to verify the rationality of the two models．The results show that some differences in mechanical properties existed between the two models，such as the stress distribution，expansion stiffness，recoil rate，“dog bone”rate，and the mean area of blood vessel．For the CT-based model，the mean stress of vessel was 1．22 MPa and the minimal area of vessel after stent implantation was 6．1 mm2，while they were 1．54 MPa and 5．1 mm2，respectively，in the ideal simplified model．The results obtained by the CT-based simplified model was more close to the clinical results than the ideal simplified model．

medical images；coronary stenosis；stent；finite element analysis

TB121；R318．01

A

0258-2724（2016）01-0201-08

10．3969／j．issn．0258-2724．2016．01．028

2013-03-01

国家自然科学基金资助项目（10872176）

徐江（1987—），男，博士研究生，研究方向为生物力学、工程力学，E-mail：xujiang0123＠163．com

杨杰（1970—），男，教授，博士，博士生导师，研究方向为生物力学、工程力学，E-mail：yangchenjie＠swjtu．cn

徐江，杨杰，杨基，等．基于医学影像学的心血管支架力学性能分析［J］．西南交通大学学报，2016，51（1）：201-208．