计及覆冰和空气阻尼的弓网动态受流特性

段甫川， 刘志刚， 宋 洋， 张 静

（西南交通大学电气工程学院，四川成都610031）

计及覆冰和空气阻尼的弓网动态受流特性

段甫川， 刘志刚， 宋 洋， 张 静

（西南交通大学电气工程学院，四川成都610031）

为研究覆冰和环境风对弓网受流的影响，基于模态分析法，在充分考虑覆冰对接触网系统质量和刚度影响的基础下，重新推导了覆冰接触网运动微分方程，并引入静风载荷引起的空气阻尼对其进行修正．结合受电弓归算质量模型进行动态仿真计算，研究了不同覆冰厚度、风速、风攻角对弓网接触压力的影响．研究结果表明：无风时覆冰厚度的增加会造成弓网接触性能的变差；在静风环境下，由于线索覆冰改变了接触线阻尼，来流风向是静风载荷影响弓网接触性能的主要因素，来流风向越接近水平，对弓网受流性能的影响越小．

弓网动态受流；覆冰；静风载荷；空气阻尼；风攻角

当前，在世界范围内电气化铁路正得到广泛应用，特别是近十年来我国电气化铁路得到迅速发展．弓网系统是电气化铁路的重要组成部分，主要负责将电能输送至电力机车，是一种露天、无备用的电气设备，因而会受到冰雪、大风等外部环境因素的影响，降低安全性和可靠性．随着近年来接触网覆冰事故的不断发生，覆冰及环境风给电气化铁路造成的危害逐渐引起人们的重视．目前国内外关于覆冰及风载荷对输电线路的危害的研究已逐渐成熟，如Den Hartog等于1932年开展了关于覆冰导线风致振动稳定问题判别准则的研究［1］；Nigol O等利用有限元分析对覆冰输电线路的均匀风流场条件下的驰振初始条件和运动规律进行了研究［2］；张勇等通过进行覆冰特高压输电塔线偶联体系的风洞试验，验证了覆冰导线自身动力特性变化规律［3］；顾明等研究了扇形和准椭圆形两种形状覆冰导线的气动特性［4］；李黎等对输电塔-线体系的舞动和风振控制进行了研究［5］．随着近年来高速铁路的不断发展，对于弓网动态行为的研究也日趋成熟，如梅桂明等采用受电弓与刚性悬挂接触网的耦合动力学模型对弓网恒接触压力进行了分析［6］；文献［7］研究了承力索张力对弓网受流质量的影响；文献［8］分析了高速列车通过隧道时其弓网动力学变化特征；文献［9］通过建立高速受电弓-接触网的有限元耦合模型，对弓网系统的受流性能进行了验证分析．

在输电导线风振理论及弓网动力学的研究基础上，文献［10］通过对高速铁路接触线气动参数进行仿真，并对其风振响应进行分析；文献［11］分析了不同风速下接触网的微风振动现象；文献［12］对高速铁路接触线静态气动力参数进行了仿真计算，并通过风洞试验进行验证；文献［13］研究了水平风作用下接触线的振动响应；文献［14］通过实测风功谱反演了作用在接触网上的脉动风载荷，对不同风速和风攻角对弓网受流的影响进行了研究，在此基础上，文献［15-16］采用接触网线索的几何非线性，对现有模型进行修正，研究了接触网几何非线性对风偏计算的影响．

然而有关覆冰对弓网动力学行为影响的研究却鲜有报道，仅文献［17］通过对不同覆冰厚度的接触线进行绕流仿真，建立了高速铁路接触网有限元模型，研究了覆冰对接触线气动参数和风振响应的影响；文献［18］利用ANSYS建立不同覆冰厚度的接触网静态响应模型，研究了覆冰厚度对承力索和接触线驰度及下锚处位移的影响．目前，尚未有学者对覆冰和环境风载荷同时作用下弓网受流特性的变化进行研究．接触网线索覆冰不仅会引起系统质量和刚度的改变，同时还会引起接触网线索气动特性的改变，对气动力的作用造成影响．本文以接触网运动微分方程为基础，同时考虑线索覆冰引起的系统重力变化和静风载荷引起的空气阻尼对弓网动力学方程进行修正，分析覆冰、静风载荷耦合作用对弓网接触性能的影响．

1 接触网覆冰的起因及覆冰载荷分析

1．1 接触网覆冰的起因及类型

气候是造成接触网覆冰的主要原因，在雨夹雪或冻雨天气，且空气湿度较大有风条件下，极易出现覆冰．引起接触网覆冰的因素主要包括［19］过冷却水滴大小、风速风向、空气湿度和空气温度，在此条件下形成的覆冰种类主要包括5种：晶状雾凇、粒状雾凇、湿雪、雨凇和混合淞，其中以雨凇危害最为严重，多由冻雨造成，呈透明玻璃体，同接触线表面具有较强附着力，且不易脱落．受到接触网结构的影响，工作状态下承力索和接触线均承受恒定张力，同时中恒通过多根吊弦进行连接，因此通常不会出现扭转，其覆冰形状主要为扁平状，如图1所示［18］．

图1 覆冰接触网Fig．1 Iced catenary

1．2 覆冰载荷模型建立

1．2．1 新月形接触线／承力索覆冰载荷模型

考虑承力索和接触线覆冰形状为新月形，其截面图见图2，其中θice为自然凝冰角（设雨量和风速均在较低水平，取30°），d为承力索直径，b为覆冰厚度．

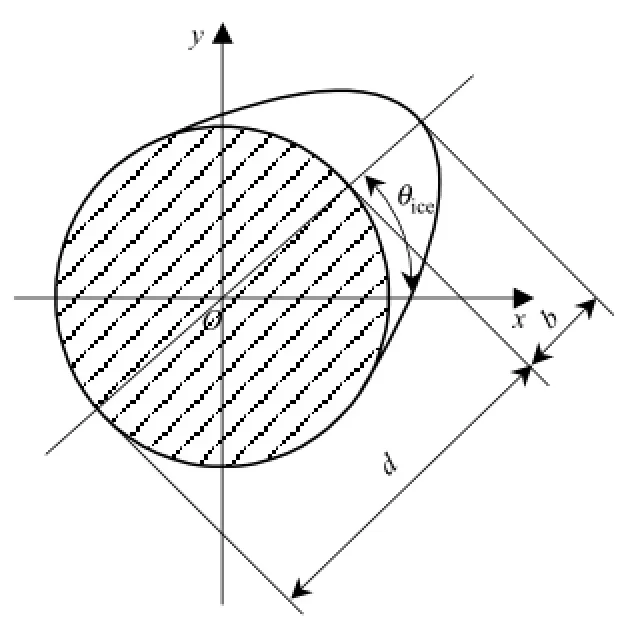
图2 新月形覆冰承力索／接触线截面图Fig．2 Cross-section of crescent-shaped iced messenger wire／contact wire

根据文献［20］，可采用式（1）对承力索上的新月形覆冰质量进行计算：

式中：ρice为覆冰密度，kg／m3；mA为覆冰承力索单位长度质量，由此可得新月形覆冰承力索线密度：

式中：ρa为无覆冰状态下承力索线密度；ρA为新月形覆冰承力索的线密度．

由于接触线和受电弓会发生相对滑动，导致接触线覆冰厚度减小，因此在计算时将接触线覆冰厚度取为同时刻承力索覆冰厚度的50%，则可得到同时刻新月形覆冰接触线的线密度：

式中：ρb为无覆冰状态下的接触线线密度；ρB为新月形覆冰接触线线密度．

1．2．2 扇形接触线／承力索覆冰载荷模型

考虑承力索和接触线覆冰形状为扇形，其截面图见图3，其中θice的取值同1．2．1节．

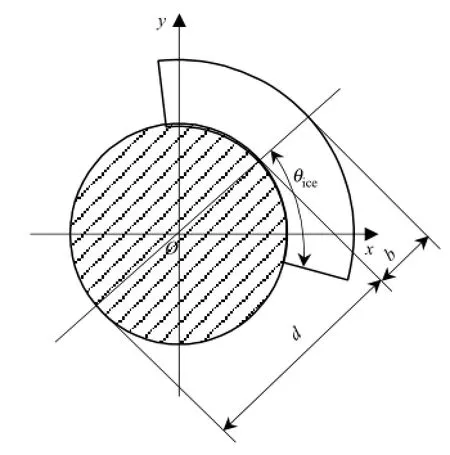
图3 扇形覆冰承力索／接触线截面图Fig．3 Cross-section of fan-shaped iced messenger wire／contact wire

此时，单位长度承力索扇形覆冰质量为

则扇形覆冰承力索线密度为

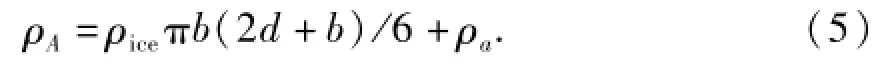
由于接触线和受电弓会发生相对滑动，导致接触线覆冰厚度减小，在计算时将接触线覆冰厚度可取为同时刻的承力索覆冰厚度的50%［8］，则可得到同时刻覆冰接触线的线密度：

1．2．3 D形覆冰接触线／承力索载荷模型建立

当覆冰类型变为D形覆冰时，如图4所示，由于D形覆冰形状的不规则，目前尚无较为准确的公式可对覆冰后承力索／接触线的线密度进行直接计算，对其计算需要结合现场实际的覆冰形态，我们今后将对这一问题进行研究．

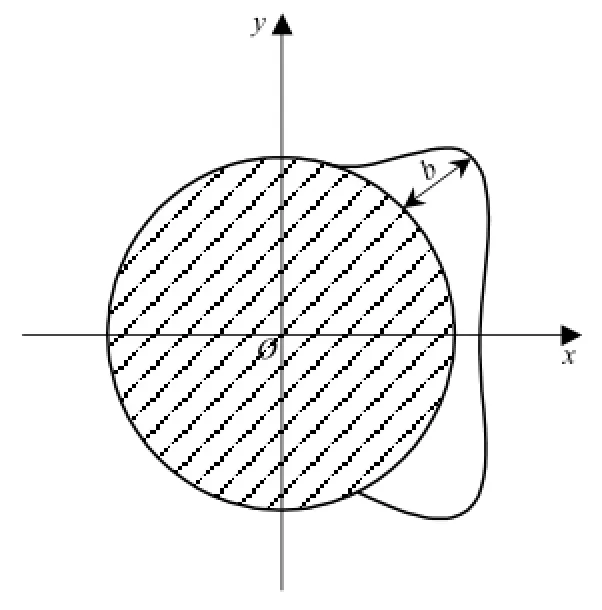
图4 D形覆冰承力索／接触线截面图Fig．4 Cross-section of D-shaped iced messenger wire／contact wire

2 覆冰弓网系统运动微分方程

2．1 覆冰接触网运动微分方程

由于接触线和承力索具有相似的力学性能，因此取长度为d x的覆冰承力索单元体，对其进行受力情况分析，如图5所示．

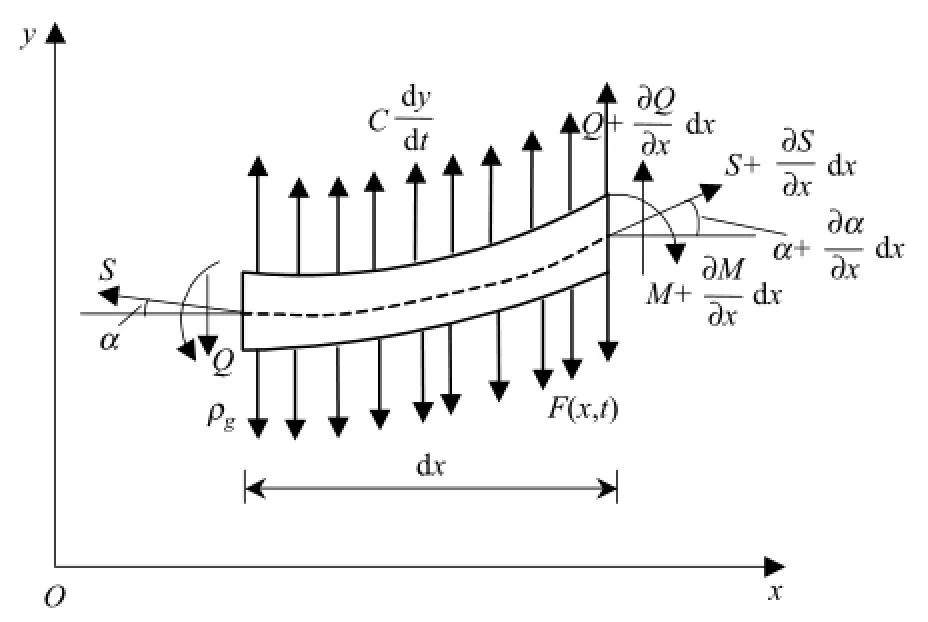
图5 单位长度覆冰承力索受力结构Fig．5 Stress diagram of iced messenger wire unit

图5 中，F（x，t）为单位覆冰承力索除重力外的垂向载荷集度，Q为覆冰承力索单元剪力，M为覆冰承力索单元弯矩，S为覆冰承力索拉力，C为覆冰承力索阻尼，ρg为重力，ρ为覆冰承力索单元的线质量．

对于图5所示的覆冰承力索单元弹性体，将承力索视作欧拉伯努利梁，在竖直方向应用牛顿第二定律，可得如下方程：

式中：

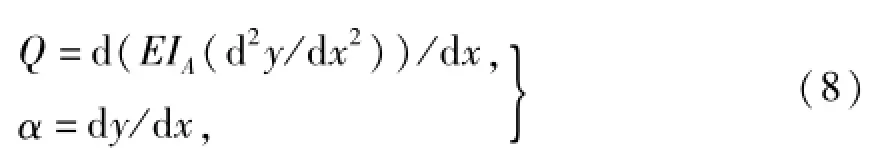
式中：EIA为覆冰承力索抗弯刚度．将式（8）代入式（7）可得：

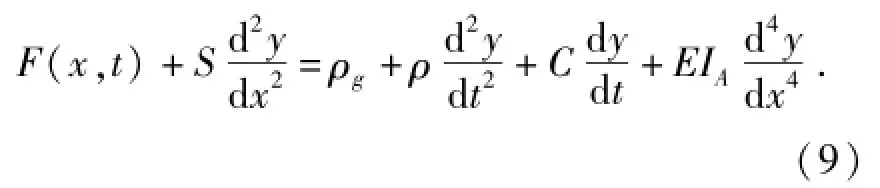
根据文献［21］，将定位器视为阻尼器件，受电弓、支撑杆、吊弦仅在位置xr处对承力索或接触线提供集中力，采用变量分解法对式（9）进行求解，可得到覆冰承力索单元的运动微分方程：

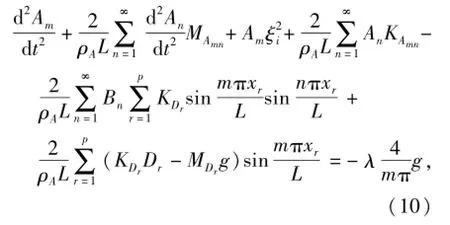
式中：Am、An为承力索广义位移；MAmn为支撑杆、吊弦等对承力索的贡献质量；KAmn为支撑杆、吊弦等对承力索的贡献刚度；Bn为接触线广义位移；Dr、mDr、KDr分别为吊弦静伸长、质量和刚度．λ和ξAi由下式决定：

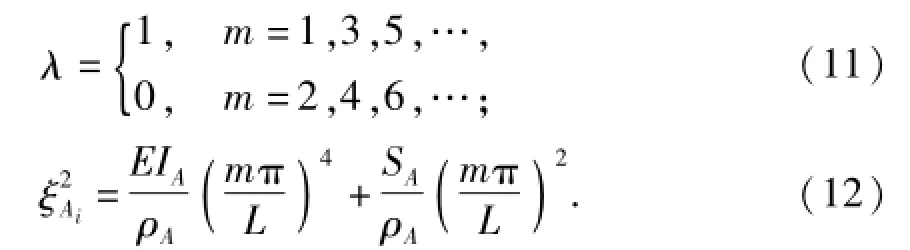
同理，将Am、An替换为接触线的广义位移Bm、Bn，即可得到覆冰接触线的运动微分方程：

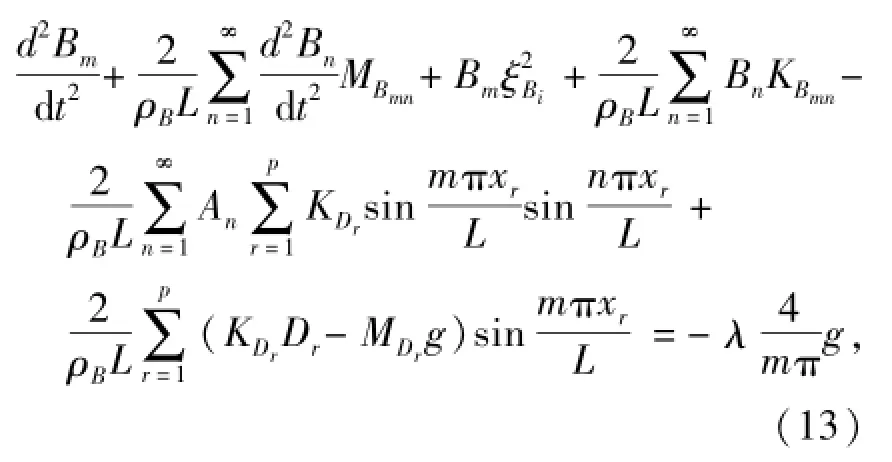
式中：MBmn为定位器、吊弦等对接触线的贡献质量；

KBmn为吊弦等对接触线的贡献刚度．

2．2 受电弓运动微分方程

选取三元受电弓模型，如图6所示，其中：M1、M2、M3分别表示受电弓的弓头、上框架、下框架的归算质量，y1、y2、y3分别表示受电弓的弓头、上框架、下框架的位移量，K1、K2、K3分别表示弓头与上框架、上框架与下框架、下框架与地面之恒的等效刚度，C1、C2、C3分别表示弓头与上框架、上框架与下框架、下框架与地面之恒的等效阻尼，F0为受电弓的抬升力．

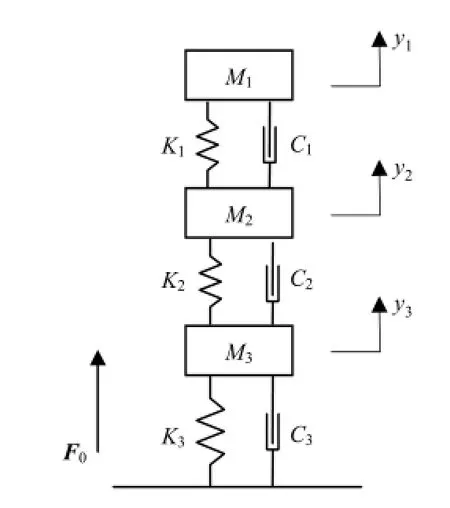
图6 三元受电弓受力模型Fig．6 Three-lumped-mass pantograph model

在竖直方向应用牛顿第二定律，可得受电弓上框架的运动微分方程为

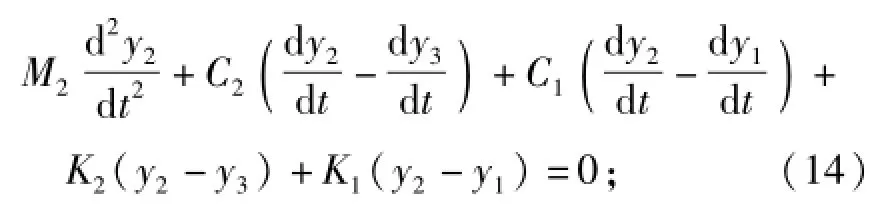
下框架的运动微分方程为

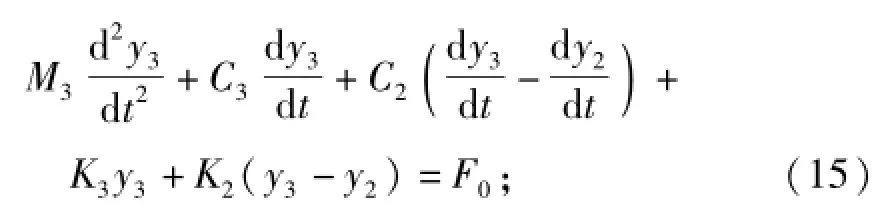
受电弓弓头的运动微分方程为

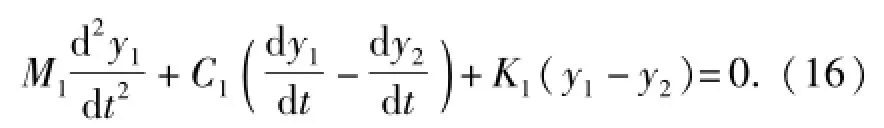
2．3 覆冰弓网系统运动微分方程

采用罚函数耦合受电弓和接触网运动方程［22］，即引入接触刚度Ks，实现弓头与接触网的耦合，因此，将受电弓弓头的运动微分方程修正为

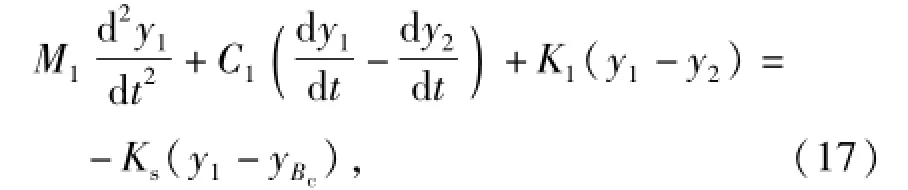
式中：yBc为受电弓在xc处时的接触线位移量，可表示为

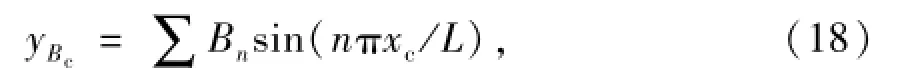
式中：Bn为接触线的第n阶模态广义位移．

联立式（10～18），即可得到覆冰弓网系统的运动微分方程，其矩阵形式可表示为动力学基本方程：

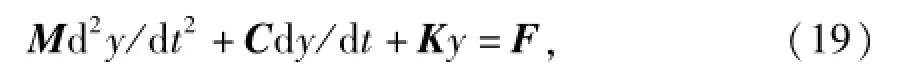
式中：M、C、K、F分别为广义质量矩阵、阻尼矩阵、刚度矩阵、力矩阵．

3 覆冰对弓网接触压力的影响分析

本文选取京津城际弓网系统为研究对象，接触网参数见表1，受电弓选取DSA380作为研究对象，参数见表2．

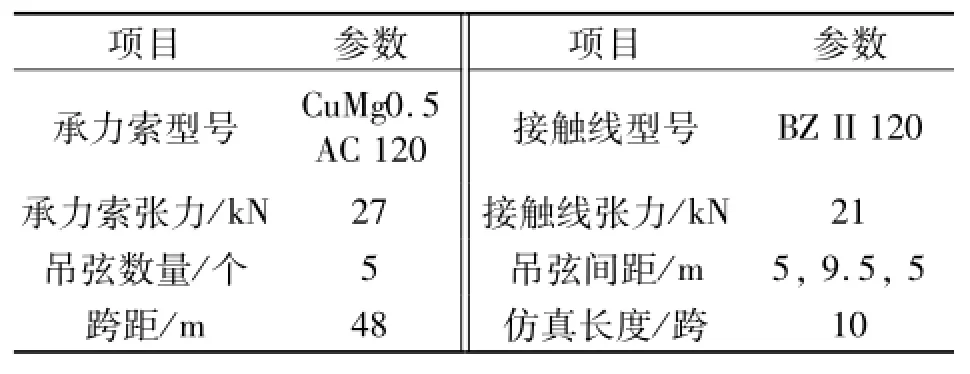
表1 京津城际高速铁路接触网参数Tab．1 Catenary parameters of Beijing-Tianjin high-speed railway

本文选取对接触网危害最大的雨凇型为覆冰类型，厚度选取为10 mm，覆冰密度为890 kg／m3，仿真车速设定为350 km／h，利用Newmark-β算法对覆冰弓网系统的接触压力进行仿真求解，研究不同覆冰厚度对弓网接触压力的影响．

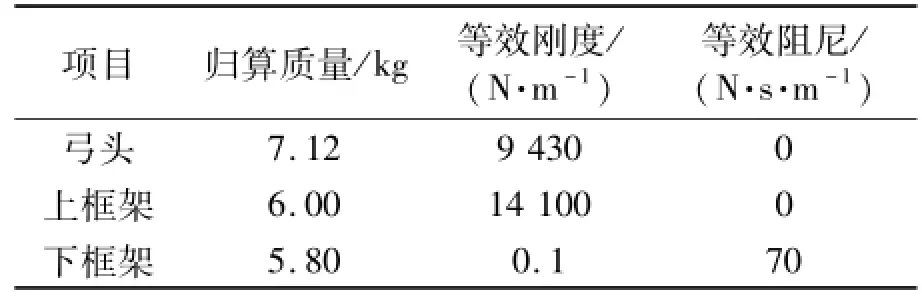
表2 DSA380受电弓参数Tab．2 Parameters of DSA380 pantograph

图7为0、5、10、15 mm覆冰厚度下的弓网接触压力图，表3为其统计数据．

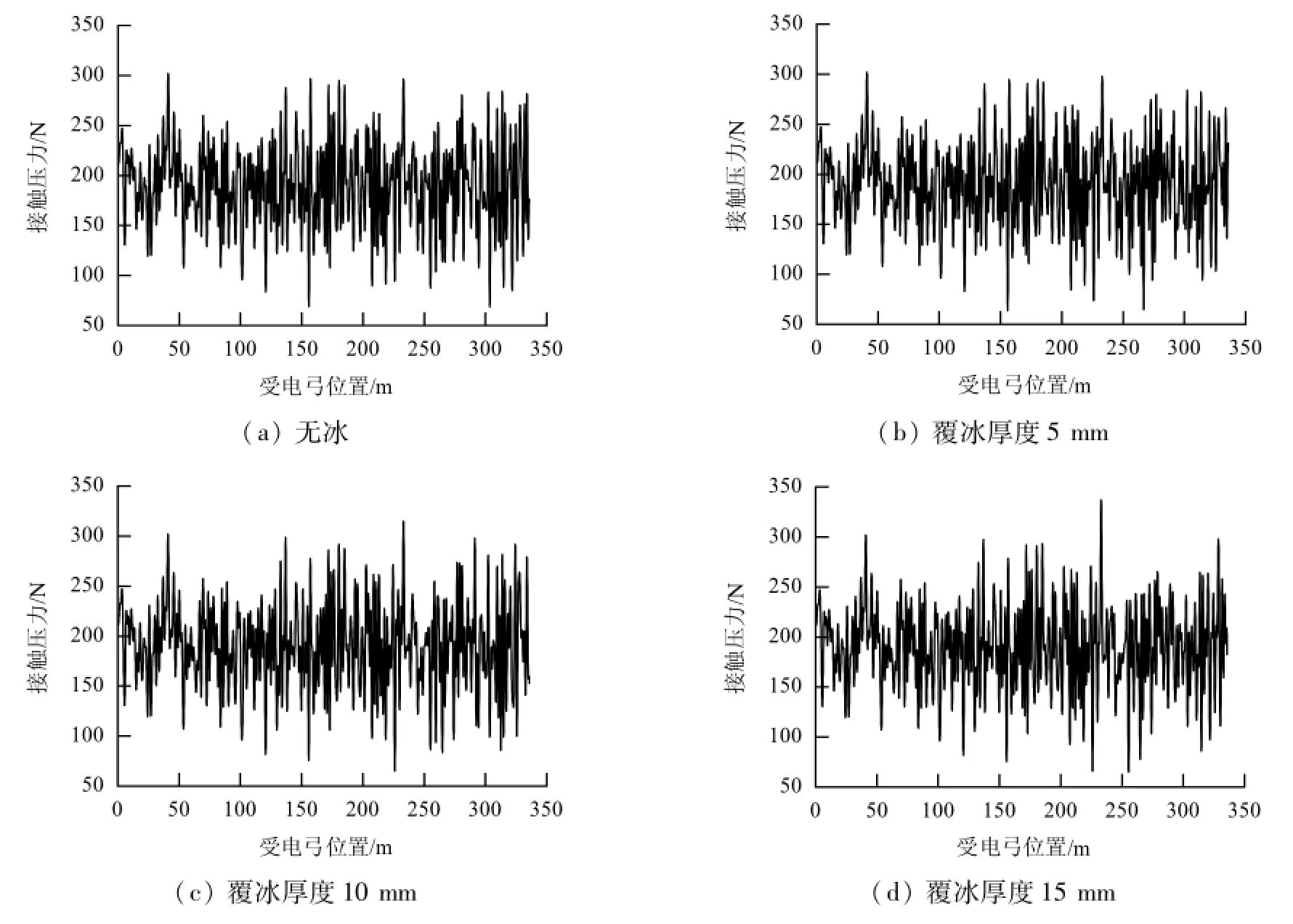
图7 覆冰厚度对覆冰弓网系统接触压力的影响Fig．7 Influence of icing-thickness on the contact force of iced pantograph-catenary

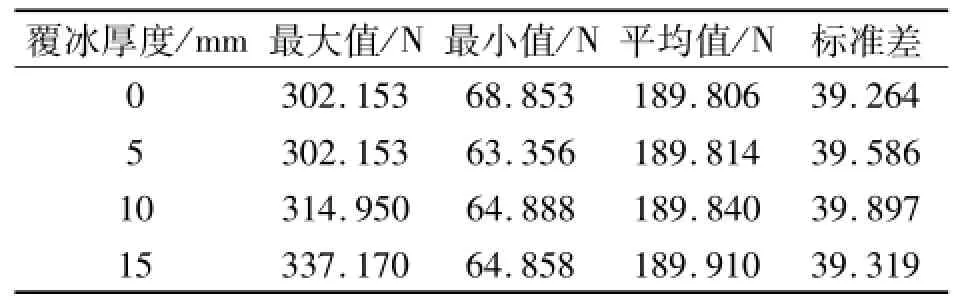
表3 不同覆冰厚度下弓网接触压力变化Tab．3 Contact force with different icing-thicknesses

由图7和表3可知，在无风条件下，当接触线／承力索覆冰在5 mm及以下时，接触压力的统计值并未出现明显变化，此时覆冰并不会对弓网受流特性造成明显影响．但当覆冰厚度达到10 mm及以上时，弓网接触压力统计值的波动变化也不显著，统计数据中的方差并未出现明显变化，但此时接触压力峰值同覆冰厚度5 mm和无覆冰时相比明显增大，特别是在覆冰厚度达到10 mm时，接触压力最大值已达到337．17 N，易造成接触线疲劳损伤，使接触线和弓头过度磨损，引发弓网事故．

4 计及空气阻尼的覆冰弓网接触压力变化

覆冰除会造成接触网线索质量的改变外，还会造成线索横截面积的改变，从而影响承力索及接触线的气动特性．本节将推导覆冰条件下接触线、承力索上的气动阻尼，研究不同风速和风攻角下的气动阻尼对弓网系统动态受流特性的影响．

在静风载荷作用下，承力索／接触线主要受到定常气动力作用，由于其出现上下微幅振动造成攻角出现微小变化，进而产生空气阻尼．图8所示为接触线的迎风受力截面示意图，其中空气以速度Uα、攻角α匀速流过，取接触线的最大计算直径为B，空气密度ρair．在如图所示的风轴坐标系下，FD为阻力，FL为升力，其计算公式分别为

式中，CDα、CLα分别表示在攻角为α时，L-D风轴坐标系下的阻力系数、升力系数．

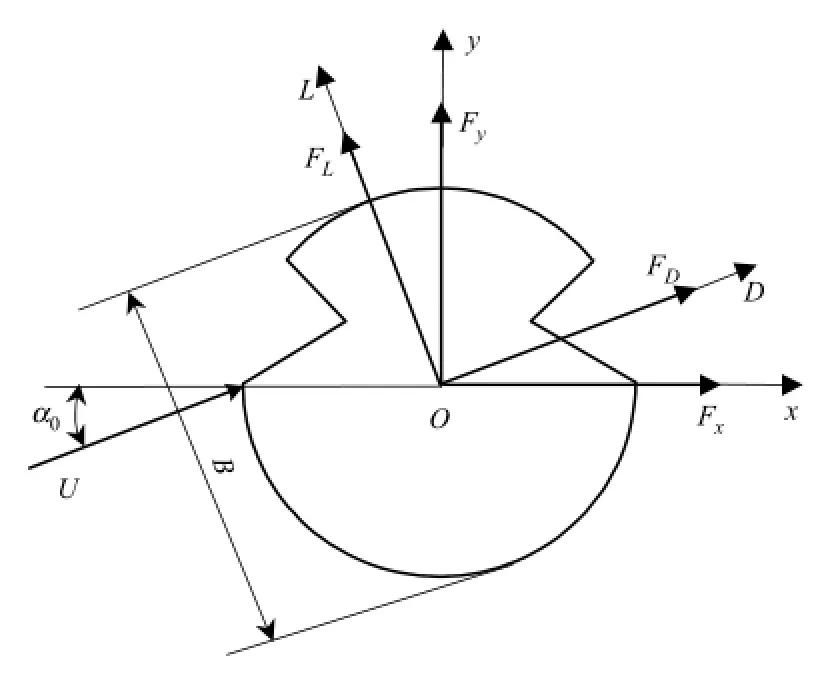
图8 接触线截面迎风受力示意图Fig．8 Force diagram of the iced contact wire section under wind load

接触线受到的垂直方向作用力为

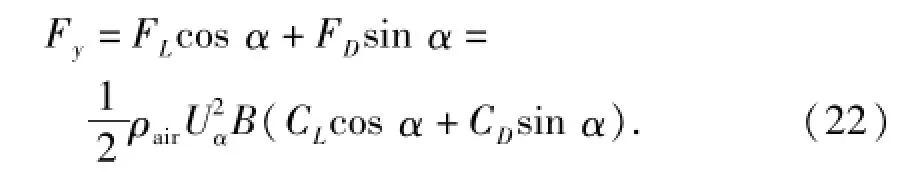
设来流风攻角为α0，将式（22）在α＝α0处进行泰勒展开，可得：

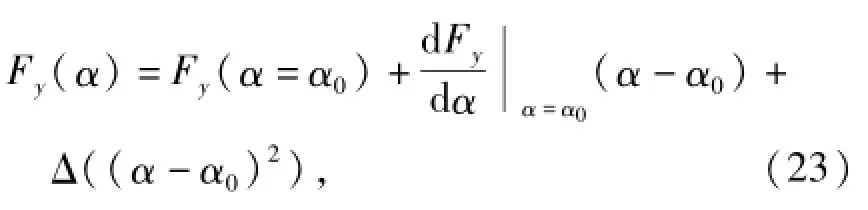
式中：Fy（α＝α0）为定常气动力，与时恒无关，进行动态响应分析时可将其忽略；Δ（（α－α0）2）表示与（α－α0）2有关的高阶项，可忽略．

注意若将接触线竖直方向的单位时恒微位移量表示为˙y，来流风Uα的水平方向风速分量表示为Uxα，则来流速度和攻角可分别表示为

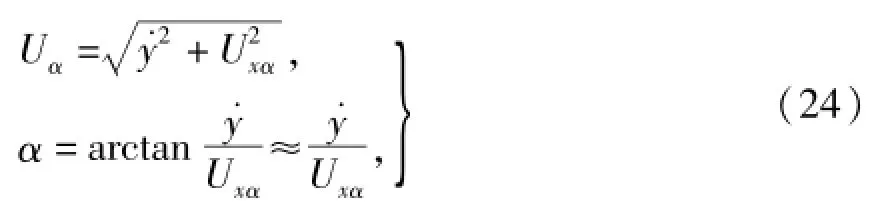
则动态响应分析时，Fy（α）在α＝α0处的动态响应分析一阶泰勒展开式可表示为

因此可将静风载荷下，接触线上的空气阻尼表示为

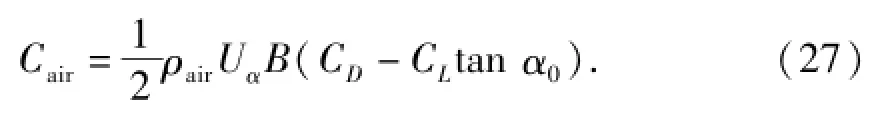
作用在承力索上的空气阻尼推导过程与之相同．其中，CD和CL分别为为攻角α0、风速Uα0时的阻力系数和升力系数，由Fluent仿真得到［10］，具体计算方法如文献［12］中所示，计算结果在西南交通大学单回流串联双试验段工业风洞（XNJD-1）第二试验段中得到试验验证．

4．1 计及空气阻尼接触网运动微分方程修正

2．1节推导了无风环境下覆冰接触网的运动微分方程，当考虑环境风的影响时，静风载荷对于覆冰接触网的影响主要表现为覆冰承力索／接触线竖直方向受力情况的变化，如图9所示．

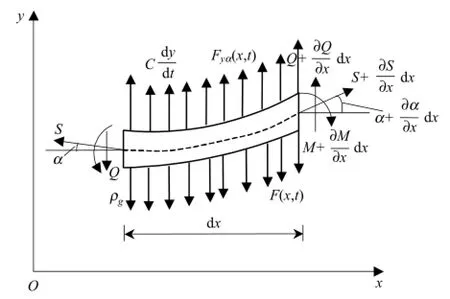
图9 静风载荷下覆冰承力索／接触线单元受力示意图Fig．9 Stress diagram of the iced messenger wire／contact wire under static wind load

图9中，Fyα（x，t）为t时刻在静风载荷Uα的作用下，x位置处承力索单元受到的垂直方向上的静风载荷作用力，因此可将承力索单元的运动微分方程修正为

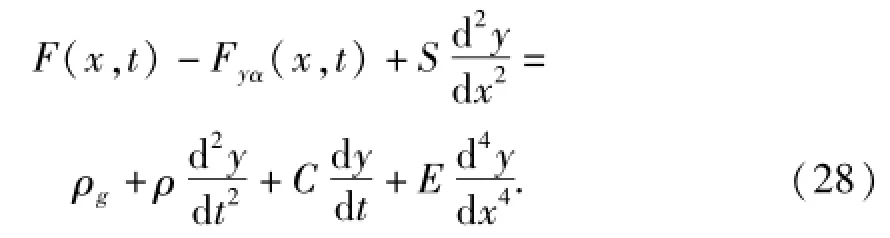
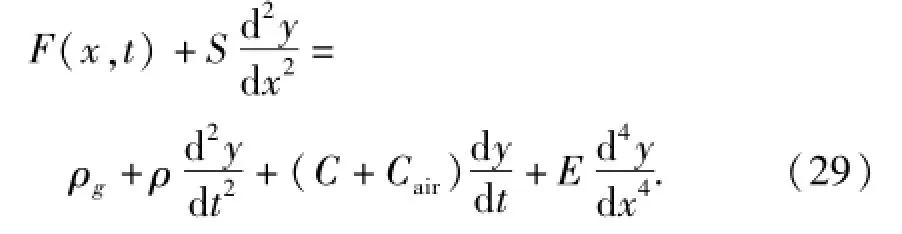
由式（29）可知，静风载荷主要改变了承力索单元的阻尼系数，在如式（19）所示的弓网耦合动力学方程的矩阵形式中，在考虑空气阻尼后，原有系统的阻尼矩阵C发生变化，其对角线元素改变，承力索和接触线所对应的对角线元素分别改变为（CA＋Cair，A）／（2L）、（CB＋Cair，B）／（2L），其中CA、CB分别为承力索、接触线阻尼系数．

4．2 横风作用下覆冰弓网系统接触压力分析

本节研究在横风作用下（即当α＝0时），静风载荷对于弓网接触压力的影响．由于接触线／承力索的空气阻尼作用，平均风可能会引起接触网出现较大振动，影响弓网受流，因此研究覆冰情况下弓网接触压力变化具有一定的价值．根据上文的推导结果，引入不同风速下的接触线／承力索空气阻尼，进行仿真求解，可得到当覆冰厚度为10 mm时，5、10、15 m／s下不同速度的横风对覆冰弓网接触压力的影响，如图10和表4所示．

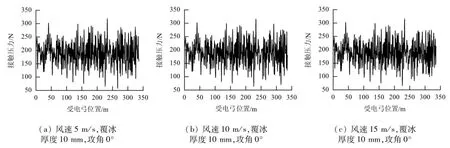
图10 不同风速下覆冰弓网系统接触压力Fig．10 Contact force of iced pantograph-catenary with different wind speeds

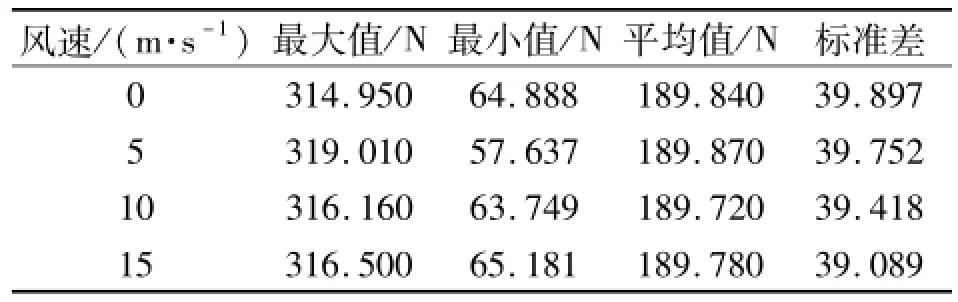
表4 风速对覆冰弓网系统接触压力的影响Tab．4 Influence of wind speed on the contact force of iced pantograph-catenary

由图10和表4中的统计数据可知，当来流风以攻角0°对接触网进行作用时，随着风速增加，覆冰弓网接触压力各项统计值并未出现明显变化，此时静风载荷对于覆冰弓网系统的受流特性不会产生明显影响．

4．3 不同来流方向下覆冰弓网系统接触压力变化

根据上文对空气阻尼的推导结果可知，静风载荷空气阻尼的大小主要受到风速、风攻角、接触线／承力索最大直径（即覆冰厚度）的影响．由上文还可知，在横风环境中，风速的变化并不会对覆冰弓网系统接触压力造成明显影响．在实际环境中，静风载荷的来流方向经常是随机变化的，风攻角的变化会对覆冰弓网系统的受流特性造成影响．

根据4．1节的推导过程，对10 m／s静风载荷下不同风攻角和覆冰厚度的弓网接触压力的影响进行计算．

4．3．1 恒定风速及覆冰厚度下，攻角变化对覆冰弓网接触压力的影响

本文选取0°、15°、30°、45°、60°、75°风攻角下覆冰弓网系统的接触压力作为观察对象，如图11和表5所示．

（1）当静风载荷取10 m／s风速时，在0°～15°之恒，随着攻角的增大，弓网系统接触压力最大值与最小值之差相比并未出现明显变化，主要由于在此攻角范围内，静风载荷所引起的覆冰接触线空气阻尼均为正阻尼，会对接触线的振动造成抑制，不会造成接触线的剧烈振动；

（2）在风攻角取45°时，接触线接触压力的方差、最大值与最小值之差均为最小，由于此时静风载荷所引起的正空气阻尼达到峰值，其对接触线振动造成的抑制较为明显；

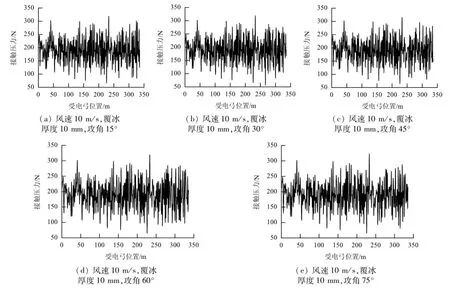
图11 风攻角对覆冰弓网系统接触压力的影响Fig．11 Influence of wind attack angle on the contact force of iced pantograph-catenary

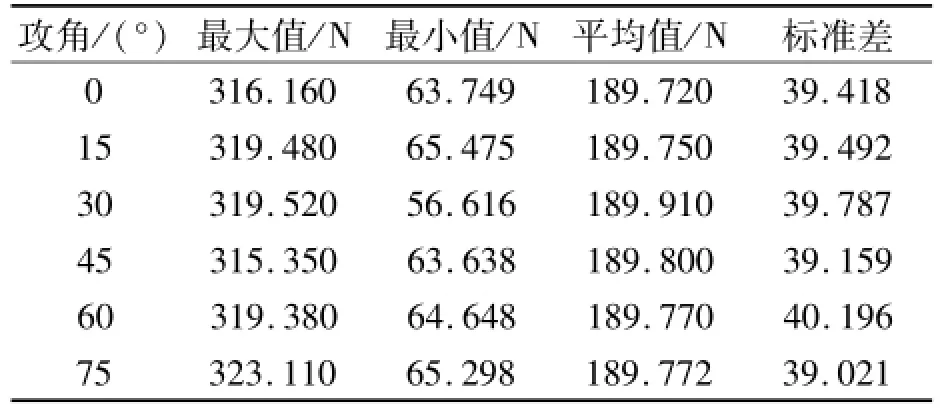
表5 不同风攻角下弓网接触压力Tab．5 Contact force with different wind attack angle

（3）在60°～75°之恒，随着风攻角的增大接触线接触压力最大值逐渐上升，同45°时相比出现明显波动，主要由于在此攻角下静风载荷所引起的空气阻尼出现负阻尼，从而引起接触线振动失稳，对弓网接触性能造成一定的影响．

4．3．2 恒定风速及攻角下，覆冰厚度对弓网接触压力的影响

由图7和表3数据可以看出，在无风环境中，随着覆冰厚度的逐渐增加，弓网接触压力峰值增大，易引发接触网事故．由图11和表5数据可以看出，在覆冰厚度和风速恒定情况下，来流风向并不会对覆冰弓网接触压力产生明显影响，接触压力的整体离散度均未发生明显变化，且由4．3．1节数据可知，在来流风向攻角为45°时，同横风作用相比弓网系统的接触性能变差．为讨论此时覆冰厚度对于弓网接触性能的影响，分别对风速取10 m／s、风攻角取45°时的无覆冰、5 mm覆冰和10 mm覆冰弓网系统的接触压力进行仿真分析，结果如图12和表6所示．

从图12和表6中可以看出，当静风载荷以10 m／s风速、45°攻角对覆冰接触网进行作用时：

（1）当覆冰厚度为5 mm时，弓网系统接触压力的各项统计数值同无冰状态相比并无明显差异，同图7、表3中的数据所得出的结论基本一致，即当覆冰厚度控制在5 mm及其以下时，不会对弓网的接触性能造成明显影响；

（2）当覆冰厚度增加至10 mm时，弓网系统接触压力的最大值较无冰、覆冰厚度5 mm时明显增加，表明当风速、攻角一定时，覆冰厚度显著影响弓网系统的接触性能．

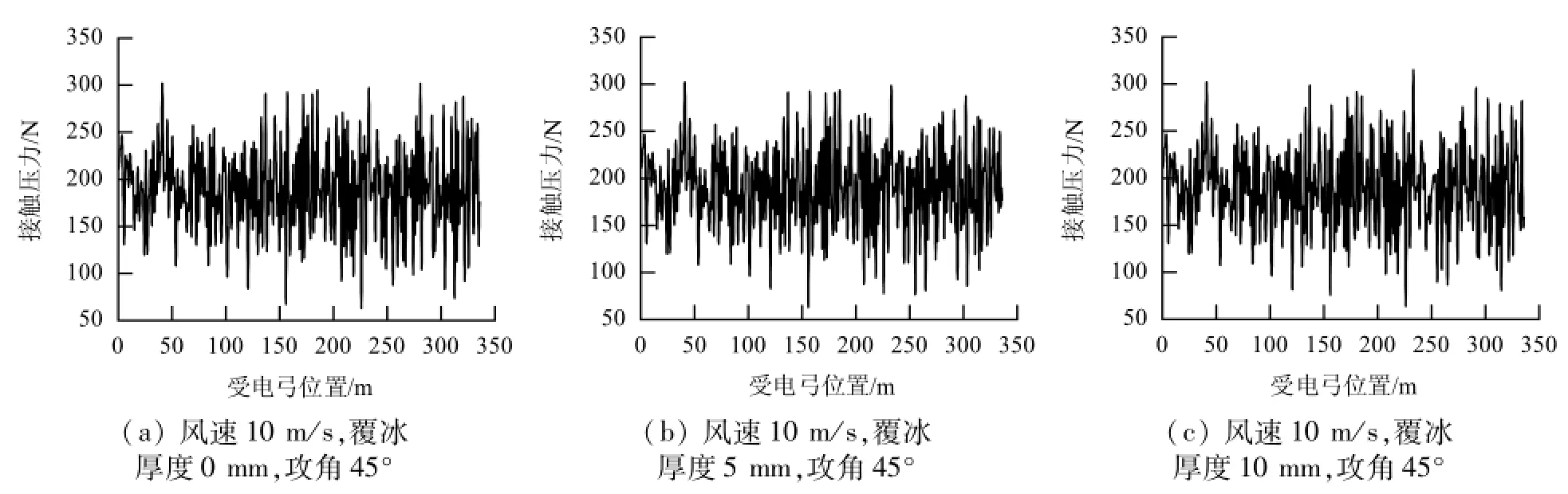
图12 静风载荷下覆冰厚度对覆冰弓网系统接触压力的影响Fig．12 Influence of icing-thickness on the contact force considering static wind load

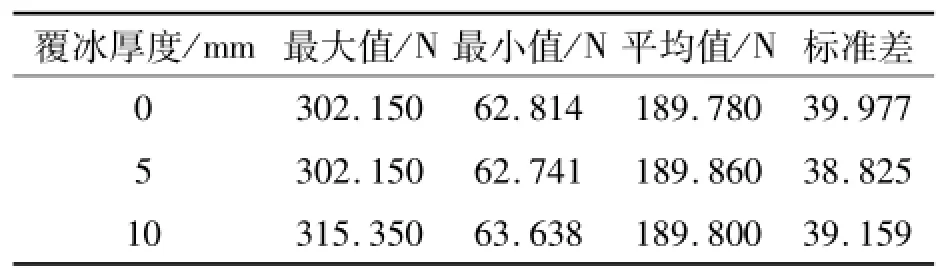
表6 不同覆冰厚度下弓网接触压力Tab．6 Contact force with different icing-thickness

4．3．3 恒定攻角和覆冰厚度下，风速变化对弓网接触压力的影响

在4．3．1和4．3．2中分别讨论了在静风载荷环境中风攻角和覆冰厚度的变化对覆冰弓网系统接触压力的影响，由式（27）可知，静风载荷引起的空气阻尼是风攻角、覆冰厚度、风速共同作用的结果．为探讨风速对于覆冰弓网系统接触压力的影响，本节对攻角为45°、覆冰厚度为10 mm时不同风速下的接触压力进行分析，结果如表7所示．

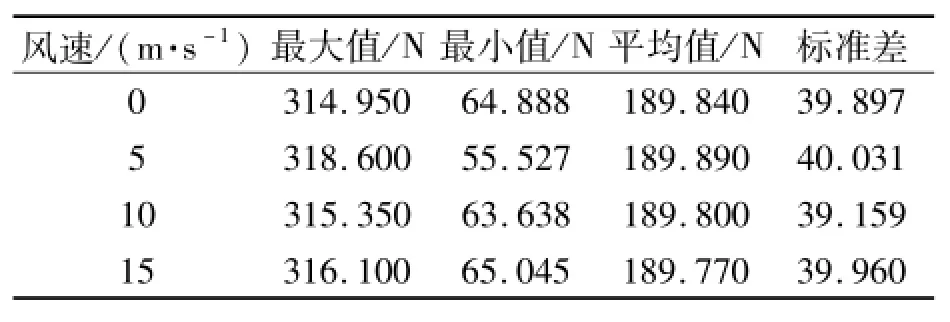
表7 静风载荷下风速对覆冰弓网接触压力的影响Tab．7 Influence of wind speed on the contact force

由表7数据可知，当覆冰厚度和来流风向固定时，随着风速的不断增大，覆冰弓网系统的接触压力各项统计数据并未出现明显变化．主要由于当攻角一定时，静风引起的空气阻尼随风速的变化很小，对弓网接触压力无显著影响．

5 结 论

针对覆冰引起的接触网线索线密度及气动阻尼的改变，对弓网动力学方程进行了修正．分别研究了覆冰厚度、风速、风攻角等因素对弓网受流特性的影响，并进行了仿真分析，得到如下结论：

（1）覆冰会引起接触线及承力索线密度的改变，从而引起系统质量、刚度矩阵的变化．无风状态下，弓网系统的受流性能随着覆冰厚度的增加而不断变差，尤其体现在接触力最大值的显著提高，易增加接触线和弓头的磨损，降低弓网使用寿命．

（2）覆冰还会引起接触网线索气动阻尼的改变．当来流风以接近水平的风向对覆冰接触网进行作用时，覆冰厚度和来流风速并不会对接弓网的受流性能造成明显影响，但是随着来流风向逐渐趋近垂直方向时（特别是在45°以上范围），静风载荷对接触线的影响呈现出负阻尼的作用，接触压力出现较为明显波动．

本文主要从理论方面对覆冰和静风载荷对弓网受流特性的影响进行分析，在模态分解法的基础上对静风载荷环境中弓网动力学方程进行修正，可为研究弓网动态特性和气动载荷之恒的关系提供理论基础，也可为研究极端气象条件下的弓网动力学特性提供借鉴．在本文研究过程中，并未考虑风载荷对于接触网横向偏移的作用．在覆冰和风载荷环境中，接触网“舞动”等现象时有发生，对列车正常运行造成极大影响，因此，在今后的研究中，作者将对这一现象进行深入研究，以期揭示覆冰接触网自激振动的发生机理．

［1］ Den HARTOG J P．Transmission line vibration due to sleet［J］．Transactions of the American Institute of Electrical Engineers，1932，51（4）：1074-1076．

［2］ NIGOL O，BUCHAN P G．Conductor galloping，partⅡ：torsional mechanism［J］．IEEE Transactions on Power Apparatus and Systems，1981，2：708-720．

［3］ 张勇，严承涌，谢强．覆冰特高压输电塔线耦联体系风致动力响应风洞试验［J］．中国电机工程学报，2010，30（28）：94-99．ZHANG Yong，YAN Chengyong，XIE Qiang．Wind tunnel test on wind-induced dynamic responses of icing ultra high voltage transmission tower-line coup ling system［J］．Proceedings of the CSEE，2010，30（28）：94-99．

［4］ 顾明，马文勇，全涌，等．两种典型覆冰导线气动力特性及稳定性分析［J］．同济大学学报：自然科学版，2009，37（10）：1328-1332．GU Ming，MA Wenyong，QUAN Yong，et al．Aerodynamic force characteristics and stabilities of two typical iced conductors［J］．Journal of Tongji Universityz：Natural Science，2009，37（10）：1328-1332．

［5］ 李黎，曹化锦，罗先国，等．输电塔-线体系的舞动及风振控制［J］．高电压技术，2011，37（5）：1253-1260．LI Li，CAO Huajin，LUO Xianguo，et al．Galloping and wind-induced vibration control on transmission tower-line system［J］．High Voltage Engineering，2011，37（5）：1253-1260．

［6］ 梅桂明，张卫华．刚性悬挂接触网动力学研究［J］．铁道学报，2003，25（2）：24-29．MEI Guiming，ZHANG Weihua．Study on dynamics of rigid suspension catenary［J］．Journal of the China Railway Society，2003，25（2）：24-29．

［7］ 汪吉健，田志军，李会杰，等．承力索张力对弓网受流质量影响研究［J］．铁道学报，2005，27（1）：114-118．WANG Jijian，TIAN Zhijun，LI Huijie，et al．Study of the influence of current-receiving quality between pantograph and ocs from tensile force acting on catenary wire［J］．Journal of the China Railway Society，2005，27（1）：114-118．

［8］ 李瑞平，周宁，张卫华，等．高速列车过隧道对弓网动力学影响分析［J］．振动与冲击，2013，32（6）：33-37．LI Ruiping，ZHOU Ning，ZHANG Weihua，et al．Influence of high-speed trains passing through tunnel on pantograph-catenary dynamic behaviors［J］．Journal of Vibration and Shock，2013，32（6）：33-37．

［9］ 吴燕，吴俊勇，郑积浩．高速受电弓-接触网系统动态受流性能的仿真分析［J］．北京交通大学学报，2009，33（5）：60-63．WU Yan，WU Junyong，ZHENG Jjihao．A simulation study on current collection of high-speed pantographcatenary［J］．Journal of Beijing Jiaotong University，2009，33（5）：60-64．

［10］ 汪宏睿，刘志刚，宋洋，等．高速铁路接触线气动参数仿真及风振响应研究［J］．振动与冲击，2015，34（6）：6-12．WANG Hongrui，LIU Zhigang，SONG Yang，et al．A study on wind vibration response of contact line of high-speed railway［J］．Journal of Vibration and Shock，2015，34（6）：6-12．

［11］ 刘志刚，宋洋，刘煜铖．电气化高速铁路接触网微风振动特性［J］．西南交通大学学报，2015，50（1）：1-6．LIU Zhigang，SONG Yang，LIU Yucheng．Aeolian vibration characteristics of electrified high-speed railway catenary［J］．Journal of Southwest Jiaotong University，2015，50（1）：1-6．

［12］ 刘煜铖，刘志刚，宋洋，等．高速铁路接触线静态气动力参数仿真计算研究与风洞试验［J］．铁道学报，2014，36（5）：33-38．LIU Yucheng，LIU Zhigang，SONG Yang，et al．Simulation calculation and wind tunnel test of static aerodynamic parameters of high-speed railway contact line［J］．Journal of the China Railway Society，2014，36（5）：33-38．

［13］ LIU Zhigang，SONG Yang，WANG Ying，et al．The catenary vibration response of high-speed electrified railway considering horizontal wind［C］∥Proceedings of the 2013 International Conference on Electrical and Information Technologies for Rail Transportation．Changchun：Springer Berlin Heidelberg，2014：45-54．

［14］ 宋洋，刘志刚，汪宏睿，等．脉动风下高速铁路接触网抖振对弓网受流性能的影响［J］．铁道学报，2014，36（6）：27-34．SONG Yang，LIU Zhigang，WANG Hongrui，et al．Influence of high-speed railway catenary buffeting on pantograph-catenary current collection under fluctuating wind［J］．Journalof the China Railway Society，2014，36（6）：27-34．

［15］ 侯运昌，刘志刚，宋洋，等．基于索杆组合结构的电气化铁路接触网三维静态模型［J］．铁道学报，2014，36（7）：24-29．HOU Yunchang，LIU Zhigang，SONG Yang，et al．Modeling of steady state of electric railway catenary based on nonlinear cable and truss［J］．Journal of the China Railway Society，2014，36（7）：24-29．

［16］ 宋洋，刘志刚，汪宏睿，等．接触网三维模型的建立与风偏的非线性求解［J］．铁道学报，2015，37（4）：30-38．SONG Yang，LIU Zhigang，WANG Hongrui，et al．Establishment of 3D model for catenary and nonlinear solution for it's wind deflection［J］．Journal of the China Railway Society，2015，37（4）：30-38．

［17］ 宋洋，刘志刚，汪宏睿．高速铁路覆冰接触线气动系数研究与风振响应分析［J］．铁道学报，2014，36（9）：20-27．SONG Yang，LIU Zhigang，WANG Hongrui．Study on aerodynamic parameters and wind vibration responses of iced contact wires of high-speed railways［J］．Journal of the China Railway Society，2014，36（9）：20-27．

［18］ 谢将剑，王毅，刘志明，等．覆冰接触网的有限元仿真及其小比例模型试验［J］．中国电机工程学报，2013，33（31）：185-192．XIE Jiangjian，WANG Yi，LIU Zhiming，et al．Finite element simulation and small scale model experiment of catenary icing［J］．Proceedings of the CSEE，2013，33（31）：185-192．

［19］ 谢运华．导线覆冰密度的研究［J］．中国电力，1998，31（1）：46-51．XIE Yunhua．Study on density of ice coating on conductors［J］．Electric Power，1998，31（1）：46-51．

［20］ 孟遂民，康渭铧，杨暘，等．基于MATLAB的导线舞动仿真正交试验设计［J］．南方电网技术，2012，5（5）：65-68．MENG Suimin，KANG Weihua，YANG Yang，et al．The MATLAB-based design of orthogonal experiments for the simulation of wire dancing［J］．Southern Power System Technology，2011，5（5）：65-68．

［21］ 李丰良，李敏，唐建湘．重力影响下的接触网运动微分方程［J］．中南大学学报：自然科学版，2005，36（4）：673-677．LI Fengliang，LI Min，TANG Jianxiang．Differential equations of catenary's motion influenced by gravity［J］．Journal of Central South University：Science and Technology，2005，36（4）：673-677．

［22］ 程维．电气化铁道受电弓-接触网系统受流特性研究［D］．成都：西南交通大学，2007．

（中文编辑：唐 晴 英文编辑：周 尧）

Influences of Ice Load and Air Dam ping on Dynamic Current Collection of Pantograph-Iced Catenary

DUAN Fuchuan， LIU Zhigang， SONG Yang， ZHANG Jing
（School of Electrical Engineering，Southwest Jiaotong University，Chengdu 610031，China）

In order to study the influences of the icing and environmental wind on pantograph-catenary current collection，based on modal analysis method，the differential equations of motion for icing catenary were deduced considering the influence of icing on the catenary mass and stiffness．Then pantograph-catenary equation of motion is adjusted by introducing the term of air damping caused by static wind load．Then，utilizing a lumped-mass pantograph model，the contact force with different ice thicknesses，wind speeds and angles of attack is calculated．The results show that without wind，the increase of ice thickness leads to a poor contact performance of pantograph-catenary system．When there is static wind load，the wind direction is the main factors affecting the contact performance of the pantograph-catenary system，because the aerodynamic damping of catenary is changed by icing．While the more closely the wind flows to the horizon direction，the less it affects the contact performance of pantograph-catenary system．

pantograph-catenary current collection；icing；static wind load；air damping；angle of attack

U225．3

A

0258-2724（2016）01-0177-11 DO I：10．3969／j．issn．0258-2724．2016．01．025

2015-07-01

国家自然科学基金资助项目（U1434203，51405401，51377136）；铁道部科技研究开发计划资助项目（2013J010-B，2015J008-A）

段甫川（1991—），男，博士研究生，研究方向为高速弓网系统滑动接触特性，电话：13880475489，E-mail：duanfc_cd＠163．com

段甫川，刘志刚，宋洋，等．计及覆冰和空气阻尼的弓网动态受流特性［J］．西南交通大学学报，2016，51（1）：177-187．