行人交通流三参数基本关系式适用性研究

叶建红， 陈小鸿

（同济大学教育部道路与交通工程重点实验室，上海201804）

行人交通流三参数基本关系式适用性研究

叶建红， 陈小鸿

（同济大学教育部道路与交通工程重点实验室，上海201804）

为研究交通流量、密度和速度基本关系式对行人交通流的适用性，采用类比和误差分析方法，建立了行人交通流基本关系式评价方法与步骤．采集了水平通道、楼梯等步行设施行人流量、密度和速度数据，并利用基本关系式进行密度换算，分析了密度实际观测值与基本关系式换算值之间的差异．研究结果表明：对于有固定边界步行设施上的行人交通流，在极低密度和极高密度时，用基本关系式换算参数的误差可高达20%～25%；使用基本关系式还会得到极高密度时行人交通仍能获得较高流量与速度的错误结论，并导致部分高密度交通流数据缺失；行人交通流三参数基本关系式并不严格成立，对于行人通行能力的理论研究，不应采用基本关系式进行参数换算．

行人交通；交通流参数；基本关系式；适用性

交通流三参数基本关系式，即流量＝密度×速度，是交通工程研究与实践的基础．然而，交通流基本关系式成立有严苛的前提条件．文献［1］将这些条件概括为：交通流可以被划分为若干个子交通流，每个子交通流的车辆具有相同的速度和空间间隔．在实际交通运行状态下，这些条件很难满足，尤其是处于拥挤状况时，上述条件不成立．因此，交通流参数基本关系式在现实交通中有误用现象［1］．

行人交通流研究中也常利用该基本关系式进行参数观测与建模分析．对行人交通流参数基本关系的研究始于20世纪50年代后期，通过人工观测、摄像记录等手段获取行人流移动的特征数据，再利用统计方法建立行人流量、速度与密度之间关系模型．在建模过程中，大多数研究首先利用线性或非线性函数拟合速度与密度之间的关系，然后通过基本关系式得到流量与速度、流量与密度之间的关系［2-13］．也有少数研究未采用该基本关系式，使用多项式、BPR（bureau of public road）函数等模型直接拟合流量与速度、流量与密度的关系［14-18］．

目前对行人交通流三参数基本关系已有了一些研究成果，但对于交通流特征参数的观测与统计方法却缺乏规范的、一致性的数据分析规则，这是导致不同学者得到的交通流参数关系模型及特征值差异很大的重要原因之一，例如，对同类步行设施，其通行能力变化范围为1．2～1．8人／（m·s），最佳密度变化范围为1．75～7．00人／m2，阻塞密度变化范围为3．8～10．0人／m2［19］．

机动车交通流基本关系式成立需要一定的前提条件，对于行人交通流基本关系式的适用条件，及其在实际交通运行状态下的适用性，目前还缺乏充分的研究．本文以实际行人交通流为分析对象，研究基本关系式对行人交通流的适用性．首先根据流量、密度和速度的定义独立观测3个参数，得到观测值．然后，以密度换算为例（密度不易直接观测，很多研究都利用基本关系式换算密度），比较密度观测值与根据基本关系式得到的密度换算值之间的差异，分析密度换算的误差范围，给出实际行人交通流基本关系式的适用条件．

1 数据采集

1．1 观测对象

为了获取出行目的单一、不受其它交通方式干扰、且涵盖较大密度范围的行人交通流参数，选取轨道交通车站内的行人交通为观测对象，并以客流量大的上海市轨道交通1号线人民广场站和2号线中山公园站作为观测场所．这两个车站均为三线换乘站，2009年日均客流量分别达到58万人次和24万人次，高峰小时客流约占全天客流总量的20%［16］．在人民广场站内选择了一段单向水平通道和一段双向水平通道，在中山公园站内选择了一组上行楼梯和一组下行楼梯作为观测设施．通常情况下所观测的两组楼梯均为单向通行，但部分时段两组楼梯上也存在双向通行的人流，故将这些双向通行的时段单独选出来作为双向楼梯进行分析．各类观测设施的物理特征如表1和图1所示．

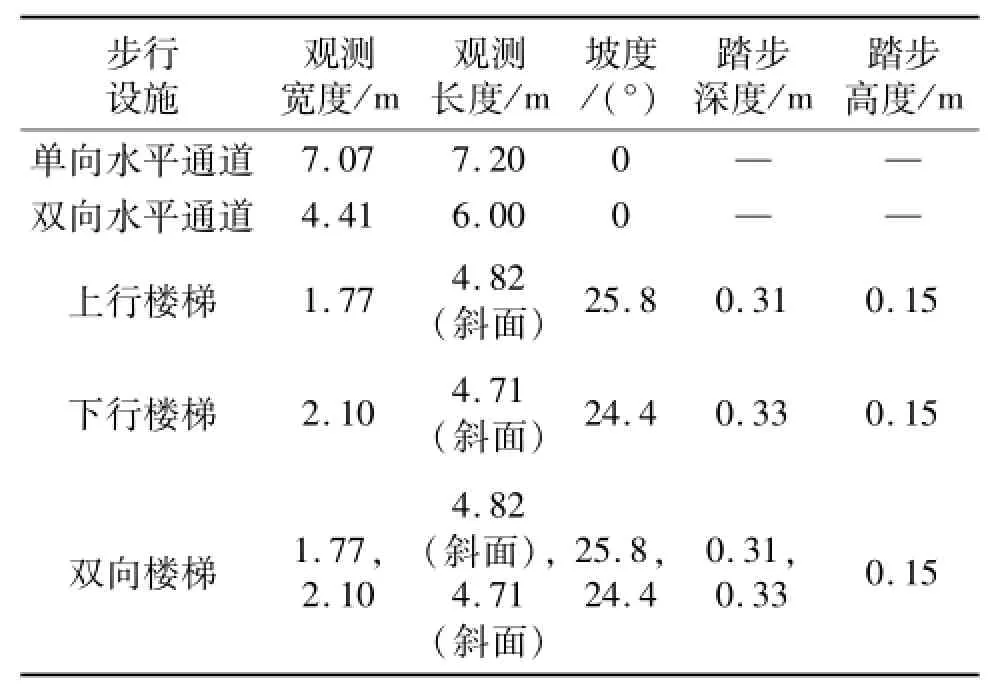
表1 5类观测设施物理特征Tab．1 Physical parameters of five kinds of walking facilities for observation

图1 观测设施实拍图Fig．1 Photos of the observed walking facilities

1．2 交通流参数采集

在工作日出行高峰时段（上午7：00～10：00，下午4：00～7：00）对各类步行设施进行视频拍摄，得到各类设施近6 h的行人交通流视频录像．在后期视频图像处理中，为获取准确度高的数据，采用了人工统计方式从视频录像中提取行人流量、密度、速度等交通流参数．当人流密度较低时，以正常播放速度播放录像进行参数统计；当人流密度较高时，以正常速度播放视频来获取参数值较困难，故采取慢速甚至逐帧播放视频的方法进行参数统计．以30 s为统计间隔［20］，独立统计5类步行设施的行人流量、密度和速度3个参数．各参数的计算方法如下：

（1）流量．统计30 s内通过步行设施观测区域端部横断面的行人数（对于双向通道则是两个方向行人数之和），基于设施宽度可得到单位宽度单位时间内通过观测断面的人数，即流量值，单位：人／（min·m）．

（2）密度．根据密度定义，只需统计观测间隔内任一瞬间观测区域范围内的行人数以计算密度．考虑到30 s内行人密度可能有波动及抽样偏差，在30 s内随机抽取了15个瞬间（每2 s随机取1个瞬间），统计每个瞬间观测范围内的行人数；然后，取这15个瞬间行人数的算术平均值作为30 s内任一瞬间的平均行人数；最后，将此平均行人数除以观测区域面积得到密度值，单位：人／m2．

（3）速度．根据速度定义，应统计观测间隔内所有经过观测设施范围的行人移动速度．但对于人工统计来说，严格按照速度定义进行全样本统计工作量过大．由于选取的观测场所、对象已经保证了行人流动目的的一致性和连续性，因此，在30 s间隔内随机选取了15个行人（每2 s随机选择1个行人．当人流量低、30 s间隔内不足15个人时，进行全样本统计）进行速度观测．分别记录这15个行人在观测时间间隔和观测空间范围内行走的距离及行走时间，再将这15个人的行走距离之和除以行走时间之和，得到空间平均速度，单位：m／min．

2 密度换算适用性分析方法

2．1 分析思路

在行人流量、密度和速度3个参数中，密度值很难通过现场人工观测手段直接获取，因此，文献［2-13］均通过实测流量和速度，再利用基本关系式换算得到密度．为了检验这种换算方法的适用性，需要分析密度换算的误差．当误差值可接受时，说明交通流基本关系式具有较好的适用性，反之则适用性差．本文对误差可接受程度的判断主要根据两个方面：

（1）交通流参数关系曲线的误差分析，即评估密度换算对交通流参数关系图（形状、趋势等）的影响；

（2）数值误差分析，即评估换算密度与实测密度之间的差异（绝对误差、相对误差等）．

2．2 分析步骤

采取如下步骤分析密度换算的适用性：

（1）比较交通流参数关系图的差异．分别采用实测密度Dm和换算密度Dc绘制各类步行设施行人交通流量-密度、速度-密度关系散点图，根据图形形状、延展趋势等，直观判断由这两类密度得到的同一类散点图是否存在显著差异．

（2）比较两类密度的数值差异．对实测密度进行分组，计算各组实测密度与换算密度的绝对误差（Dc－Dm）和相对误差（（Dc－Dm）／Dm）．结合误差置信区间，定量分析不同密度范围交通流基本关系换算式的适用性．

（3）综合考虑密度换算对交通流参数关系图的影响以及换算数值的差异，给出行人交通流基本关系式的适用性评估结论．

3 各类步行设施密度换算适用性分析

3．1 交通流参数关系差异

分别用实测密度和换算密度绘制单向水平通道、双向水平通道、上行楼梯、下行楼梯和双向楼梯的流量-密度、速度-密度关系散点图，如图2～6所示．

由图2～6可见，除双向水平通道外（观测到的密度数据范围有限），单向水平通道、上行楼梯、下行楼梯和双向楼梯的两类密度交通流散点图在部分密度区间都存在显著差异（图2、图4～6中矩形框中部分），具体如下：

（1）在各类设施中、高密度范围内，由换算密度和实测密度得到的两类交通流散点图存在较大差异．

（2）对于单向水平通道、上行楼梯和双向楼梯，换算得到的流量-密度曲线与速度-密度曲线较相应实测曲线均沿密度轴延伸了范围，且这种延伸有背离实测曲线变化规律的趋势．换言之，通过密度换算得到了实际观测中并未出现的高密度值．

（3）换算得到的下行楼梯流量-密度曲线与速度-密度曲线较相应实测曲线沿密度轴缩小了范围，即换算后的密度小于实测密度，部分高密度数据丢失．

图3 双向水平通道两种密度交通流散点图Fig．3 Scatter plot comparison of two pedestrian traffic flows with different densities for two-way passageway

图4 上行楼梯两种密度交通流散点图Fig．4 Scatter plot comparison of two pedestrian traffic flowswith different densities for ascending stairway

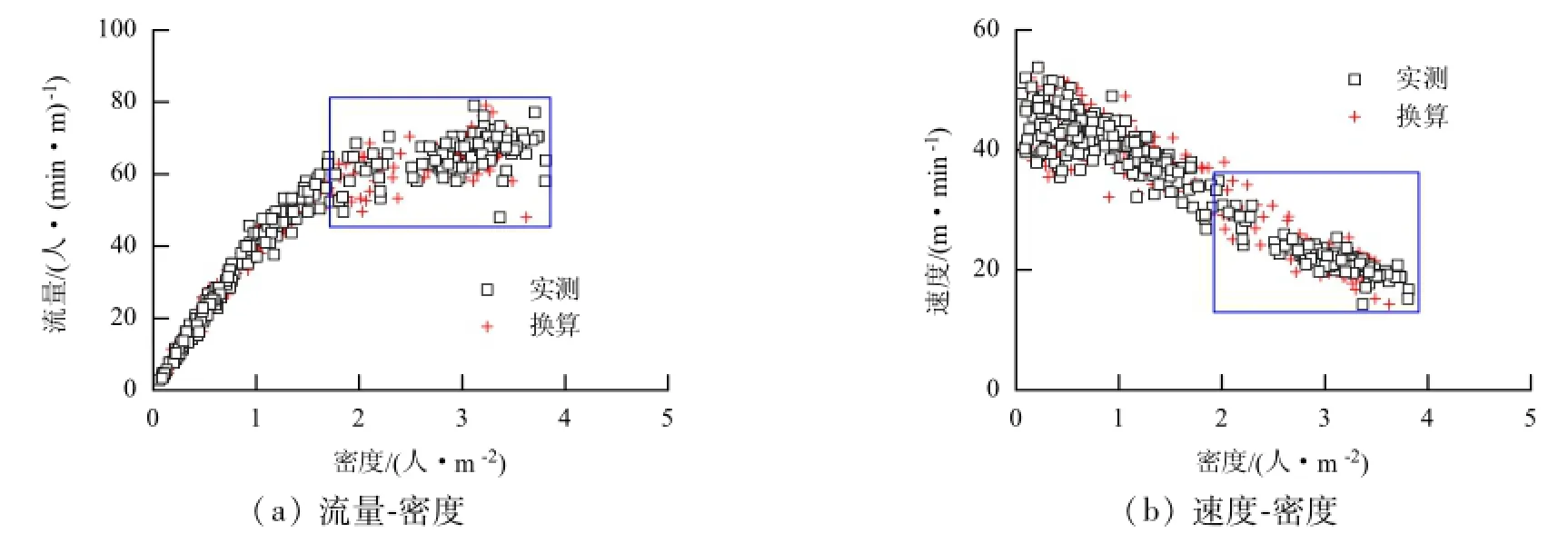
图5 下行楼梯两种密度交通流散点图Fig．5 Scatter plot comparison of two pedestrian traffic flows with different densities for descending stairway

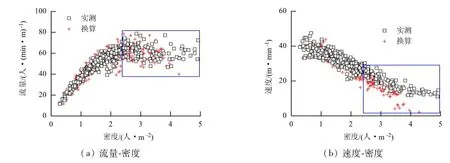
图6 双向楼梯两种密度交通流散点图Fig．6 Scatter plot comparison of two pedestrian traffic flows with different densities for two-way stairway

3．2 两类密度的数值差异

分别针对单向水平通道、双向水平通道、上行楼梯、下行楼梯和双向楼梯，计算换算密度与实测密度的绝对误差与相对误差，如图7和表2所示．

图7 各类步行设施换算密度相对误差Fig．7 Relative errors of calculated densities for differentwalking facilities

根据图7和表2换算密度的误差分析可以得到：

（1）各类步行设施大都出现了密度换算误差大于10%的密度层，如单向水平通道在（1．0，1．5］密度层、上行楼梯在（1．5，2．5］密度层、双向楼梯在（3．0，3．5］密度层时，其换算密度的相对误差均超过10%．

（2）极低密度（小于0．5人／m2）和极高密度（大于2．5人／m2）时，各类设施换算密度相对误差都呈现扩大趋势．参照机动车交通流基本关系式成立的假设条件，低密度时行人流中个体间隔随机变化，不能很好满足个体间隔保持不变的要求；高密度时行人个体速度和间隔都在不断变化，假设条件也不满足，故换算密度误差大．

（3）单向水平通道、双向水平通道、下行楼梯的换算密度小于实际观测密度，上行楼梯和双向楼梯的换算密度总体上大于实测密度，但在低密度时（小于0．5人／m2）小于实测密度．

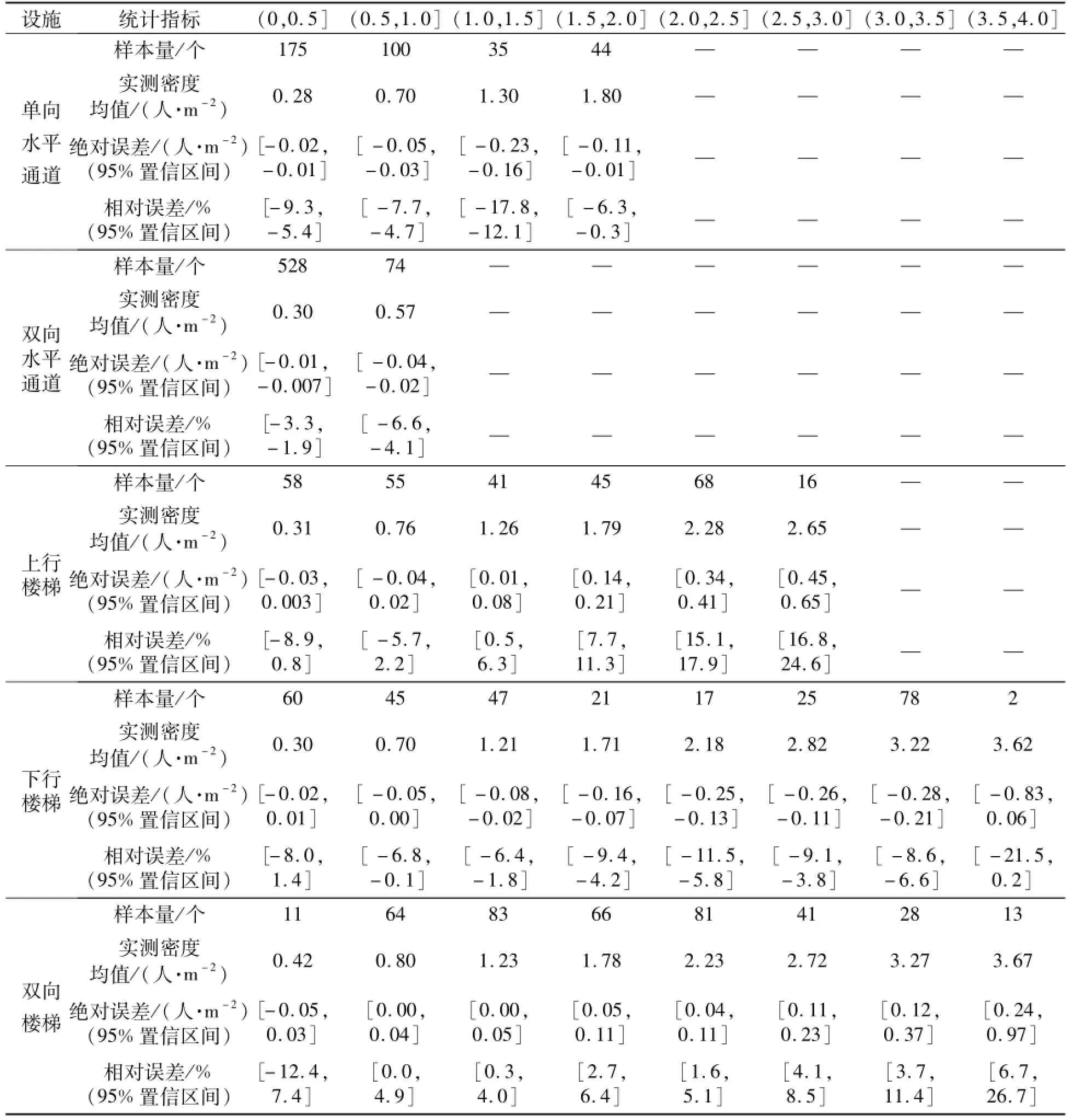
表2 各类步行设施不同密度组的换算密度误差分析Tab．2 Relative errors of calculated densities in different density groups for different walking facilities

4 结束语

通过密度换算的误差分析，对5类步行设施交通流基本关系式的适用性总结如下：

（1）对单向水平通道、上行楼梯和双向楼梯，通过交通流参数基本关系换算得到的流量-密度和速度-密度曲线较相应实测曲线均沿密度轴延伸了范围，且这种延伸有背离实测曲线变化规律的趋势；对下行楼梯换算得到的流量-密度与速度-密度曲线较相应实测曲线沿密度轴缩小了范围，密度换算后丢失了部分高密度交通流数据．

（2）分析换算密度与实测密度的误差可知，极低密度和极高密度时换算密度相对误差大，交通流基本关系式适用性差；单向水平通道、双向水平通道、下行楼梯的换算密度小于实际观测密度，上行楼梯和双向楼梯的换算密度总体上大于实测密度．

因此，对于在有固定边界步行设施上运行的行人交通流，基本关系式密度＝流量／速度并不严格成立，各类步行设施实测密度与换算密度均有不同程度的差异．更重要的是，对于单向水平通道、上行楼梯和双向楼梯，用换算密度得到的流量-密度和速度-密度曲线较实测曲线沿密度轴延伸，且与实测曲线的变化趋势不一致，会得到误导研究人员的结论：在极高密度时行人流仍能获得较高的流量与速度值．这个误导性的结论对步行设施设计以及高密度人流的安全集散评估都会埋下安全隐患．而对于下行楼梯，使用密度换算导致部分高密度交通流数据缺失，不利于开展设施通行能力研究．

开展行人交通流理论研究，需要关注最大通行能力附近的高密度行人交通流特性，以此作为确定设施通行能力及评估设施设计安全性的基础．因此，采用实测密度而非换算密度可避免错误结论．

致谢：本研究依托于大量现场观测与视频数据，为此特别感谢上海申通集团提供的车站监控视频以及对现场调查给予的帮助．

［1］ GARTNER N，MESSER C J，RATHI A K．Revised monograph on traffic flow theory［M］．Washington D．C．：The Federal Highway Administration（FHWA），2002：2-1-2-36．

［2］ OLDER S J．Movement of pedestrians on footways in shopping streets［J］．Traffic Engineering and Control，1968，10：160-163．

［3］ OEDING D．Traffic loads and dimensions of walkways and other pedestrian circulation facilities［J］．Strassenbau und Strassenverkehrstechnik，1963（22）：160-163．

［4］ NAVIN P D，WHEELER R J．Pedestrian flow characteristics［J］．Traffic Engineering，1969：30-36．

［5］ FRUIN J J．Pedestrian planning and design［M］．Mobile：Elevator World，1987：37-87．

［6］ O'FLAHERTY CA，PARKINSONM H．Movementon a city centre footway［J］．Traffic Engineering and Control，1972，13，434-438．

［7］ POLUSA SHOFER J L，USHPIZ A．Pedestrian flow and level of service［J］．Journal of Transportation Engineering，1983，109（1）：46-56．

［8］ KHISTY C J．Pedestrian flow characteristics on stairways during disaster evacuation［J］．Transportation Research Record，1985，1047：97-102．

［9］ TANABORIBOON Y，HWA S S，CHOR C H．Pedestrian characteristics study in Singapore［J］．Journal of Transportation Engineering，1986，112（3）：229-235．

［10］ PAULS J．Building evacuation：research finding and recommendations［M］．2nd ed．London：Letts Educational，1990：251-275．

［11］ GERILLA G P，HOKAO K，TAKEYAMA Y．Proposed level of service standards for walkways in metro manila［J］．Journal of the Eastern Asia Society for Transportation Studies，1995，1（3）：1041-1060．

［12］ LAM W H K，MORRALL JF，HO H．Pedestrian flow characteristics in Hong Kong［J］．Transportation Research Record，1995，1487：56-62．

［13］ SARKAR A K，JANARDHAN K S V S．Pedestrian flow characteristics at an intermodal transfer terminal in Calcutta［J］．World Transport Policy and Practice，2000，6（3）：32-38．

［14］ DAL Y P N，MCGRATH F，ANNESLEY T J．Pedestrian speed／flow relationships for underground stations［J］．Traffic Engineering and Control，1991，32（2）：75-78．

［15］ AL-MASAEID H R，AL-SULEIMAN T I，NELSON D C．Pedestrian speed-flow relationship for central business district areas in developing countries［J］．Transportation Research Record，1993，1396：69-74．

［16］ CHEN Xiaohong，YE Jianhong，JIAN Nanjing．Relationships and characteristics of pedestrian traffic flow in confined passageways［J］．Transportation Research Record，2010，2198：32-40．

［17］ 史建港．大型活动行人交通特性研究［D］．北京：北京工业大学，2007．

［18］ 柳伍生，余朝玮．地铁站楼梯行人流交通特征的数据拟合分析［J］．计算机工程与应用，2008，44（3）：50-52．LIU Wusheng，YU Chaowei．Analyzing to characteristics of pedestrians flow on stairways atmetro transfer stations basing on data fitting［J］．Computer Engineering and Applications，2008，44（3）：50-52．

［19］ SCHADSCHNEIDER A，KLINGSCH W，KLÜPFEL H．et al．Evacuation dynamics：empirical，results，modeling and applications in encyclopedia of complexity and system Science［M］．New York：Springer，2009：3142-3176．

［20］ YE Jianhong，CHEN Xiaohong．Optimal measurement interval for pedestrian traffic flow modeling［J］．ASCE Journal of Transportation Engineering，2011，137（12）：934-943．

（中文编辑：秦萍玲 英文编辑：兰俊思）

Applicability Analysis of Triparametric Fundamental Equations for Pedestrian Traffic Flow

YE Jianhong， CHEN Xiaohong
（Key Laboratory of Road and Traffic Engineering of the Ministry of Education，Tongji University，Shanghai 201804，China）

To verify whether the fundamental equations among traffic volume，density and speed hold for pedestrian traffic flow，methods of analogy analysis and error analysis were used to establish the methodology and procedures for examining the applicability of the fundamental equations．Pedestrian traffic data including volume，density，and speed on level walkways and stairways were collected．The observed density values were compared with those converted by the fundamental equations to analyze the errors between them．The results show that for the pedestrian flow on walking facilities with boundaries，the relative error of parameter conversion by using the fundamental equations could reach more than 20%－25%in very low and high density conditions．What's worse，the application of fundamental equations likely leads to a wrong conclusion that the pedestrian flow and speed can be still high in high density conditions，and even loses some high-density data．The truth is that the traffic flow fundamental equations do not hold strictly under real pedestrian traffic conditions，and hence should not be applied for parametric calculation in theoretical research of pedestrian traffic capacity．

pedestrian traffic；traffic flow parameters；fundamental equations；applicability

U491．22

A

0258-2724（2016）01-0138-07

10．3969／j．issn．0258-2724．2016．01．020

2014-11-03

国家自然科学基金资助项目（51108342）

叶建红（1981—），男，副教授，博士，研究方向为交通运输系统规划与管理、行人交通流理论与组织管理，电话：13916427320，E-mail：yjh1875＠hotmail．com

叶建红，陈小鸿．行人交通流三参数基本关系式适用性研究［J］．西南交通大学学报，2016，51（1）：138-144．