RC框架-内填带竖缝剪力墙结构的滞回性能及计算模型研究①

肖 魁, 张其林

(1. 上海建筑设计研究院有限公司， 上海 200041;2. 同济大学土木工程学院， 上海 200092)

RC框架-内填带竖缝剪力墙结构的滞回性能及计算模型研究①

肖 魁1,2, 张其林2

(1. 上海建筑设计研究院有限公司， 上海 200041;2. 同济大学土木工程学院， 上海 200092)

为研究钢筋混凝土框架-内填带竖缝剪力墙(RCFW)结构的抗震性能，对两个单跨两层、缩尺比为1∶2的RCFW试件进行了拟静力试验研究。结合RCFW结构在往复荷载作用下的响应特性，提出了适用于RCFW结构弹塑性分析的带刚臂纤维截面计算模型，并基于有限元程序ABAQUS提供的用户子程序接口UMAT，开发了混凝土、钢筋两种材料的单轴滞回本构模型，从材料本构层次直接反映构件层次的恢复力特性。通过与RCFW结构低周反复荷载试验结果的对比，验证了计算模型的准确性，模拟曲线较好地反映了RCFW结构在反复加载过程中荷载-位移曲线的承载力和刚度退化及捏拢现象；此外，该计算模型还具有高效的求解效率和数值稳定性，适用于RCFW结构的弹塑性分析和整体抗震性能评估。

竖缝剪力墙； 滞回； 纤维截面模型； 本构模型； UMAT

引 言

RCFW结构(全称 Reinforced Concrete Frame with Infill Slit Shear Walls)是由RC框架和内填带竖缝墙体通过抗剪连接件组合而成的一种新型结构体系。由于设置了预制竖缝，在水平地震作用下，内填墙的各缝间墙肢以弯曲变形为主，墙体抗侧刚度减弱，产生大量分布面广的细小裂缝，延性和耗能能力增强。目前，针对RCFW结构抗震性能的试验研究和分析方法还鲜见报道。

叶列平[1-2]等研究了混凝土框架-内嵌通缝剪力墙结构的抗震性能，框架与内嵌通缝墙之间采用整体式浇筑。并采用由质量块和剪切弹簧等组成的单自由度宏模型，结合三线性Takeda恢复力滞回规则[3]，编程计算了其弹塑性地震响应。计算结果较好地反映了整体结构的刚度退化和捏拢行为，但是宏模型过于简化，不能反映地震作用下各构件的内力分配和非线性反应特性。米旭峰[4]基于ANSYS软件模拟了钢框架内嵌带竖缝剪力墙结构的单调加载过程，并将竖缝剪力墙简化为壁式框架，提出了适用于单调加载分析的壁式框架分析模型，该模型能较为真实地反映整体结构的性能和各构件的内力分配，但由于壁式框架模型较复杂，给有限元实现带来了一定的困难。Rassati[5]等建立了半刚接钢框架内填混凝土剪力墙(SRCW)结构的三维有限元模型，通过钢-混凝土界面单元来考虑钢框架和内填墙之间的接触和滑移效应，采用由扭转弹簧和线弹簧组成的宏单元来模拟半刚性节点。该模型可较好地模拟结构单调加载曲线的峰后承载力下降段，但模型过于复杂，需要大量的参数标定和计算机时的耗费。

本文针对RCFW这一新型结构体系，基于1∶2缩尺试件的低周反复荷载试验，分析了RCFW结构的滞回耗能性能，并提出了适用于RCFW结构弹塑性分析的带刚臂纤维截面计算模型，基于有限元程序ABAQUS提供的用户子程序接口UMAT，开发了混凝土、钢筋两种材料的单轴滞回本构模型，从材料本构层次直接反映构件层次的恢复力特性。此外，为方便对比，还建立了RCFW结构的精细化实体模型，结合混凝土和钢材多轴滞回本构进行了模拟计算。将模拟结果分别与试验结果进行比较，对比了两种计算模型的计算精度和效率，结果表明：实体模型计算效率较低，且虽然在材料模型中考虑了弹性损伤，但仍过高地估计了结构的加卸载刚度，计算得到的滞回曲线偏于饱满；而采用带刚臂纤维截面计算模型结合本文开发的UMAT材料滞回本构，可以较为真实地模拟循环荷载下RCFW结构的整体滞回性能。

1 RCFW结构计算模型及纤维截面本构

1.1 实际结构及计算模型的建立

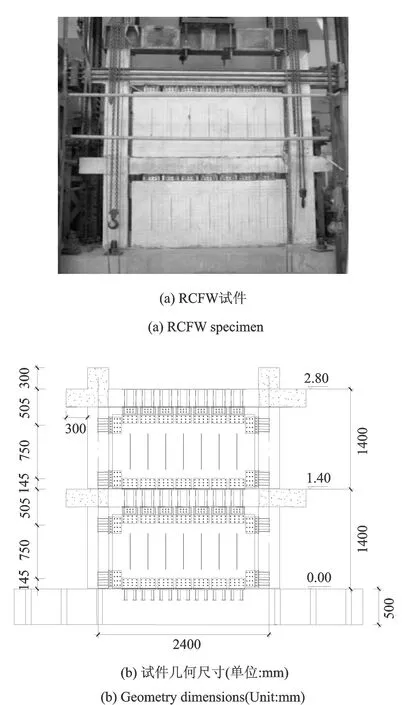
图1 RCFW结构试件及几何尺寸Fig.1 Specimen and detail dimensions

设计了2榀几何尺寸相同的单跨两层、缩尺比1∶2的RCFW试件，试件编号为RCFW-1和RCFW-2，分别采用不同的设计轴压比0.2和0.3，并进行了低周反复加载试验。试件形式及尺寸如图1所示，层高1.4 m，跨度2.4 m。框架梁截面为150 mm×250 mm，梁端顶部受拉纵筋6C10，底部受力纵筋410，箍筋沿梁全长加密，采用6@50双肢箍；框架柱截面为300 mm×300 mm，纵向钢筋为12 12+4 8，箍筋沿柱全长加密，采用6@50复合井子箍。竖缝剪力墙板的设计参照JGJ99-98《高层民用建筑钢结构技术规程》[6]，墙板厚100 mm，共设置7条竖缝，缝间距250 mm，缝高×宽为500 mm×5 mm，内填石棉板。墙体配筋详图如图2所示，采用双层钢筋网片，实体墙每侧受力纵筋2 8，竖向和水平分布筋均为 6@75；缝间墙段每侧受力纵筋1 8+1 6，箍筋为 6@75。竖缝剪力墙和框架之间的刚性抗剪连接件采用Q345B镇静钢制作，由预埋钢板、预埋角钢及连接钢板组成。试件基座高500 mm，采用防滑移装置与实验室地槽锚固。各构件材料参数如表1所示。

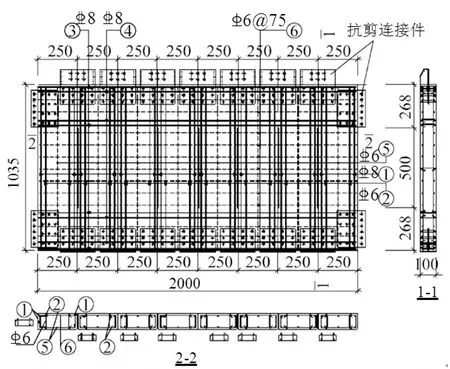
图2 竖缝剪力墙板配筋详图Fig.2 Reinforcement details of the slit shear wall

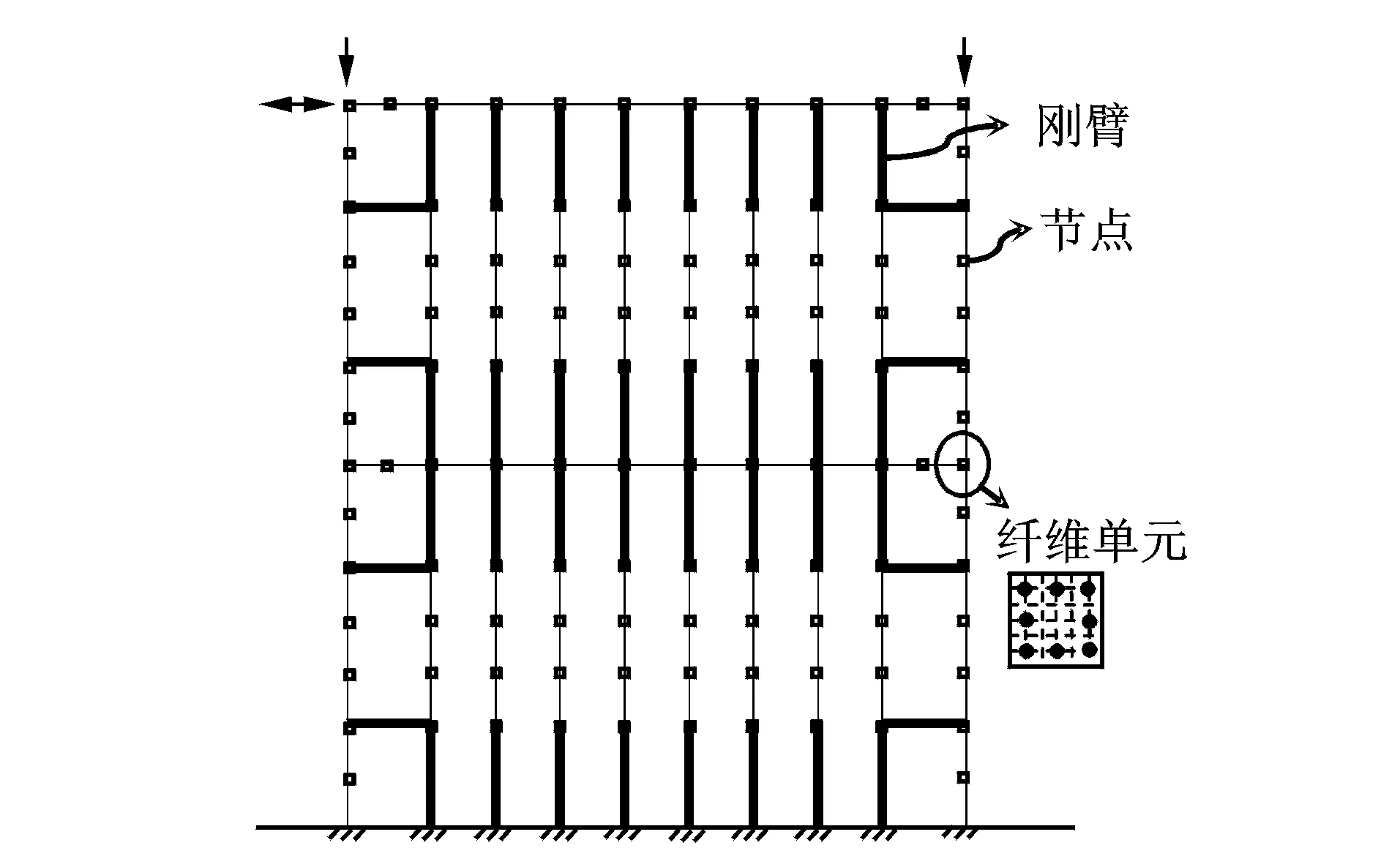
图3 RCFW结构的带刚臂纤维截面模型Fig.3 Fiber section model with rigid element for RCFW structure

如图3所示，建立了RCFW结构的带刚臂纤维截面模型。其中，梁柱构件采用纤维梁单元模拟；加载过程中，由于预制竖缝的存在，内填墙被分割成若干并联的小墙段，各缝间小墙段的变形类似于短柱，初期以弯剪变形为主；随着预制竖缝的延伸和贯通，墙肢高宽比增大，以弯曲变形为主，因此采用考虑剪切变形的纤维梁单元来模拟缝间墙段，在ABAQUS中选用三维二阶Timoshenko梁单元B32，通过*rebar关键字定义钢筋纤维，每插入一根钢筋纤维即在混凝土截面上增加一个材料积分点。此外，对于内填墙和框架之间的刚性抗剪连接件以及实体墙部分，由于刚度很大，在模型中简化为刚臂处理。

表1 材料力学参数

1.2 纤维截面的本构关系

纤维梁单元最初由Taucer[7]等提出，将杆件截面划分为若干纤维，如图4所示，每个纤维均为一维受力，不同的纤维可以定义不同的材料单轴本构，从而适用于任意截面特性的构件，如钢筋混凝土、型钢混凝土、钢管混凝土、预应力混凝土构件等，能直接反映钢筋混凝土或钢-混凝土组合构件在往复荷载作用下压、弯、剪、扭耦合引起的截面的本构关系，在保证计算效率的同时获得较高的求解精度[8-10]。

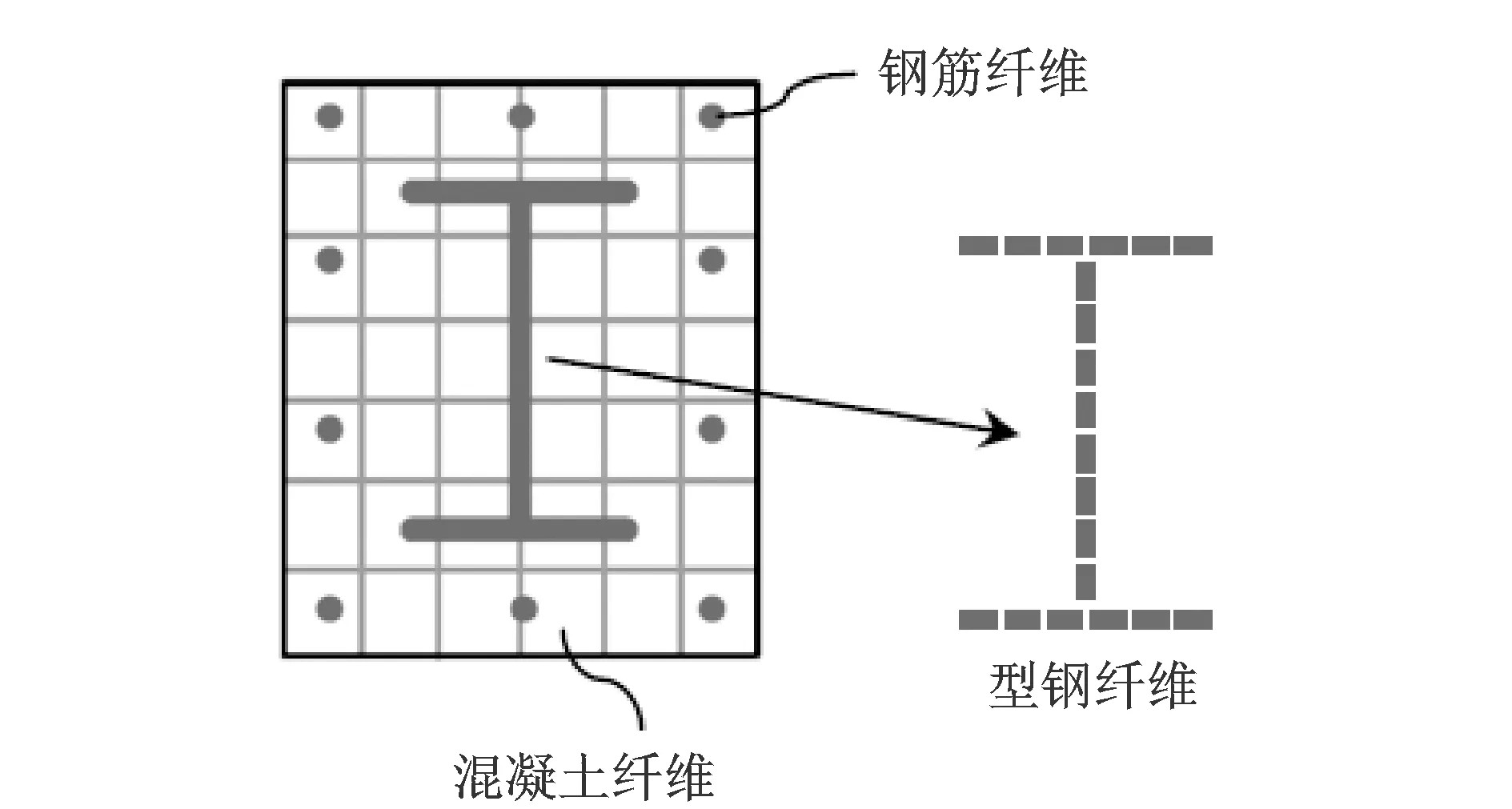
图4 纤维组合截面Fig.4 Fiber composite sections

1个梁单元的截面上有6个内力分量，包括轴力N、两个方向的剪力Vx和Vy、两个方向的弯矩Mx和My以及扭矩T，这6个内力分量可写成截面广义应力张量的Voigt形式列矩阵F={N,Vx,Vy,Mx,My,T}T；相应的截面广义应变张量的Voigt形式列矩阵可写为Δ={ε,γx,γy,φx,φy,w}T，其中ε为轴向应变,γx和γy为两个方向的剪应变,φx和φy为两个方向的曲率,w为扭转角。截面的本构关系是要寻求F和Δ之间的关系。

考虑到剪扭弹塑性对弯曲变形为主的构件的非线性反应的贡献较小，因此假定对于剪扭分量，即{Vx,Vy,T}T和{γx,γy,w}T之间满足线弹性关系；同时假定剪切分量和压弯分量之间不耦合，可定义{Vx,Vy,T}T和{γx,γy,w}T之间的刚度矩阵为K1，对于纤维组合截面，K1可由下式表达

(1)

式中G0i为第i个纤维的初始剪切模量；E0i为第i个纤维的初始弹性模量；k为截面剪切校正因子，对于矩形截面可取k= 1.2；Ai为第i个纤维的面积；xi和yi分别为第i个纤维中心点在截面局部坐标系中的坐标；n为截面的纤维总数。

而对于压弯分量，即{N,Mx,My}T和{ε,φx,φy}T之间为非线性关系，定义F2={N,Mx,My}T，Δ2={ε,φx,φy}T，F2和Δ2之间的截面切线刚度矩阵为τK2，τK2可通过纤维截面上各纤维的材料单轴本构关系积分得到。

假定仅压弯分量时，纤维截面始终保持平面且和构件的纵轴垂直，可得到截面纤维轴向应变ε和截面广义应变压弯分量Δ2之间，以及对应增量δε和δΔ2之间满足如下关系：

ε=LΔ2

(2)

δε=LδΔ2

(3)

式中L为变形协调矩阵，可由下式表达

(4)

根据式(2)和(3)求得的纤维轴向应变ε和应变增量δε，通过材料单轴本构关系，即可求得截面的纤维轴向应力σ和纤维轴向切线模量矩阵τE。其中，τE= diag{Et1,…,Eti,…,Etn}，Eti为第i个纤维的轴向切线模量。由虚功原理[8]和式(2)及(3)的变形协调条件，可得如下方程

(5)

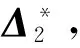
δF2=LT(τEA)LδΔ2

(6)

由截面切线刚度矩阵的定义，可得压弯分量的截面切线刚度τK2的表达式

τK2= LT(τEA)L

(7)

将K1和τK2集成即可得到截面的切线刚度矩阵τKsec。由于假定剪切分量和压弯分量之间不耦合，截面的本构关系，即F-Δ关系也可分开表达为

(8)

2 材料单轴本构模型的开发

2.1 混凝土单轴滞回本构关系

由于地震作用的随机性和复杂性，混凝土可能会从骨架曲线卸载后经历多次往复加卸载，再次回到骨架曲线时的应变可能会被大大推迟，甚至无法再回到骨架曲线。因此，本文在只考虑与历史最大应变相关的混凝土损伤的Yassin[11]滞回本构模型的基础上，提出了可以考虑累积损伤效应的混凝土滞回本构模型，如图5所示。该模型可准确地考虑复杂加-卸载历史下混凝土材料的强度退化和刚度退化等特性，同时在保证计算精度的前提下，滞回准则尽量简化，由一组折线来描述，保证了较高的计算效率。

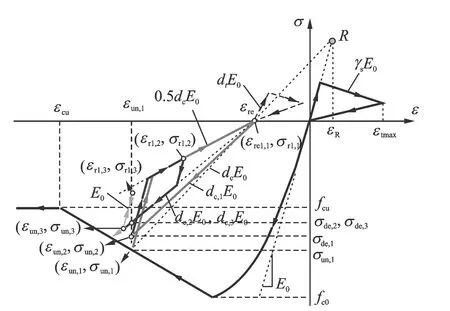
图5 混凝土单轴滞回本构模型Fig.5 Uniaxial constitutive model of concrete

模型的骨架曲线采用修正的Kent-Park模型[12]，受拉段采用带有软化段的二折线骨架线；受压段采用三段式骨架线，由下式定义

(9)

通过一个虚拟点R控制卸载与再加载刚度的退化。R的位置由损伤参数dcu决定。R点对应的应变εR按下式计算

(10)

对应的应力为E0εR。dcu的取值范围如下式

(11)

式中fcu为混凝土极限压应变εcu对应的强度，εc0为混凝土轴心抗压强度fc0对应的应变。E0为初始弹性模量，E0= 2fc0/εc0。

首先讨论受压段的滞回准则，R点确定后，记混凝土从骨架曲线上某次卸载起点的应力和应变分别为σun,1和εun,1，从该点开始，到回到骨架曲线之前，第i次卸载点处的应力和应变分别记为σun,i和εun,i，以图5为例，i= 1～3。连接卸载起点(εun,1，σun,1)与R点，连线的斜率记为dcE0，其中dc为与历史最大压应变相关的受压损伤系数，连线与应变轴的交点即为残余应变εre。假定混凝土每次从骨架曲线卸载至回到骨架曲线之前的残余应变εre保持不变，仅由(εun,1，σun,1)与R点决定。卸载准则为：先按初始刚度E0卸载，当卸载至与经过残余应变点(εre，0)且刚度为0.5dcE0的直线相交时，改为按0.5dcE0的卸载刚度卸载直至与应变轴相交于εre。再加载准则分为反向再加载和同向再加载两种情况，定义第i次受压再加载点处的应力和应变分别为σrl,i和εrl,i，由图5可知，εre≤εrl,i≤εun,i，0≤σrl,i≤σun,i。定义第i次受压再加载应变回到εun,1时发生强度退化后的更新应力为σde,i，对于未进行再加载的初始状态，σde,0=σun,1，第i次(i≥ 1)再加载的更新应力σde,i可按下式计算

(12)

式中 ηd为循环软化系数，对于一般钢筋混凝土构件，建议可取0.92。

连接(εre，0)点和(εun,1，σde,i)点，连线的斜率记为dc,iE0，其中dc,i为考虑累积损伤效应的受压损伤系数。如图5所示，反向再加载时，混凝土从(εre，0)点开始按损伤刚度dc,iE0加载直至返回骨架曲线；同向再加载时，先按初始刚度E0加载，达到(εre，0)点与(εun,1，σde,i)点连线时改为按损伤刚度dc,iE0加载直至返回骨架曲线。

对于受拉段，卸载准则为一条指向原点或上一次的残余应变点(εre，0)的直线。反向再加载时，通过式(13)定义的受拉损伤系数dt控制再加载刚度以及抗拉强度的退化，dt与历史最大拉应变相关，如图5所示，发生损伤后，再加载刚度退化为dtE0，抗拉强度相应地退化为dtft，受拉软化模量保持不变；同向再加载时，则直接沿原卸载路径返回至骨架曲线

(13)

式中γs为受拉骨架线下降段软化模量与E0的比值，一般可取0.1；εt0=ft/E0，为混凝土开裂应变；εtmax为历史上经历的最大拉应变。

2.2 钢筋单轴滞回本构关系

钢筋材料的骨架曲线采用带有硬化段的双折线，硬化模量Es=αE0。对于材料的滞回准则，其中的卸载行为较为简单，按初始弹性模量E0卸载；而反向再加载行为考虑了刚度退化和滞回捏拢行为，在历史最大应变指向型的Clough刚度退化准则[13]的基础上，引入过渡点来反映钢筋-混凝土界面之间的黏结-滑移产生的捏拢效应[14]，反向再加载路径由一根先指向过渡点再指向历史最大应变点的双折线来描述。过渡点的坐标由κd和κf两个参数控制，过渡点的横坐标为(1-κd)εre，其中εre为该加载方向的历史最大残余应变，κd控制过渡点的横坐标；反向加载起点与过渡点的连线的延长线指向(εm，κfσm)，其中εm和σm分别为该方向的历史最大应变及其在骨架曲线上对应的应力强度，κf控制过渡点的纵坐标；若该方向未曾屈服过，则取εre= 0，εm=εy，σm=fy。在数值分析中，为兼顾收敛性，建议κf取0.7～1.0，当κf= 1.0时，即不在钢筋本构模型中考虑捏拢效应，图6模型退化为Clough[13]模型。

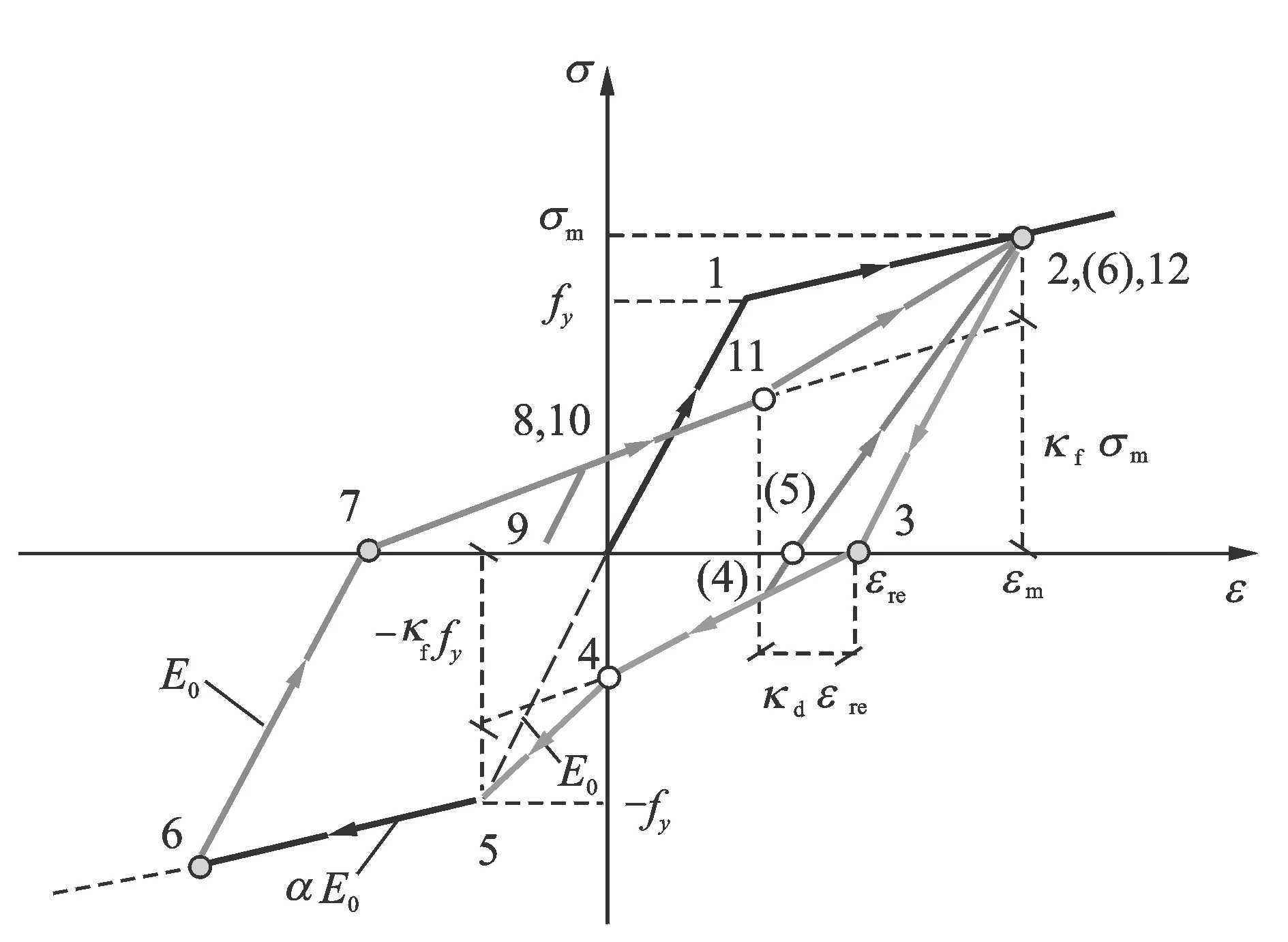
图6 钢筋单轴滞回本构模型Fig.6 Uniaxial constitutive model of steel reinforcement

如图6所示，反向再加载路径先指向过渡点(7→11)，然后指向加载方向的历史峰值应变点(11→12)；若该方向未屈服则先指向过渡点再指向屈服点(3→4→5)。若卸载中途发生同向再加载，则直接按初始刚度E0加载返回卸载点，然后继续沿原加载路径前进(8→9→10→11)。如果反向再加载路径与横坐标轴的交点已经超过过渡点横坐标，则再加载路径直接指向历史峰值应变点((4)→(5)→(6))。

2.3 基于ABAQUS平台的程序开发及流程

以ABAQUS的隐式模块ABAQUS/Standard为计算分析平台，基于用户子程序接口UMAT[15]开发了上述混凝土和钢筋单轴滞回本构模型，可用于钢筋混凝土结构弹塑性动力反应分析时定义杆系单元的材料本构，较为准确地模拟钢筋-混凝土组合截面的拉弯或压弯非线性行为。

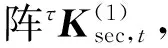
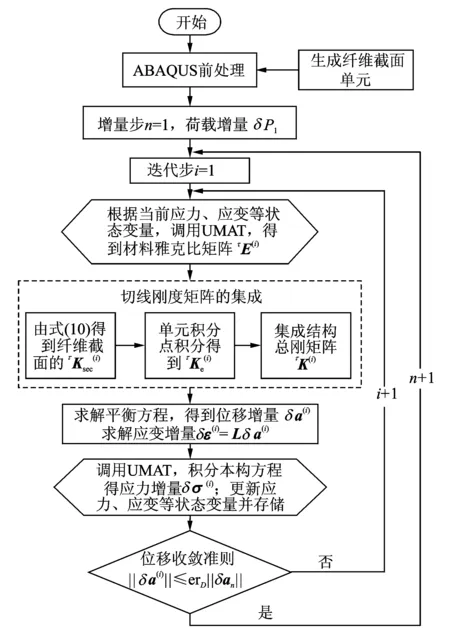
图7 程序流程及UMAT调用关系Fig.7 Program flow and call relationships of the UMA

3 试验验证与对比分析

3.1 试验结果及模型验证

试验水平加载方案采用荷载-位移混合控制的方法。初始水平加载采用荷载控制，每级50 kN，每级循环1次，荷载递增直至试件屈服。屈服后改为位移控制加载，以试件屈服位移Δy0的倍数作为位移加载增量，每级循环3次。当荷载低于峰值荷载的85%或试件变形太大不适于继续加载时停止试验。采用图3所示的RCFW结构的带刚臂纤维截面模型，结合本文开发的考虑损伤的混凝土单轴本构模型和考虑刚度退化及捏拢行为的钢筋单轴本构模型的UMAT子程序，模拟了RCFW试件往复加载的全过程。计算模型的加载制度及边界约束条件与试验一致，同时考虑几何非线性和材料非线性，采用BFGS二阶准Newton法求解非线性方程组。

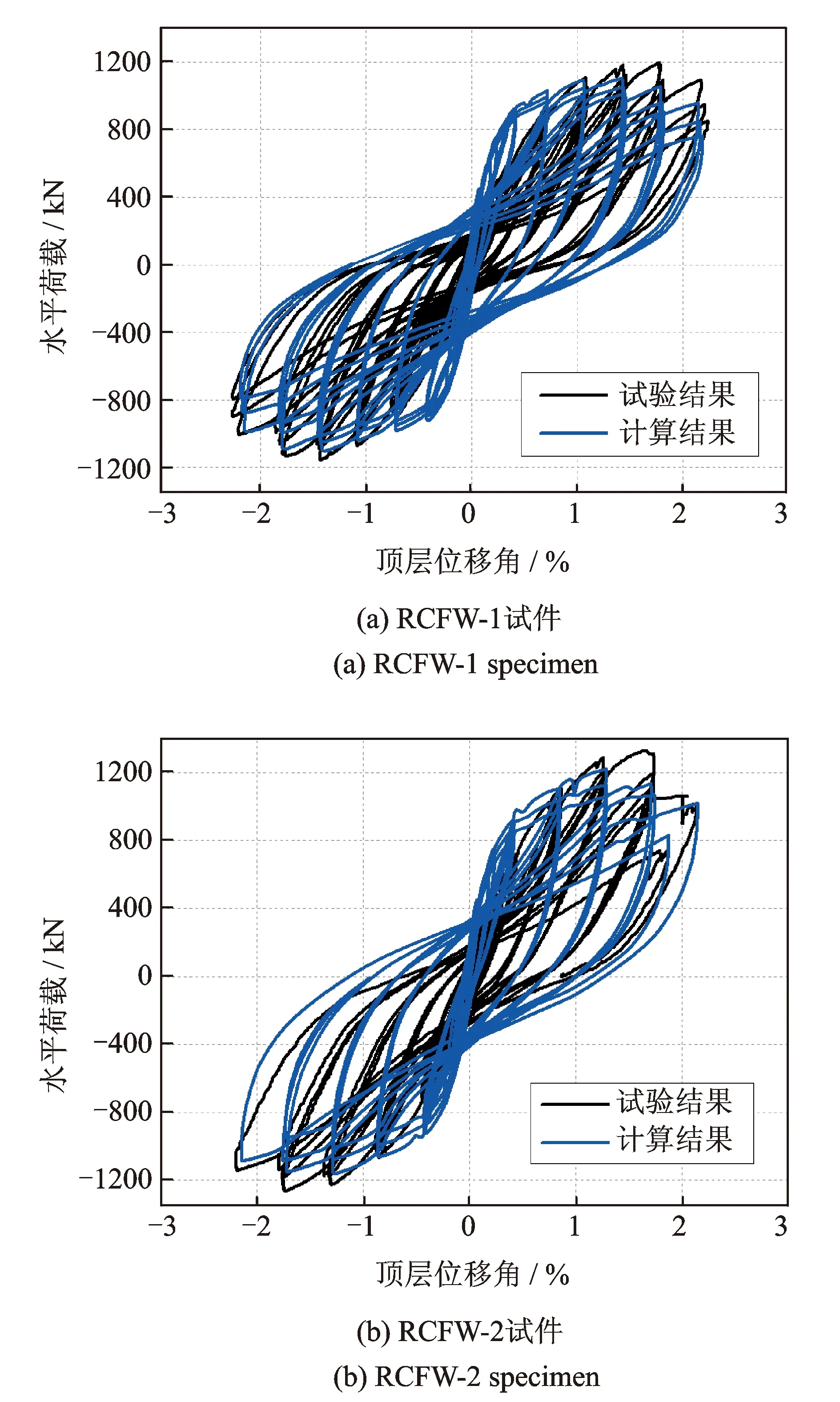
图8 试验滞回曲线和模型计算曲线的比较Fig.8 Comparison between test and calculated hysteretic curves

试件RCFW-1和RCFW-2的水平荷载-顶层位移滞回曲线和本文模型计算结果的对比分别如图8(a)和(b)所示。由图可见，计算模型可较为真实地模拟RCFW结构在反复加载过程中的承载力、刚度退化及捏拢现象。值得注意的是，图3所示的计算模型中框架梁柱及缝间墙段分别与刚臂单元共节点刚接，未另设弹簧单元来考虑钢板连接件与混凝土界面间的相对滑移；同时，纤维截面单元中各纤维之间满足式(4)的变形协调矩阵L，即假定各纤维之间黏合在一起，不存在相对滑移。但由于各纤维的材料本构采用了本文所开发的UMAT材料模型，直接通过材料层次的强度、刚度退化和捏拢行为来考虑构件层次的恢复力特性，因此得到了与试验结果吻合良好的模拟滞回曲线。

计算曲线的初始抗侧刚度相比于试验结果偏大，主要是由于初始弹性阶段计算模型中未考虑结构的初始缺陷及混凝土材料的微裂缝等引起的刚度损失。试件RCFW-1和RCFW-2的峰值承载力Pmax和极限位移角θu的试验值与计算值的对比列于表2，其中θu取试件承载力下降到0.85Pmax时对应的位移；计算得到的Pmax和θu与试验结果的误差分别在9%和8%以内。

表2 承载力及位移试验值与计算值的对比

Tab.2 Comparison between test and calculated characteristic values

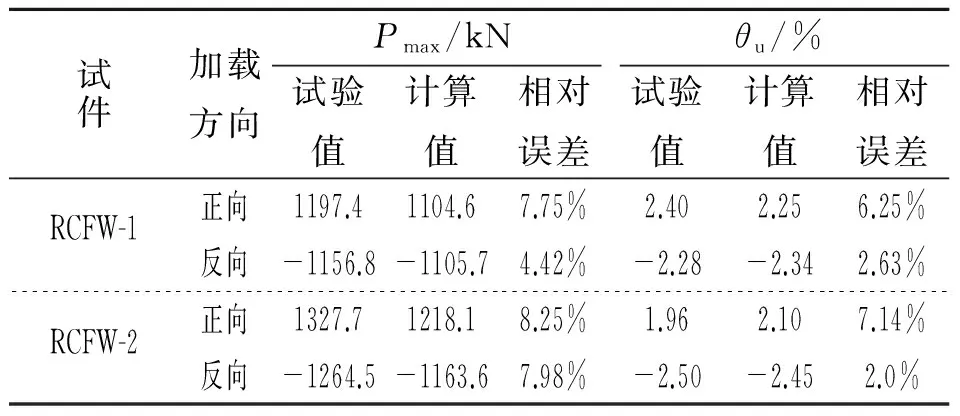
试件加载方向Pmax/kNθu/%试验值计算值相对误差试验值计算值相对误差RCFW-1正向1197.41104.67.75%2.402.256.25%反向-1156.8-1105.74.42%-2.28-2.342.63%RCFW-2正向1327.71218.18.25%1.962.107.14% 反向-1264.5-1163.67.98%-2.50-2.452.0%

3.2 不同本构模型对比

图9为不同滞回本构模型对计算结果的影响。由于图3所示的带刚臂纤维截面模型中将钢板连接件近似作为刚臂处理，因此计算模型只涉及混凝土和钢筋两种材料本构。通过一种材料的滞回本构模型不变而仅改变另一种材料的滞回本构模型，分别考察了混凝土、钢筋材料选取不同本构模型时对计算结果的影响。为方便比较，计算模型的竖向轴压比取0.3，水平加载制度改为1Δy0→2Δy0…→nΔy0…，即以试件屈服位移Δy0的倍数作为每一循环的位移加载增量，每级循环1次。

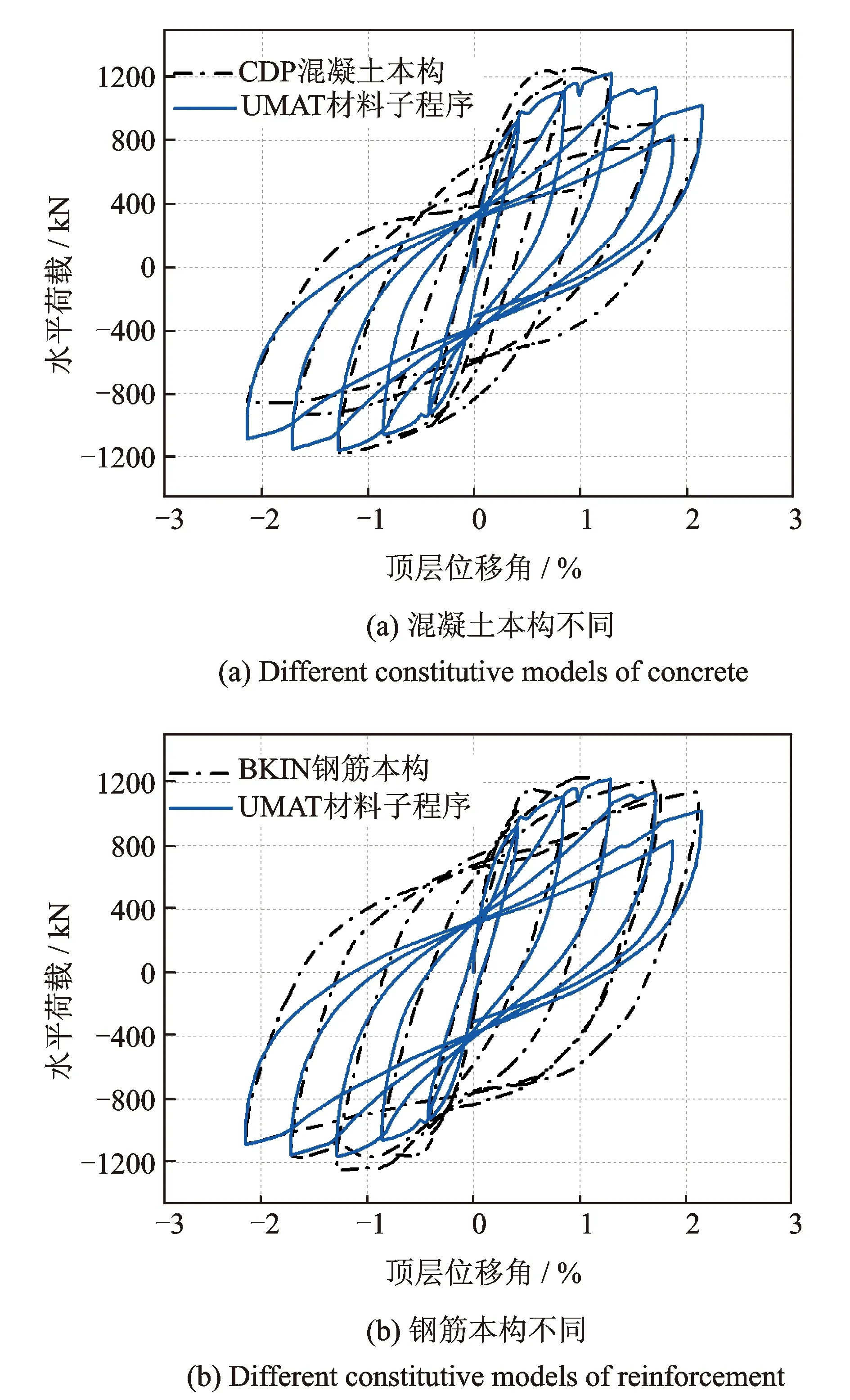
图9 不同滞回本构模型对计算结果的影响Fig.9 Influence of different constitutive models on simulation results

图9(a)为采用不同混凝土材料本构计算得到的RCFW试件的滞回曲线，其中钢筋材料都采用本文开发的UMAT材料子程序，混凝土材料分别采用ABAQUS程序自带的塑性损伤 (Concrete Damaged Plasticity, 简称CDP) 多轴本构模型和本文开发的UMAT材料子程序。其中，CDP模型是目前几种常用的通用有限元软件，如MSC.MARC，ABAQUS，ANSYS等中唯一能考虑混凝土在往复加载中的损伤累积等特征的本构模型，适用于模拟往复或地震作用下混凝土结构行为。该模型采用非关联流动、多重硬化的修正Lubliner屈服面[15]，其屈服面函数如下式所示

(14)

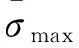
(15)

其余参数的计算公式如下式:

(16)

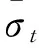
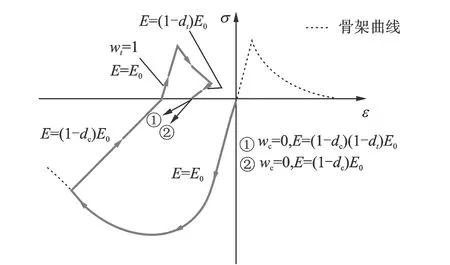
图10 CDP模型的单轴滞回准则Fig.10 CDP model under uniaxial cyclic conditions

CDP模型的卸载及再加载准则采用Lee提出的多重损伤因子理论[16]，混凝土进入塑性后，通过两个独立的损伤因子dc和dt来考虑损伤引起的初始弹性刚度阵的折减，如图10所示。d=0表示无损伤，卸载刚度与初始弹性刚度相等；d=1表示完全损伤，卸载刚度为零。目前国内外学者提出了各种损伤模型，用于损伤因子的标定，根据不同损伤模型计算出的损伤因子随混凝土应变的变化规律差异较大，在分析中需对损伤因子进行大量的试算调整才能得到较为理想的结果。反向再加载时，还可通过刚度恢复系数wc或wt来模拟裂缝闭合引起的弹性刚度恢复，w=0表示反向加载时刚度不恢复，w=1表示反向加载时刚度完全恢复。本文取受压刚度恢复系数wc=0.05，受拉刚度恢复系数wt=0，但得到的模拟曲线在拉-压状态转换阶段的再加载刚度仍比采用自开发的UMAT本构得到的模拟结果大，说明CDP模型低估了钢筋-混凝土界面间的滑移捏拢效应，未能真实地反映混凝土的裂缝闭合行为。

图9(b)为采用不同钢筋材料本构计算得到的RCFW试件的滞回曲线，其中混凝土材料统一采用本文开发的UMAT材料子程序，钢筋材料分别采用简单的双线性随动硬化(Bilinear Kinematic Hardening，简称BKIN)本构模型和本文开发的UMAT材料子程序。由图9(b)可知，钢筋滞回准则对模拟曲线的滞回环形状也存在很大影响。当采用BKIN模型时，得到的滞回曲线明显偏于饱满，其原因主要是该简化模型在很大程度上弱化了钢材在往复荷载作用下的Bauschinger效应，且没有计入构件层次的黏结-滑移效应和混凝土保护层剥落等引起的刚度退化和捏拢效应，因此高估了结构在循环作用下的再加载刚度以及耗能能力，使分析结果偏于不安全。

3.3 不同有限元模型对比

按试件的实际尺寸建立了RCFW结构的精细化实体模型，如图11所示，实体模型采用分离式钢筋建模，混凝土部分采用实体单元C3D8R，钢筋部分采用桁架单元T3D2，利用ABAQUS提供的embed约束将钢筋单元“嵌入”混凝土单元，实现两者的自由度耦合，钢筋单元的节点平动自由度作为从自由度，由周边混凝土单元的节点主自由度通过插值得到。另外，采用壳单元S4R来模拟由预埋钢板和高强螺栓组成的刚性抗剪连接件，连接件两端采用embed约束“嵌入”混凝土单元。

图11 RCFW结构精细化实体模型Fig.11 Detailed solid model of RCFW system

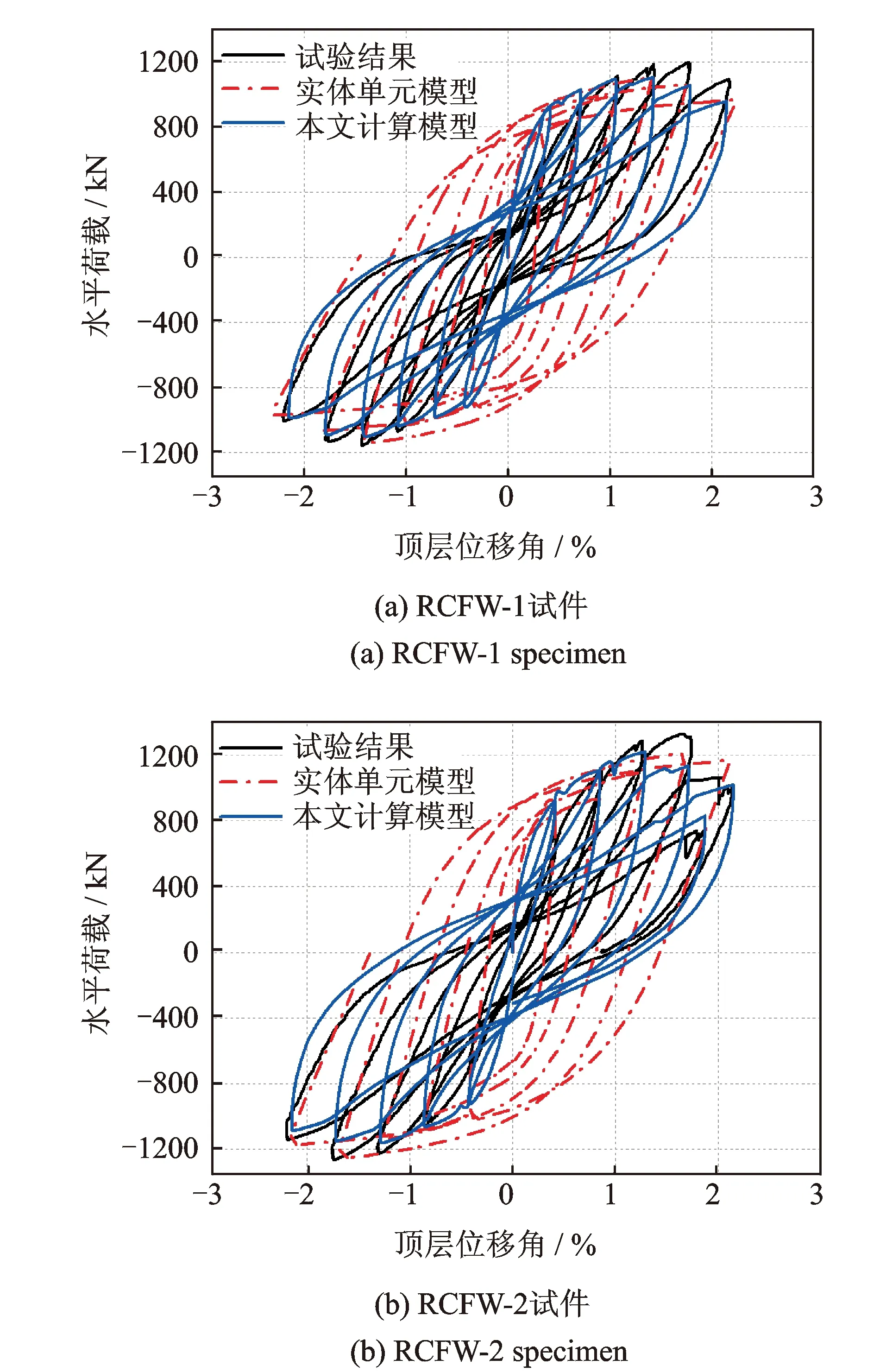
图12 不同计算模型的模拟滞回曲线对比Fig.12 Comparison of simulated hysteretic curves between different models

实体模型中混凝土材料采用CDP本构；钢板采用Chaboche非线性混合硬化本构，按文献[17]的Q345B结构钢材性滞回试验的结果进行标定；钢筋采用本文开发的钢筋UMAT本构。计算得到的水平荷载-顶层位移滞回曲线如图12所示，由图可见，实体模型的计算滞回曲线过于丰满，钢筋本构对实体模型的计算结果影响较小，无法模拟试验曲线的捏拢现象。此外，相同条件下，实体模型的计算耗时(8.5 h)约为带刚臂纤维截面模型计算机时(65 s)的470倍。

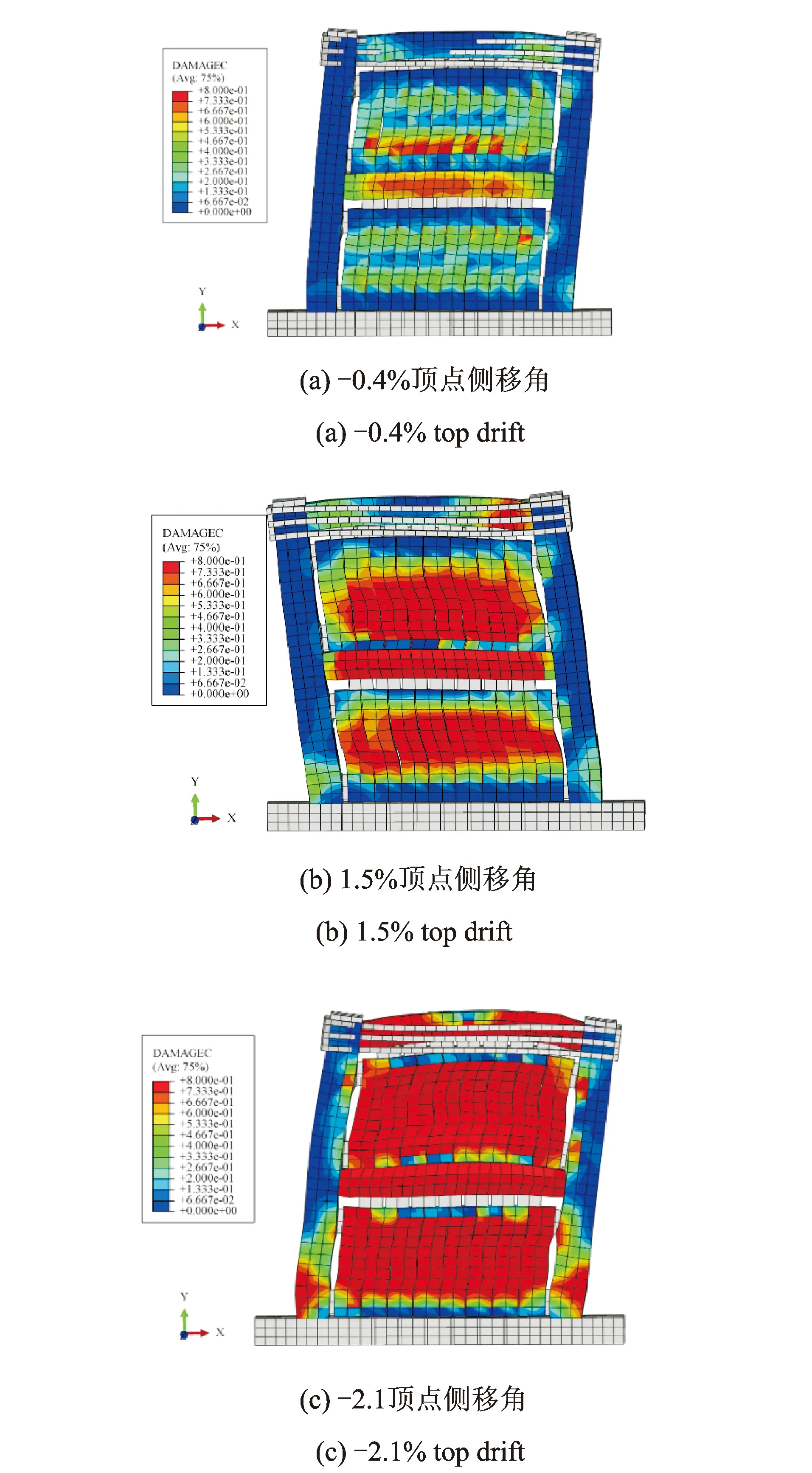
图13 往复荷载作用下RCFW试件的损伤演化Fig.13 Damage process of the RCFW specimen under cyclic loading

基于实体模型计算得到的RCFW试件在往复荷载作用下混凝土的受压损伤演化规律和试件变形模式与试验结果吻合较好，如图13所示，试件进入非弹性阶段后，由于预制竖缝的存在，内填墙主要以弯曲变形为主；当顶层位移角达到0.4%时，试件进入非弹性阶段，如图13(a)所示，损伤主要集中在缝间墙段，竖缝剪力墙作为抗震第一道防线率先进入耗能。当顶层位移角达到1.5%时，试件达到其峰值承载力，如图13(b)所示，内填墙和底梁的混凝土损伤严重，顶梁梁端也开始出现损伤集中区，但柱端基本保持完好，满足“强柱弱梁”的设计要求。进一步加载，当顶层位移角达到2.1%时，如图13(c)所示，柱脚和内填墙四角都开始出现损伤集中区，试件整体进入破坏阶段。

4 结 论

(1) 地震作用下，带竖缝剪力墙以弯曲变形为主，使RCFW结构整体具有良好的延性；同时预制竖缝阻碍了斜裂缝的发展和贯通，墙体产生大量分布微裂缝，提高了结构的整体耗能能力。

(2) 纤维截面单元相比于实体单元能更好地描述弯曲变形为主的钢筋-混凝土复合截面构件的力学行为。本文针对RCFW结构所提出的带刚臂纤维截面模型建模工作量小，计算精度、效率高，适用于实际工程中整体结构的弹塑性动力分析。

(3) 基于ABAQUS用户子程序接口UMAT，开发了一组混凝土和钢筋单轴滞回本构模型，可用于纤维杆系单元，直接从材料层次考虑构件层次的刚度退化和黏结-滑移等行为，较好地模拟钢筋-混凝土复合截面在往复荷载作用下复杂的截面广义应力-应变关系。

(4) 通过对比不同材料本构对计算结果的影响可知，模拟曲线的承载力退化及卸载刚度退化受混凝土材料本构的影响较大，再加载刚度受钢筋材料本构的影响较大。

[1] 叶列平, 康胜, 曾勇. 双功能带缝剪力墙的弹性受力性能分析[J]. 清华大学学报(自然科学版),1999, 39(12):79—81.

Ye Lieping, Kang Sheng, Zeng Yong. Analysis of elastic behaviors for dual function slitted shear wall [J]. J. Tsinghua Univ. (Sci. &Tech.), 1999, 39 (12):79—81.

[2] 叶列平, 曾勇. 双功能带缝剪力墙的弹塑性地震动力反应分析[J]. 工程力学, 2002, 19(3): 74—77.

Ye Lieping, Zeng Yong. Elasto-plastic dynamic analysis of dual functional shear wall with built-in slits [J]. Engineering Mechanics, 2002, 19(3): 74—77.

[3] Eto H, Takeda T. Elastoplastic earthquake response analysis of reinforced concrete frame structures [C]. Report, Annual Meeting, Architectural Institute of Japan, 1973：1261—1262.

[4] 米旭峰. 带竖缝钢筋混凝土剪力墙的壁式框架分析模型[J]. 工程力学, 2010,27(1):188—194.

Mi Xufeng. Wall-column frame model of RC slit wall [J]. Engineering Mechanics, 2010, 27(1):188—194.

[5] Rassati G A, Hajjar J F, Schultz A E, et al. Cyclic analysis of PR steel frames with composite reinforced concrete infill walls[C]. In: Proceedings of advances in structures: steel, composite and aluminum (ASSCA)’03. Association for International Cooperation and Research in Steel-Concrete Composite Structures,Sydney Australia: 2003:1259—1265.

[6] JGJ 99-1998高层民用建筑钢结构技术规程[S]. 北京: 中国建筑工业出版社, 1998.

JGJ 99-1998 Technical specification for steel structure of tall buildings [S]. Beijing: China Architecture & Building Press, 1998.

[7] Taucer F, Spacone E, Filippou F C. A Fiber Beam-Column Element for Seismic Response Ana1ysis of Reinforced Concrete Structures [R]. Report EERC 91—17, Earthquake Engineering Research Center, University of California, Berkeley, 1991.

[8] Spacone E, Filippou F, Taucer F. Fiber beam-column modeling for non-linear analysis of R/C frames Part I, Part II [J]. Journal of Earthquake Engineering and Structural Dynamics, 1996, 25(7): 711—742.

[9] 聂建国, 陶慕轩. 采用纤维梁单元分析钢-混凝土组合结构地震反应的原理[J]. 建筑结构学报, 2011, 32(10): 1—10.

Nie Jianguo, Tao Muxuan. Theory of seismic response analysis of steel-concrete compositestructures using fiber beam elements [J]. Journal of Building Structures, 2011, 32 (10) : 1—10.

[10]陶慕轩, 聂建国. 材料单轴滞回准则对组合构件非线性分析的影响[J]. 建筑结构学报, 2014, 35(3): 24—32.

Tao Muxuan, Nie Jianguo. Influence of material uniaxial hysteretic laws on nonlinear analysis of composite structural members [J]. Journal of Building Structures, 2014, 35(3): 24—32.

[11]Yassin M H M. Nonlinear analysis of prestressed concrete structures under monotonic and cyclic loads [D]. University of California, Berkeley, California, U S, 1994.

[12]Kent D C, Park R. Flexural members with confined concrete [J]. Journal of the Structural Division, 1971, 97(7): 1969—1990.

[13]Clough R W, Johnston S B. Effect of stiffness degradation on earthquake ductility requirements[C]. Proceedings of Japan Earthquake Engineering Symposium, Tokyo,Japan,1966:195—198.

[14] Ibarra L F, Medina R A, Krawinkler H. Hysteretic models that incorporate strength and stiffness deterioration [J]. Earthquake Engineering and Structural Dynamics, 2005, 34(12): 1489—1511.

[15]ABAQUS. Analysis User’s Manual Volume I_V. Version 6.12 [M]. USA: ABAQUS, Inc., Dassault Systèmes; 2012.

[16]Lee J, Fenves G L. Plastic-damage model for cyclic loading of concrete structures [J]. Journal of Engineering Mechanics Division ASCE, 1998, 124(8): 892—900.

[17]戴国欣, 王飞, 施刚, 等. Q345与Q460 结构钢材单调和循环加载性能比较[J]. 工业建筑, 2012, 42(1): 13—17.

Dai Guoxin,Wang Fei, Shi Gang, et al. Comparison of monotonic and cyclic performances of structural steel Q345 and Q460 [J]. Industrial Construction, 2012, 42(1): 13—17.

Cyclic behavior and analytical model of RC frame with infill slit shear walls

XIAOKui1,2,ZHANGQi-lin2

(1. Shanghai Institute of Architectural Design & Research, Shanghai 200041, China;
2. College of Civil Engineering, Tongji University, Shanghai 200092, China)

Cyclic behavior of a structural system consisting of reinforced concrete frame with infill slit shear walls (RCFW) is studied in this paper. Pseudo-static tests were performed with two one-bay, two-story RCFW specimens built at one-half scale. A fiber section analytical model with rigid arm elements is proposed for this system to research the nonlinear structural behavior under cyclic loadings. Based on the user subroutine interface UMAT provided by the ABAQUS program, a set of uniaxial hysteresis constitutive models for concrete and steel reinforcement is developed, which can directly describe the resilience characteristics of a component from material constitutive models. It is proved correct and applicable of the proposed model through comparing with the experimental results of RCFW specimens under the cyclic loadings. the stiffness and strength degradation and pinch phenomenon can be well described in the calculated load-displacement curves of the RCFW structure under repeated loadings. Besides, the presented analytical model incorporating developed UMAT is efficient and numerically stable, which can be used for elastoplastic analysis of the RCFW structure and for assessment of seismic demand.

slit shear wall; cyclic; fiber section model; constitutive model; UMAT

2015-02-10；

2016-04-11

十二五国家科技支撑计划资助项目(2013BAJ10B10)；上海市科技人才计划资助项目(11XD1404900)

TU973.1+6

1004-4523(2016)06-1108-11

10.16385/j.cnki.issn.1004-4523.2016.06.021

肖魁 ( 1987— )，男，博士研究生。 E-mail: xiaokui87@126.com