马鞍屋盖表面分离泡流动形态研究①

叶继红， 孙虎跃

(东南大学混凝土结构及预应力混凝土结构教育部重点实验室， 江苏 南京 210018)

马鞍屋盖表面分离泡流动形态研究①

叶继红， 孙虎跃

(东南大学混凝土结构及预应力混凝土结构教育部重点实验室， 江苏 南京 210018)

利用粒子图像测速技术，通过风洞流场显示试验，给出了均匀流和格栅紊流两种工况下马鞍屋盖迎风高点和迎风低点处旋涡的截面形态特征以及时均、瞬时流线和涡量场分布，比较了两种工况下旋涡形态特征的异同，总结了来流在屋面上的速度分布规律。试验结果表明：当风向垂直于迎风前缘时，屋面迎风高点至迎风中点区域将出现典型的分离泡现象；而在迎风中点至低点区域，由于马鞍屋面为正向坡度，无法形成分离泡。均匀流场下分离泡再附长度近乎横跨整个屋盖；而湍流场中分离泡涡核离迎风前缘较近，且旋涡横截面积显著小于均匀流工况。结合风洞测压试验，分析了不同迎风高度处马鞍屋盖表面的脉动风压谱特性，明确了谱能量与旋涡运动或湍流尺度之间的演变关系。利用多个可视化平面的综合布置最终揭示出分离泡的三维形态特征，据此将马鞍屋盖划分为4个区域并提出合理的分区体型系数，为大跨马鞍屋盖抗风设计提供参考。

风荷载； 马鞍屋盖； 分离泡； PIV； 风压谱

引 言

大跨空间结构质量轻、柔性大、阻尼小等特点决定了其对风荷载非常敏感，同时其往往相对低矮，在大气边界层中处于风速梯度大、湍流度高的区域，再加上体型的个性化，其绕流和空气动力作用变得十分复杂。当来流垂直于大跨屋盖迎风前缘时，分离剪切层在屋盖表面再附形成旋涡，在此作用下，迎风前缘附近将形成强劲吸力，这使得该区域首先局部破坏，这也是引起屋盖最终破坏的元凶。因此，对屋面旋涡特性及其形成机制和演化规律的研究也是当前风工程领域中重点研究的内容之一。

粒子图像测速技术(PIV)是利用图像处理技术发展起来的一种流动测量技术，通过对流场图像的互相关分析获取流速信息，能够进行二维甚至三维流场测量，是一种非接触的、瞬态、全场流场测量的新技术。国内外研究人员对于旋涡的可视化试验研究主要针对二维平板和三维平屋盖结构。Saathoff等[1]利用流动显示试验结合风洞测压研究了不同湍流度和湍流尺度下二维钝体平板表面分离泡现象。结果表明：随着湍流度和湍流积分尺度的增大，分离泡的平均再附长度减小，相反迎风前缘的脉动风压将随之增大。Kim等[2]对三维矩形体表面分离泡结构及其周围的绕流情况进行了PIV试验，根据屋盖上方的平均速度分布确定了再附点的位置，量化马蹄涡区、迎风前缘区域和分离泡内部区域的湍流能量分布，发现湍流能量最大值位于屋盖迎风前缘附近的再循环区。Sarkar[3]对分离泡截面内的平均速度剖面进行了测量，发现在靠近迎风前缘的局部区域内，分离泡的正向流动与逆向流动的流速相当，随着与屋盖边界距离的增加，正向流动占主导，同时指出在分离泡作用区内，如果某点不再出现倒流，则可认为该点为分离泡再附点，即给出了定义分离泡边界的量化值。Brizzi[4]对二维平板模型和三维立方体模型进行了PIV试验和测压试验，给出了流场不同截面的涡量图和速度矢量图；讨论了不同雷诺数对于风压分布以及分离泡、马蹄涡结构特征长度的影响；分析了二维结构和三维结构上分离泡的异同，但并未对旋涡作用下的峰值吸力做深入研究。ShinjiIto[5]对一个立方体模型进行了同步的PIV试验和测压试验，发现分离泡结构在横风向较扁平，其还结合同步风压数据，给出了分离泡结构的再附点。国内同济大学李金国[6]等进行了TTU标准模型的风洞试验，采用PIV技术结合传统测压法，研究了TTU实测风压与试验风压的差异，给出了旋涡作用下的瞬时流迹图，但并未给出截面的速度矢量分布，且未对涡下峰值吸力做深入研究。东南大学叶继红教授课题组[7]进行了大跨屋盖刚性模型的PIV试验，给出了三维平屋盖和马鞍屋盖时均下旋涡形态及涡量场分布。

综上所述，关于分离泡结构的流场可视化试验研究对象大多限于平屋盖结构，得到结论是旋涡的时均化结果，它能够证实旋涡的存在性，却未能给出旋涡的量化流速、旋涡从形成发展至破裂的动态过程以及分离泡的三维形态特征。鉴于此，本文试验的研究对象为三维马鞍屋盖，来流有均匀流和格栅紊流两种工况，通过风洞PIV试验，给出了迎风高点、中点和低点处旋涡的截面形态特征以及时均、瞬时流线图和涡量场分布，分析了来流在屋面上的速度分布规律，比较了两种工况下旋涡形态特征的异同。利用测压试验给出了均匀流、格栅紊流下马鞍屋面不同迎风高度处的脉动风压谱，建立了谱能量与旋涡运动或湍流尺度之间演变关系。最后通过多个可视化平面的综合分析得到了旋涡的三维形态特征，进一步将马鞍屋盖划分为4个区域，并给出了对应区域的体型系数。

1 PIV试验装置与方案

马鞍屋盖刚性模型PIV试验在同济大学国家重点实验室TJ-4边界层风洞中完成。风洞的试验段由前、中、后三段洞体组成(总长5 m)，前段为可移动段，中、后段为固定段，中段试验段为模型置放区域，其尺寸为(宽×高×长)0.814 m×0.8 m×2.0 m。试验风速为0～30 m/s连续可调，试验区的流场<0.50%，满足试验流场要求。

本次试验模型为马鞍屋盖(矢跨比1/12和1/6)钝体结构模型，考虑到PIV试验中激光器片光尺寸(0.5 m×0.2 m)及风洞堵塞率的要求，将马鞍屋盖底面尺寸设定为0.21 m×0.21 m，低点高度分别为0.028和0.056 m，模型材料采用黑色有机玻璃。相机位于风洞的侧面，垂直拍摄光带内的流场，镜头的高度和风洞侧面中部位置持平，距地面约1.5 m。试验中平均风速为10 m/s。如图1所示，模拟风场有均匀流和等间距格栅湍流两种工况，湍流场下平均屋檐高度处的湍流度维持在10%。

PIV设备共分为5个部分，即激光器(YAG Laser)、同步仪(Synchronizer)、高速CMOS相机、计算机以及粒子投放设备。试验中相机工作频率为200 Hz，像素为2400×1800，全分辨率下相机的帧频为480 fps。PIV试验中的示踪粒子为一种油状液态物质，利用氮气通过压力控制器将液态示踪粒子喷射到风洞里形成雾气。由于马鞍屋盖存在迎风高点和低点，为了更全面地观察分离泡的截面流动特征及三维形态，试验设定5个可视化平面且可视化面与来流方向平行，如图2所示。

图1 两种风场试验Fig.1 Two kinds of wind field experiment scheme

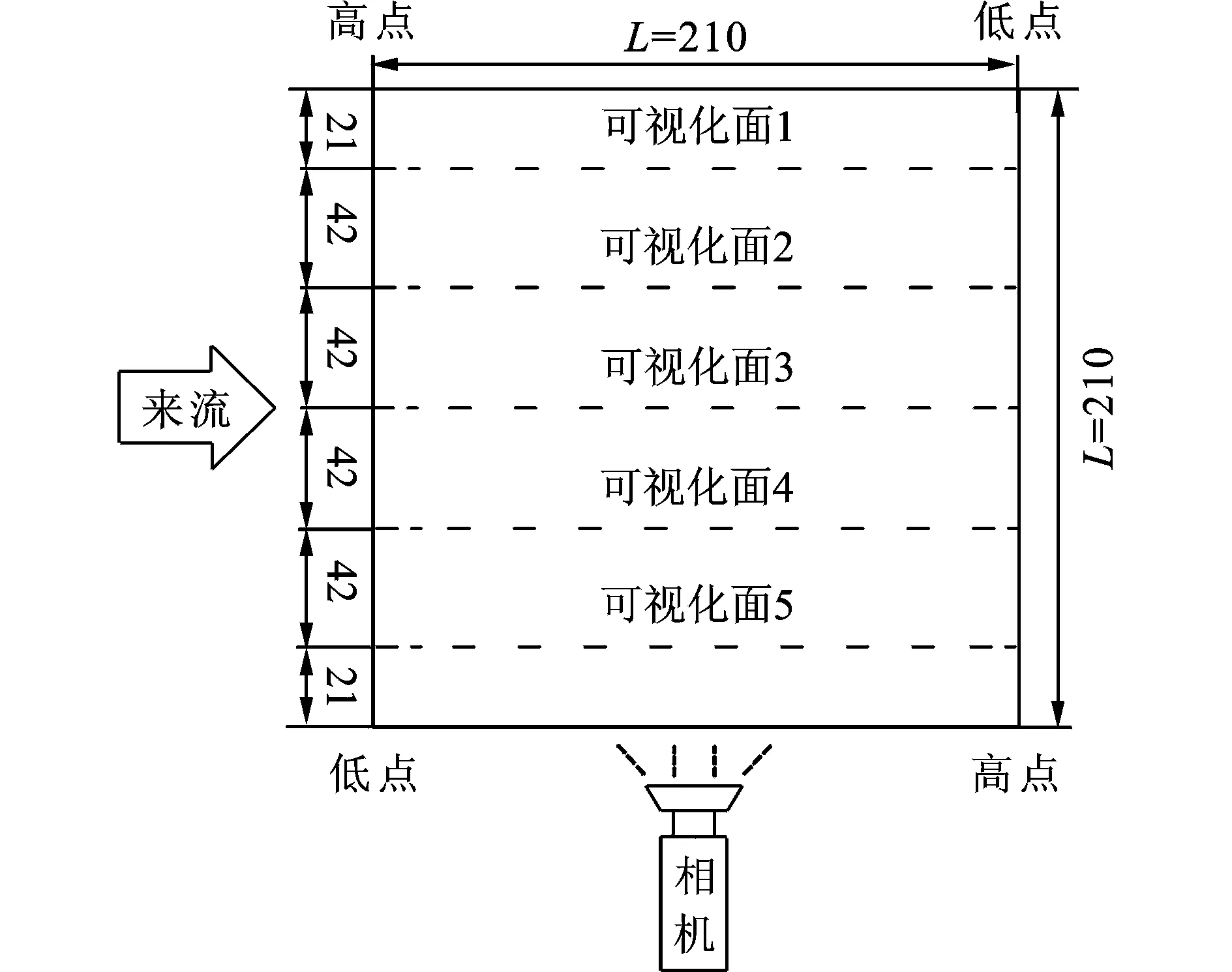
图2 可视化平面位置(单位：mm)Fig.2 Visual plane position (Unit: mm)

2 PIV试验结果分析

2.1 马鞍屋盖模型(矢跨比1/12，低点56 mm)试验结果分析

2.1.1 旋涡结构时均特征

当来流风垂直于马鞍屋盖迎风墙面时，气流将在迎风顶点处发生分离，分离的剪切层由于黏性效应会再附到屋面，形成不通气的空腔，通常称为分离泡，它使得靠近建筑物屋盖前缘产生极值负压。图3给出了均匀流和格栅紊流下可视化面1流线和涡量场。从图3(a)，(c)可以看出，分离泡的截面形状为椭圆形。来流为均匀流时，其各尺度湍流成分相对较少，导致沿着屋面附面层的倒流区较长，涡核高度较高。由图3(b)可知，来流未到达迎风高点时，由于受到屋盖的干扰作用，涡量已出现负值，说明此处已存在涡旋运动。在迎风前缘上方楔形区的涡量达到最大值，屋盖的表面将形成强劲的风吸力。在分离泡上方存在涡量极值狭长带，分离泡四周涡量均为负值，而其他区域涡量基本为零。随着来流向下游发展，旋涡逐渐脱落，负向涡量最终被空气黏性所耗散。与均匀流相比，格栅紊流下的分离泡紧贴马鞍屋面且靠近屋盖的迎风前缘。随着湍流度的增大，再附长度在不断减小，其原因是由于小尺度湍流成分在前缘分离卷吸成涡旋，而在均匀流场中各尺度的湍流成分缺少，再附长度较长。旋涡横截面积的减小直接导致涡量最大值和涡量极值狭长带长度的降低，但涡量峰值仍然出现在迎风顶点的上方(图3(d))。

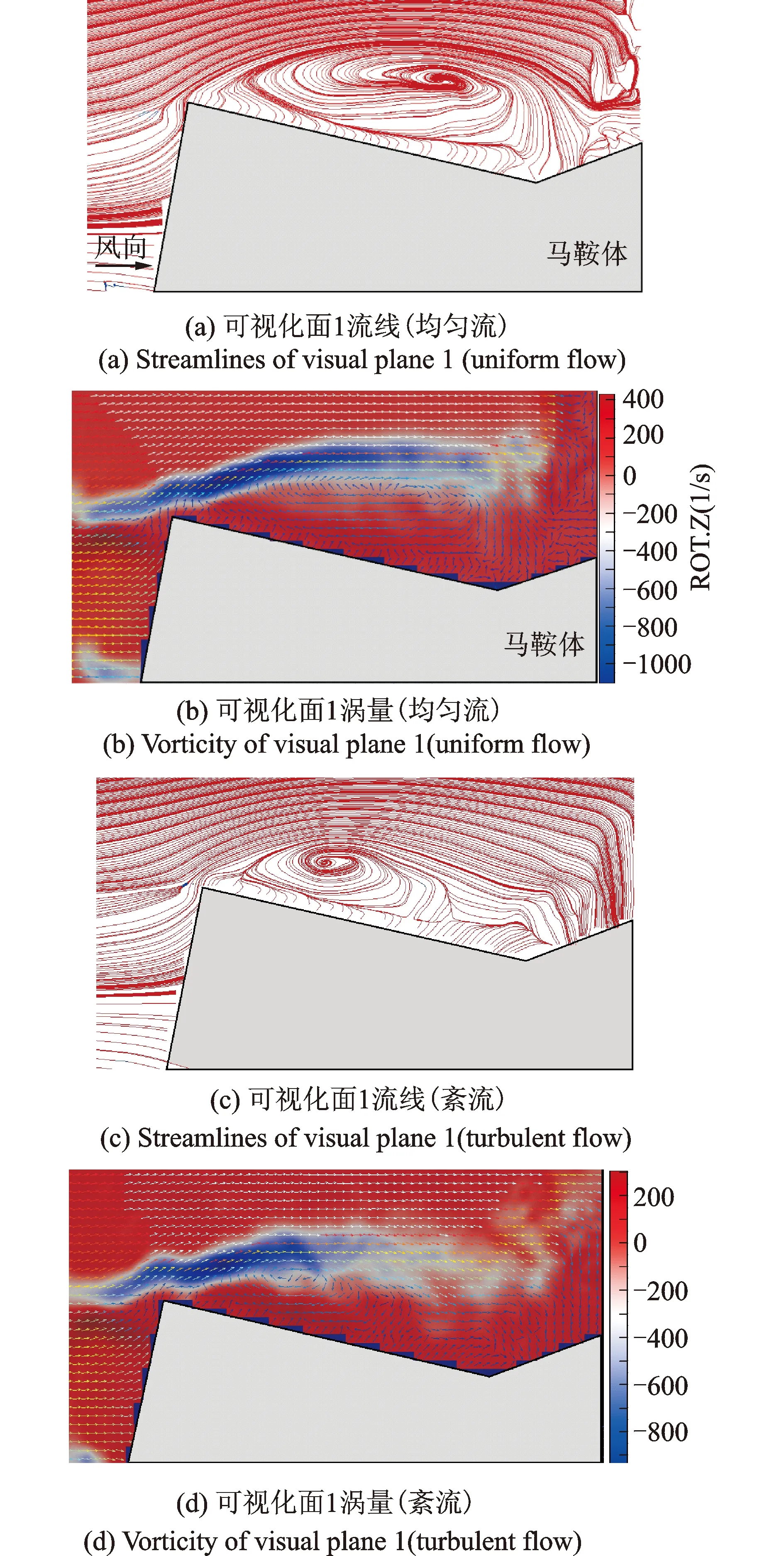
图3 可视化面1流线和涡量场Fig.3 Streamlines and vorticity field of plane 1

图4给出了两种来流工况下可视化面1速度矢量和速度竖直分布。如图4(a)，(c)所示，将屋面沿来流风向均分9等分，依次命名为截面0至截面9。以0-1截面区间为例，起始截面0上所有点的速度为0，终止截面1上所有点的速度为10 m/s，其间各点的速度可以根据起始、终止截面的速度和各点距起始截面的距离线性内插得到，其他各截面区间类推。图4(b)分析表明，来流到达迎风墙面时速度已经大幅度降低，部分气流随着墙面向上运动，在到达迎风高点处来流与倒流相遇，导致迎风前缘处沿高度方向速度梯度大。紧贴马鞍曲面的附面层速度几乎为零。在涡核截面7位置，从屋面至涡核位置段高度内，出现第一个速度拐点，即速度先增大后减小，而第二个速度拐点出现在涡核位置，涡核和再附点位置顺风向速度接近零值，最后风速继续增大至来流风速。相比于均匀流，紊流下的曲线拐点位置高度明显低于均匀流(图4(d))，这也是由于湍流度的增大使分离剪切层提前再附所致。可以看出，随着湍流度的增大，旋涡平均再附长度不断减小，而涡核离马鞍屋面的高度基本保持不变。

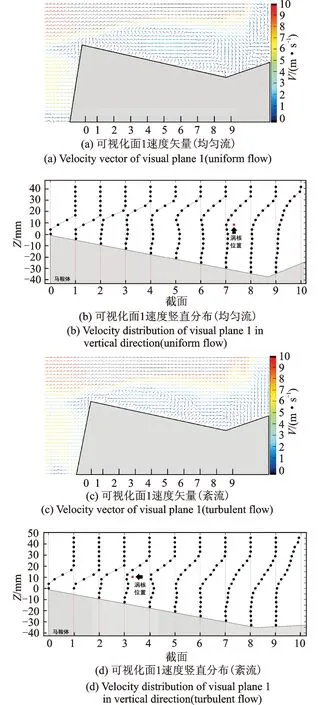
图4 可视化面1速度场分布Fig.4 Velocity distribution of plane 1

可视化面3流线和速度竖直分布如图5所示。与可视化面1内流线相比较，两种来流工况下面3处的旋涡更加扁平，旋涡影响范围均有所减小。马鞍曲率较小使得分离泡下方的流线近乎水平直线，在涡流的上部流线分布均匀。面3处紊流下的涡核离迎风前缘距离也是明显小于均匀流。由图5(b)，5(d)可知，迎风前缘处梯度风高度(速度从附面层0增大至来流风速10 m/s此段高度)较可视化面1均有明显增大，主要原因是由于屋面比较平坦，倒流与来流的碰撞断面增大。屋面上方的流速表现为S形增长模式直至来流风速，而尾流区的速度则增长缓慢，整个流域梯度风高度成线性增长趋势。

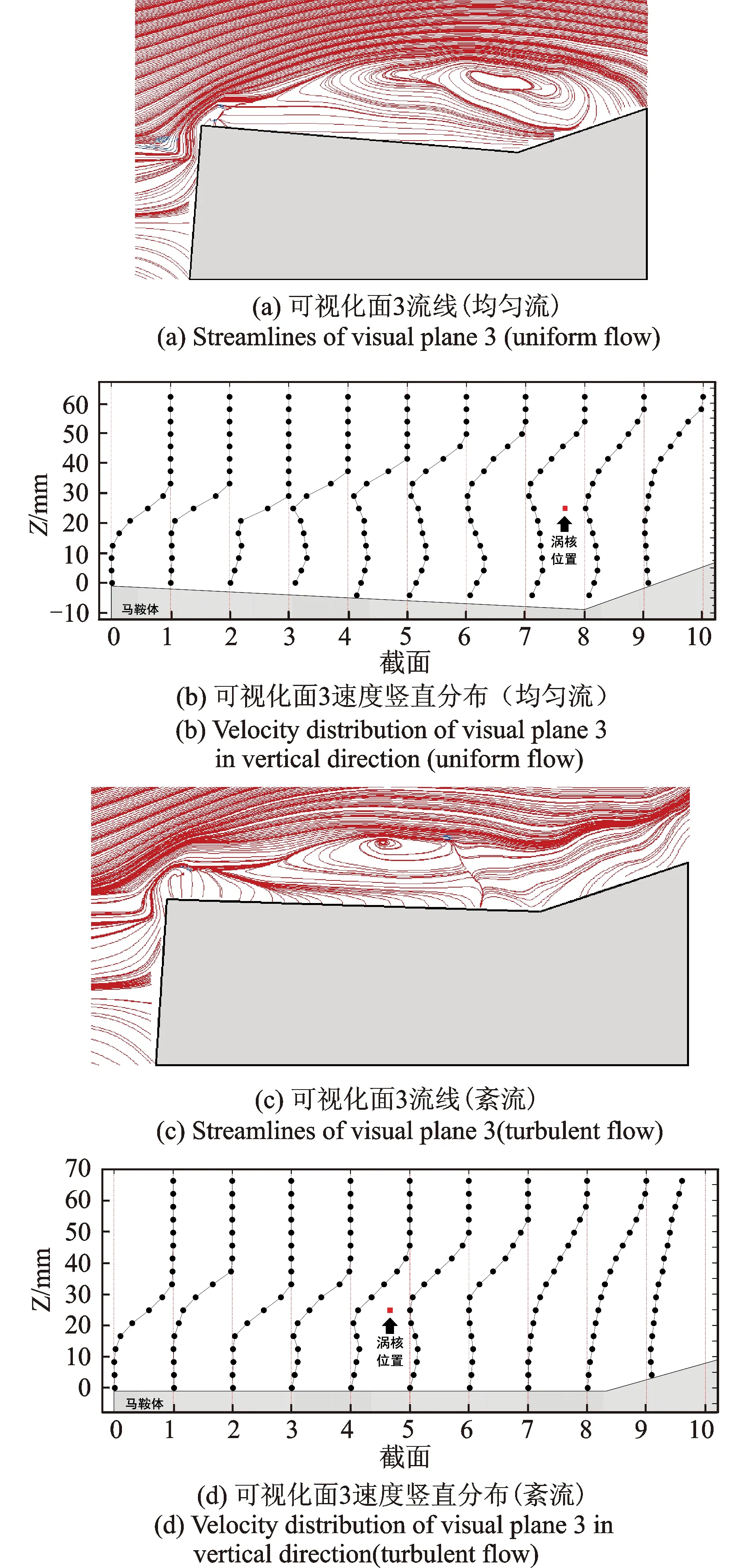
图5 可视化面3流线和速度竖直分布Fig.5 Streamlines and velocity vertical distribution of plane 3

两种来流工况下可视化面5流线如图6所示。由图6(a)可知，虽然在迎风前端出现小范围的倒流，但并未形成明显的旋涡结构，分析其原因是由于屋面存在一定的正向坡度，不利于分离剪切层的再附形成分离泡，之后气流紧贴屋面向后方发展，流线整体上表现为平直。对于格栅紊流(图6(b))，分离剪切层同样并未在屋面再附卷吸形成分离泡，但与均匀流有所不同，来流在迎风前缘顶点并未立即沿着马鞍屋盖表面进行流动分离，而是沿垂直屋盖方向继续向上运动，说明紊流下来流的分离作用更为剧烈，在风压上体现为将产生更大的抽吸力和风压脉动。

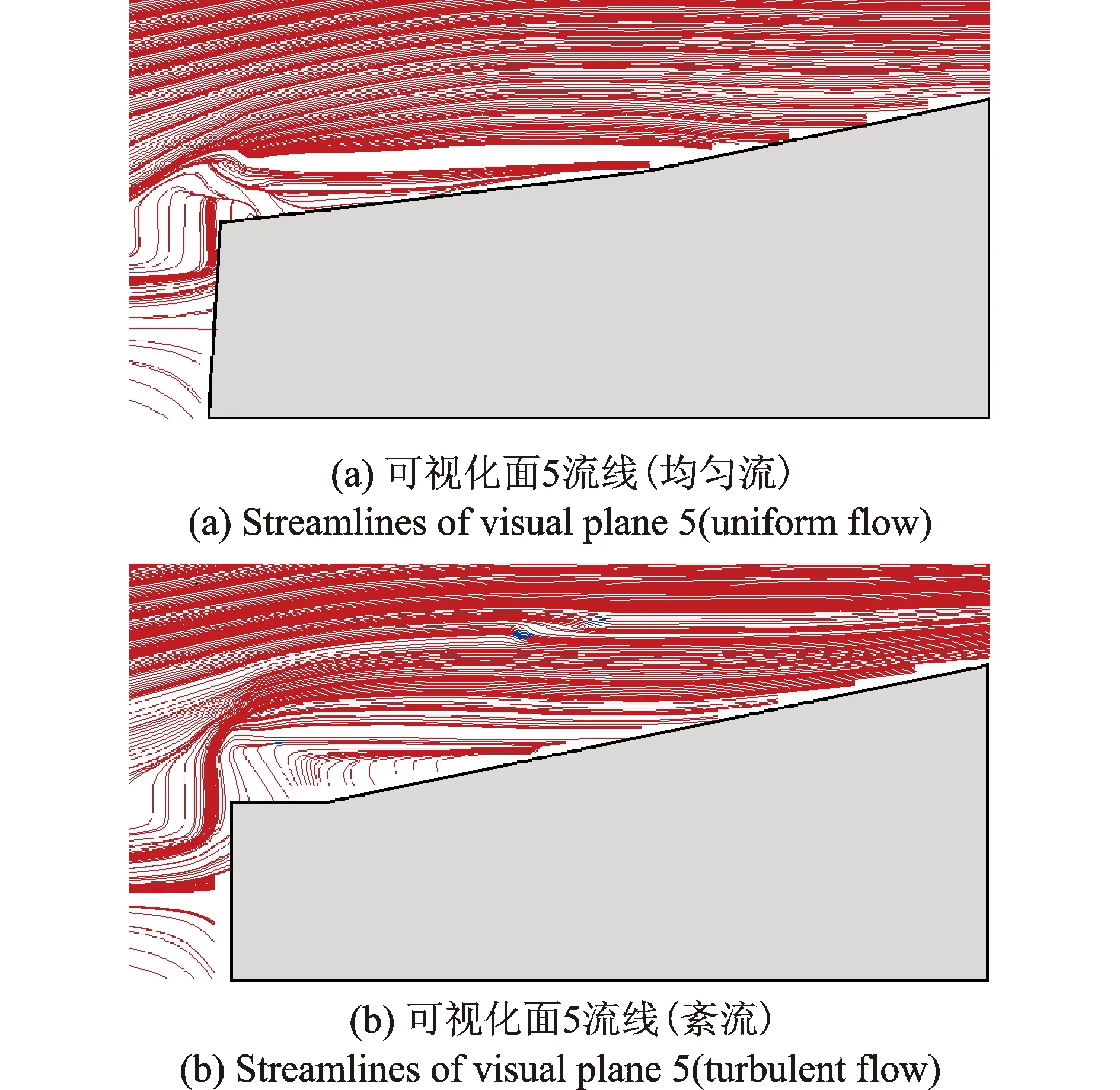
图6 可视化面5流线Fig.6 Streamlines of plane 5

2.1.2 旋涡运动瞬态特征

以可视化面1为例，图7给出了均匀流下马鞍屋盖表面旋涡的瞬时流线图。如图7(a)所示，剪切层在迎风高点处分离后卷吸成旋涡，分离泡在此刻向内卷吸为涡旋收缩状态。从图7(b),(c)中可以看出，此时分离泡为放大状态，旋涡向外扩散释放气体，旋涡面积增大。而在图7(d)中，稳定的旋涡在向外扩大的同时促使剪切层上升，产生一个次级旋涡且旋转方向与主涡相反，在主涡的作用下，屋面的分离区将引起稳定的强吸力。但由于次级涡的旋转方向与主涡相反，其产生的相反涡旋与主涡相互作用会导致屋面脉动较大。如图7(e),(f)所示，主涡和次级涡合二为一，再次转变为收缩状态，之后逐渐破裂耗散。由以上分析可以得出，分离泡内部存在一种大尺度的低频不稳定性，在此作用下分离泡不断收缩和放大，稳定发展的分离泡在其涡核正下方形成巨大的抽吸作用，在向外扩散的同时会二次卷吸形成次级涡，造成屋盖较大的风压脉动。

图7 分离泡瞬时形态特征(均匀流，可视化面1)Fig.7 Instantaneous characteristics of separation bubble (uniform flow，plane 1)

对PIV试验中得到的50张图片进行数据统计，每幅图片中首个旋涡的涡核离迎风前缘的距离如图8所示。对比两种来流工况下涡核离迎风前缘距离可以得到：来流为均匀流时，剪切层卷吸形成稳定旋涡的位置集中在0.3L～0.4L(L见图2)，即离距离迎风前缘为60～80 mm。而格栅紊流造成的动荡促使分离剪切层向屋面靠近，气流更加接近于迎风前缘；增大湍流能量能增强剪切层的卷吸作用，其首个涡核平均位置主要分布于0.2L～0.3L，即离迎风前缘距离为50～60 mm，在此区域范围风吸力将达到极大值。由此可见，湍流度是决定分离泡结构形态的主要前提，湍流中的小尺度湍流成分促使分离剪切层流线曲率减小，使其较早再附形成分离泡；而大尺度湍流成分则可以加快旋涡的旋转[8-10]。

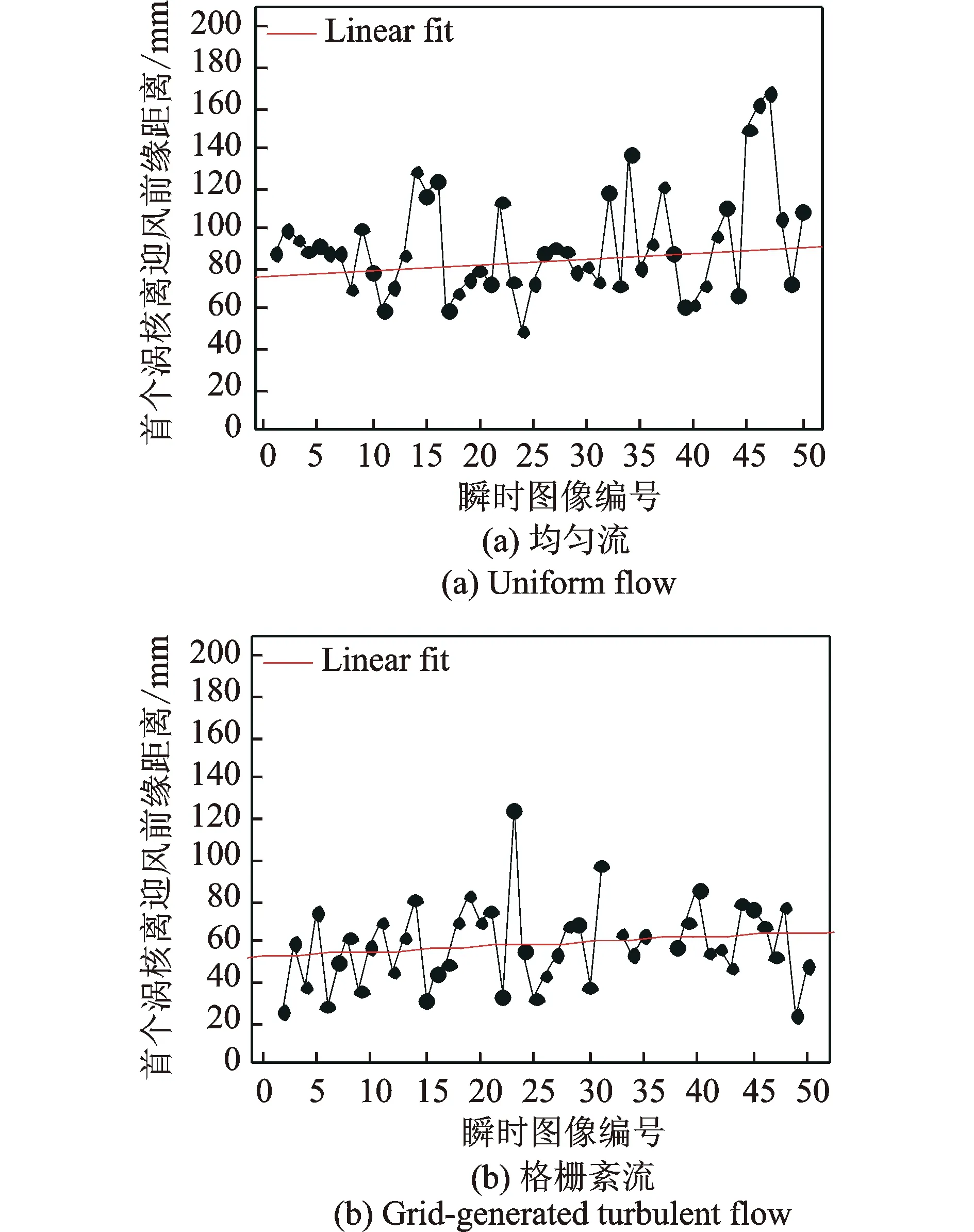
图8 涡核离迎风前缘距离Fig.8 Distance between vortex core and the leading edge

2.2 不同来流工况、不同矢跨比和不同低点高度的马鞍屋盖PIV试验结果对比分析

图9给出了矢跨比为1/12和1/6、低点高度分别为56和28mm的马鞍屋盖表面旋涡特征参数的比较，图中的虚线范围表示旋涡横截面积S。由图对比分析可知：①不同来流工况下(均匀流和格栅紊流)：来流为均匀流时，分离泡的平均再附长度较长，涡核位置高度较高，直接导致旋涡的影响区域增大。湍流度的增大旋涡再附长度变短。②不同矢跨比(1/6和1/12)：涡核离迎风前缘距离和旋涡截面积受马鞍曲面矢跨比影响较大。矢跨比越大，X和S均在增大，而Z受矢跨比影响较小。③不同低点高度(28和56 mm)：相对于矢跨比而言，低点高度的不同对X，Z和S影响均较小，进一步说明不同低点高度下马鞍屋面旋涡形态特征较为相似。

图9 涡核位置及旋涡面积对比(可视化面1)Fig.9 Comparative map of vortex core position and vortex area (visual plane 1)

3 刚性模型测压试验

3.1 试验概况

本文的风洞试验是在湖南大学风工程试验研究中心大气边界层风洞HD-2的高速试验段完成的，试验段尺寸为长17 m、宽3 m、高2.5 m。为了更好地与PIV模型相对应，测压模型是按照PIV试验模型等比例放大。4个马鞍屋盖的底面投影均为正方形，尺寸为780 mm×780 mm(图10(a))，矢跨比分别为1/6和1/12。两种矢跨比的马鞍模型分别有低点高度为104 mm和208 mm。试验模型均为刚性模型，四周封闭，采用有机玻璃制成。如图10(b)所示，屋面共布置336个测点，每个可视化面内均匀布置测点，以压力向下为正，向上吸力为负。试验来流风速控制在10 m/s，模拟的风场有均匀流场和格栅紊流场，马鞍屋盖平均高度处的湍流度维持在10%。试验中每个测点采集6600个数据，采样时长为19.934 s。

各测点的风压值采用无量纲压力系数表示

(1)

式中Pi为模型第i个测孔测得系统修正后的表面风压值；P0和P∞分别为参考点处的平均总压和平均静压。对数据进行处理得到平均风压系数Cpmean和脉动风压系数Cprms。

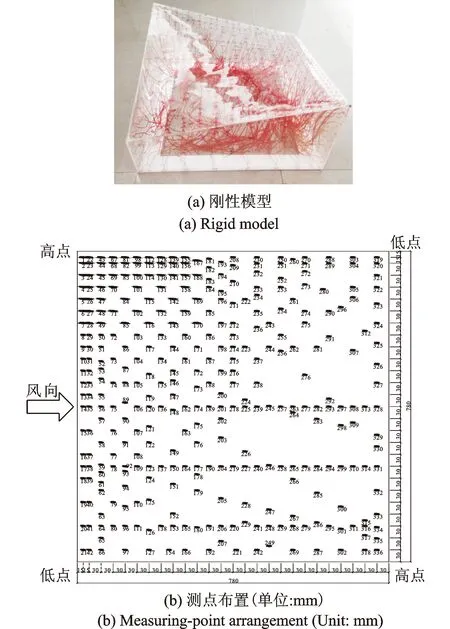
图10 马鞍屋盖模型和测点分布Fig.10 Model of the saddle roof and its tap locations

3.2 试验结果

3.2.1 分离泡作用下马鞍屋盖表面风压分布

由于不同矢跨比的马鞍屋盖表面风压分布特征相似，本次的研究对象设定为矢跨比1/12低点高度208 mm的马鞍模型。图11为马鞍屋盖表面的平均、脉动和最大值风压系数等值线图，图11(a)和(d)的阴影部分为Cpmean小于-0.8的区域；图11(b)和(e)的阴影部分为Cprms大于0.2的区域；图11(c)的(f)的阴影部分为Cpmax小于-1.5的区域。对比分析可见，均匀流场下屋面平均和最大风吸力较大，但脉动风压较小；格栅紊流下平均和最大风吸力较小，但屋盖表面的脉动风压较大且极大值区域沿低点对角线分布较广。这是因为在均匀流场中，来流未经任何阻碍而直接作用于屋面，风吸力的平均效应明显，但由于来流中的湍流成分较少，风压脉动也较小；在湍流场中，来流经过格栅使得湍流成分增加，屋面风压脉动也随之增大，然而来流动能损耗使得屋面平均吸力减小。因此，均匀流场下屋面能引起较大的平均风吸力，而湍流场中脉动风吸力则显著增强。两种来流下迎风低点附近区域的平均、脉动和最大值风压均达到最强。

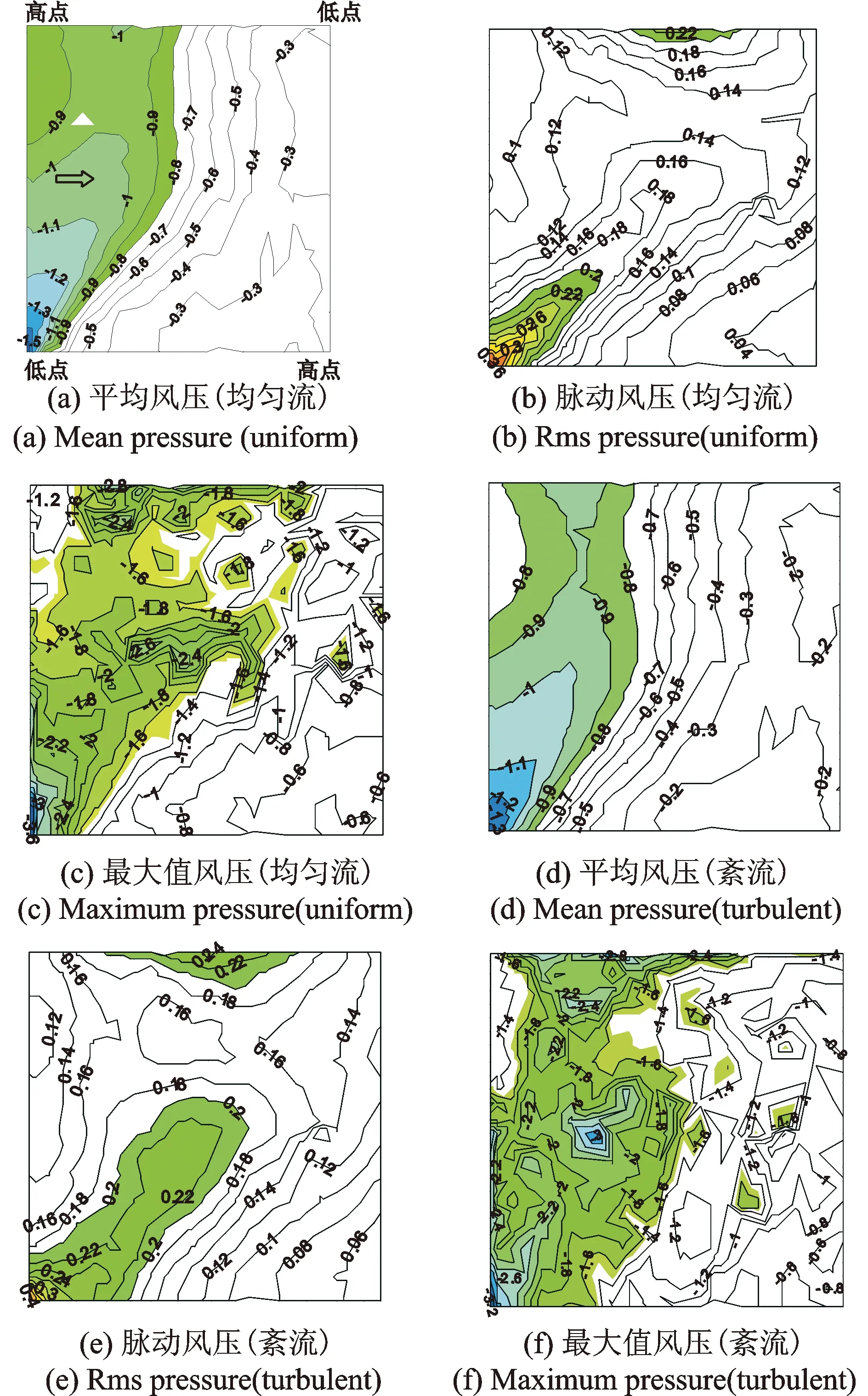
图11 马鞍屋盖表面风压分布等值线图Fig.11 Contour maps of pressure distribution on saddle roof

3.2.2 顺风向测点平均、脉动风压变化曲线

为了得到PIV试验中可视化面内的风压分布规律，以迎风高点和迎风低点测点列为例进行讨论。各测点的平均、脉动风压如图12所示。图中的横坐标为无量纲坐标X/L，其中X表示各测点与迎风边的距离，L为模型的底面边长。由图12(a)和(c)可知，对于面1而言，在X/L=0～0.5之间，平均吸力强劲，旋涡作用突出，处在分离泡的影响范围之内，均匀流工况平均吸力最大值高于格栅紊流场；在X/L=0.5～0.75之间，平均吸力迅速衰减，此时旋涡作用有所减弱，但由于再附作用脉动吸力在此区域达到最大值；从X/L=0.75开始，旋涡逐渐脱落，平均吸力趋于平稳而脉动压力快速下降。由图12(b)和(d)可知，从低点到高点存在的正向坡度引导气流向上运动，导致屋盖迎风顶点附近平均、脉动吸力都达到屋盖的最大值，随着来流往下游发展，平均、脉动风压快速下降而后趋于平稳。

3.2.3 顺风向脉动风压谱

以顺风向测点列为研究对象，分为迎风高点Rank1和迎风低点Rank2测点列,如图13所示。图14给出了均匀流下Rank1的脉动风压谱，并进行了无量纲化处理[11-12]。将马鞍屋面分为4个区域：①前缘迎风区(测点1～81)。来流在迎风前缘分离阶段，低频脉动为主控，屋面风压主要受到来流远场脉动的直接作用，在风压数值上体现为测点1,43,81的平均和脉动风压系数均在不断增大(见表1)。②主涡作用区(测点98～181)。随着剪切层再附形成分离泡，风压脉动中的中频成分增加，旋涡的近场脉动成为关键因素。从谱值上可以看出，从测点112至测点139，中频段的谱峰值逐渐增加，测点的平均和脉动风压系数也相应增大，测点139处附近达到最大值(表1)。③再附区(测点208～270)，此区域中频依然为主导，但峰值有所下降。由于气流垂直于屋面方向向下运动形成再附，导致脉动吸力达到最大值(表1，测点208)。④旋涡脱落区(测点288～319)。当来流到达背风面边缘时，由中频转向高频成分，这是由于旋涡脱落分解成大量的微尺度涡，由于其具有较大的黏性应力和剪切变形，使湍流能量快速耗散，直接导致风压脉动系数减小。

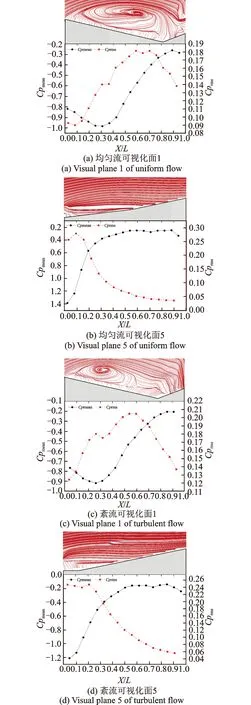
图12 顺风向测点平均、脉动风压分布Fig.12 Variation of longitudinal mean and fluctuating pressures

均匀流下Rank2的脉动风压谱如图15所示，可以得出，从测点21开始，风压谱从低频到高频为不断上升趋势，谱峰值在高频段达到最大值(表2，21点)，该区域受到特征湍流影响显著。随着来流往下游发展，中频能量开始减少。图15(b)中的高频成分说明存在小尺度湍流促使旋涡形成，但由于迎风低点至背风面为正向坡度，屋面上并未形成旋涡，风压系数从迎风低点处开始呈一直下降趋势。当来流到达边缘测点336时，受到马鞍高点的干扰作用，低频有所增加，平均风压也随之增大(表2，336点)。

图13 分离泡作用下马鞍屋面分区示意Fig.13 Sub regions of saddle roof under separation bubble

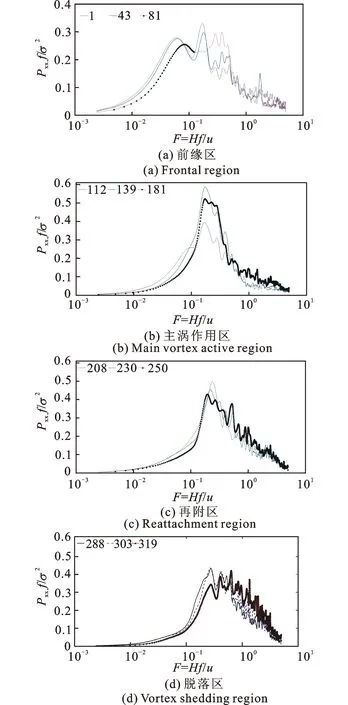
图14 马鞍迎风高点处测点脉动风压谱(均匀流)Fig.14 Fluctuating wind pressure spectrum of middle high rank on saddle roof (uniform flow)

表1 马鞍迎风前缘高点处测点风压时程统计值(均匀流)

Tab.1 Time series statistics of high point rank on saddle roof (uniform flow)

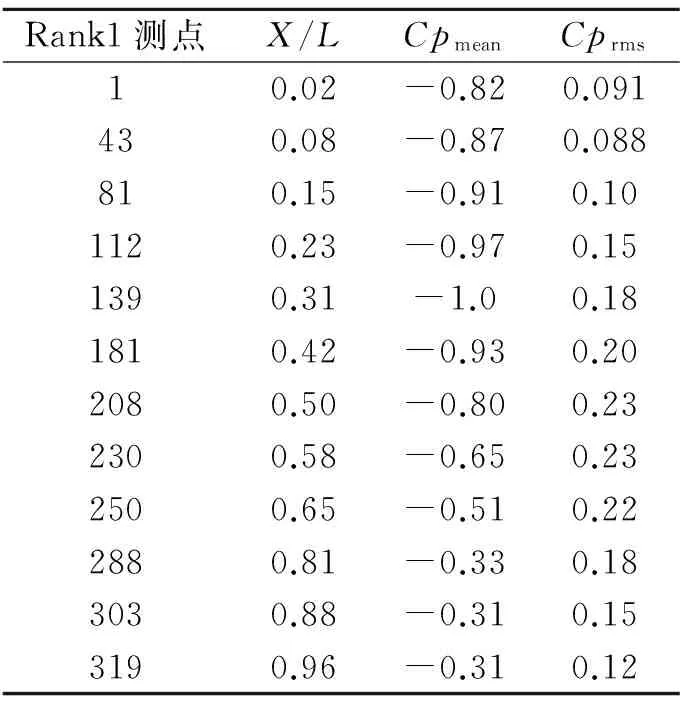
Rank1测点X/LCpmeanCprms10.02-0.820.091430.08-0.870.088810.15-0.910.101120.23-0.970.151390.31-1.00.181810.42-0.930.202080.50-0.800.232300.58-0.650.232500.65-0.510.222880.81-0.330.183030.88-0.310.153190.96-0.310.12

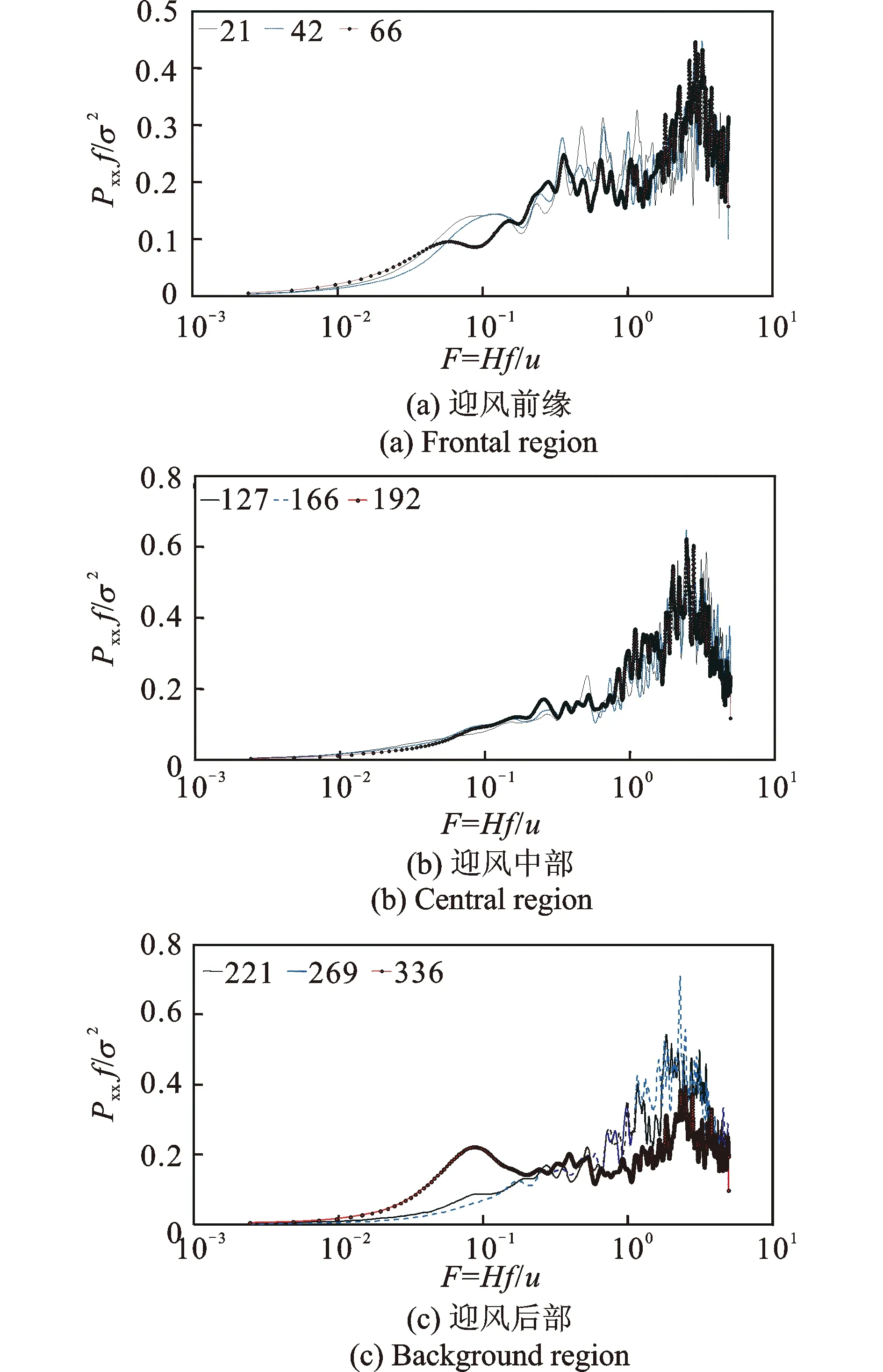
图15 马鞍迎风低点处测点脉动风压谱(均匀流)Fig.15 Fluctuating wind pressure spectrum of low rank on saddle roof (uniform flow)

表2 马鞍迎风前缘低点处测点风压时程统计值(均匀流)

Tab.2 Time series statistics of low point rank on saddle roof (uniform flow)

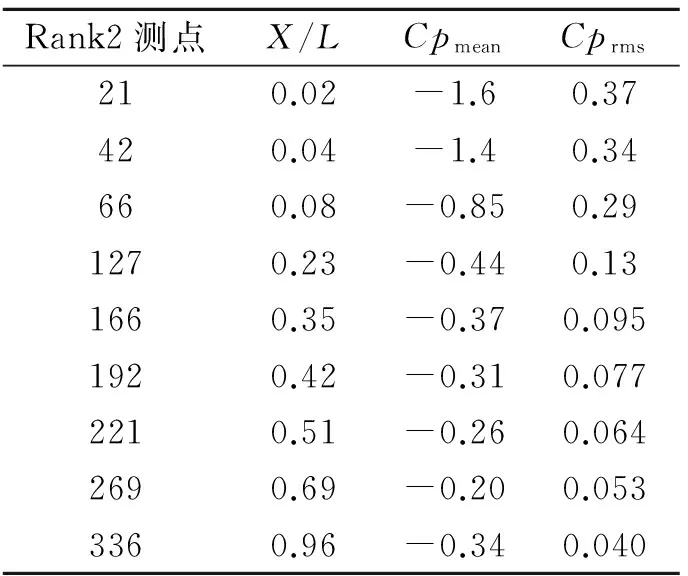
Rank2测点X/LCpmeanCprms210.02-1.60.37420.04-1.40.34660.08-0.850.291270.23-0.440.131660.35-0.370.0951920.42-0.310.0772210.51-0.260.0642690.69-0.200.0533360.96-0.340.040

格栅紊流下测点风压谱分布与均匀流工况较为类似，但紊流下迎风高点前缘处的谱峰值显著增大，分析其原因是由于来流受到格栅装置的阻碍，导致来流中的大尺度湍流成分增加。而在迎风低点前缘处，紊流下迎风前缘受来流中的湍流成分影响显著，风压谱的低频段和中频段均有谱峰值，低频段能量明显强于均匀流，以致脉动风压有所增大。当来流到达屋盖后部区域高点时，低频脉动增加，此情况与均匀流相同。

4 马鞍屋面旋涡三维形态及分区体型系数

根据PIV流动显示试验5个可视化面的试验结果综合分析，得到马鞍屋盖表面旋涡结构的时均三维形态及屋盖各区域最大风压系数的分布，如图16所示，具有以下几点特征：

(1)来流为均匀流时，迎风高点至迎风中点半个马鞍区域出现典型的分离泡现象，总体在顺风向为扁的椭圆形，旋涡几乎横跨整个屋面，涡核位置处于马鞍屋面偏后位置，3个截面的涡核高度基本一致。迎风高点和迎风中点处截面的风吸力最大值点离迎风前缘距离一致，说明了从迎风高点到中点位置分离泡的流动是二维的，风压在横风向表现出强烈且均一的相关特征。在迎风中点与迎风低点区域，由于马鞍屋盖自身的曲面特性，旋涡结构迅速衰减，在靠近低点的横风向边缘，流线平直没有明显的旋涡形成。迎风墙面的上半部分荷载主要表现为压力作用，在墙面的中部达到最大值0.8，而在迎风低点处墙面底部出现了较大的风吸力，此处为来流直接碰撞墙面后向下卷吸成马蹄涡造成的。屋盖表面的风荷载以吸力为主，在模型的迎风低点附近吸力达到最大值-1.6且变化梯度大，脉动风压最大值也出现在迎风低点处，极大值影响范围小。随着来流向后方发展，风吸力区域稳定。

(2)来流为格栅紊流时，分离泡三维结构与均匀流工况较为类似，但有两点不同：迎风高点至中点区域的分离泡体积明显小于均匀流工况，涡核位置离迎风前缘距离较近。这是由于紊流中的小尺度湍流促使剪切层卷吸旋涡，而中尺度湍流加快了旋涡的旋转，导致后来的流体提前再附于屋盖表面；通过屋面风压系数比较可以看出，格栅紊流工况下分离泡涡核正下方风吸力达到最大值-0.9，湍流度的增大对平均风荷载影响较小，均匀流场下风压系数均大于格栅紊流场。主要原因是均匀流下的分离作用强度更为集中，同时来流湍流度对风压分布影响主要集中于屋盖迎风前缘区域，对其他区域风压系数影响较小。因此，在进行大跨度马鞍屋盖工程设计时，应特别注意迎风低点处附近区域及拐角区。

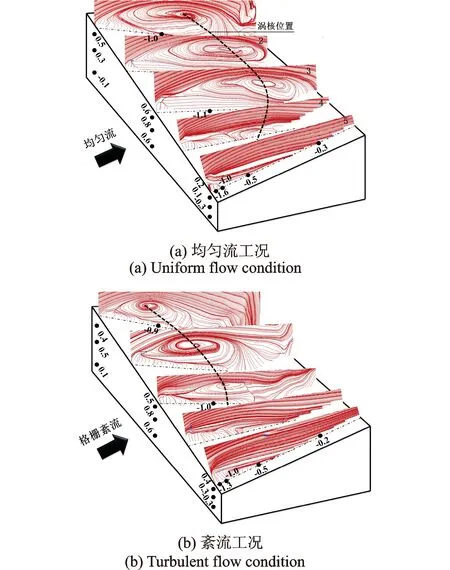
图16 分离泡三维时均形态Fig.16 3D time-average shape of separation bubble

对于马鞍屋盖结构，中国现行的《建筑结构荷载规范》(GB 50009-2012)中并没有明文规定。如前文所述，分离泡作用下的马鞍屋盖迎风高点至迎风中点区域可以分为：主涡作用区、旋涡再附区和旋涡脱落区。在此基础上考虑到迎风低点处风吸力最强，因此最终将马鞍屋盖表面划分为4个区域，此时各区域体型系数μs按下式确定

(2)

式中Cpmean,i和Si分别对应第i测点的平均风压系数和其所属的平均面积；S为计算区域的总面积。利用式(2)得到的马鞍屋盖表面分区体型系数如图17所示。

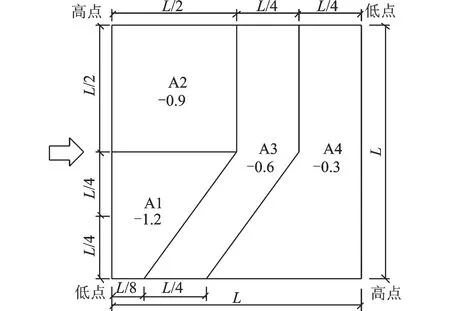
图17 分离泡作用下马鞍屋盖分区体型系数Fig.17 Shape factors for sub regions of saddle roof

5 结 论

本文通过大跨马鞍屋盖表面旋涡的流动显示试验，观察了不同来流工况下马鞍屋盖表面的旋涡现象，基于旋涡作用机理，对屋面顺风向风压数值变化和脉动风压谱进行研究，推断出马鞍屋盖分离泡的三维形态特征及分区体型系数，所得主要结论如下：

(1)来流为均匀流时，马鞍屋盖仅在迎风高点至迎风中点区段形成分离泡，其形态为扁的椭圆形，旋涡横跨整个屋面。在迎风中点至低点区域则无法形成旋涡。屋盖迎风高点处前缘测点风压谱以低频为主导，随着测点后移逐渐向中高频过渡，谱带变窄且峰值增大。而在迎风低点处，风压谱从低频到高频为不断上升趋势，谱峰值在高频段达到最大值。

(2)格栅紊流下的分离泡同样只出现在迎风高点至中点区域，旋涡横截面积明显小于均匀流，且涡核位置离迎风前缘更近。紊流下迎风前缘处测点的低频段能量要显著高于均匀流。两种来流工况下，屋盖表面的风荷载都以吸力为主，最大平均风压和脉动风压都位于迎风低点附近且变化梯度较大，其他区域变化相对平缓。随着来流向下游发展，涡量将逐渐耗散，风吸力逐渐减弱。

(3)不同矢跨比下马鞍屋盖表面分离泡的三维形态较为类似，但随着矢跨比的增大，涡核离迎风前缘的距离及旋涡的横截面积均在增大，而矢跨比对分离泡涡核高度影响较小。

(4)考虑到分离泡的作用，中国建筑荷载规范中关于马鞍屋盖结构体型系数没有明文规定，本文根据马鞍屋盖表面旋涡的三维形态特征给出了来流垂直于迎风墙面时屋面的4个分区及相应的体型系数，分别为马鞍迎风低点区(-1.2)、分离泡主涡作用区(-0.9)、旋涡再附区(-0.6)和旋涡脱落区(-0.3)。

[1] Saathoff P J, Melbourne W H. Effects of free-stream turbulence on surface pressure fluctuations in a separation bubble [J]. J. Fluid Mech., 1997, 337(04): 1—24.

[2] Kyung Chun Kim, Ho Seong Ji, Seung Hak Seong. Flow around a 3-D rectangular prism in a turbulent boundary layer [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91: 653—669.

[3] Partha P Sarkar, Zhongshan Zhao, Kishor C Mehta. Flow visualization and measurement on the roof of the Texas Tech building [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 69-71:597—606.

[4] Lauent Brizzi, Gerard J Poitras, Yves Gagnon. PIV measurements around 2D and 3D building models [J]. Int.J. Engineering Systems Modelling and Simulation, 2008, 1(1): 48—62.

[5] Shinji Ito, Yasuo Okuda, Hitomistu Kikitsu, et al. Experimental study on flow and pressure fields over the roof of a cube by PIV measurements [J]. Journal of Wind Engineering, 2006, 108: 435—438.

[6] 李金国. 边界层风洞和建筑物标模的流迹与测压试验研究[D]. 上海: 同济大学, 2007.

Li Jinguo. The research on boundary layer wind tunnel，the trail of the standard building model and pressure experiment[D]. Shanghai: Tongji University, 2007

[7] Ye Jihong, Dong Xin. Improvement and validation of a flow model for conical vortices [J]. Wind and Structures, 2014, 19(2): 113—144.

[8] Banks D, Meroney R N, Sarkar P P, et al. Flow visualization of conical vortices on flat roofs with simultaneous surface pressure measurement [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000, 84: 65—85.

[9] Kawai H. Structure of conical vortices related with suction fluctuation on a flat roof in oblique smooth and turbulent flow[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 69-71:579—588.

[10]Masaru Kiya, Kyuro Sasaki. Structure of large-scale vortices and unsteady reverse flow in the reattaching zone of a turbulent separation bubble[J]. Journal of Fluid Mechanics, 1985, 154: 463—491.

[11]Mostafa N H,Hajj M R, Zeiger M D, et al. Space/time characteristics of pressure fluctuations in separation regions [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90: 415—426.

[12]Suresh Kumar K, Sathopoulos T. Power spectra of wind pressure on low building roofs [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 74-76: 665—674.

3-D flow characteristics of separation bubble around the saddle roof

YEJi-hong，SUNHu-yue

(Key Laboratory of Concrete and Pre-stressed Concrete Structure of Ministry of Education, Southeast University,
Nanjing 210018, China)

Through Particle Image Velocimetry (abbr.PIV), flow visualization of separation bubble around saddle roofs was conducted in a wind tunnel. The vortex section morphology and time-average, instantaneous streamlines and vorticity field distribution were obtained under high and low windward point in uniform and grid-generated flow field. The characteristics of vortices were compared in different flow conditions. Velocity distribution rule of the visual plane on the roof surface was summarized. Results indicated that when the wind direction perpendicular to windward on the leading edge of the roof, the area between the high point windward and middle point windward will appear typical separation bubble phenomenon. Due to the positive slope of the saddle roof, there was no separation bubble at the low windward point. The reattached length is almost across the whole roof in uniform flow, while the vortex core was closer to the windward edge in turbulent flow and the vortex cross-sectional area significantly less than in uniform flow condition. With the result of the wind tunnel pressure measurement, the fluctuating wind pressure spectrum at different height of the windward were analyzed and established the spectrum evolution relationship between energy and vortex movement or turbulence scale. Three-dimensional morphological characteristics were obtained by analysis of the multiple visual planes comprehensive arrangement. The saddle roof was divided into four regions accordingly and put forward reasonable partition shape coefficient, providing reference to the large-span saddle roof wind resistance design.

wind load； saddle roof; separation bubble; PIV; wind pressure spectrum

2015-07-08；

2016-03-24

国家杰出青年科学基金资助项目(51125031); 江苏省普通高校研究生科研创新计划资助项目(KYLX_0157); 中央高校基本业务费专项资金资助项目(3205005718)

TU312+.1

：A

1004-4523(2016)06-1097-11

10.16385/j.cnki.issn.1004-4523.2016.06.020

叶继红(1967—)，女，教授。电话：(025)83795023；E-mail:yejihong@seu.edu.cn