轨道型非线性能量阱对高层结构脉动风振的控制仿真①

刘中坡，乌建中，王菁菁，吕西林

(1.同济大学机械与能源工程学院，上海 201804；2.同济大学土木工程防灾国家重点实验室, 上海 200092)

轨道型非线性能量阱对高层结构脉动风振的控制仿真①

刘中坡1，乌建中1，王菁菁2，吕西林2

(1.同济大学机械与能源工程学院，上海 201804；2.同济大学土木工程防灾国家重点实验室, 上海 200092)

介绍了轨道型被动NES(Nonlinear Energy Sink)，并对附加NES装置的5层钢框架进行了白噪声激励下的振动台实验，结果表明了NES能在多个频率范围内抑制结构振动。基于NES的这种优点，将其应用到高层结构的风振控制上。采用线性回归方法的AR模型，模拟了不同高度处的脉动风速时程作为建筑结构的外部激励。以脉动风激励下高层建筑顶层的加速度为控制目标，对NES的质量、轨道表达式和黏滞阻尼参数进行了一系列优化，选择较优的参数对NES控制下某结构的脉动风致振动进行了仿真计算。计算结果表明:NES可以有效减小脉动风作用下建筑结构的最大加速度与加速度均方根，并且其可以同时减小结构多个模态的振动，从而提高风载荷下高层建筑的舒适度。

风振控制; 高层建筑； 脉动风； NES； AR模型

引 言

对于高层建筑，地震和强风作用下引起的结构动力反应，会影响结构的安全和使用的舒适度。传统的结构设计通过加强结构强度来满足结构的安全和使用要求，在实际工程上经济性较差。为了减小结构反应，常见的是通过在建筑结构物的某些部位设置调谐质量阻尼器(Tuned Mass Damper, TMD) 以减小地震和风振反应。然而传统线性TMD的适用频带较窄,只有多个吸振器联合作用才能实现多模态控制。另外一种方法是利用非线振子的宽频吸振特性进行减振, 很多学者持续对其进行了大量的研究。国外学者Roberson最早对应用非线性吸振器进行振动控制做了研究[1]，提出用非线性刚度吸振器可以使得吸振带宽有所增加。Vakakis等把一个非线性振子与一个线性振子连接到一起,并对整个系统在冲击载荷下的共振现象进行了研究[2]，Gourdon通过数值计算的方法验证了该系统并指出非线性振子优于传统的线性吸振装置[3]。Vakakis把该类刚度为立方非线性刚度的振动控制振子命名为非线性能量阱(Nonlinear Energy Sink,简称NES)[4]。Jiang研究了NES与单自由度振子在外界正弦激励的响应[5]。Starosvetsky等开展了NES参数优化的研究工作，并在试验中证实了其振动控制效果优于TMD[6]。国内学者也对NES开展了若干研究;张也弛、孔宪仁等对两自由度NES在简谐荷载下的力学特性与振动控制效果使用数值方法进行了研究[7];王菁菁采用数值仿真的方法对轨道型NES的轨道参数进行了优化计算[8]，并使用数值方法验证了这种类型NES在冲击载荷与地震波激励下的宽频控制特性。目前NES的应用研究主要集中在航天、机械与汽车领域，在建筑结构领域的应用研究较少，本文在文献[8]的研究基础之上对轨道型NES应用到建筑结构风致振动的控制进行探讨。

1 轨道型NES及其振动控制特性

1.1 安装NES的结构运动方程

轨道型NES由轨道、质量块和阻尼器构成，轨道在竖直平面内弯曲，其形状函数一般为高阶多项式用于给在其之上滑动的质量块提供非线性的回复力。质量块沿轨道运动，其运动方向与结构需要控制的方向平行，如图1(a)所示。当被控结构振动的时候，结构与NES之间产生相对运动，被控结构振动的部分能量被传递到NES并通过NES的阻尼耗散，同时利用NES沿轨道运动时与被控结构之间相互作用，从而达到结构振动控制的目的。

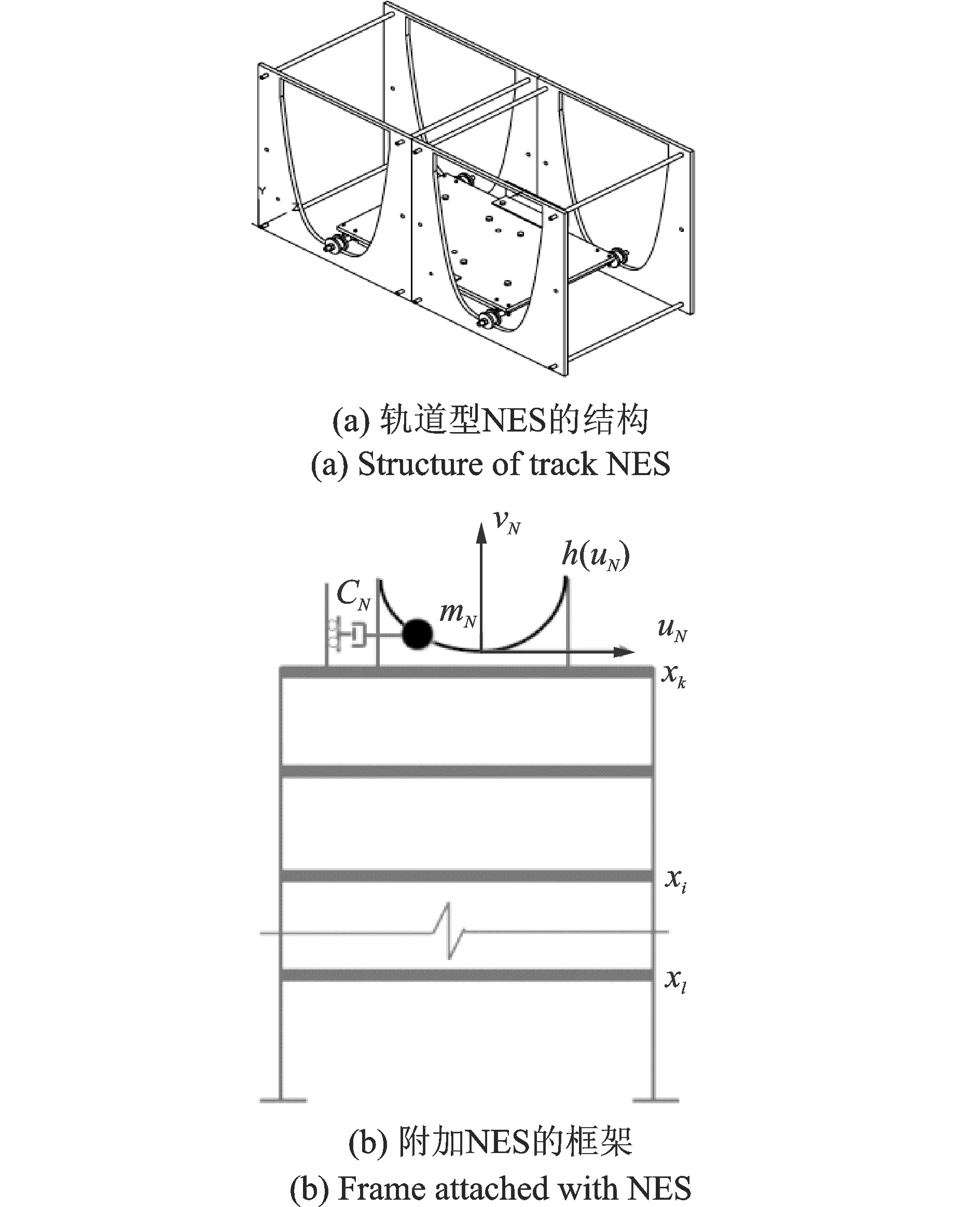
图1 NES的结构与附加NES的多层框架模型Fig.1 Multi-story frame with NES and structure of track NES

附加了NES的框架结构如图1(b)所示，使用拉格朗日方程建模得到结构与NES运动方程为:

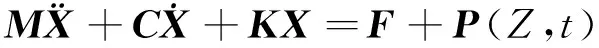
(1)

(2)

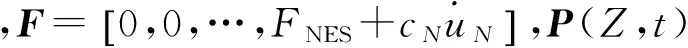
(3)

式中h(uN)为NES滑道形状函数。

从方程(2)的表达式可以得出，轨道型NES的回复力FNES与质量块的位移、速度有着强非线性的关系。使用轨道型NES实现宽频振动控制就是利用了非线性振子振动频率与其自身能量水平相关的特性。与其他类型的NES类似的是，由于非线性回复力的原因，它自身振动的频率与被控结构振动的幅值、频率和振型有关。因为这3个参数影响主体结构将振动能量传递到NES的效率，而NES能否与被控结构做反相的共振与其自身能量水平高低有关[9]。不论哪种外界激励，例如白噪声、正弦波或地震波，都会引起被控结构不同幅值、振型的动力响应，从而使NES表现出不同的振动控制效果。所以，采用数值计算方法对轨道型NES进行优化的时候，需要考察不同频谱成分与幅值的外界激励作用下主体结构在无控与NES控制下的动力响应来选择较优的NES参数。

1.2 基于白噪声的随机激励作用下NES振动台试验

为了验证NES在类似脉动风这类稳态随机激励作用下的振动控制效果，将其安装在试验框架的顶层之上，振动台把最大加速度为0.04g且带宽为0～25 Hz的有限带宽白噪声沿框架的弱轴向作用到框架上，并对比同一白噪声作用下的空框架的响应。振动台试验采用0.04g有限带宽白噪声激励，虽然不能完全模拟风洞实验中的风效应，但是可以近似地模拟脉动风对结构小幅值、频谱丰富和作用时间长的激励。

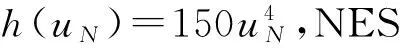
图2 框架与NES实物图Fig.2 Structure of the frame and track NES

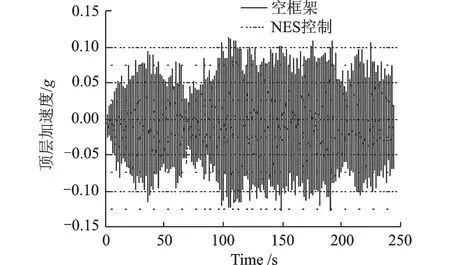
图3 框架顶层无控和有控时的加速度时程对比Fig.3 Comparison of acceleration time history at roof of the frame

在白噪声激励下，框架无控与有NES控制下的顶层加速度时程如图3所示，在时域结果中可以看到NES对框架顶层加速度控制有较好的效果。将加速度时程数据分别求绝对值的极值和均方根得到：框架无控下加速度最大值为0.128g、加速度均方根为0.043，NES控制下最大加速度为0.065g、加速度均方根为0.0171。

为了从频域中观察NES控制频率范围宽广的特性，对框架顶层加速度时程数据进行小波变换与傅里叶变换，可得到变换之后的时频能量图与加速度响应谱，分别如图4与图5(a),(b)所示。从图中可以看到相对无控状态下，框架弱轴向的前3阶模态对应频率下的振动都有不同程度上抑制，尤其以动力响应较大的1,2阶振动控制效果最为明显。将该试验工况下采集到的NES加速度值做傅里叶变换，从而得到NES的加速度响应谱如图5(c)所示。从图中可以看出，NES自身振动的频率对应框架的前3阶频率，从另外一个角度说明了NES可以作用到结构的多个模态。

振动台试验的结果说明了轨道型NES的频率范围相对传统TMD较窄作用频率范围的减震方式较优，并且对将其应用到激励类似有限带宽白噪声的脉动风载荷作用下的建筑结构振动控制提供了试验依据。

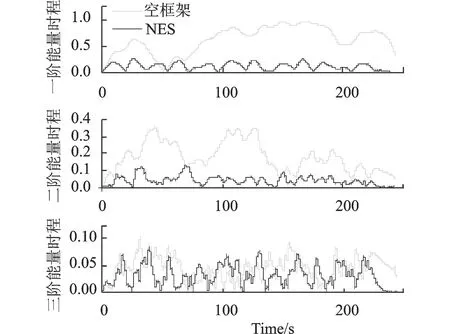
图4 框架顶层加速度无控、有控下的时频能量图对比Fig.4 Comparison of time-frequency energy diagram of top floor acceleration

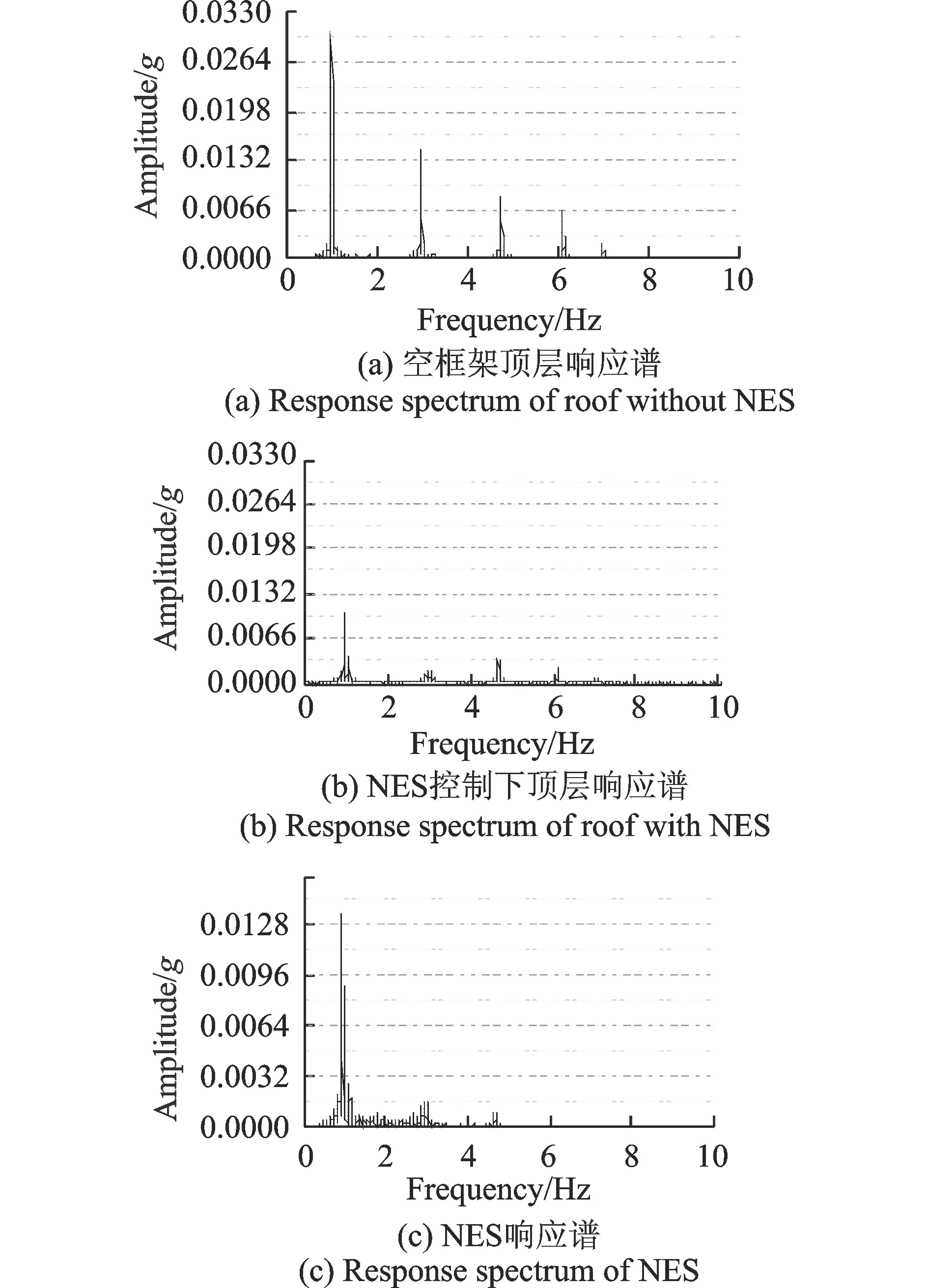
图5 顶层加速度无控、有控下的响应谱对比与NES响应谱Fig.5 Comparison of acceleration response spectrums of top floor

1.3 NES对振动控制的鲁棒性

考虑到若将NES应用到建筑结构风振控制中的话，就需要同时考虑其在地震控制下的鲁棒性。在验证了NES在较小幅值的稳态随机激励下振动控制的有效性之后，为了验证其鲁棒性又进行了不同地震波加载试验。使用抗震减震研究中经常用到的El Centro波、汶川波与日本311波作为振动台台面输入，分别在PGA为0.05g,0.1g和0.15g的条件下进行试验。由于空框架在PGA为0.15g的El Centro波作用下响应已经非常的大，再增加载荷可能会对框架有所损伤，另外为了方便与NES控制下框架的响应进行对比，所有试验工况地震波输入最大PGA设定为0.15g。在此试验过程中，试验用框架、NES与上一节中试验一致，试验结果如表1所示。

表1 框架模型顶层最大加速度和加速度响应的均方根

Tab.1 Maximum acceleration and acceleration rms values at the roof of the frame

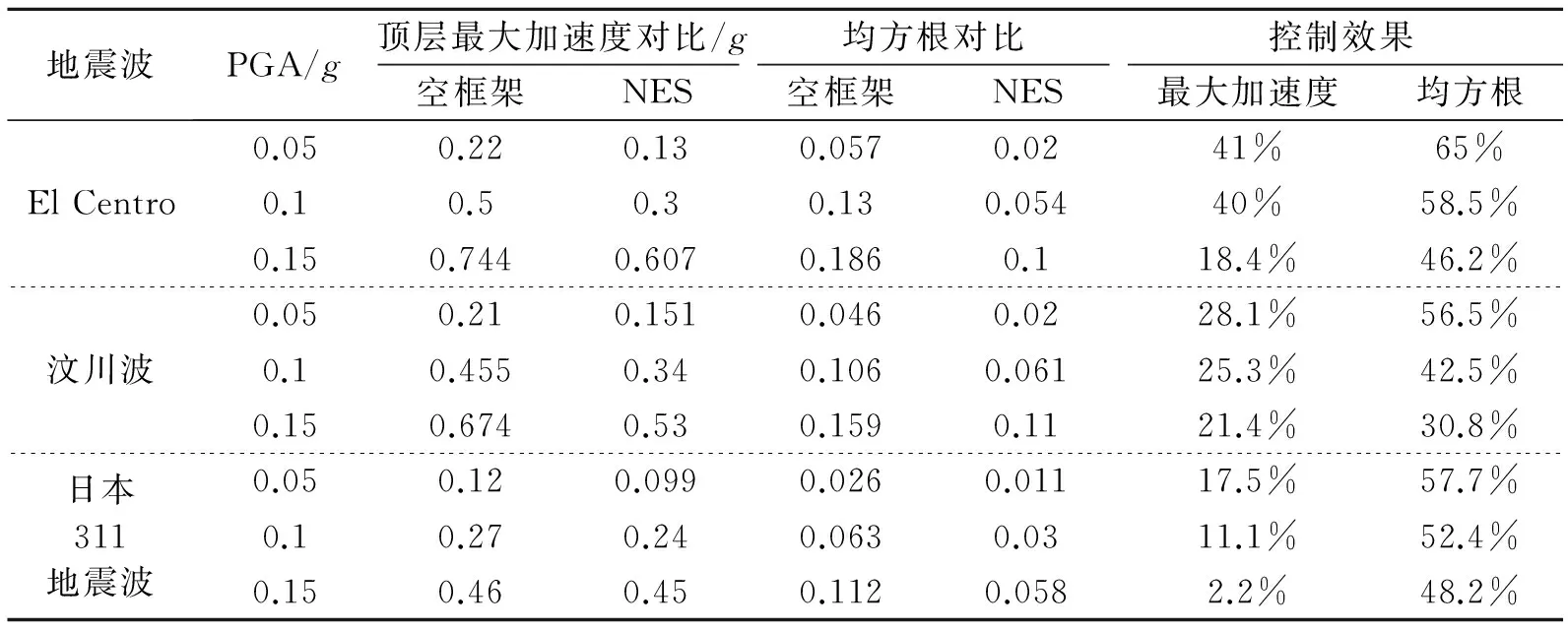
地震波PGA/g顶层最大加速度对比/g均方根对比控制效果空框架NES空框架NES最大加速度均方根ElCentro0.050.220.130.0570.0241%65%0.10.50.30.130.05440%58.5%0.150.7440.6070.1860.118.4%46.2%汶川波0.050.210.1510.0460.0228.1%56.5%0.10.4550.340.1060.06125.3%42.5%0.150.6740.530.1590.1121.4%30.8% 日本311地震波0.050.120.0990.0260.01117.5%57.7%0.10.270.240.0630.0311.1%52.4%0.150.460.450.1120.0582.2%48.2%

从试验结果可以看出，NES在本组试验中对框架顶层加速度同样起到较好的控制作用，尤其是对加速度均方根的控制效果最为明显。对绝大多数试验工况的峰值加速度都有较好的控制作用，日本311地震波激励下控制效果弱于另外两种波，是由于该地震波的频率主要集中在3.5～6 Hz范围内，而框架的一阶频率为1 Hz。在PGA为0.15g的日本311地震波激励下，空框架与NES控制下框架的顶层加速度响应谱的对比如图6(a)和(b)所示，NES加速度响应谱如图6(c)所示。相对上一节所介绍试验工况中的NES响应谱，这个试验工况下可以更为清晰地验证NES可以作用于结构的多个模态频率。本组试验验证了轨道型NES不仅仅在有限带宽白噪声激励下有效，而且对不同幅值、频谱构成的地震波作用下框架顶层的加速度与加速度方差都起到了较好的控制效果。

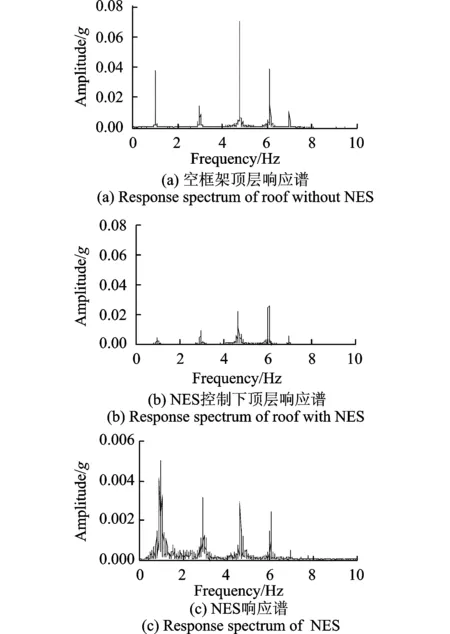
图6 311波0.15g框架顶层与NES加速度响应谱对比Fig.6 Response spectrums of the frame and the NES

2 风载荷模拟

2.1 风载荷特征

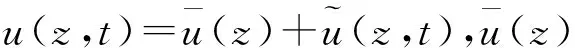
平均风速的确定：平均风速随着高度而变化的规律，也常称为平均风速剖面，常用对数律来表示

(4)

式中z,U(z)为所处高度与此高度处的平均风速,z0，U(z0)为标准参考高度与此高度处的平均风速。α为地表粗糙度系数，根据规范选择C类场地。

2.2 脉动风自功率谱与互功率谱

脉动风随时间与空间变化，一般假定为零均值的平稳高斯随机过程。根据脉动风速的这种特性，可以用脉动自功率谱、互功率谱描述脉动风速时程。对于高层建筑主要考虑水平阵风功率谱[11]，中国规范中采用的Davenport提出的脉动风速自功率谱

(5)

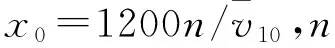
工程计算中除了考虑脉动风的自相关性描述外，还需要考虑其空间相关性。需要同时考虑结构竖向和侧向相关性时，空间任意两点的相关系数一般采用Davenport提出的表达式

(6)

式中Cx,Cz各表示为侧向与竖向的衰减系数；x1,x2,z1,z2分别为垂直于风向点的水平、垂直坐标；Vz1,Vz2为对应点的风速；n为风速谱的频率。由此可得如下的脉动风相干函数。

Svivj(x1,x2,z1,z2,n)=ρ(x1,x2,z1,z2,n)·

(7)

2.3 基于线性滤波器法的脉动风模拟

脉动风速的数值模拟方法通常使用线性滤波法与谐波叠加法, 考虑计算效率，本文采用线性滤波法中的AR模型对超高层建筑的脉动风速时程进行数值模拟。空间中M个点相关的脉动风速时程V(x,y,z,t)列向量的AR模型可以表示为

N(t)

(8)

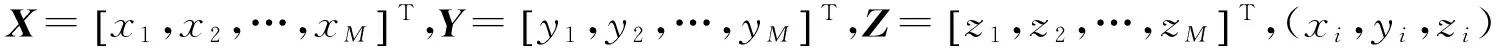
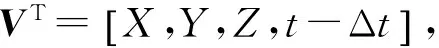
(9)

对RN做Cholesky分解得：RN=LLT。由此求得N(t)=Ln(t)。式中n(t)=[n1(t),…,nM(t)]T，其中的ni(t),i=1,…,M，为均值是0、方差是1并且彼此相互独立的正态随机过程。

表2 脉动风速模拟参数

Tab.2 Parameters of fluctuating wind speed simulation

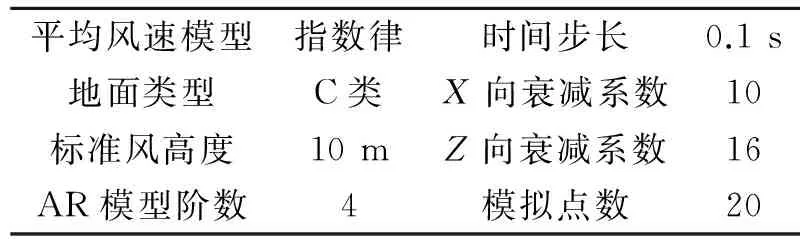
平均风速模型指数律时间步长0.1s地面类型C类X向衰减系数10标准风高度10mZ向衰减系数16AR模型阶数4模拟点数20

基于以上的推导过程，使用表2中的脉动风模拟参数在MATLAB中编写计算程序，得到的10 m高度处的脉动风速时程如图7(a)所示。为了验证模拟得到的脉动风速的准确性，将其时程变换到频域中，在双对数坐标中与Davenport目标谱进行比较，如图7(b)所示，可以看出使用AR方法模拟得到的风速时程是可靠的。

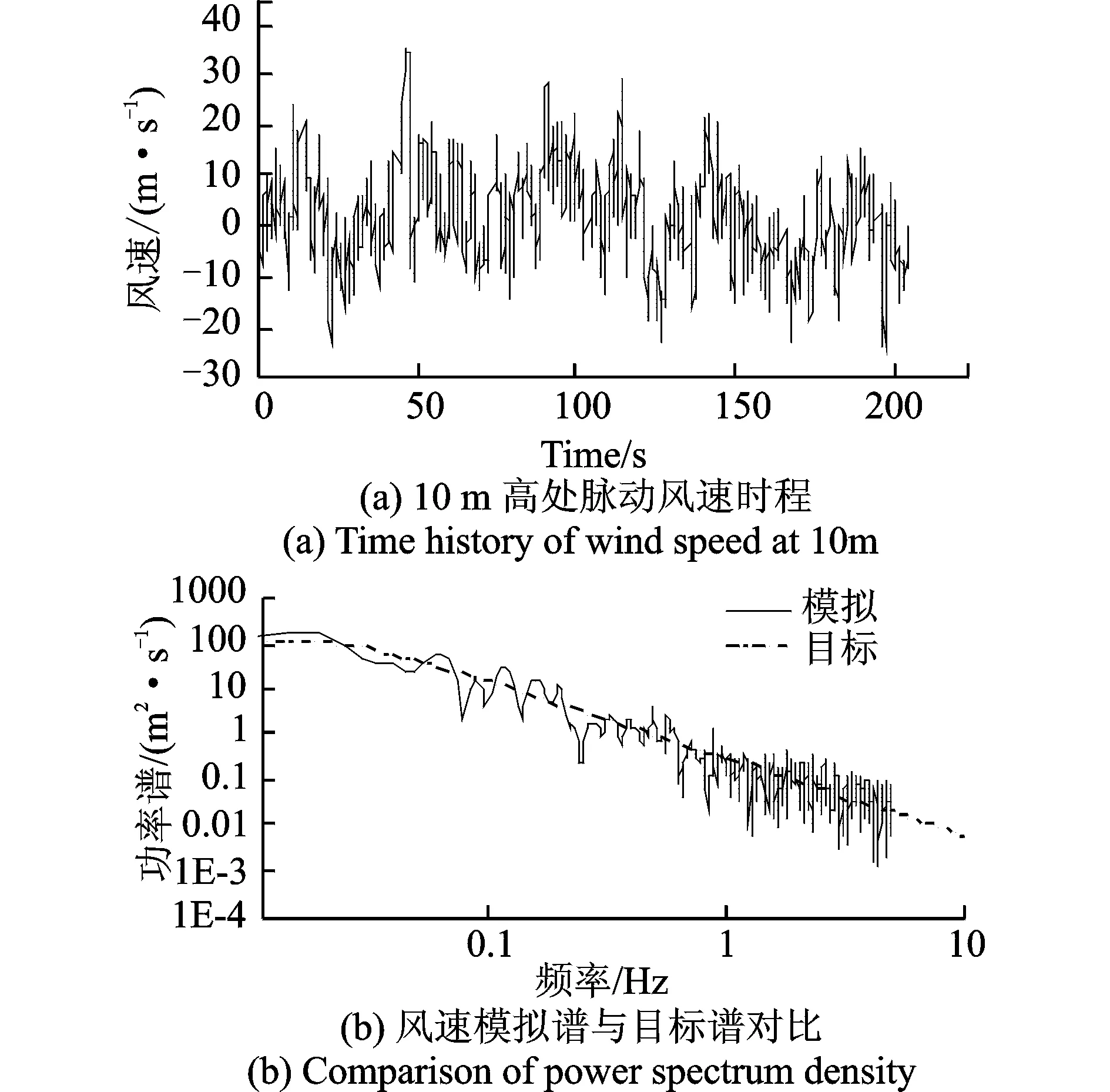
图7 10 m高处脉动风速时程及其模拟谱与目标谱对比Fig.7 Time history of fluctuating wind speed and power spectrum density

3 风载荷激励下NES振动控制算例

3.1 计算模型与等效简化

模拟风速点为10, 20,…,120 m高度处。取10 m高度处10年期平均风速值为36.3 m/s[12]。NES安装在结构的顶层中间位置，其沿轨道运动方向与顺风向风载荷施加的方向平行。仿真对象为一框架核心筒结构的32层120 m高建筑结构，结构平均层高3.6 m、宽45 m，平均每层质量为1854.5 t，结构弱轴向振动一阶模态质量17935 t。由于在有限元软件中无法直接对安装NES的结构进行风载荷计算，所以对使用ETABS建立的模型进行等效处理，仿真对象ETABS模型的平面图与立面图如图8所示。

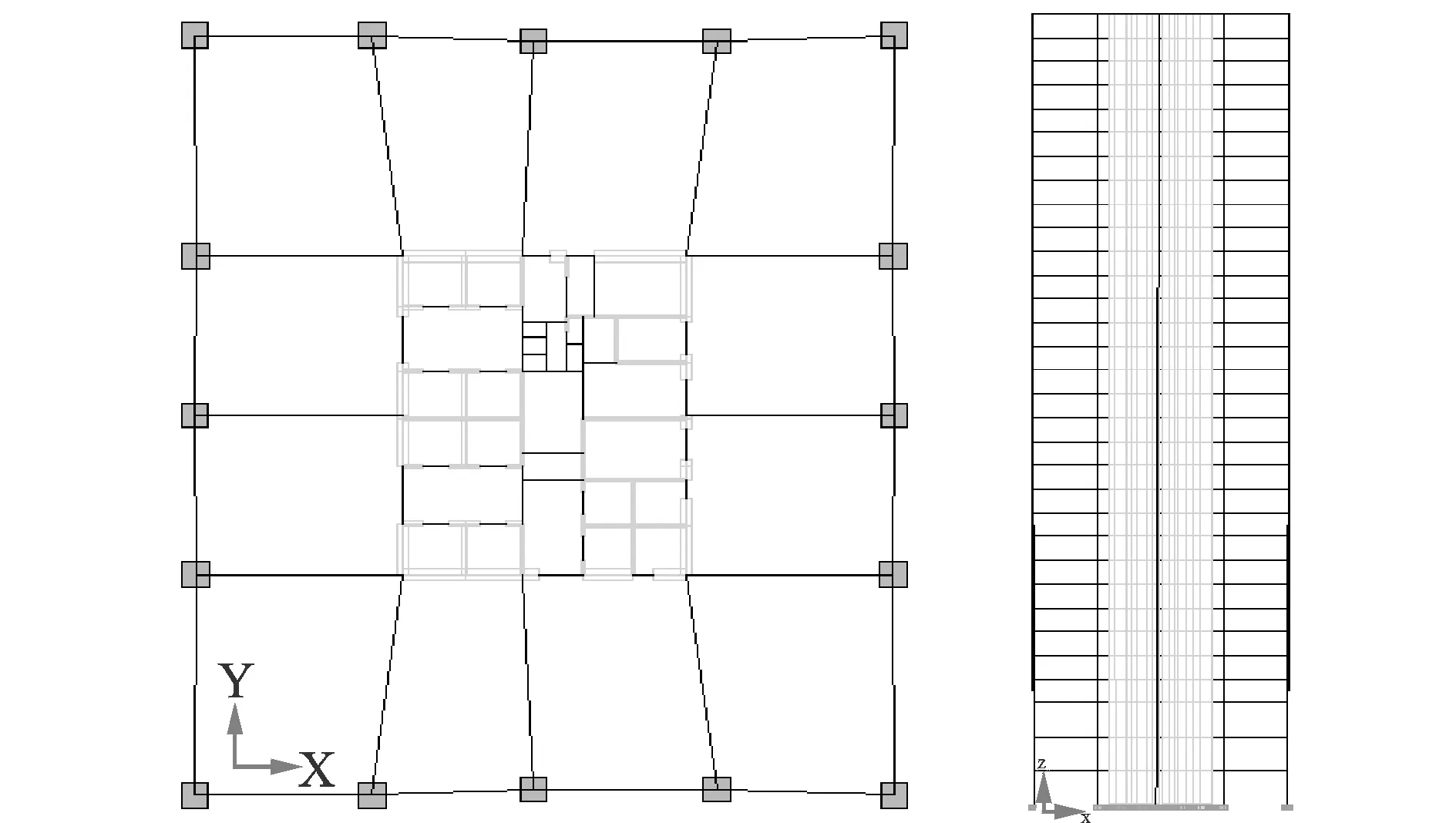
图8 结构ETABS模型的平面图与立面图Fig.8 Structure plan and elevation of ETABS model

对模型进行计算后选取弱轴向进行控制，使用文献[13-14]中的模型简化理论与计算方法建立弱轴向的集中质量串联多自由度模型。其弱轴向刚度矩阵通过以下步骤获得：对模型中第i层中各节点施加总和为一单位力的水平载荷，由各个节点在此载荷下的水平位移求出该层的名义位移，由此得到柔度系数。从而由柔度系数可以得到柔度矩阵，对柔度矩阵求逆得到侧向刚度矩阵。等效计算得到的弱轴向各阶振动的周期与ETABS中模型计算对应周期的对比如表3所示。将ETABS中计算得到的振型与简化之后的振型进行归一化处理之后，振型对比如图9所示。

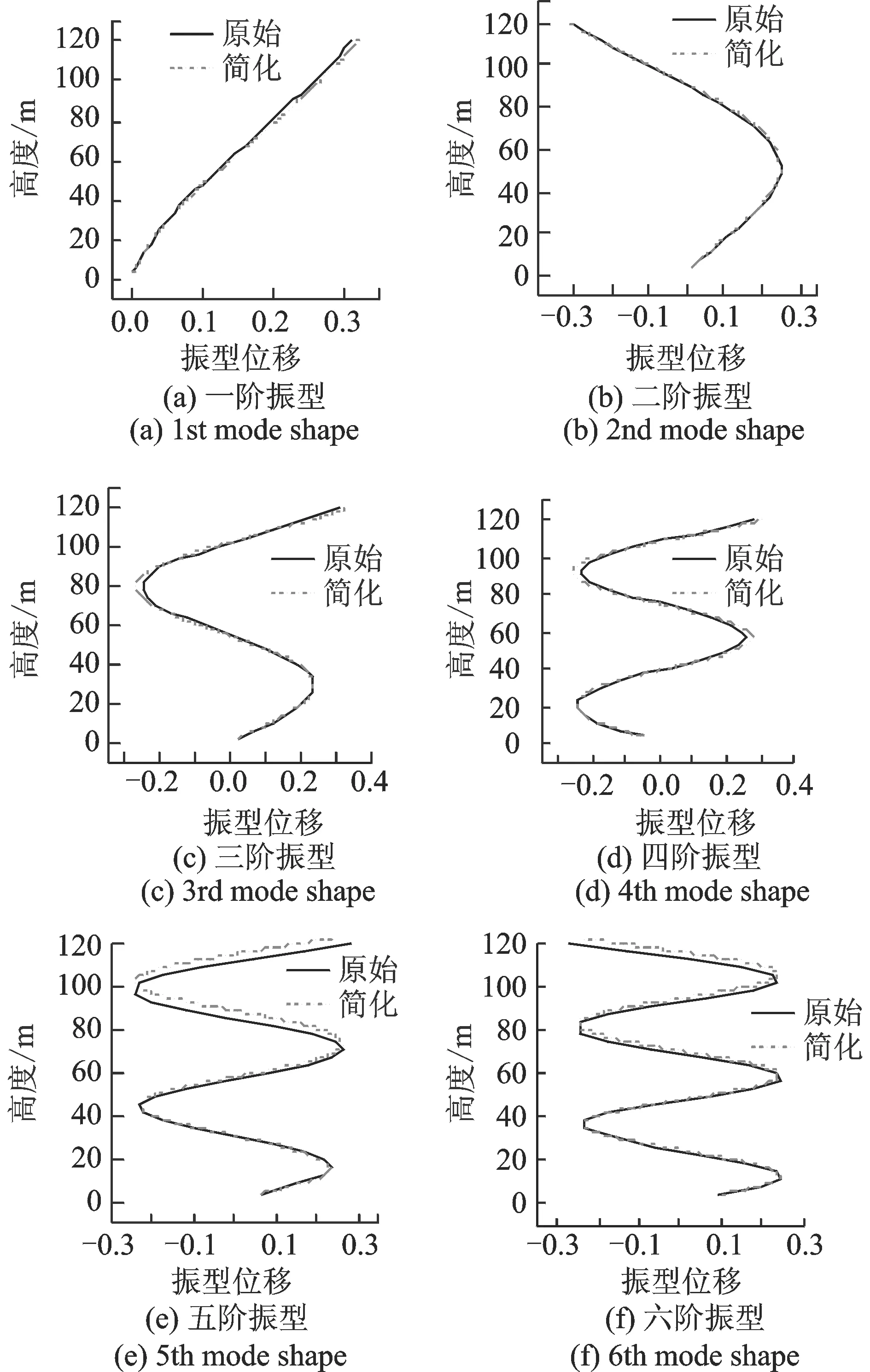
图9 结构弱轴向前六阶原始与简化模型振型对比Fig.9 Comparison of the first six vibration modes of weak axial

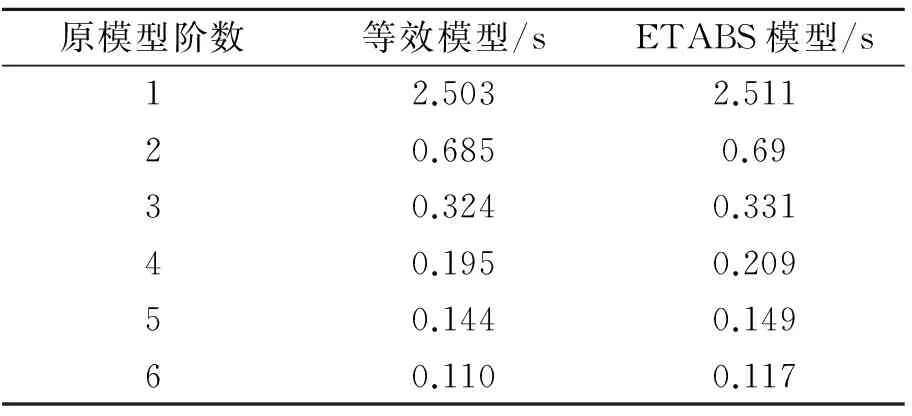
表3 弱轴向对应的6阶周期对比

结构简化之后的阻尼计算采用瑞利阻尼：

C=α·M+β·K

(10)

(11)

式中M为质量阵，K为刚度阵，ω1与ω2分别为结构的一阶、二阶频率，ξ为结构的阻尼比。本算例中结构的阻尼比取值0.05。

3.2 NES参数优化

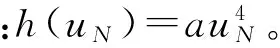
在上述优化方法的基础之上对NES的质量比、轨道表达式系数与阻尼参数进行计算。NES质量块的选择范围为结构1阶模态质量的1%～4%。在参数优化过程中，4个质量比对最大加速度的最佳控制效果如图10所示，在使用NES进行脉动风载荷作用下的结构振动控制时，质量比越大控制效果越好。但是随着质量比的增加控制效果的增加并不显著，并且质量比过大会给施工增加难度，在这里选取1%的质量比。

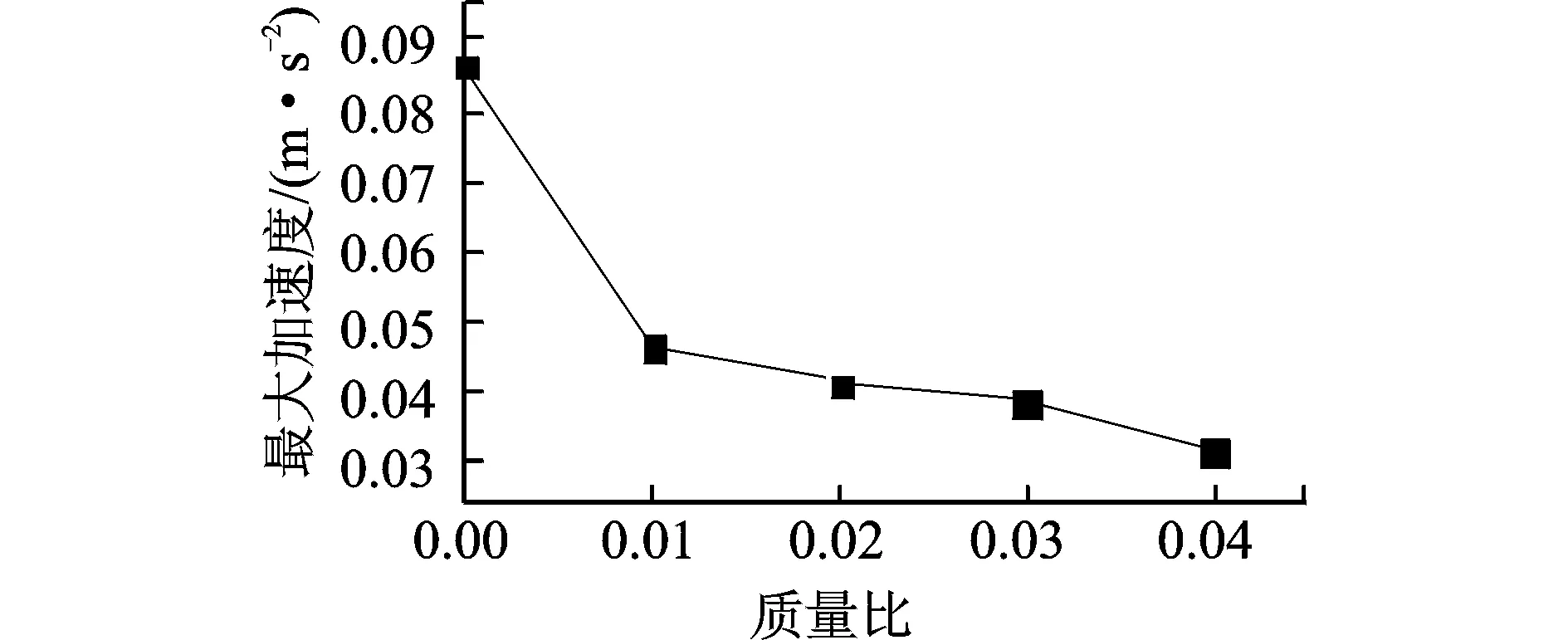
图10 不同质量比对最大加速度的控制Fig.10 The curve of control effect on maximum acceleration of different mass ratio

在寻找较优阻尼参数过程中把等效水平阻尼的范围限定在0.5～20 kN·m/s，进行计算并寻找其中的较优参数。在质量比1%、轨道系数0.9条件下，较优的等效水平阻尼系数为9 kN·m/s。在优化计算过程中，NES对结构顶层最大加速度的控制效果随阻尼的变化如图11(b)所示。从图中观察可以得出，最大加速度的控制并不需要很大的黏滞阻尼，随着阻尼的增大反而对最大加速度的控制变弱。

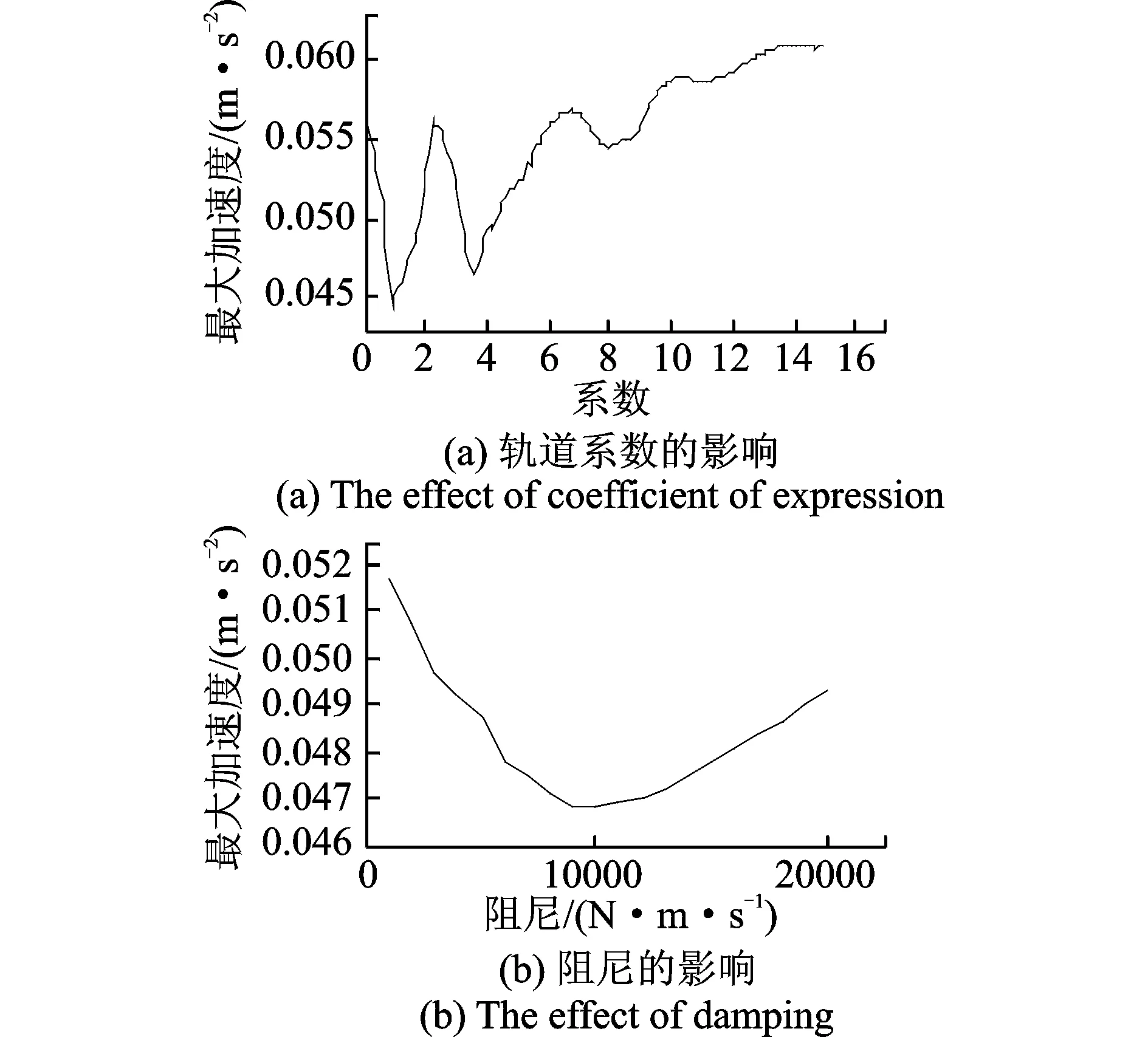
图11 不同轨道系数与阻尼对顶层最大加速度的控制Fig.11 The curve of control effect on maximum acceleration of roof at different coefficient and damping

3.3 计算结果

在模拟得到的风载荷作用下，计算得出仿真对象无NES控制状态下顶层的最大加速度为0.0866 m/s2,加速度均方根为0.0179。选取优化计算得到NES参数：质量比为1%、轨道系数0.9和等效水平阻尼9 kN·m/s，计算得仿真对象被NES控制状态下顶层的最大加速度为0.0467 m/s2、加速度均方根为0.0117。NES使脉动风载荷作用下的仿真对象结构顶层最大加速度降低46%，加速度均方根减小34.6%，有效地提高了建筑的舒适度。NES控制与无控状态下的顶层加速度时程数据对比如图12所示，结果可以较为直观地体现出控制的有效性。

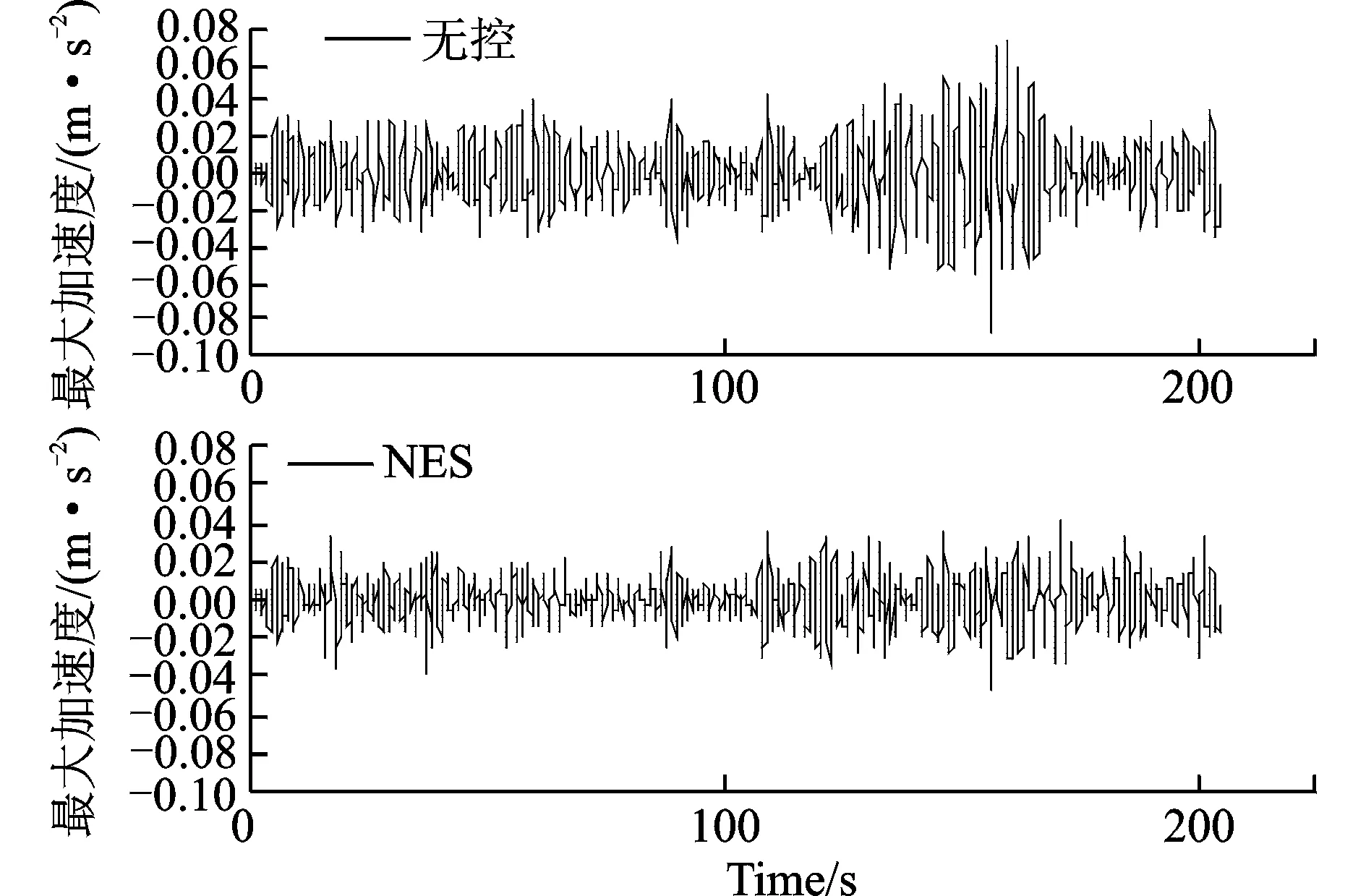
图12 顶层加速度时程对比Fig.12 Comparison of acceleration time history at roof of the frame uncontrolled and controlled by NES

将计算得到的脉动风载荷作用下结构顶层加速度信号进行小波变换之后得到各阶频率的能量时程，结构在风载荷作用下振动的一阶频率能量时程在无控与NES控制条件下的对比如图13(a)所示，二阶频率能量时程对比如图13(b)所示。从图中无控与有NES控制下顶层的加速度时程对比可以看出，NES对结构风载荷作用下的振动控制能同时作用于结构的多个固有频率范围。

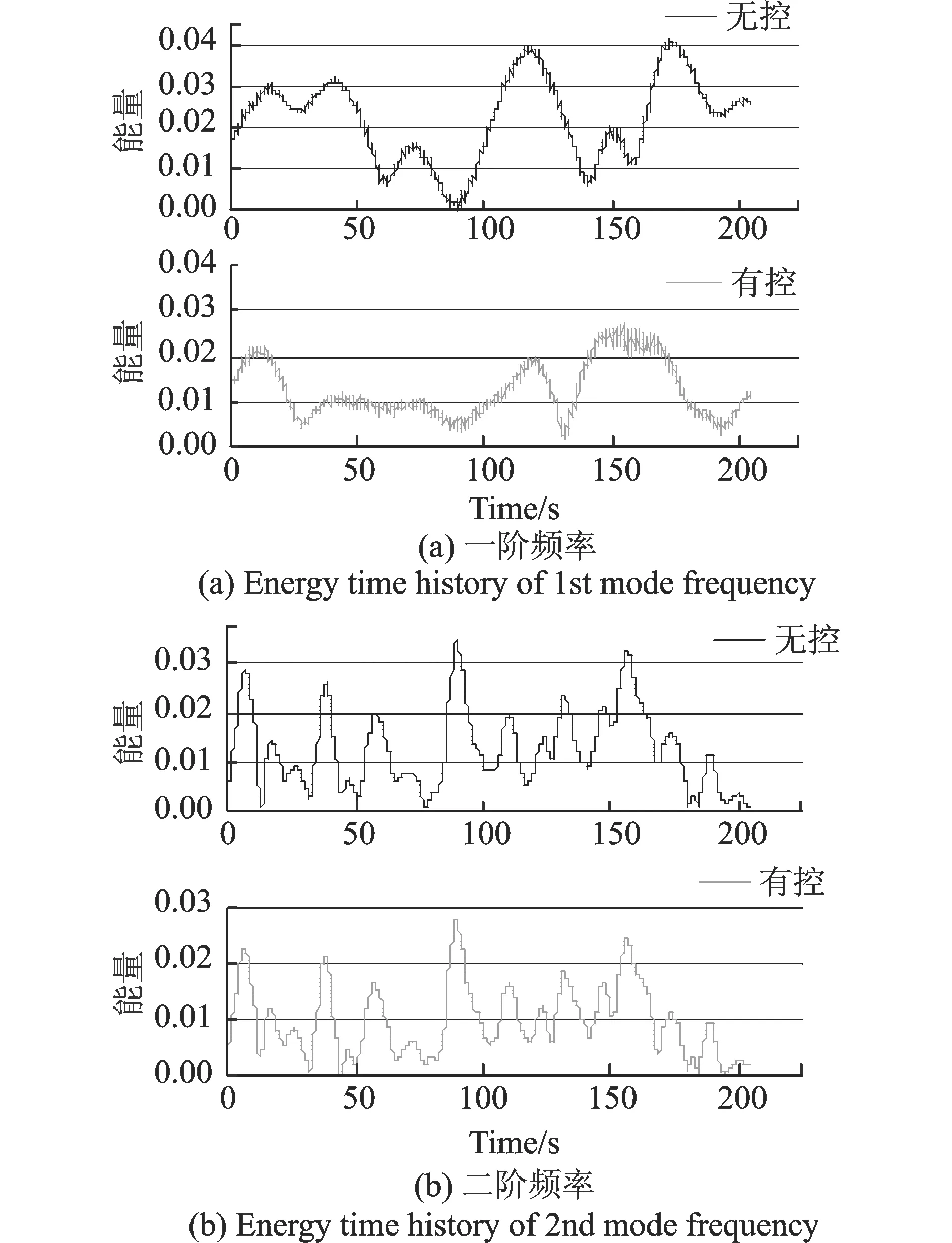
图13 频率能量时程对比Fig.13 Comparison of energy time history at first and second vibration frequency

4 结 论

本文介绍了被动式轨道型NES，并对其频率控制区间较宽的特性进行了实验研究。为了研究轨道型NES对建筑结构风致振动控制的应用，使用AR模型模拟出符合规范的不同高度相关脉动风速，将其作为外界激励加载到经过简化的建筑结构计算模型上。以结构顶层最大加速度为控制目标对轨道型NES的轨道表达式、质量比和阻尼参数进行了优化，选择较优参数进行仿真计算，根据计算结果得到以下的结论：NES对高层建筑结构风致振动的结构加速度响应有较好的控制效果；相对传统TMD而言，NES有着可以同时减小多个模态振动的优点；轨道型NES的振动效果不仅受轨道表达式的影响，而且还与其自身的阻尼参数紧密相关。

[1] Roberson R E. Synthesis of a nonlinear dynamic vibration absorber [J]. Journal of the Franklin Institute, 1952, 254(3): 205—220.

[2] Vakakis A F, Gendelman O. Energy pumping in nonlinear mechanical oscillators: part Ⅱ: resonance capture [J]. Journal of Applied Mechanics, 2001, 68(1): 42—48.

[3] Gourdon E, Lamarque C H. Energy pumping with various nonlinear structures: numerical evidences [J]. Nonlinear Dynamics, 2005, 40(3): 281—307.

[4] Vakakis A F. Inducing passive nonlinear energy sinks in vibrating systems [J]. Transactions-American Society of Mechanical Engineers， Journal of Vibration and Acoustics, 2001, 123(3): 324—332.

[5] Jiang X, Mcfarland D M, Bergman L A, et al. Steady state passive nonlinear energy pumping in coupled oscillators: theoretical and experimental results [J]. Nonlinear Dynamics, 2003, 33(1):87—102.

[6] Starosvetsky Y, Gendelman O. Attractors of harmonically forced linear oscillator with attached nonlinear energy sink II: optimization of a nonlinear vibration absorber [J]. Nonlinear Dynamics, 2008, 51:47—57.

[7] 张也弛,孔宪仁. 非线性耦合振子间产生靶能量传递的初始条件[J]. 哈尔滨工业大学学报,2012, 44(7):21—26.

Zhang Yechi, Kong Xianren. Initial conditions for targeted energy transfer in coupled nonlinear oscillators [J]. Journal of Harbin Institute of Technology, 2012, 44(7):21—26.

[8] Wang J, Wierschem N E, Spencer B F, et al. Track nonlinear energy sink for rapid response reduction in building structures [J]. Journal of Engineering Mechanics, 2015, 141(1), doi:10.1061/ ( ASCE ) EM. 1943-7889.0000824

[9] Vaurigaud B, Savadkoohi A T, Lamarque C H. Efficient targeted energy transfer with parallel nonlinear energy sinks: theory and experiment [J]. Journal of Computational and Nonlinear Dynamics, 2011, 6(4):1—10.

[10]刘章军,李杰. 脉动风速随机过程的正交展开[J]. 振动工程学报, 2008, 21(1): 96—101.

Liu Zhangjun, Li Jie. Orthogonal expansion of stochastic processes for wind velocity [J]. Journal of Vibration Engineering, 2008, 21(1): 96—101.

[11]张建胜,武岳,沈世钊. 不同脉动风相干函数对高层建筑风振响应的影响[J]. 振动工程学报, 2009, 22(2): 117—122.

Zhang Jiansheng, Wu Yue, Shen Shizhao. Wind-induced response of high-rise buildings analyzed by different coherence functions of gust [J]. Journal of Vibration Engineering, 2009, 22(2): 117—122.

[12]陈俊儒,吕西林. 上海中心大厦脉动风载荷模拟研究[J]. 力学季刊, 2010, 31(1): 92—100.

CHEN Junru, LU Xilin. Simulation of fluctuating wind load of Shanghai Center Tower [J]. Chinese Quarterly of Mechanics, 2010, 31(1): 92—100.

[13]滕军,幸厚冰. 京基100大厦AMD控制系统在线计算关键技术研究[J]. 振动与冲击, 2011, 30(11): 230—235.

Teng Jun, Xing Houbing. Study of key techniques of online algorithms for AMD control system used in KK100 [J]. Journal of Vibration and Shock, 2011, 30(11): 230—235.

[14]王文胜,徐胜利,程耿东. 基于简化模型的结构动力特性优化[J]. 工程力学, 2011, 28(12): 45—50.

Wang Wensheng, Xu Shengli, Cheng Gengdong. Optimization of structural dynamic characteristics based on the reduced model [J]. Engineering Mechanics, 2011, 28(12): 45—50.

Simulation of track nonlinear energy sink for wind-induced
vibration control in high-rise building

LIUZhong-po1,WUJian-zhong1，WANGJing-jing2,LÜXi-lin2

(1.School of Mechanical Engineering, Tongji University, Shanghai 201804, China;
2. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)

Track nonlinear energy sink (NES), a type of passive structural control device effective in a wide range of frequency, is introduced in the paper. Shaking table experimental investigation of a five-story frame structure coupled with a track NES are conducted by inputting white-noises. The results show that the track NES is capable of reducing the structural responses in multiple modes. NES can be applied to wind-induced vibration control of high-rise buildings due to this advantage. The AR linear regression method is applied to generate the wind velocity time histories at different heights. Under the wind excitations, parameters of a track NES including the mass, track express and damping, are optimized to reduce the acceleration responses of a high-rise building to which the track NES is attached. The simulated results show that with proper parameters, the track NES is able to attenuate the wind-induced vibration efficiently.

wind-vibration control； high rise building; fluctuating wind; NES; AR model

2015-10-20；

2016-06-21

国家自然科学基金重大研究计划重点国际合作项目(51261120377);国家自然科学基金重大研究计划集成项目(91315301-4)

TU311.3；TU352.2

：A

1004-4523(2016)06-1088-09

10.16385/j.cnki.issn.1004-4523.2016.06.019

刘中坡(1980—),男,博士研究生。电话:13166129768； E-mail:1110200@tongji.edu.cn

吕西林(1955—), 男，教授，博士生导师。电话：(021)65982666；E-mail：lxlst@tongji.edu.cn