含复杂声边界的圆柱壳结构声振特性研究①

王 威， 陈炉云

(1.武汉大学土木建筑工程学院，湖北 武汉 430072；2.上海交通大学海洋工程国家重点实验室，上海 200240)

含复杂声边界的圆柱壳结构声振特性研究①

王 威1， 陈炉云2

(1.武汉大学土木建筑工程学院，湖北 武汉 430072；2.上海交通大学海洋工程国家重点实验室，上海 200240)

对复杂声边界内的结构振动-声辐射问题开展了研究。针对同时存在着自由液面和刚性壁面的复杂声边界问题，结合镜像法原理，应用双反射方法推导了复杂声边界条件下的圆柱壳结构远场声压方程式。最后，以直角空间域内的圆柱壳结构为例，进行了结构的声振特性数值计算。在算例中，对比了声边界特性、频率及与声边界的距离对声辐射功率、声辐射指向性的影响。研究成果为解决含复杂声学边界的声振问题提供了参考。

声辐射； 圆柱壳； 双反射法； 复杂声边界

引 言

连续结构的振动噪声问题成为当前研究的一个热点。对于无界空间(自由声场)的结构声辐射问题，可通过直接求解 Helmholtz 声学方程来解决。然而，在实际的声学计算中需考虑各种声边界条件的影响。当前，很多的研究工作涉及到半空间域内的结构声辐射问题。Al-Khaleefi等[1]通过求解不同声边界条件的声格林函数解，分析声边界特性对结构-声辐射特性的影响。Liu等[2]应用边界积分方法对半空间域内的声辐射和声散射问题进行研究。邹元杰等[3-4]用镜像法探讨了半空间内辐射频率、声源位置及自由液面和刚性壁面对声振特性的影响。Seybert等[5]应用修正格林函数来消除无穷大边界积分问题，并将边界积分方程推广到四分之一空间域内。林皋等[6]给出了满足所有自由边界条件的半无限弹性空间域的Green函数解形式，并将边界元法推广到三维声振耦合问题中。Lu等[7]基于声格林函数，对海底的声反射问题进行研究，并对比水深对声辐射特性的影响。Bapat等[8]基于镜像理论，采用快速多点边界元法研究了三维半空间的声辐射问题。此外，为解决具有更为复杂声边界条件的结构-声辐射问题，陈炉云等[9]应用保角变换理论推导了具有组合边界任意夹角声域的声辐射问题，并研究直角空间域内点声源的声辐射功率、声指向性问题。Chan等[10]针对角域内的结构振动波的反射问题，应用双反射法对结构振动波进行求解。

圆柱壳结构广泛应用于航空航天、海洋工程等领域，对圆柱壳结构声振问题的研究具有重要的理论和实践意义。Hasheminejad等[11-12]应用镜像理论分析了半空间域内的圆柱壳结构声辐射问题。Shao等[13]针对圆柱壳结构的声辐射问题，利用复变函数和汉克尔函数将无限积分问题变成有限积分问题，提高了计算效率并保证了计算精度。刘佩等[14]对有限深水域中的底部边界对圆柱壳声振特性的影响进行研究，同时对比分析了静水压力对声辐射特性的影响。陈美霞等[15]将环肋、舱壁等构件定义为系统的子结构并用圆环板模型进行处理，在此基础上根据变形协调条件将其组装在总模型中，最后应用波动法对加肋圆柱壳结构的振动问题进行了求解。对于复杂边界条件下的圆柱壳结构声振问题，叶文兵等[16，17]推导了含自由液面和刚性面的组合边界下的圆柱壳结构声辐射方程，但在其研究中没有考虑自由液面与刚性面交界处的影响，同时假设边界处不存在二次反射。

文章针对含复杂边界的圆柱壳结构声振问题，通过引入双反射理论，推导了同时具有自由液面和刚性面的圆柱壳结构声辐射方程。最后，分析边界特性、辐射频率和位置对声辐射功率和声指向性的影响。

1 圆柱壳结构声振方程

如图1所示为处于自由声场的圆柱壳结构的声振系统，以z，θ和r分别表示壳体的轴向、周向和径向方向建立柱坐标系统。以u(z,θ)，v(z,θ)和w(z,θ)分别表示圆柱壳结构壳体的中面轴向、周向和径向位移。

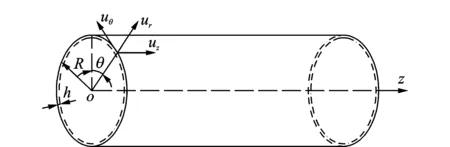
图1 圆柱壳体坐标系Fig.1 Schematic of the system for cylindrical shell

在图1中，壳体为薄壳结构，其厚度为t且满足t/R≪1、中面半径为R、结构材料密度为ρ，材料弹性模量为E，材料泊松比为μ。

1.1 圆柱壳动力响应方程

设圆柱壳结构为无限长薄壳结构，基于Flügge圆柱壳薄壳理论，将中面位移展开为与壳体的轴向波数有关的函数形式，此时圆柱壳轴向、环向和径向位移函数可分别写为：

(1a)

(1b)

(1c)

式中n为展开系数，系数Un(kz)，Vn(kz)和Wn(kz)分别为波数域下的轴向、周向和径向的位移幅值，kz为轴向波数。

1.2 圆柱壳声辐射方程

连续结构的稳态振动将在理想流体介质中引起的小振幅声波，其声压方程满足如下波动方程和边界条件：

▽2p(r,θ,z)+k2p(r,θ,z)=0

(2)

(3)

式中 ▽2为拉普拉斯算子，k=ω/c为波数、ω为圆频率、c为声速。在柱坐标系下，自由声场的圆柱壳结构的远场辐射声压方程可写成如下形式

(4)

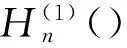
2 复杂边界下圆柱壳声压方程

复杂的声域空间通常包括一种或多种边界条件，如结构边界、刚性反射面、自由液面等等。对于水中的圆柱壳结构，在特定的情况下，可能同时存在自由液面和刚性壁面的情况，由于受多种类型的边界条件的影响，这种声边界条件下的水下圆柱壳结构的声振特性必然有其独特性。如潜艇位于码头附近与潜艇位于浅水中的声振问题都可抽象成这种情况。基于此理念，文章对三维空间内含复杂边界的圆柱壳声振特性进行研究，并分析其结构声辐射功率和声指向性。

2.1 复杂边界模型

设无限长圆柱壳结构处于自由液面和刚性壁面边界所组成的直角空间域内，如图2所示。以圆柱壳结构的中心为原点建立坐标系，定义z坐标为圆柱壳的轴向方向。x轴正方向向下，y轴正方向向右。圆柱壳中心与刚性壁面以及自由液面之间的距离分别为l和s，并满足(l>R，s>R)，其中R为圆柱壳结构半径。

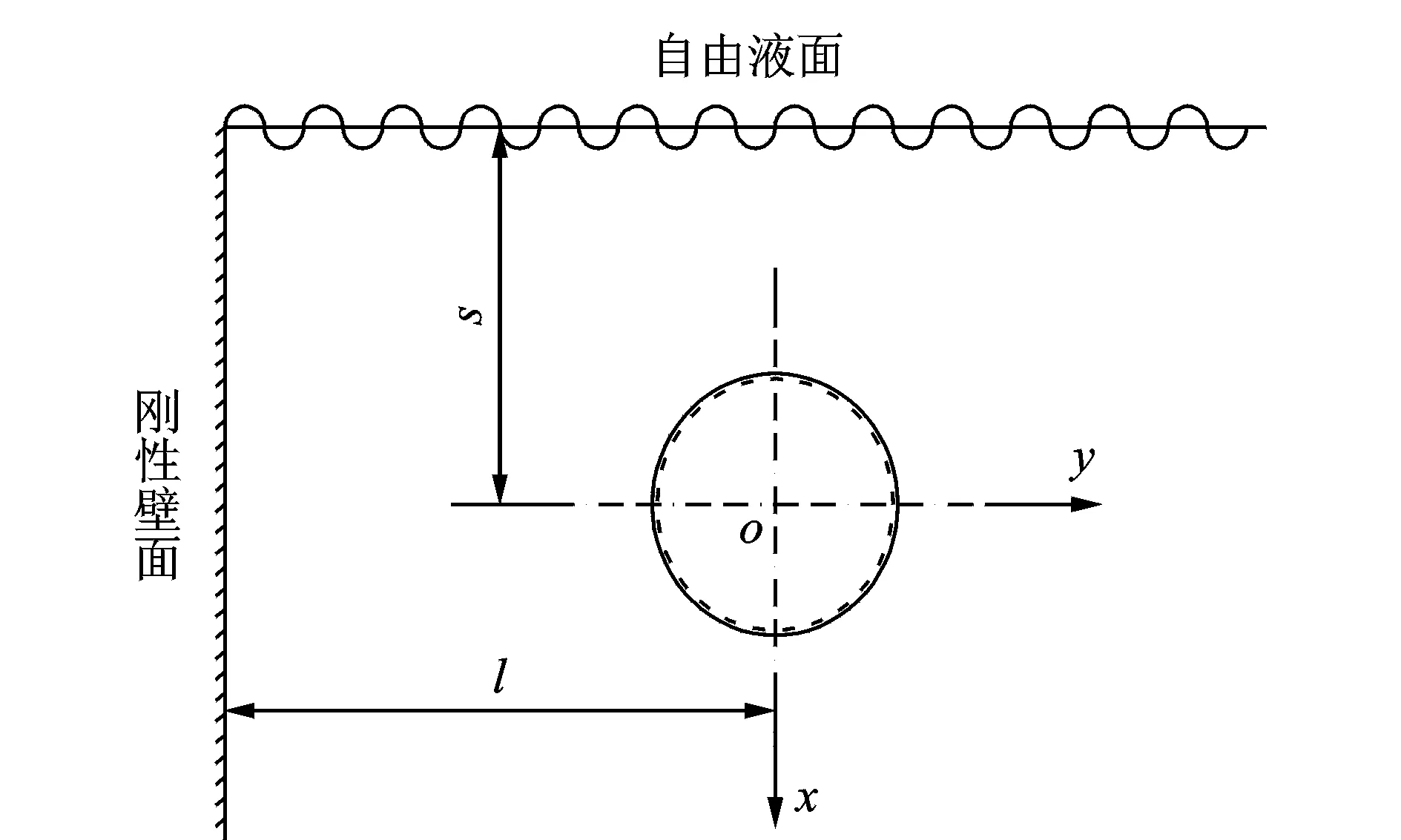
图2 复杂声边界下圆柱壳结构模型Fig.2 Complex acoustic boundary of cylindrical shell

在文献[16-17]中，研究了具有组合声边界的圆柱壳结构声辐射问题，但在该文中没有考虑二次反射问题。

对于这种含复杂声边界的声辐射问题，由于同时存在着刚性壁面和自由液面，此时在两个声边界的交界处将不能用单一的刚性壁面及自由液面特性来描述。此时，为解决交界处的影响，需要用双反射理论来解决。

图3所示为直角域内的双反射模型。

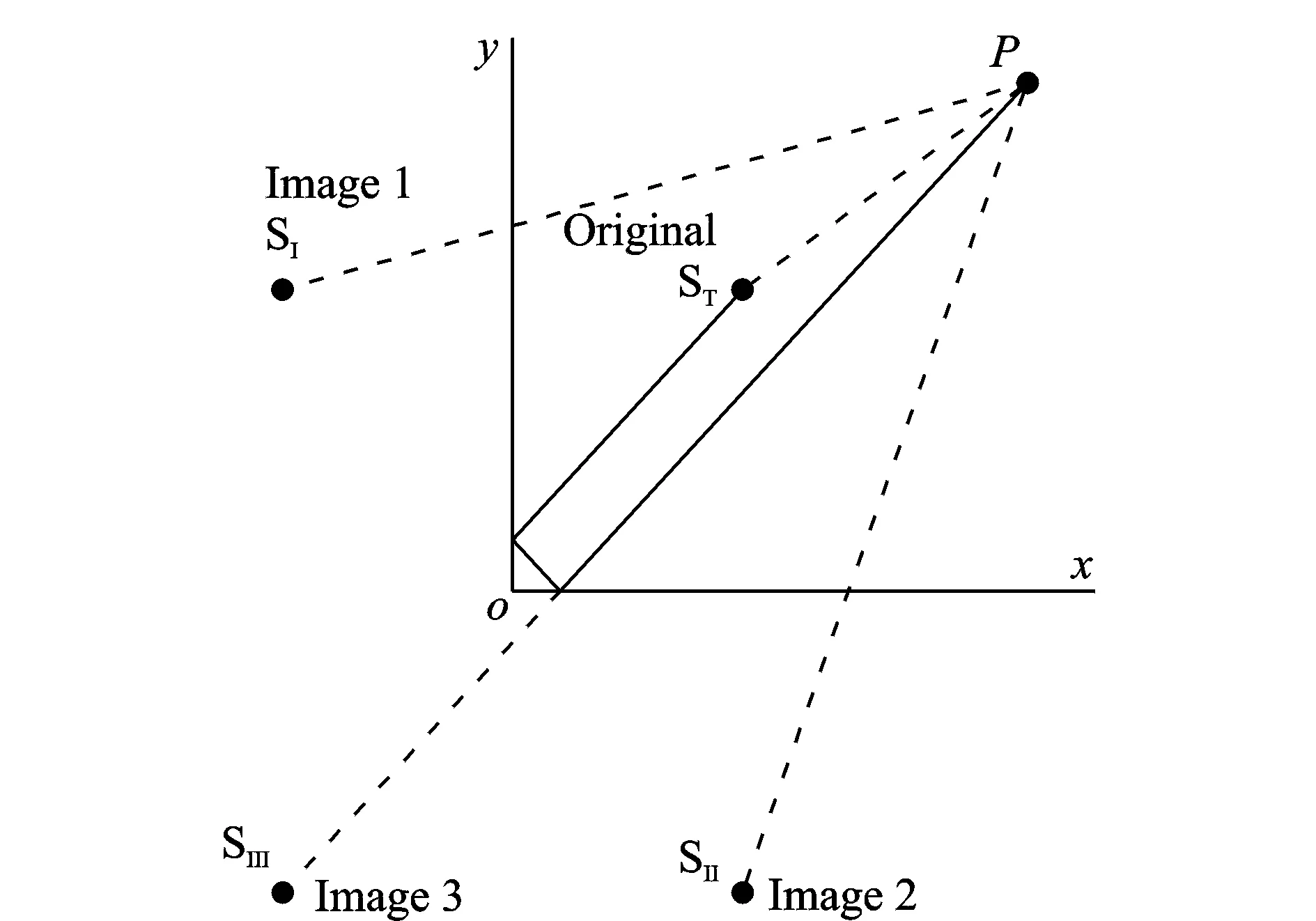
图3 直角域内双反射模型Fig.3 Double reflection method in quarter-infinite domain

在图3中，ox和oy为直角域内的两个声边界。Original 为实际声源，Image1和Image2分别为通过边界oy和ox镜像获得的“像声源”，而Image3为由双反射而获得的“像声源”。

2.2 复杂边界下圆柱壳声压方程

根据双反射理论，可得到如图4所示的复杂声边界下的圆柱壳结构声辐射示意图。图4中，P点为声场中任意参考点、实线环oT为真实圆柱壳结构、虚线环o1为因自由液面存在而形成的镜像、o2为因刚性壁面存在而形成的镜像、o3为因双反射而形成的镜像。在声场中，声波在刚性壁面上发生全反射(表面法向速度为零)，在自由液面处声压为零。

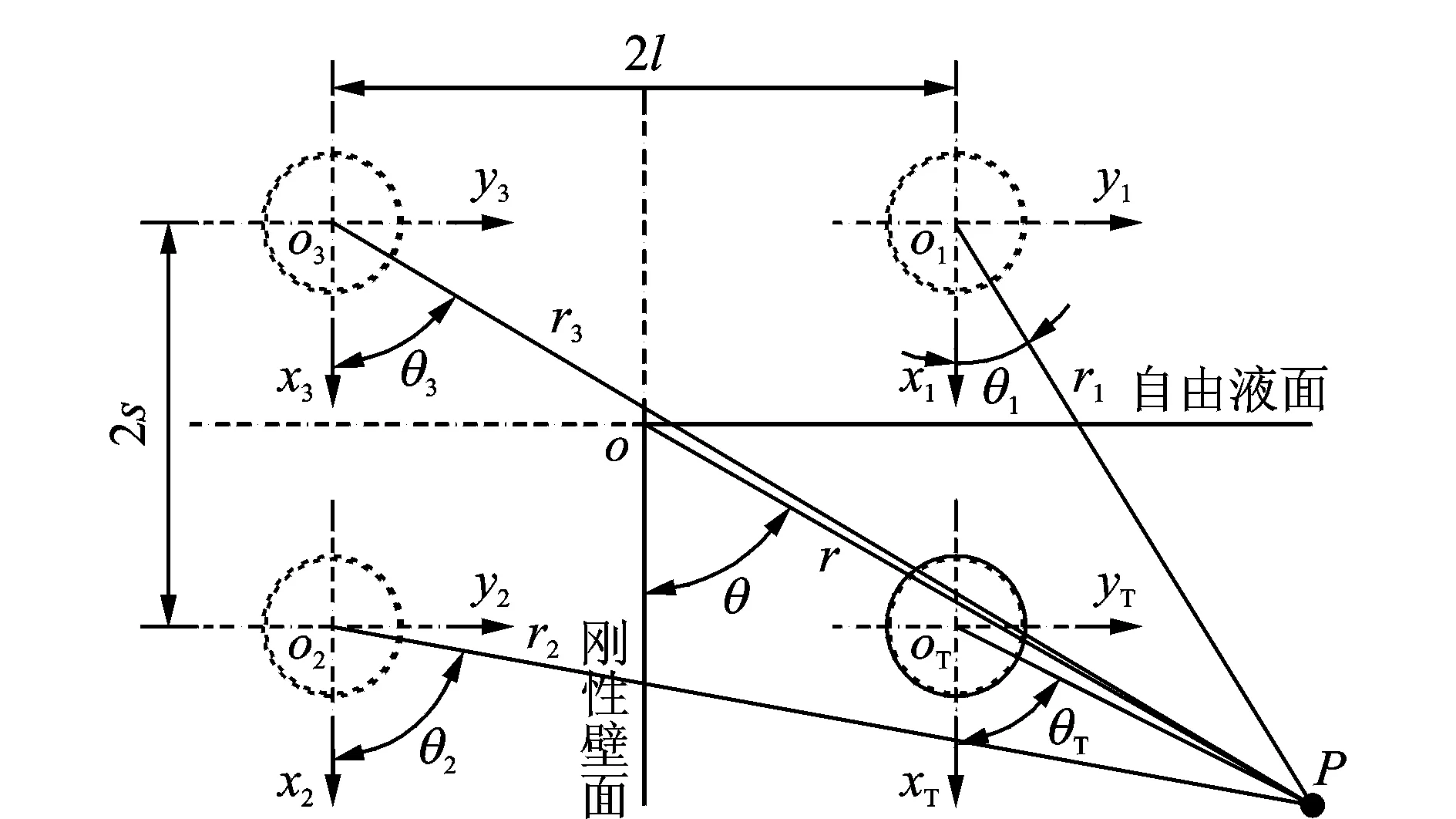
图4 复杂边界下的镜像图Fig.4 The image method in complex boundary

由于存在着3个镜像声源，对于声场空间上的任意参考点P，其声压值为p(r,θ,z)可由4部分叠加而成：

p(r,θ,z)=pT(rT,θT,zT)+p1(r1,θ1,z1)+

p2(r2,θ2,z2)+p3(r3,θ3,z3)

(5)

式中pT(rT,θT,zT)是真实柱面波在P点的辐射声压，p1(r1,θ1,z1)是以自由液面为对称面的镜像声源柱面波在P点的辐射声压，p2(r2,θ2,z2)是以刚性壁面为对称面的镜像声源柱面波在P点的辐射声压，p3(r3,θ3,z3)为双反射形成的镜像声源柱面波在P点的辐射声压。

3 复杂边界下的圆柱壳声辐射特性

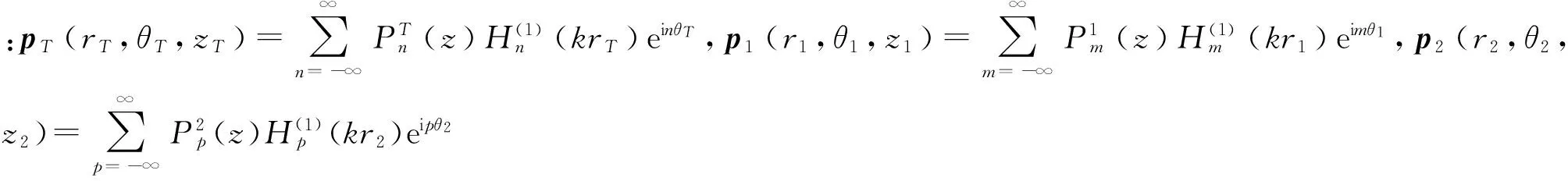
3.1 自由液面镜像

在自由液面处的声压为零，此时自由液面任意点(rT=r1=RT，θT=π-θ1)处的声压方程满足

(6)

将式(6)进行正交化处理，可写成如下形式

(7)

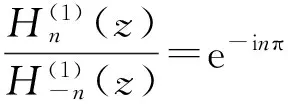
(8)

式中J()为第一类贝塞尔函数。

3.2 刚性壁面镜像

在刚性壁面处的法向振速为零，此时刚性壁面上的任意点(rT=r2=RT，θT=π-θ2)的声压方程满足：

(10)

式中J()为第一类贝塞尔函数。

3.3 双反射镜像

根据波的双反射理论，在自由液面和刚性壁面的交界处(图3中通过点o的线)的声压为零，在o点(rT=r3=RT，θT=π-θ3)处的声压方程满足

(11)

(12)

式中J()为第一类贝塞尔函数。

3.4 声辐射方程

结合公式(5)，(8)，(10)和(12)，可获得声场中具有复杂边界的圆柱壳结构远场声辐射方程为

(13)

对于式(13)的物理解释如下：根据圆柱壳结构及其镜像分布的对称性特点，真实圆柱壳结构和3个镜像圆柱壳结构的柱形声波到达刚性壁面上任意一点时，法向合成速度为零；同时，在自由液面上的声压为0。根据声波动方程解的唯一性原理，式(13)满足波动方程，因而式(13)是图2所叙述问题的唯一正确解。通过进一步的研究表明，当直角空间域的两个边界都为自由液面或刚性壁面情况下时，应用双反射法也可获得相应的解析解，对于这两种情况文中不进行展开叙述。

式(13)与文献[16]所描述的声压方程表达式相比，增加了声压项p3(r3,θ3,z3)，因而在理论和计算结果都与文献[16]的结果有重大的差异。

根据式(13)所描述的声辐射方程，可进行场点P的声压和声功率计算。定义4个圆环的中心点o为坐标系的原点，建立坐标系统为(r,θ,z)，其声压方程如下

(14)

4 含复杂边界的圆柱壳声辐射方程

4.1 圆柱壳声辐射功率

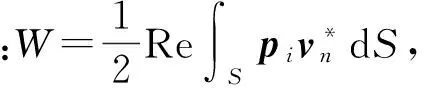
4.2 复杂边界下圆柱壳声指向性分析

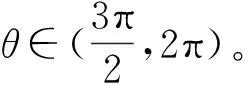
(15)

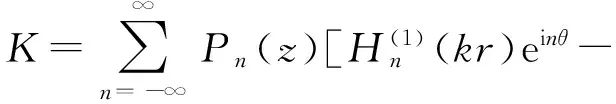
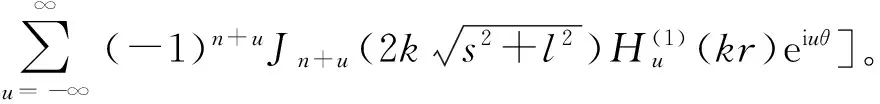
根据式(14)，(15)以及声辐射功率函数，即可计算出具有复杂边界特性的圆柱壳结构在流场中声辐射功率与声指向性。

5 数值分析和讨论

在数值计算中，对比圆柱壳结构位置、辐射频率等参数对圆柱壳声辐射功率和指向性的影响。

5.1 模型概述

在上述推导中，定义圆柱壳为无限长圆柱壳。在实际工程中，如有L≫l,s,r,R，则此时圆柱壳两端对结构声辐射的影响可以用两端存在两个无限大声障板，声学空间在[0，L]以内。

圆柱壳结构基本参数为：圆柱壳直径D=1 m; 圆柱壳长度L=50 m;壳板厚t=0.01 m。结构材料为钢，其力学特性为：密度ρ=7800 kg/m3；弹性模量E=210 GPa；泊松比μ=0.3。

声介质为水，声速c=1500 m/s，密度ρ=1000 kg/m3，声功率参考值：W0=1×10-12W。

设圆柱壳结构的表面运动为脉动运动，即结构表面速度幅值为一定值，其大小为 1.0 m/s。

圆柱壳结构中心与自由液面和刚性壁面之间的距离分别为s和l。分别以l=2.0 m，s=2.0 m；l=2.0 m，s=5.0 m；l=5.0 m，s=2.0 m；l=5.0 m，s=5.0 m共4种情况进行圆柱壳结构声辐射和声指向性对比分析。在计算中，频率段范围在0～800 Hz之间。在计算中的频率步长为2 Hz。

5.2 声功率对比分析

图5所示为圆柱壳结构位于流场中的不同位置处的声辐射功率对比图。

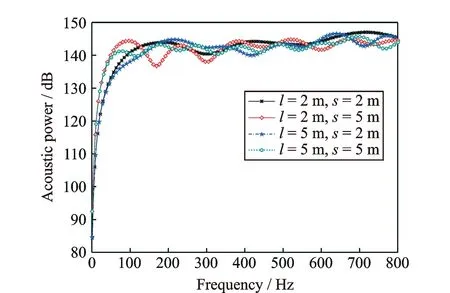
图5 声功率对比图Fig.5 The acoustic power comparison

由图4中的具有不同频率和与位置对声功率的影响可知：在低频段，与自由液面的距离对圆柱壳结构声辐射功率削减作用敏感，随着频率增加削减作用逐渐减弱。

5.3 声指向性对比分析

在圆柱壳结构指向性函数中，由于包含了场点P的距离参数r。在数值计算中，定义参数r=100 m，它描述了r=100 m的场点声压相对值，并将其定义成声压指向性参数。计算频率分别为100，200，400和800 Hz四种工况。声辐射指向性图如图6～9所示。

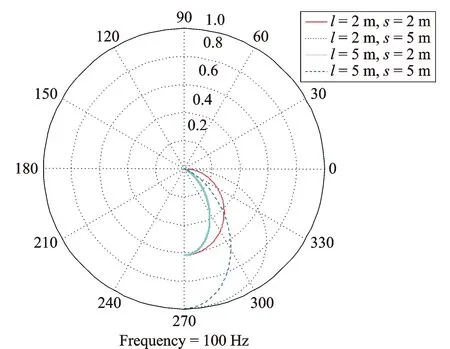
图6 声指向性对比图(100 Hz)Fig.6 The acoustic direction comparison (100 Hz)

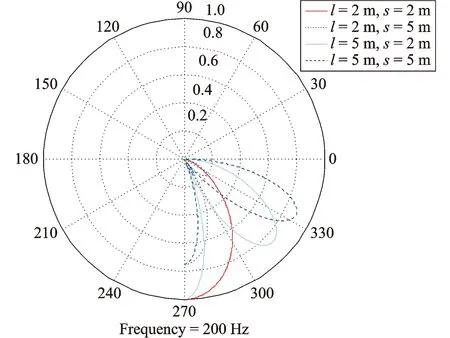
图7 声指向性对比图(200 Hz)Fig.7 The acoustic direction comparison (200 Hz)

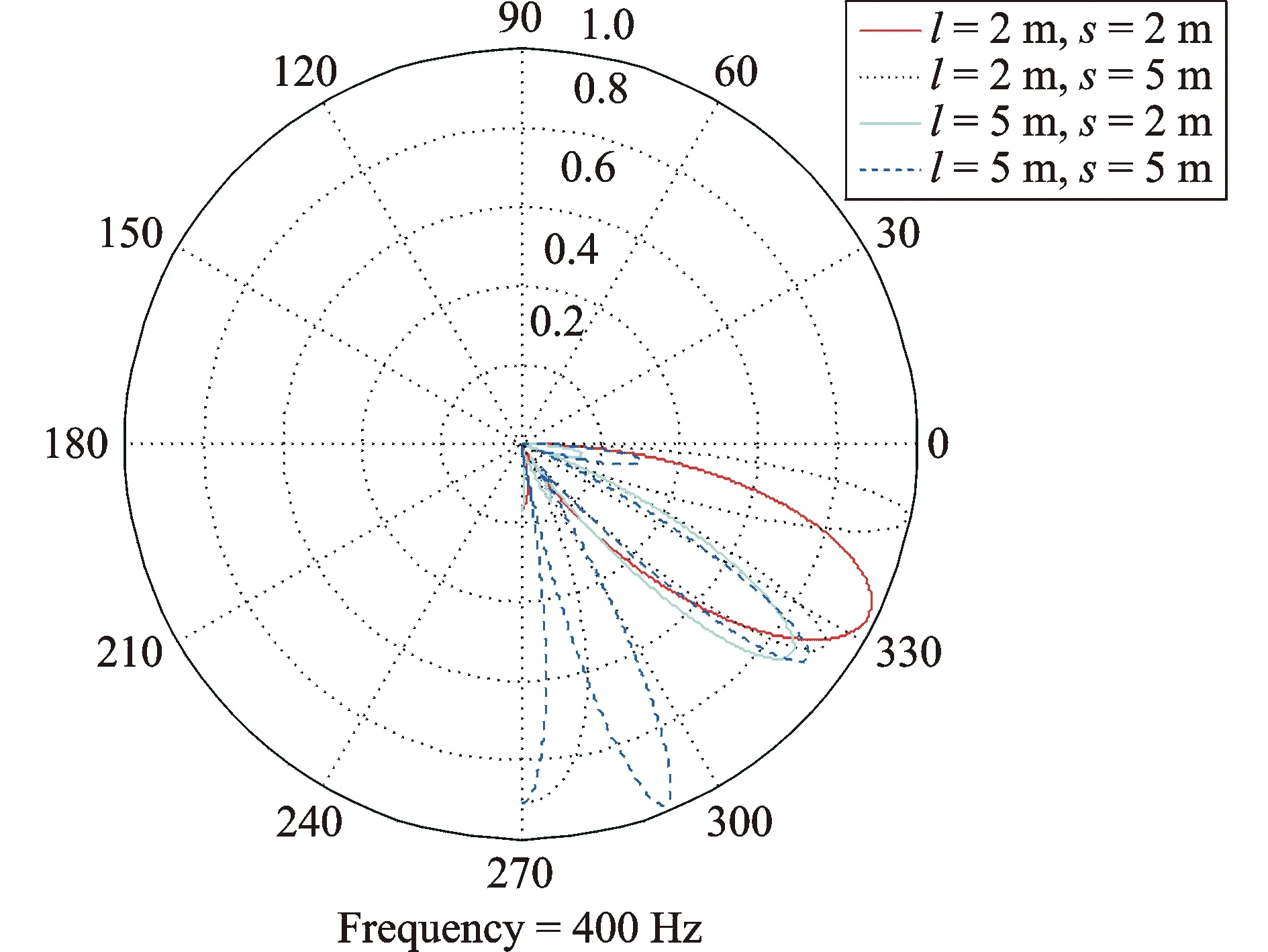
图8 声指向性对比图(400 Hz)Fig.8 The acoustic direction comparison (400 Hz)

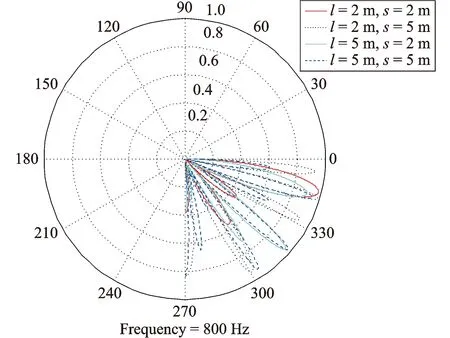
图9 声指向性对比图(800 Hz)Fig.9 The acoustic direction comparison (800 Hz)

对比图6～9中具有不同频率与位置参数对声辐射指向性的影响可知:

(1)在低频段时，圆柱壳结构与边界距离对指向性影响不是很明显，且主要指向为x正方向。

(2)在高频段时，与自由液面的距离对指向性影响很大，随着频率的增加表现得更为明显。

6 结 论

本文应用双反射理论结合镜像方法，获得了同时具有自由液面和刚性壁面边界的圆柱壳结构的声辐射方程。最后，通过数值计算对比位置、频率对声功率和声辐射指向性的影响。计算表明：在低频段与自由液面的距离对圆柱壳结构声辐射功率削减作用敏感；在高频段时，与自由液面的距离对指向性影响很大。研究成果可为进一步分析复杂受控声域内的结构声学特性提供参考。

[1] Al-Khaleefi A M, Ali A, Rajakumar C, et al. Acoustic analysis with absorbing finite elements and far-field computations using free-space Green′s functions[J]. Engineering Analysis with Boundary Elements, 2002, 26 (10):929—937.

[2] Liu J Y, Huang C F. Acoustic plane-wave reflection from a rough surface over a random fluid half-space[J]. Ocean Engineering, 2001, 28 (7):751—762.

[3] 邹元杰,赵德有,黎胜.自由液面和刚性壁面对结构振动声辐射的影响[J].声学学报,2005,30(1):89—96.

Zou Yuanjie, Zhao Deyou, Li Sheng. Impact of soft surface and hard plane on structural vibration and acoustic radiation[J].ACTA Acustica, 2005, 30(1):89—96.

[4] 邹元杰,赵德有.结构在浅水中的振动和声辐射特性研究[J].振动工程学报,2004,17(3):269—274.

Zou Yuanjie, Zhao Deyou. A vibro-acoustic study on structures in shallow water[J]. Journal of Vibration Engineering, 2004, 17(3):269—274.

[5] Seybert A F, Wu T W. Modified Helmholtz integral equation for bodies sitting on an infinite plane[J]. Journal of the Acoustical Society of America, 1988, 85(1): 19—23.

[6] 林皋,李炳奇,申爱国.半无限弹性空间域内点加振格林函数的计算[J].力学学报, 1994, 5(26): 583—592.

Lin Gao, Li Bingqi, Shen Aiguo. Evaluation of Green′s function for a point dynamic load in the interior of an elastic half-space[J].ACTA Mechanica Sinica, 1994, 5(26): 583—592.

[7] Lu J F, Jeng D S. Green′s function for a harmonic acoustic point source within seawater overlying a saturated poroelastic seabed[J]. Journal of Sound and Vibration, 2007, 307 (1-2): 172—186.

[8] Bapat M, Shen S L, Liu J Y. Adaptive fast multipole boundary element method for three-dimensional half-space acoustic wave problems[J]. Engineering Analysis with Boundary Elements, 2009, 33 (8-9):1113—1123.

[9] Chen Luyun, Zhang Yufang. Acoustic radiation analysis based on essential solution of Green′s Function[J].Journal of Shanghai Jiaotong University, 2013, 18(4):409—417.

[10]Chan K L, Smith B, Wester E. Flexural wave scattering in a quarter-infinite thin plate with circular scatterers[J]. International Journal of Solids and Structures, 2009, 46 (20):3669—3676.

[11]Hasheminejad S M, Azarpeyvand M. Modal vibrations of a cylindrical radiator over an impedance plane[J]. Journal of Sound and Vibration, 2004, 278 (3):461—477.

[12]Hasheminejad S M, Azarpeyvand M. Modal vibrations of an infinite cylinder in an acoustic half space[J]. International Journal of Engineering Science, 2003, 41 (19):2253—2271.

[13]Shao W, Mechefske C K. Acoustic analysis of a finite cylindrical duct based on Green′s functions[J]. Journal of Sound and Vibration, 2005, 287 (4-5):979—988.

[14]刘佩,刘书文,黎胜.潜深对水下圆柱壳振动声辐射特性的影响[J]. 舰船科学技术,2014,36(5): 36—41.

Liu Pei, Liu Shuwen, Li Sheng. The effects of immersion depth of submerged cylindrical shell on vibro-acoustic characteristics[J]. Ship Science and Technology, 2014, 36(5):36—41.

[15]陈美霞,谢坤,魏建辉.多舱段圆柱壳振动特性研究[J].振动工程学报,2014,27(4):555—564.

Chen Meixia, Xie Kun, Wei Jianhui. Vibration characteristics of multiple cabins of cylindrical shell[J]. Journal of Vibration Engineering, 2014, 27(4):555—564.

[16]Ye Wenbing, Li Tianyun, Zhu Xiang. The vibro-acousitc characteristics of the cylindrical shell partially submerged in the fluid[J].Applied Mechanics and Materials, 2012, 170-173: 2303—2311.

[17]叶文兵.潜浮状态下圆柱壳结构的声振特性研究[D].武汉：华中科技大学,2012.

Ye Wenbing. The Vibro-acoustic characteristics of cylindrical shells in the state of immersion and floating[D]. Wuhan: Huazhong University of Science and Technology, 2012.

Vibro-acoustic characteristics of cylindrical shells with
complex acoustic boundary conditions

WANGWei1,CHENLu-yun2

(1. School of Civil Engineering, Wuhan University, Wuhan 430072, China;
2. State Key Laboratory of Ocean Engineering, Shanghai Jiaotong University, Shanghai 200240, China)

The structural vibro-acoustic problem with complex acoustic boundaries is studied in this paper. According to the characteristic of acoustic boundary condition which combination free interface and rigid wall interface at the same time, the double reflection method and mirror image method are applied, and the expression function of the acoustic radiation function for the cylindrical shell structure is derived. Finally, the acoustic radiation characteristics of an infinite cylindrical shell structural in a quarter-infinite domain and numerical simulations are compared to illustrate the effects of the acoustic boundary characteristic, location, and radiation frequency on acoustic radiation power and acoustic radiation directivity. This study provides a new method to analyze the acoustic radiation problem with complex boundaries.

acoustic radiation; cylindrical shells; double reflection method; complex acoustic boundaries

2015-09-30；

2016-04-13

海洋工程国家重点实验室研究基金资助项目(1507)

TB532； O327

1004-4523(2016)06-1034-07

10.16385/j.cnki.issn.1004-4523.2016.06.012

王威(1975—)，男，高级工程师。电话: 13808636644;E-mail: 1841666106@qq.com

陈炉云(1975—)，男，助理研究员。电话: 13681708619;E-mail:cluyun@sjtu.edu.cn