带有支承间隙的压力管道振动非线性动力学行为研究①

唐千升， 李朝峰， 闻邦椿

(东北大学机械工程与自动化学院， 辽宁 沈阳 110819)

带有支承间隙的压力管道振动非线性动力学行为研究①

唐千升， 李朝峰， 闻邦椿

(东北大学机械工程与自动化学院， 辽宁 沈阳 110819)

以现代非线性动力学和Sanders薄壳理论为基础，建立了一端带有支承间隙的压力管道的非线性动力学模型，利用Ritz法对模型进行分析。针对非线性系统的具体特点，通过数值计算，得到管壁振动的幅频特性曲线，并研究了支承刚度和支承间隙对管道动力学特性的影响。结果表明：一端带有支承间隙的压力管道的管壁振动幅频曲线呈现出明显的非线性特征。支承间隙和支承刚度对管壁振动响应的各次谐波，尤其是低阶谐波的共振幅值和共振频率有着显著的影响。了解带有支承间隙的压力管道振动非线性动力学行为对管道的设计、安装和日常维护检查工作有着重要的意义。

非线性振动； 压力管道； 间隙模型； 共振频率； 共振幅值

引 言

离心压缩机进出口管道振动破坏是压缩机组振动故障的主要表现形式之一，剧烈的管道振动会造成管道管壁、管道与机器的连接部件发生疲劳破坏、松动、破裂等故障。由于多数情况下管道内处理的是高压有毒气体，所以强烈的管道振动会影响压缩机组安全运行，甚至造成安全事故。因此，对于管道振动的研究有着不可回避的任务。

在压缩机组工作过程中，由于管道管壁的持续振动可能会造成支承件变形，使得其与管壁间产生间隙、松动，从而影响管道的动力学特性，因此有必要对更贴近实际工况的非线性支承的管道动力学特性进行研究。目前，大多数非线性约束的研究是基于管道梁模型[1-4]。但是，研究梁模型的运动仅限于管道的横向运动，适用于管长远远大于管径的厚壁管道振动分析，且其环向的模数较小。对于压缩机出口管道，其管长和管径之比往往较小，且多为薄壁管道，其振动现象更为复杂，壳模型才能够更准确地反映实际振动系统状况，揭示更多管道梁模型难以解释的现象。

对于薄壳模型，学者们也进行了许多研究。曹志远[5]系统地介绍了一系列的针对圆柱壳的分析方法。其他学者也对经典边界、弹性边界和特殊边界情况下各类圆柱壳振动做了许多工作，如刘彦琦[6]考虑不同边界条件下旋转薄壁圆柱壳的内力和固有特性。孙述鹏[7]引入弹簧对一般弹性边界下旋转圆柱壳进行建模，并利用正交多项式法对其固有特性进行了求解分析。A G Shah[8]基于波传播法对Pasternak基础下的多功能梯度圆柱壳进行了分析。Liu[9]分析了复杂激励下简支圆柱壳非线性动力学特性，分析激振力、几何缺陷和体分比对响应的影响。在流固耦合领域，张琪昌[10]基于Donnell简化壳理论，应用多尺度法研究了流体脉动激励下的薄壁圆柱壳非线性动力学特性。

虽然学者们在壳模型方面做了许多工作，但针对非线性支承下压力管道，尤其是对一端带有支承间隙的压力管道的研究尚不多见。本文引入管道圆柱壳模型，针对工程中管道管夹变形情况，建立了一端带有支承间隙的压缩机出口压力管道的简化模型。利用Ritz法对模型进行分析，通过数值计算得到管壁振动的幅频特性曲线。研究了支承刚度和支承间隙对管道动力学特性的影响。

1 带有支承间隙压力管道模型的建立

1.1 系统动力学简化模型

本文将一段压缩机出口压力管道列为研究对象，管道一端为焊接(固定支承)，另一端为管夹支承(间隙端)。根据所取管段的长径比较小，径厚比较大的结构特点，可建立压力管道的薄壁短圆柱壳简化模型，因此一端带有支承间隙的压力管道动力学简化模型如图1所示。根据薄壳理论，考虑中曲面上的点的运动来表示压力管道上各点的运动。在中曲面上任意位置处建立柱面坐标系o-xθz。其中x，θ，z分别代表管道的轴向、圆周方向(以下又称环向)和径向，相应三个方向的位移假设为u，v，w。同时管壁受到径向初始均匀分布的气流压力q。设其管道中曲面半径为R，管道厚度为h，长度为L，材料密度为ρ，弹性模量E，泊松比为μ。

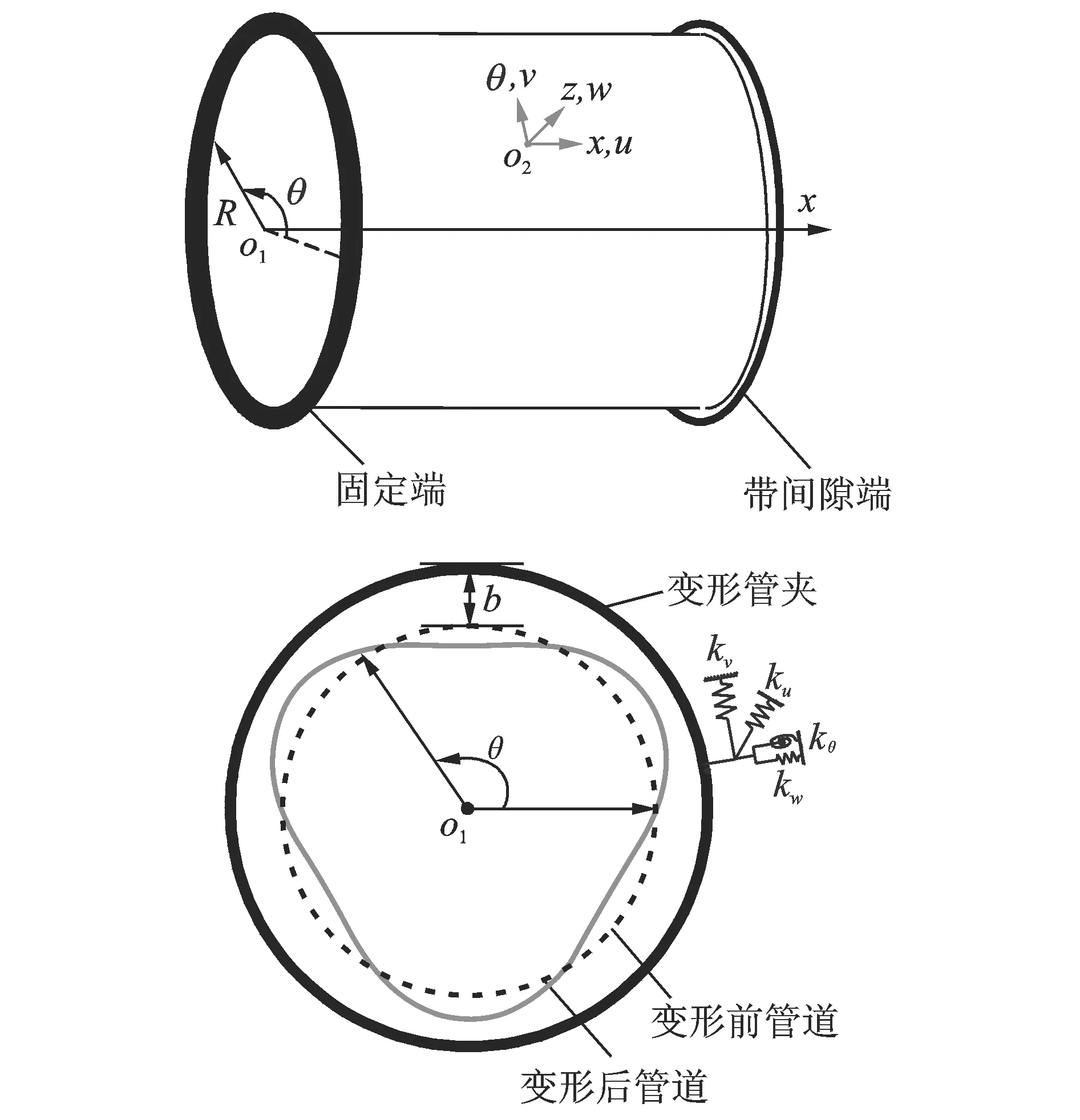
图1 一端带有支承间隙的压力管道动力学简化模型Fig.1 The simplified dynamic model of pipe segment with a clearance at one end

引入无质量弹簧组来描述管道管夹对管壁的约束作用，管夹与管道接触刚度也由弹簧刚度来近似表达，每组弹簧由4个弹簧组成，分别约束轴向、环向、径向和转向的变形，刚度值分别为ku，kv，kw和kθ。假设支承间隙为b；当管壁振动较小时，管夹与管道管壁相分离，此时的端部约束失效，弹簧等效刚度为0；当管壁振动较大时，管夹与管道管壁相接触，约束作用有效，等效线性刚度为k。故设带有支承间隙压力管道端等约束效刚度为：

ku,kθ=0，

(1)

1.2 压力管道振动微分方程

在柱面坐标系o-xθz中，管道中曲面上任意一点的振动速度为

(2)

则管道的动能可表示为

(3)

式中ξ为压力管道无量纲长度，ξ=x/L。

管道的应变势能表达式为

(4)

引入根据Sanders薄壳理论：

(5)

(6)

其中：

由于管道受到初始均匀分布的气流压力作用，从而引起管道受到周向应力[11]，则其引起管道变形的势能可表示为

(7)

综合应变势能和压力势能，则管道总势能为

U=Uq+Uε

(8)

由于管道内部气流压力不均匀度的影响，管道管壁受到径向冲击的脉动载荷的作用，因此可假设压力管道的管壁上某一点(x0，θ0)受到沿管道截面径向的集中气流激励，则可以表示为

fpz=Fpsin(ωt)

(9)

由1.1分析可知，在有间隙端的管夹对管道约束是分段线性的非线性力，其约束力可表示为

fsv=kvv|ξ=1;fsw=kw(w|ξ=1-b)

(10)

根据Ritz和Galerkin离散思想，管壁振动位移可以表示为：

u(ξ,θ,t)=UTa

(11a)

v(ξ,θ,t) =VTb

(11b)

w(ξ,θ,t) =WTc

(11c)

式中a，b和c为是与时间相关的广义坐标向量；U，V，W是满足边界条件约束的振型向量。

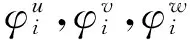
将式(11)代入式(3)，(8)和(9)得到动能、势能和气流激振力广义表达式：

(12)

(14)

其中，δ(x-x0)是狄拉克函数。

将式(11)代入(10)得到广义约束力表达式

(15)

因此管道的动能、应变势能和平均气流压力引起的势能，脉动气流激励以及边界弹簧约束力，再根据拉格朗日方程，得到压力管道振动非线性动力学微分方程

(16)

式中f(q)为广义弹簧力，为非线性力

f(q)=[0fsv(b)fsz(c)]T

阻尼矩阵C采用瑞利阻尼模型

C=αM+βK

(17)

其中，

式中ω1,ω2分别为第1，2阶固有频率，单位为Hz；ξ1,ξ2分别为对应的第1,2阶模态阻尼比。因此，带有支承间隙的压力管道模型是一个分段线性非线性振动微分方程。

2 带支承间隙压力管道的非线性特性及参数影响分析

2.1 带支承间隙压力管道的非线性特性

首先，假设在理想情况下，带管夹端的管道在工作过程中受线弹性支承，管壁振动响应幅频特性响应计算结果在图2中表示为“*”。可以看见，在气流脉动频率通过管道的固有频率时，振幅明显增大。对于有支承间隙端的支承刚度按式(1)来表示，在图2中以“o”表示基谐波幅频响应。结合图中曲线发现，由于支承间隙导致系统刚度成非线性，幅频曲线出现向右倾斜的硬化现象，共振峰较线弹性支承提前到来，且共振幅值增大。取共振峰值附近A，B，C，D四个区域进行比较，发现随气流脉动频率的增加，硬式非线性现象越来越明显。并且幅频特性曲线随着频率的连续变化过程中出现了明显的跳跃现象，如在脉动频率在750 Hz处发生明显的跳跃，这反映了在脉动频率变化过程中，在750 Hz处管壁响应点发生了比附近区域更大的相对运动，容易造成剧烈的冲击，从而产生很大的应力作用。

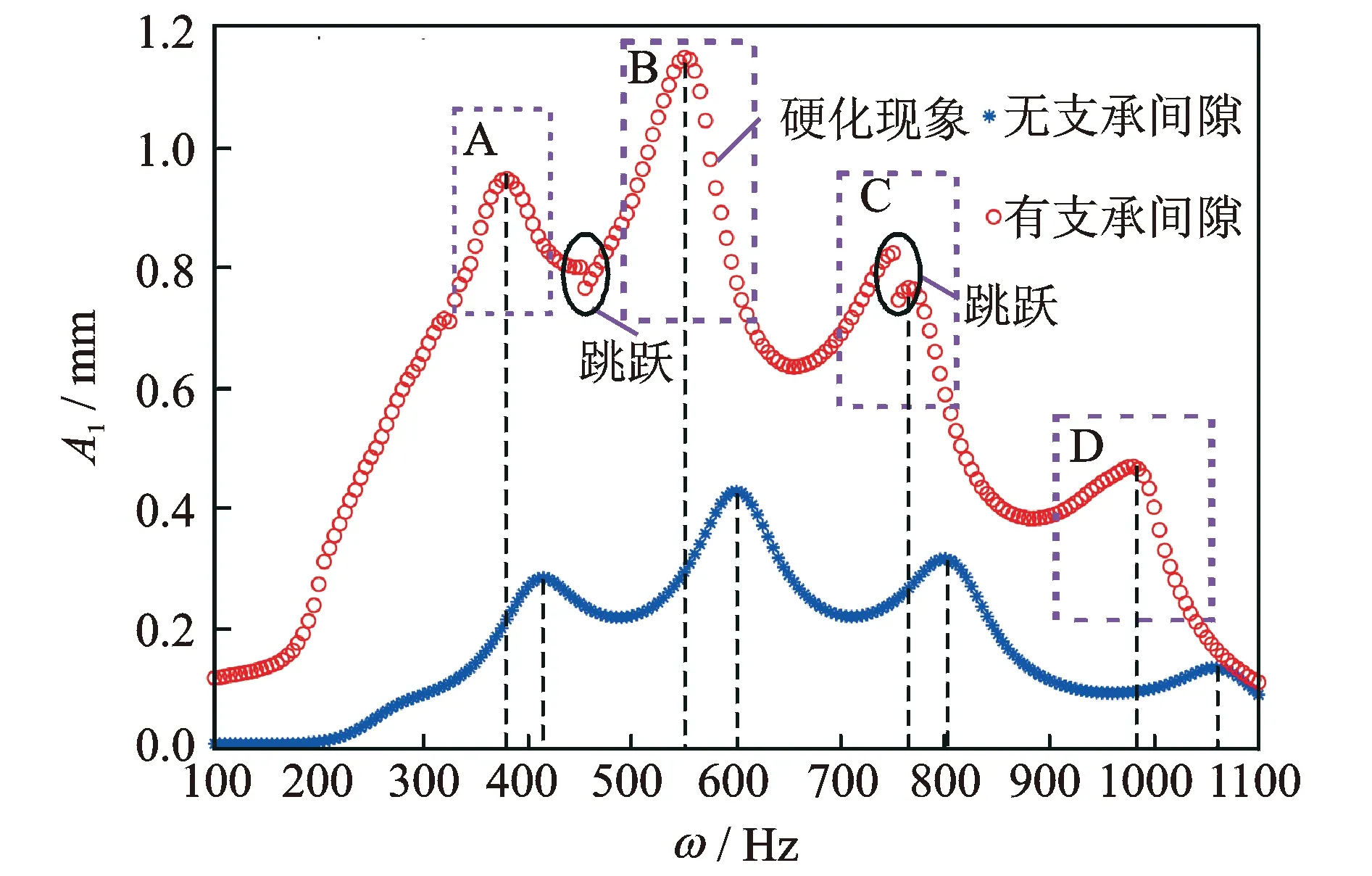
图2 基谐波频率-幅值响应曲线图Fig.2 A harmonic amplitude-frequency response curve

2.2 支承间隙的影响

从方程(16)可知，支承间隙是压力管道系统产生非线性现象的原因，不同的支承间隙值下管道系统也将呈现不同的振动特性，本节给出了b=0.2, 0.3和0.4 mm下各次谐波曲线图，如图3所示。其中，图3(a)是管壁振动响应的一次谐波幅频特性曲线。由图中可以看出，不同支承间隙下，系统都表现出明显的硬式非线性特性。可以发现，支承间隙对系统共振区和共振幅值有较大影响。支承间隙越大，系统等效刚度越小，共振区幅值越大，达到共振所要求的激振频率越小；同时，支承间隙越小，幅频曲线硬化现象越明显。由图3(b)可知，支承间隙对管壁振动响应的三次谐波幅频特性也有着重要的影响。在许多激振频率附近区域内三次谐波幅值较大，尤其在[600 Hz,800 Hz]区间内，幅值最大。因此在此类激振频率范围内，系统极有可能发生三阶频率共振。且在此范围内，系统幅频响应曲线软式非线性明显，并在最大幅值频率处发生跳跃现象。并且，间隙值越大，曲线峰值频率越小，幅值越大。图3(c)-(d)表示支承间隙对5次和7次振动谐波幅值的影响。可以发现，高次谐波主要集中出现在低频区间段，且间隙值对各次谐波幅值和频率影响不大。

2.3 支承刚度的影响

支承刚度是影响管道系统振动响应的又一个重要参数。图4表示的是间隙值b=0.3 mm时不同支承刚度下谐波随脉动频率的响应幅值变化图。从图4(a)可以看出，支承刚度对基谐波共振频率和共振振幅有较大影响。当k=5×108N/m时，在脉动频率为755 Hz处出现明显的跳跃现象，随着刚度值的减小，跳跃现象逐渐不明显。且随支承刚度减小，共振频率也减小，幅频曲线慢慢回正，硬式非线性现象逐渐减弱，但是响应幅值也随着逐渐增大。由图4(b)可知，支承刚度对管壁响应的3次谐波响应也有着较大的影响。在[400 Hz, 500 Hz] 区间内，支承刚度越大，跳跃现象愈加明显；在[600 Hz, 850 Hz]区间内支承刚度越大，曲线软式非线性现象越弱，并且刚度越大，共振幅值和共振频率也越大。由图4(c)-(d)可看出，支承刚度对5次和7次振动谐波幅值和共振频率也有着类似影响，但对比发现，随着谐波次数的增高，影响效果越来越不明显。

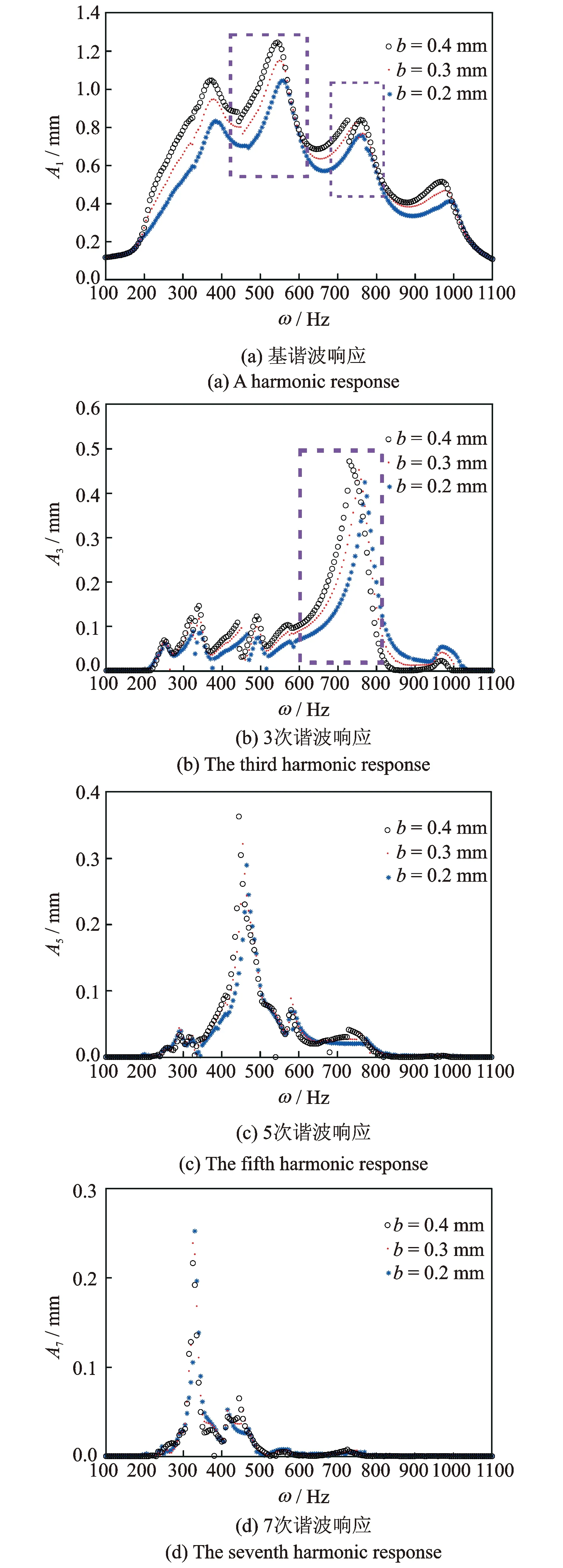
图3 不同支承间隙下各次谐波幅频特性曲线图Fig.3 Several harmonic amplitude-frequency response curves with different supported clearances

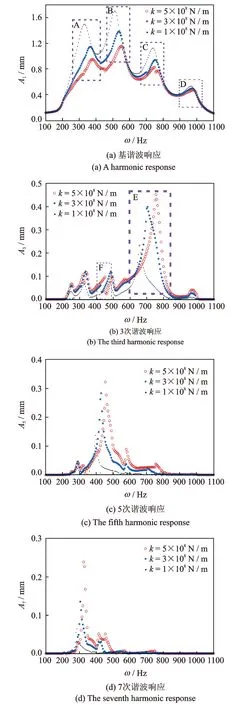
图4 不同支承刚度下各次谐波幅频特性曲线图Fig.4 Several harmonic amplitude-frequency response curves with different supported clearances

3 结 论

本文建立了一端带有支承间隙的压力管道的非线性动力学模型，研究了其在气流脉动载荷冲击下的非线性振动特性，通过管壁振动频幅响应特性分析了气流脉动频率、支承刚度和支承间隙对系统动力学特性的影响，研究结果如下：

(1)由于支承间隙的存在，导致压力管道振动幅频曲线呈非线性特征，并伴有明显的跳跃现象，容易在管壁上产生很大的冲击从而引起很大的应力作用，造成疲劳破坏，减小管壁寿命。管壁振动响应在一定的激振频率区间包含有3次、5次、7次等高阶谐波，且幅值很大，因此很可能引起高阶频率共振，进一步引起管道破坏。

(2)支承间隙是影响管道振动响应特性的一个重要参数。支承间隙越大，系统等效刚度越小，共振区幅值越大，达到共振所要求的激振频率越小。同时，支承间隙越小，基谐波幅频曲线硬化现象越明显。支承间隙对3次、5次和7次的共振幅值和共振频率也有着明显的影响。但对响应中更高阶谐波幅值的影响越来越小。

(3)支承刚度对共振频率和共振振幅有较大影响。当支承刚度减小时，基谐波硬式非线性现象逐渐减弱，高次谐波非线性现象逐渐增强。

[1] 任建亭,姜节胜.输流管道系统振动研究进展[J].力学进展,2003,33(3):313—332.

Ren Jianting, Jiang Jiesheng. Advances and trends on vibration of pipes conveying fluid[J]. Advances in Mechanics, 2003,33(3):313—332.

[2] 徐鉴,杨前彪.输液管模型及非线性动力学近期研究进展[J].力学进展,2004, 34(2):182—195.

Xu Jian, Yang Qianbiao. Recent development on models and nonlinear dynamcs of pipes conveying fluid[J]. Advances in Mechanics, 2004,34(2):182—195.

[3] 包日东,金志浩,闻邦椿.一般支承条件下输流管道的非线性动力学特性研究[J].振动与冲击,2009,28(7):153—157.

Bao Ridong, Jin Zhihao, Wen Bangchun. Nonlinear dynamic characteristics of a fluid conveying pipe under condition of commonly elastic supports[J]. Journal of Vibration and Shock, 2009,28(7):153—157.

[4] 包日东,金志浩,闻邦椿.分析一般支承输流管道的非线性动力学特性[J].振动与冲击,2008,27(7):87—90.

Bao Ridong, Jin Zhihao, Wen Bangchun. Analysis of nonlinear dynamic characteristics of commonly supported fluid conveying pipe[J]. Journal of Vibration and Shock, 2008,27(7):87—90.

[5] 曹志远.板壳振动理论[M].北京：中国铁道出版社，1989.

Cao Z Y. Vibration of Shells and Plates[M]. Beijing: China Railway Publishing House, 1989.

[6] 刘彦琦,秦朝烨,褚福磊.不同边界条件下旋转薄壁圆柱壳的振动特性[J].清华大学学报:自然科学版,2012,52(1):5—9.

Liu Yanqi, Qin Zhaoye, Chu Fulei. Vibration characteristics of rotating thin cylindrical shells for various boundary conditions[J]. Journal of Tsinghua University (Science and Technology), 2012,52(1):5—9.

[7] Sun S, Cao D, Han Q. Vibration studies of rotating cylindrical shells with arbitrary edges using characteristic orthogonal polynomials in the Rayleigh-Ritz method[J]. International Journal of Mechanical Sciences, 2013,68(3):180—189.

[8] Shah A G, Mahmood T, Naeem M N, et al. Vibrations of functionally graded cylindrical shells based on elastic foundations[J]. Acta Mechanica, 2010,211(3-4):293—307.

[9] Liu Y Z, Hao Y X, Zhang W, et al. Nonlinear dynamics of initially imperfect functionally graded circular cylindrical shell under complex loads[J]. Journal of Sound and Vibration, 2015,348:294—328.

[10]张琪昌,费杰,冯晶晶.薄壁圆柱壳在流体脉动激励下的振动特性分析[J].振动与冲击,2012,31(15):1—5.

Zhang Qichang, Fei Jie, Feng Jingjing. Vibration characteristic analysis of thin cylindrical shell excited by pulsating flow[J]. Journal of Vibration and Shock, 2012,31(15):1—5.

[11]Isvandzibaei M R, Jamaluddin H, Hamzah R I R. Frequency analysis of multiple layered cylindrical shells under lateral pressure with asymmetric boundary conditions[J]. Chinese Journal of Mechanical Engineering, 2014,27(1):23—31.

Nonlinear vibration of pressure pipe with support clearance at one end

TANGQian-sheng,LIChao-feng,WENBang-chun

(School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China)

Based on modern nonlinear dynamics and Sanders theory, nonlinear dynamic model of pressure pipe with support clearance was established and the Ritz method is used to analyze the model. And numerical method was applied to get amplitude frequency characteristic curve of the vibration of pipe wall. And the effect of supporting stiffness and support clearance on dynamic behaviors of pipe vibration were studied. Results show that the frequency-amplitude curves show the obvious nonlinear phenomenon. supporting stiffness and support clearance have a great impact on the resonant frequency and resonant amplitude of harmonic response, especially lower harmonic, of pipe vibration. To study on dynamic behavior of pressure pipe with supporting clearance is signification for daily work of designing, installing and maintenance.

nonlinear vibration; pressure pipe; clearance model; resonant frequency; resonant amplitude

2015-11-05；

2016-05-17

中央高校基本科研业务费专项资金资助项目(N140304002，N140301001)；辽宁省自然科学基金资助项目(2015020153)

O322

：A

1004-4523(2016)06-1028-06

10.16385/j.cnki.issn.1004-4523.2016.06.011

唐千升(1989—)，男，博士研究生。电话：18202436223； E-mail: qiansh-tang@163.com

李朝峰(1980—)，男，副教授。电话：13514215459； E-mail: chfli@mail.neu.edu.cn