偏心冲击下阻尼薄圆板动力学响应的广义多辛分析①

韩爱红， 胡伟鹏, 邓子辰

(1. 华北水利水电大学土木与交通学院，河南 郑州 450008；2. 西北工业大学力学与土木建筑学院，陕西 西安 710072；3. 大连理工大学工业装备结构分析国家重点实验室，辽宁 大连 116023)

偏心冲击下阻尼薄圆板动力学响应的广义多辛分析①

韩爱红1， 胡伟鹏2,3, 邓子辰2,3

(1. 华北水利水电大学土木与交通学院，河南 郑州 450008；2. 西北工业大学力学与土木建筑学院，陕西 西安 710072；3. 大连理工大学工业装备结构分析国家重点实验室，辽宁 大连 116023)

对称破缺是复杂动力学系统的本质属性，决定着系统诸多非线性性质。关注荷载不对称性和结构耗散这两类引起对称破缺的因素，采用广义多辛分析方法研究了偏心冲击荷载作用下阻尼薄圆板振动问题。在哈密顿体系下，建立偏心冲击荷载作用下阻尼薄圆板振动问题的动力学控制方程，构造其广义多辛近似对称形式，研究由于以上因素引起的守恒律误差。随后采用显式中点差分离散方法构造其广义多辛格式，并用于研究圆板阻尼和冲击荷载偏心对振动过程的影响。研究思路为进一步探索动力学系统的对称性与耗散效应之间的内在联系奠定基础。

薄圆板；偏心冲击荷载；哈密尔顿；广义多辛；对称性

引 言

1918年，德国女科学家Emmy Noether教授全面阐述了力学体系的连续对称变换与守恒量一一对应关系，即著名的诺特定理[1]。这一命题的创立一方面可以从力学系统的对称性研究过程中探索系统的守恒律[2]；另一方面，如果系统某种对称性被破坏，那么与之对应的守恒量也就不复存在。

在对粒子物理理论研究过程中，美籍科学家Yoichiro Nambu教授提出了对称破缺的概念，创立了著名的南部-戈德斯通定理[3]，由于这一创新性成果，Yoichiro Nambu教授同Makoto Kobayashi教授和Toshihide Maskawa教授一道分享了2008年诺贝尔物理学奖[4]。对称破缺是指物理学中，在具有某种对称性的物理系统之临界点附近发生的微小振荡，通过选择所有可能分岔中的一个分岔，打破了这物理系统的对称性，并且决定了这物理系统的命运。例如当水温降至接近冰点时，水中各处看起来皆相同，因此水系统具有空间上的对称性，此时若某处的温度振荡至低于冰点，便破坏了对称性，且决定了所凝固之冰的结构。动力学对称破缺是指描述动力学系统的Lagrange量或Hamilton量的某种对称性遭到破坏，Lagrange量或Hamilton量的破坏是耗散动力学系统耗散效应的内在动力，也是保结构算法需要保持的耗散动力学系统的本质属性。

薄板冲击动力学问题是飞机机身、装甲车车身等装备抗冲击设计中最基本的力学问题之一，在长期研究过程中，针对这一动力学问题，逐渐形成了两大类求解方法[5]：一类是吸收解析法结果准确和数值方法(主要是有限元法)处理边界灵活的优点而形成的半解析解法；另一类是在处理复杂的边界形状没有原则上的困难的数值方法。在已有工作中，已经采用保结构分析方法研究了薄圆板中心受冲击荷载作用下的振动问题[6]，本文将进一步考虑荷载偏心和结构阻尼对圆板振动的影响，采用保结构分析方法研究偏心冲击作用下阻尼薄圆板的振动问题[7]。

冯康先生在1984年双微国际会议上全面阐述了保结构算法的基本思想：数值分析过程与原连续系统应该在同一理论框架体系下进行，以此保证数值离散过程能够尽可能多地保持原连续系统的固有几何性质[8]，这一开创性的学术思想一直影响着保结构理论的发展：20世纪90年代，钟院士等针对Hamilton动力学系统建立了一套辛几何方法及时程精细积分理论[9]；Bridges教授等将针对有限维Hamilton系统的辛几何算法推广至针对无限维Hamilton系统的多辛算法，使得动力学系统局部性质的保结构分析成为可能，完善了保结构理论体系[10]；关注实际无限维动力学系统中广泛存在的耗散问题，邓子辰教授等将针对保守动力学系统的多辛算法推广至用于处理弱耗散动力学问题的广义多辛算法，进一步拓展了保结构思想的应用领域[11]。

基于本课题组前期研究工作，本文进一步考虑冲击荷载作用位置的偏心及其结构阻尼的影响，利用广义多辛算法研究偏心冲击荷载作用下中心对称阻尼薄圆板的动力学响应问题。

1 偏心冲击荷载作用下中心对称阻尼薄圆板振动模型及其近似对称形式

在已有工作基础上[6]，进一步考虑冲击荷载偏心和结构阻尼的影响，分析中心对称薄圆板动力学问题，如图1。假定圆板的几何尺寸是中心对称的，材料参数是均匀的，并且厚度可以忽略不计，则薄圆板振动问题可以简化为空间一维动力学问题，其振动控制方程可表述为

Aδ(0,τ) t≥0, 0≤r≤R, 0≤τ≤R

(1)

式中 ξ为圆板材料黏滞阻尼系数，ρ为薄圆板的面密度，D=Eh3/[12(1-ν2)]为薄圆板的抗弯刚度，E为圆板材料弹性模量，h为圆板厚度，ν为圆板材料泊松比，w=w(t,r)为挠度函数，R为圆板直径，Aδ(0,τ)为圆板受到的冲击荷载，A为冲击荷载的幅值，δ(0,τ)为冲击函数，表示在t=0时刻在r=τ的位置作用一个冲击荷载。

为了描述冲击荷载的偏心程度，定义相对偏心距

er=τ/R

(2)

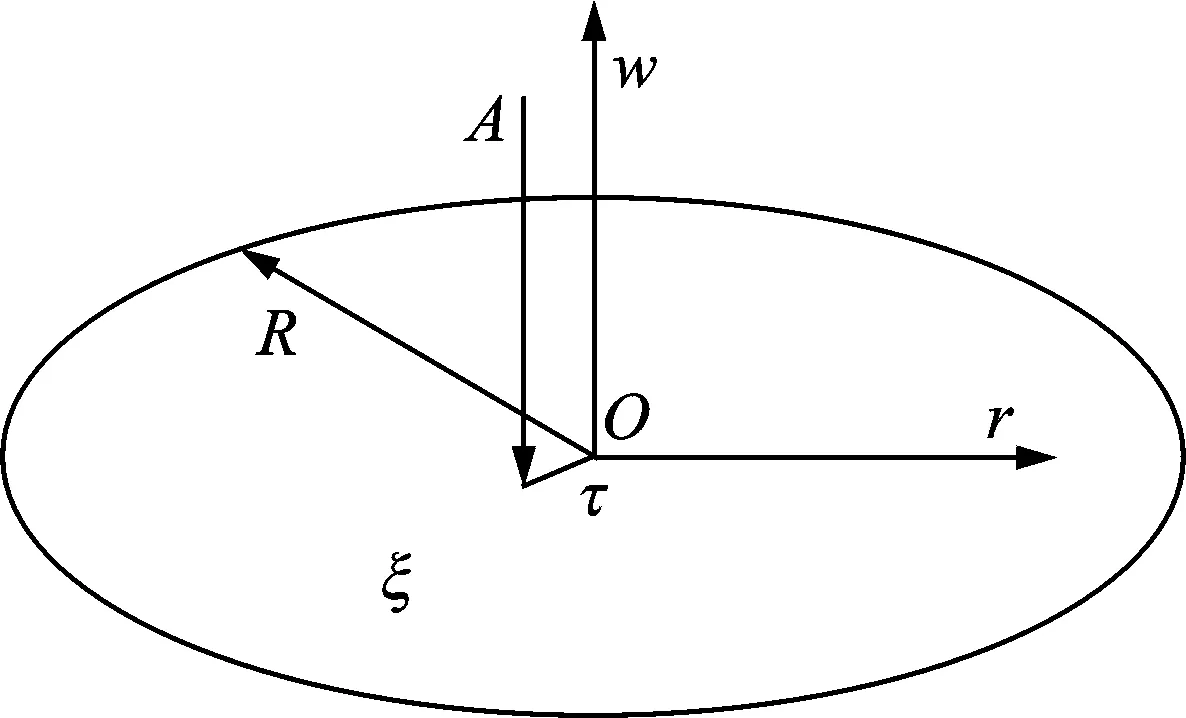
图1 计算模型Fig.1 Computational model

事实上，由于本文考虑的冲击荷载只是单个脉冲，该脉冲作用的时刻是初始时刻，因此冲击荷载的作用效果只反映在动力学问题的初值条件中，其偏心效应也只体现在数值求解方法的初值条件中，为此，本文首先考虑中心对称薄圆板的阻尼振动问题

t≥0, 0≤r≤R

(3)

薄圆板自由振动控制方程的多辛对称形式在文献[6]中已经给出，在此基础上，引入黏滞阻尼的影响，得到薄圆板阻尼振动的近似对称形式

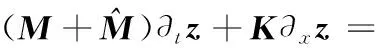
(4)

(1) 广义多辛守恒律

ρ∂t(du∧dw)+D∂r(dφ∧dw+dp∧dq)=

-ξd(∂tw)∧dw

(5)

式中 ∧为外积运算符，令右端项Δ=-ξd(∂tw)∧dw即是由于阻尼耗散引起的多辛守恒律误差。

(2) 近似局部能量守恒律

Dφ∂rw+Dq∂rp-Dp∂rq+Dw∂rφ)+

(6)

将Δel在时间区间[t1,t2]内对时间坐标做定积分，即得该局部在时间区间[t1,t2]内的能量耗散值；同理，将Δel在空间区间[r1,r2]内对空间坐标做定积分，也可以得该时刻在空间区间[r1,r2]内的能量耗散值。

2 广义多辛形式的多辛差分离散

出于计算效率考虑，本文采用显式中点差分离散方法构造广义多辛形式(4)的显式的广义多辛格式。

(7)

展开上式，即：

(8)

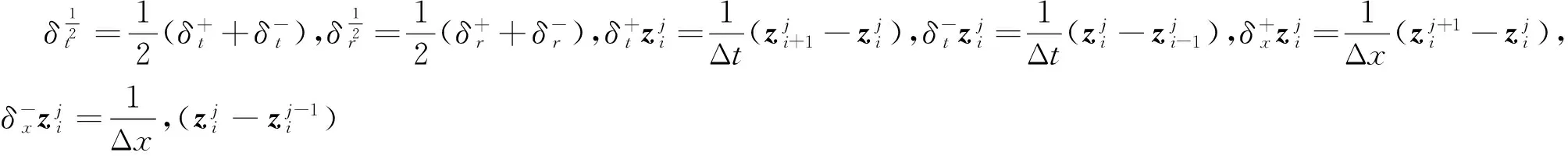
与广义多辛格式(8)相联系的是离散的广义多辛守恒律和离散的近似局部能量守恒律，即：

(9)

(10)

3 冲击荷载的偏心及材料的黏滞阻尼对薄圆板振动能量影响的数值研究

假定冲击荷载作用于r=τ这个圆周上的某一点，不失一般性，将该点所对应的极角设定为θ=θ0，θ0为一常数，在以下数值实验中，取θ0=π，这样，冲击荷载的初始条件可以列写为：

w(0,r)=0,∂tw(0,r)=0,

(11)

为简便起见，考虑固支撑边界条件

w(t,R)=0

(12)

选取薄圆板的几何尺寸参数：h=0.01 m，R=1 m，薄圆板材料参数为：ρ=78 kg/m2，E=200 GPa，ν=0.3。取计算步长为Δt=0.01 s，Δr=0.02 m。在t∈[0,5]s时段内，模拟不同相对偏心距和不同黏滞阻尼系数情形下，当冲击荷载幅值为A=1 kN时模拟薄圆板的振动情况，模拟不同相对偏心距和不同黏滞阻尼系数情形下圆板不同时刻的振动情况，结果如下(为了更好地表现荷载不对称，即初始条件不对称的影响，结果中只给出冲击荷载作用点所在的直径上的点的振动情况)：

3.1 荷载偏心的影响

为了研究冲击荷载偏心的影响，本部分假定黏滞阻尼系数为ξ=0.1，模拟当相对偏心距变化时薄圆板的振动情况，得到当相对偏心距为er=0.1和er=0.5时冲击荷载作用点所在直径上的点的振动情况如图2和3所示。

图2 圆板上θ=π直径上各点的挠度(er=0.1)Fig.2 Deflection of the grid point on the diameter in the θ=π direction with er=0.1

比较图2和3的模拟结果可知，在振动的初始阶段，随着冲击荷载偏心距的增大，圆板上冲击荷载作用点所在直径上的点的振幅减小，但是，随着振动的进行，偏心距越大，该直径上各点的振动随着偏心距的增大而加强。此外，随着偏心距的增大，振动波传播过程中的波长减小。

图3 圆板上θ=π直径上各点的挠度(er=0.5)Fig.3 Deflection of the grid point on the diameter in the θ=π direction with er=0.5

3.2 材料阻尼系数的影响

为了研究材料阻尼系数对圆板振动特性的影响，本部分假定相对偏心距为er=0.1，模拟取不同材料阻尼系数时薄圆板的振动情况，得到当阻尼系数为ξ=0.2和ξ=0.5时冲击荷载作用点所在直径上的点在t=5 s时的挠度分布情况如图4所示。

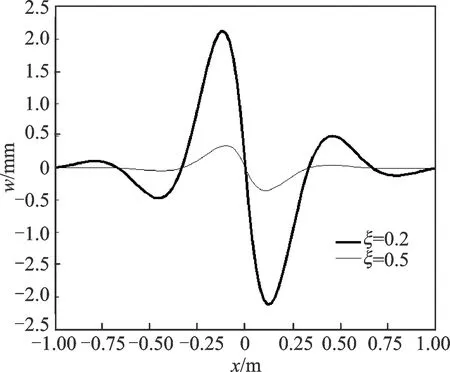
图4 圆板上θ=π直径上各点的挠度(ξ=0.2和ξ=0.5)Fig.4 Deflection of the grid point on the diameter in the θ=π direction with ξ=0.2 and ξ=0.5

比较不同阻尼系数下圆板振动情况，不难发现：随着圆板材料的阻尼系数增大，同一时刻圆板上各点的振动振幅减小，这正是能量耗散的结果。但是，振动波在圆板上传播的波长并不受圆板阻尼系数的影响。这说明在计算步长一定的情况下，随着圆板材料阻尼系数的增大，依据离散的多辛守恒律误差和离散的局部能量误差表达式，虽然多辛守恒律误差和局部能量误差有所增大，但是波在薄圆板中的传播特性依然得到了较好的保持。

4 结 论

本文考虑了两种影响动力学系统对称性因素，包括荷载的不对称性和阻尼耗散，其中，荷载不对称性由冲击荷载的偏心表现，这一因素在初始条件中体现；阻尼耗散效应由材料阻尼系数体现，采用广义多辛分析方法处理。详细研究了这两类因素对中心对称薄圆板振动特性的影响。通过对存在不同相对偏心距的冲击荷载作用下不同阻尼系数薄圆板振动特性的研究，发现：1) 随着偏心距的增大，圆板上各点的振动衰减减慢，同时振动波在圆板上传播的波长减小； 2) 随着材料阻尼系数的增大，薄圆板振动的振幅明显减小，而振动波的波长没有明显变化，即振动系统的几何特性得到了较好地保持。

[1] Noether A E. Invariante Variations-probleme, Nachr. Akad. Wiss. Göttingen[J]. Journal of Mathematical Physics, 1918, KI,II:235—257.

[2] Marsden J E, Ratiu T. Introduction to Mechanics and Symmetry[M]. New York: Springer-Verlag, 1999.

[3] Nambu Y. Axial vector current conservation in weak interactions[J]. Physical Review Letters, 1960, 4(7):380—382.

[4] Nambu Y. Nobel Lecture: spontaneous symmetry breaking in particle physics: A case of cross fertilization[J]. Reviews of Modern Physics, 2009, 81(3):1015—1018.

[5] Zhong W. Some developments of computational solid mechanics in china[J]. Computers & Structures, 1988, 30(4):783—788.

[6] 秦于越, 邓子辰, 胡伟鹏. 冲击荷载作用下中心对称薄圆板振动的多辛分析[J]. 西北工业大学学报, 2013, 31(6):931—934.

Qin Yuyue,Deng Zichen,Hu Weipeng. Multi-symplectic analysis of vibration of centrosymmetric thin circular plate under impact load[J]. Journal of Northwestern Polytechnical University, 2013, 31(6):931—934.

[7] 胡伟鹏, 邓子辰, 秦于越, 等. 偏心冲击下阻尼薄圆板动力学响应的广义多辛分析[C]. 中国计算力学大会2014暨第三届钱令希计算力学奖颁奖大会论文集, 成都,2014.

Hu Weipeng， Deng Zichen， Qin Yuyue，et al. Dynamic analyzing of thin damping circular plate under eccentric impact load by generalized multi-symplectic method[C] .CCCM2014, Chengdu, 2014.

[8] Feng K. On difference schemes and symplectic geometry[C]. Proceeding of the 1984 Beijing Symposium on D.D., Beijing: Science Press, 1984, 42—58.

[9] 钟万勰, 欧阳华江, 邓子辰. 计算结构力学与最优控制[M]. 大连: 大连理工大学出版社, 1993.

Zhong Wanxie ,Ouyang Huajiang, Deng Zichen. Computational Structural Mechanics and Optimal Control[M]. Dalian: Dalian University of Technology Press,1993.

[10]Bridges T J.Multi-Symplectic structures and wave propagation[J].Mathematical Proceedings of the Cambridge Philosophical Society, 1997, 121(1):147—190.

[11]Hu W, Deng Z, Han S, et al. Generalized Multi-symplectic integrators for a class of hamiltonian nonlinear wave pdes[J]. Journal of Computational Physics, 2013, 235:394—406.

Dynamic analyzing of thin damping circular plate under eccentric impact
load by generalized multi-symplectic method

HANAi-hong1,HUWei-peng2, 3,DENGZi-chen2, 3

(1.North China University of Water Resources and Electric Power, Zhengzhou 450008,China;2.Department of
Engineering Mechanics, Northwestern Polytechnic University, Xi′an 710072, China;3.State Key Laboratory of
Structural Analysis of Industrial Equipment, Dalian University of Technology, Dalian 116023, China)

Symmetry breaking is one of important properties of the complex dynamic system that affect the nonlinear characteristics of the dynamic systems. Focusing on the two typical symmetry case, including the asymmetry of the load as well as the dissipation effect, the vibration problem on the thin damping circular plate under the eccentric impact load is investigated by the generalized multi-symplectic method. Firstly, the control equation of the plate is established and the generalized multi-symplectic form is deduced for the control equation. And then, the errors of the conservation laws are given in the formwork of the generalized multi-symplectic theory. Finally, a generalized multi-symplectic scheme is constructed to simulate the vibration of the plate and the effects from the symmetry breaking are analyzed from the simulation results. The results obtained in this paper lay the foundation of the investigation on the relationship between the symmetry and the dissipation effect.

thin circular plate; eccentric impact load; Hamilton; generalized multi-symplectic; symmetry

2014-11-06；

2015-09-25

国家自然科学基金资助项目(11372252,11372253,11672241)；航空科学基金资助项目(2013ZB53020)；大连理工大学工业装备结构分析国家重点实验室开放基金资助项目(GZ1312)

TB122; O241.82

1004-4523(2016)06-0971-05

10.16385/j.cnki.issn.1004-4523.2016.06.004

韩爱红 (1982—),女,硕士，讲师。电话:15838045656;E-mail:hanaihong@ncwu.edu.cn