一维稳态流下非饱和土主动土压力强度计算模型

陈 茜， 郭光玲

(陕西理工大学 土木工程与建筑学院， 陕西 汉中723001)

一维稳态流下非饱和土主动土压力强度计算模型

陈 茜， 郭光玲

(陕西理工大学 土木工程与建筑学院， 陕西 汉中723001)

针对均质非饱和土层内含水率沿铅直方向变化的特点，基于总强度指标描述的朗肯主动土压力强度公式，结合非饱和土的重度、总强度指标与含水率之间的关系模型，得到了含水率铅直分布函数,推导出主动土压力系数、上覆土重和黏聚力的铅直分布函数，建立了非饱和土主动土压力强度计算模型。通过算例计算分析入渗、静水和蒸发等不同流动方向下，非饱和粉质黏土层内主动土压力系数和主动土压力强度的铅直分布规律。结果表明:不同流动方向下，主动土压力系数均随距地表深度增大呈现出非线性递减的规律，流动方向为入渗时主动土压力系数最小，静水条件次之，蒸发条件最大；主动土压力系数之间的差异随深度的增大而减小；主动土压力强度随距地表深度增大呈现出非线性递增的规律，流动方向对主动土压力强度的影响较小。

主动土压力强度； 主动土压力系数； 非饱和土； 含水率； 铅直分布

0 引 言

土压力计算是土力学研究中最重要、最基本的问题之一[1-2]。饱和土为固-液二相系统，饱和土的土压力计算仅需考虑土体重力和黏聚力的贡献[3-4]。对于非饱和土而言，其为固-液-气三相体系，物理力学性质复杂[5-7]。非饱和土层区别饱和土层的最显著特点是含水率沿铅直方向变化。该特点对土压力计算影响表现在非饱和土层内各点处土的重度、土压力系数和黏聚力不再是常数，而是沿铅直方向发生变化。因此，有效地获取非饱和土的重度、黏聚力和土压力系数与铅直方向深度之间的函数关系是解决非饱和土土压力计算的关键。

建立黏聚力及土压力系数与铅直方向深度之间关系模型的思路有二：其一是有效强度指标方法，该方法的主要特点是将有效应力原理引入非饱和土极限状态分析中，获取以有效内摩擦角为参量的土压力系数，进而获取包含有效黏聚力的土压力强度模型[8]；该方法建立的模型能够有效地揭示非饱和土的土压力强度构成要素和土压力的形成机制，在模型计算中将有效强度指标视为与含水率无关的常数，并需要测试该指标；另一种方法是总强度指标法，该方法的思路是非饱和土压力强度公式中涉及总强度指标和土重均可视为含水率的函数[9-11]，构建出非饱和土层内含水率沿铅直方向的分布函数，并将该函数分别代入总强度指标和土重与含水率之间的关系函数，获取总强度指标和土重的铅直分布函数，进而得到土压力系数和土压力强度表达式，与有效强度指标法相比，总强度指标法更容易为工程技术人员所接受。

鉴于此，笔者拟针对均质非饱和土层，基于总强度指标描述的朗肯主动土压力强度公式，以非饱和土的重度、总强度指标和与含水率之间的关系模型为桥梁，构建非饱和土主动土压力强度的计算模型，并通过算例计算分析不同流动方向下主动土压力系数和压力强度的铅直分布规律。

1 压力强度

经典朗肯主动土压力强度用总强度指标表示：

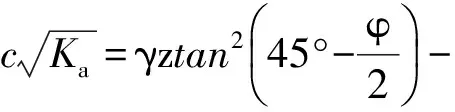
(1)

式中：pa——主动土压力强度；Ka——朗肯主动土压力系数；σ——任意深度z处上覆土重；γ——任意深度z处土的重度；z——土中一点距离地表的深度；c——黏聚力；φ——内摩擦角。

对于非饱和土层而言，土的重度γ、总强度指标c和φ均随质量含水率w的变化而变化，且含水率w与位置相关，可将土的重度γ、总强度指标c和φ以及主动土压力系数Ka和上覆土重σ等均视为相应深度z处含水率wz的函数，因此，当描述非饱和土主动土压力强度时，式(1)可写作：

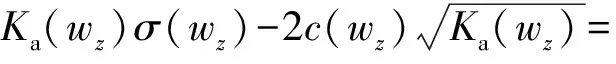
(2)

1.1 含水率的铅直分布

有效饱和度与质量含水率存在如下关系：

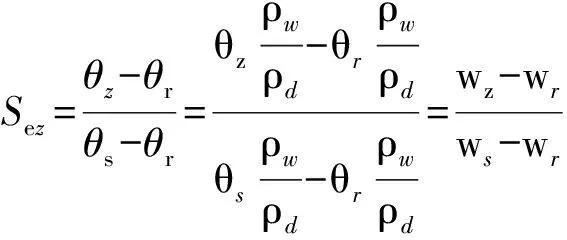
(3)

式中：Sez——距地表深度z处有效饱和度； θz——距地表深度z处体积含水率； θr——残余体积含水率； θs——饱和体积含水率； wr——残余质量含水率； ws——饱和质量含水率。

由式(3)可获得距地表深度z处质量含水率wz为

wz=Sez(ws-wr)+wr。

(4)

根据Van Genuchten模型[8]，有效饱和度Se与基质吸力(ua-uw)之间存在关系：

(5)

式中：α——渗透性函数中Gardner模型的拟合参数；

n——土水特征曲线拟合参数。

对于深度为H的非饱和土层，一维稳态流下在地下水位以上高度H-z处非饱和土基质吸力可表示为[8]

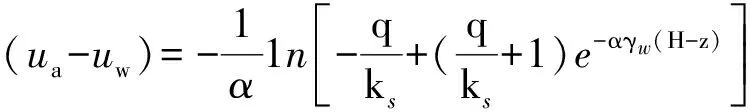
(6)

式中：q——比流量； ks——饱和渗透系数； γw——水的重度。

因此，由式(5)、(6)可得距地表z处(在地下水位以上高度H-z处)的有效饱和度：

(7)

将式(7)代入式(4)，则非饱和土中质量含水率w沿铅直方向的分布：

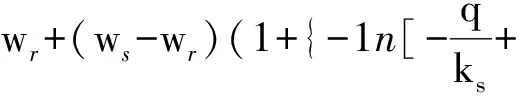
(8)

1.2 总强度指标和主动土压力系数的铅直分布

诸多学者对非饱和土的总强度指标与含水率的关系开展研究，其中内摩擦角与含水率关系模型的研究成果较为统一，即认为二者之间线性相关[11-16]。而黏聚力与含水率关系模型有线性模型[11-13]、分段线性模型[14]、多项式模型[15]和指数模型[16]等，其中线性模型应用最广。文中所采用的总强度指标与含水率关系模型为线性模型，如式(9)所示：

(9)

式中：a1、b1——黏聚力c的拟合系数；

a2、b2——内摩擦角φ的拟合系数。

将式(4)代入式(9)，则稳态流下总强度指标沿铅直方向分布可简洁地表示为

(10)

则，主动土压力系数Ka沿铅直方向的分布可简洁地表示为

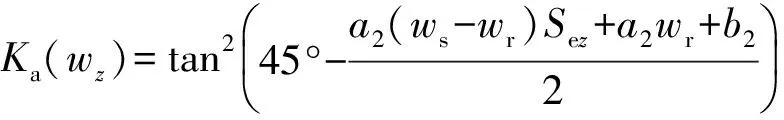
(11)

1.3 重度的铅直分布和主动土压力强度

均质半无限空间体的非饱和土层，其上覆土重的微分表达式为

dσ(w)=γ(wz)dz。

(12)

距地表任一深度处土的重度可用干重度γd表示为

γz=γd(1+wz)。

(13)

将式(8)代入式(13)，则非饱和土重度沿铅直方向的分布：

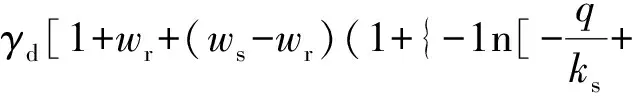
(14)

将式(14)代入式(12)并积分，非饱和土上覆土重沿铅直方向可简洁表示为

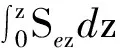
(15)

将式(10)和(15)代入式(2)，则主动土压力强度可简化为

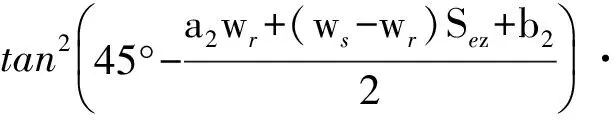
(16)

2 算例分析

2.1 计算参数

计算分析一维稳态流条件下流动方向分别为入渗、静水和蒸发时，主动土压力系数和主动土压力强度的铅直分布。设某粉质黏土地下水位以上土层厚度H为10 m，干重度γd为12.8 kN/m3，饱和质量含水率ws为41.6%，残余质量含水率wr为4.16%。黏聚力c的拟合系数a1、b1分别为-141.20和71.26 kPa，内摩擦角φ的拟合系数a2、b2分别为16.10°和16.72°，饱和渗透系数ks为2.5×10-7m/s，渗透性函数拟合参数α为0.008 kPa-1，土水特征曲线的拟合参数n为3，地表处的入渗率q在流动方向为入渗、静水和蒸发时分别为-3.14×10-8、0、1.15×10-8m/s。

2.2 主动土压力系数

将相关数据代入式(11)，计算不同流动方向下粉质黏土层内主动土压力系数铅直分布，结果如图1所示。由图1可见，不同流动方向下，均质非饱和粉质黏土层内主动土压力系数Ka随距地表深度z的增大呈现出非线性递减的规律，且递减的速率随距地表深度的增大而减小。造成这种现象的主要原因在于主动土压力系数Ka的大小与内摩擦角φ正相关，对于非饱和土而言，内摩擦角φ随含水率w的增大而减小，且学者们普遍认为二者之间线性相关。在均质非饱和土层内含水率w随距离地表的深度增加而增大(非饱和土至饱和土)，因此，主动土压力系数Ka和内摩擦角φ均随距离地表深度的增大而减小。

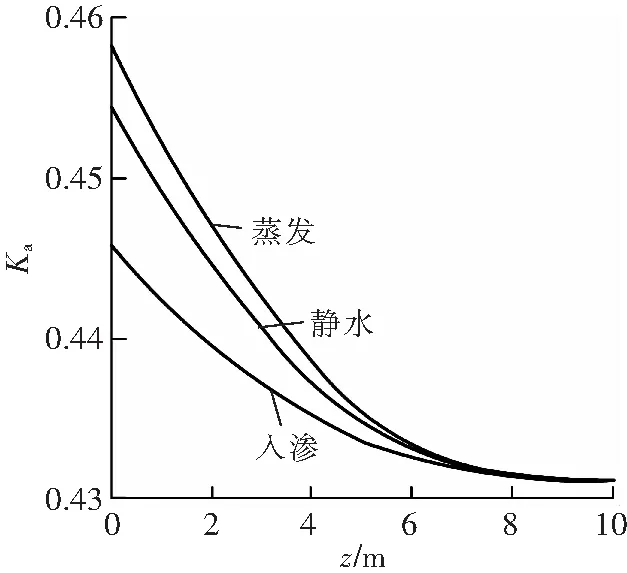
图1 不同流动方向下粉质黏土层内主动土压力系数

对比图1不同流动方向曲线可以发现，在距地表7 m处，入渗、静水和蒸发三种条件下，主动土压力系数Ka基本相同；在距地表0～7 m，Ka入渗时小于静水时，小于蒸发条件下Ka。上述分析表明，主动土压力系数Ka与含水率w负相关，而含水率w(或有效饱和度Se)沿深度z增大其变化速率在减小[8]，且越接近地下水位处不同流动方向下含水率w之间的差异越小，均趋近于同一个值——饱和含水率，因此，主动土压力系数Ka随距地表深度z增大呈现出减速递减的规律，越接近地下水位处不同流动方向下主动土压力系数Ka的差异越小。

2.3 主动土压力强度

将相关数据代入式(16)，计算不同流动方向下粉质黏土层内主动土压力强度，结果如图2所示。由图2可见，不同流动方向下均质非饱和粉质黏土层内主动土压力强度pa随距地表深度z的增大呈现出非线性递增的规律。其原因主要在于主动土压力强度pa的大小取决于主动土压力系数Ka、上覆土重σ和黏聚力c等参数。对于非饱和土而言，上述参数均受含水率w的影响，是深度z的非线性函数，分别如式(10)、(11)和(15)所示，因此，主动土压力强度pa与距地表深度z的增大呈现出非线性的关系。对比不同流动方向可见，主动土压力强度pa入渗时大于静水时，大于蒸发条件下pa，但差异较小，表明流动方向对主动土压力强度的影响较小。

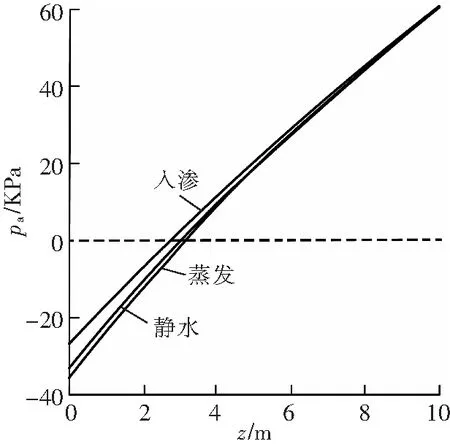
图2 不同流动方向下粉质黏土层内主动土压力强度

3 结 论

(1)含水率可表示为有效饱和度的函数, 结合描述有效饱和度和基质吸力关系的Van Genuchten模型及一维稳态流下非饱和土基质吸力铅直分布的解析解，获得了含水率铅直分布函数。

(2)非饱和土的内摩擦角与含水率的关系可用线性模型描述，结合含水率铅直分布函数，得到非饱和土层内内摩擦角的铅直分布函数，将其代入主动土压力系数表达式，得到主动土压力系数的铅直分布函数。

(3)非饱和土的黏聚力与含水率的关系可用线性模型描述，基于含水率铅直分布函数，得到非饱和土黏聚力的铅直分布函数；将主动土压力系数、上覆土重和黏结力的铅直分布函数引入总强度指标描述的朗肯主动土压力强度公式，获得非饱和土主动土压力强度与距离地表深度之间的函数关系。

(4)对一维稳态流下不同流动方向的非饱和粉质黏土层内主动土压力系数和主动土压力强度进行计算和分析。随地表深度增大，主动土压力系数呈非线性递减趋势，流动方向对主动土压力系数影响表现为，入渗时主动土压力系数最小，静水时居中，蒸发时最大，但这种差异随深度的增大而减小；随地表深度的增大，主动土压力强度呈非线性递增趋势，流动方向对其影响较小。

[1] 杨 剑. 复杂条件下黏性土主动土压力解析解[J]. 河海大学学报: 自然科学版, 2012, 40(4): 380-386.

[2] 张常光, 张庆贺, 赵均海. 非饱和土抗剪强度及土压力统一解[J]. 岩土力学, 2010, 31(6): 1871-1876.

[3] 汪丁建, 童龙云, 邱岳峰. 降雨入渗条件下非饱和土朗肯土压力分析[J]. 岩土力学, 2013, 34(11): 3192-3136.

[4] 李顺群, 高凌霞, 柴寿喜, 等. 饱和非饱和土的位移土压力及非极限力学指标研究[J]. 中国公路学报, 2013, 26(2): 26-33. [5] WEI C F, DEWOOLKAR M M. Formulation of capillary hysteresis with internal state variables[J]. Water Resources Research, 2006, 42(7): 425-430.

[6] FLYNN D, MCNAMARA H, O’KANE P, et al. Application of the Preisach model in soil-moisture hysteresis[M]. New York: Elsevier, 2006.

[7] LI X S. Modeling of hysteresis response for arbitrary wetting/drying paths[J]. Computers and Geotechnics, 2004, 32(2): 133-137. [8] LU N, WILLIAM J L. 非饱和土力学[M]. 北京: 高等教育出版社, 2012: 178-190.

[9] FREDLUND D G, RAHARDJO H. 非饱和土土力学[M]. 陈仲颐, 张在明, 陈愈炯, 等译. 北京: 中国建筑工业出版社, 1997.

[10] 李广信. 高等土力学[M]. 北京: 清华大学出版社, 2004.

[11] 凌 华, 殷宗泽. 非饱和土强度随含水量的变化[J]. 岩石力学与工程学报, 2007, 26(7): 1499-1503.

[12] 申春妮, 方祥位, 王和文, 等. 吸力、含水率和干密度对重塑非饱和土抗剪强度影响研究[J]. 岩土力学, 2009, 30(5): 1347-1351.

[13] 高 帅, 骆亚生, 胡海军, 等. 非饱和原状黄土增湿条件下力学特性试验研究[J]. 岩土工程学报, 2015, 37(7): 1-5.

[14] 王海东, 高昌德, 刘方成. 含水率对非饱和砂土力学特性影响的试验研究[J]. 湖南大学学报： 自然科学版, 2015, 42(1): 90-96.

[15] 边加敏, 王保田. 含水量对非饱和土抗剪强度参数的影响研究[J]. 地下空间与工程学报, 2011, 7(1): 19-25.

[16] 胡 昕, 洪宝宁, 王海明, 等.高液限土和煤系土抗剪强度的水敏感性比较研究[J]. 四川大学学报: 工程科学版, 2010, 42(1): 54-59.

(编校 王 冬)

Active earth pressure strength model of unsaturated soil

ChenXi,GuoGuangling

(School of Civil Engineering & Architecture, Shaanxi Sci-Tech University, Hanzhong 723001, China)

This paper highlights a novel calculation model for the active earth pressure strength in unsaturated soil， which responds to the way the water content in homogeneous unsaturated soil varies along vertical direction. The model is developed by identifying the water content vertical distribution function and the coefficient of active earth pressure and deducing overlying soil heavy and cohesion vertical distribution function, using the Rankine active earth pressure strength formula, coupled with the relationship model between soil gravity density, water content and total shear strength parameters in unsaturated soil layer. The paper is focused on the calculation and analysis of the law underlying the vertical distribution of active earth pressure strength, together with active earth pressure coefficient in unsaturated silty clay layer, when flow directions vary from infiltration to static water to evaporation. The results demonstrate that active earth pressure coefficient behaving in different flow direction exhibits a nonlinear decrease with an increasing depth; the minimum coefficient occurs in the active earth pressure when the flow direction is infiltration, followed by hydrostatic condition and the evaporation condition is maximum; the decreasing differences in active earth pressure coefficient depends on the increasing depth; the active earth pressure strength is governed by a nonlinear increase due to an increasing depth, and the flow direction exerts a smaller effect on active earth pressure strength.

active earth pressure strength; coefficient of active earth pressure; unsaturated soil; water content; vertical distribution

2016-10-01

中央高校基本科研业务费专项资金项目(310829151076)

陈 茜(1984-),女,陕西省泾阳人,讲师,博士,研究方向:非饱和土理论,E-mail:616137105@qq.com。

10.3969/j.issn.2095-7262.2016.06.023

TU432

2095-7262(2016)06-0700-05

:A