横向联接破坏对T梁桥荷载横向分布的影响

李 科， 李 涛， 杜伟强

(东北石油大学 土木建筑工程学院， 黑龙江 大庆 163318)

横向联接破坏对T梁桥荷载横向分布的影响

李 科， 李 涛， 杜伟强

(东北石油大学 土木建筑工程学院， 黑龙江 大庆 163318)

为了研究横向联接破坏对T梁桥荷载横向分布的影响，根据破坏位置和破坏形式的不同,划分九种工况建立有限元模型，通过计算得出每种工况下各主梁的荷载横向分布数值,并与无损伤情况下数值进行对比分析。结果表明：横向联接破坏会引起荷载横向重分布，各主梁的荷载横向分布数值均发生变化，且随着破坏程度加重变化幅度也愈加明显；受荷载直接作用的主梁荷载横向分布数值在横向联接破坏后大幅度增加变为最大值；横向联接破坏后以破坏点为界线，荷载作用一侧的主梁荷载横向分布数值增大而另一侧则减小。该研究得到了横向联接破坏下桥梁荷载横向分布的变化规律，可为实际工程施工和T梁桥的加固维修提供理论参考。

横向联接； T梁桥； 荷载横向分布； 有限元

装配式简支T梁桥因受力明确、构造简单、预制安装方便等诸多优点在高速公路、一般公路和城市桥梁中得到广泛应用[1]。此类桥梁主要由承重结构(主梁)及传力结构(横隔梁和桥面板)两部分组成，各主梁间依靠横隔梁或桥面板等横向联系构件联接成空间整体结构，当桥上作用荷载时，各片主梁将共同参与工作分担荷载，形成了各片主梁之间的荷载横向分布。这种分布规律与结构横向联接刚度有着密切的关系，横向联接刚度越大荷载横向分布作用越显著，各主梁负担的荷载也越趋均匀[2]。这类桥梁在投入使用后普遍出现横向联接薄弱或退化等现象[3-6]，致使结构横向联接刚度变低，从而改变了桥梁原有的荷载横向分布规律。

现阶段针对梁桥荷载横向分布的研究主要侧重于无损伤桥梁的荷载横向分布计算，对于有损伤桥梁的荷载横向分布计算研究较少[7]，有关横向联接破坏对桥梁荷载横向分布影响的研究更是少见。然而，现役桥梁都不同程度地存在着一定的横向联接破坏，桥梁荷载横向分布均匀性降低，致使其承载力与设计初始值有所不同，直接影响桥梁的正常使用和使用寿命。因此，有必要对桥梁横向联接破坏后其荷载的横向分布变化进行研究。笔者根据破坏位置和破坏形式的不同划分九种工况建立有限元模型，借助ANSYS软件进行分析，得出各种工况下T梁桥荷载横向分布数值，并与无损伤情况下的数值进行对比，进而探讨不同工况下T梁桥荷载横向分布数值的具体变化规律。

1 无损伤模型建立与验证

1.1 有限元模型建立

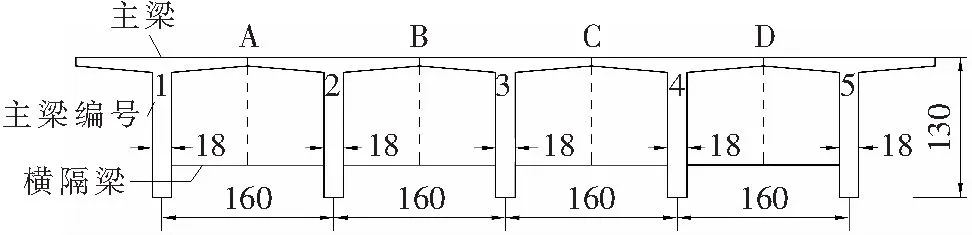
a 横向尺寸

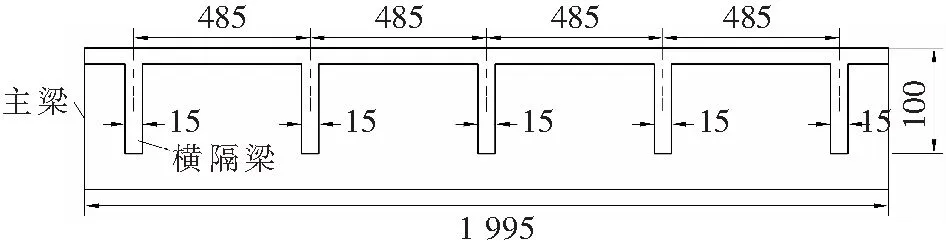
b 纵向尺寸

利用ANSYS14.0建立有限模型如图2所示，模型边界为各主梁前端面底部节点施加x、y方向自由度约束，后端面底部节点施加x、y、z方向自由度约束，模型左右两侧自由。

图2 有限元计算模型

1.2 模型准确性验证

G-M法(比拟正交异性板法)因理论成熟、概念明确、计算结果接近实际等诸多特点，在工程当中得到了广泛应用，故文献[8]利用G-M法计算得出了上述桥梁的荷载横向分布数值(表1)，具体计算过程可参阅文献[8]，文中不作详细介绍。考虑到利用G-M法计算简支T梁桥荷载横向分布数值，可以比较精确地反映实际结构的荷载横向分布情况。文中将有限元模型计算出的数值与文献[8]的数值进行对比，通过考察两组数值的吻合程度来验证所建模型的正确性，数据对比情况如表1所示。

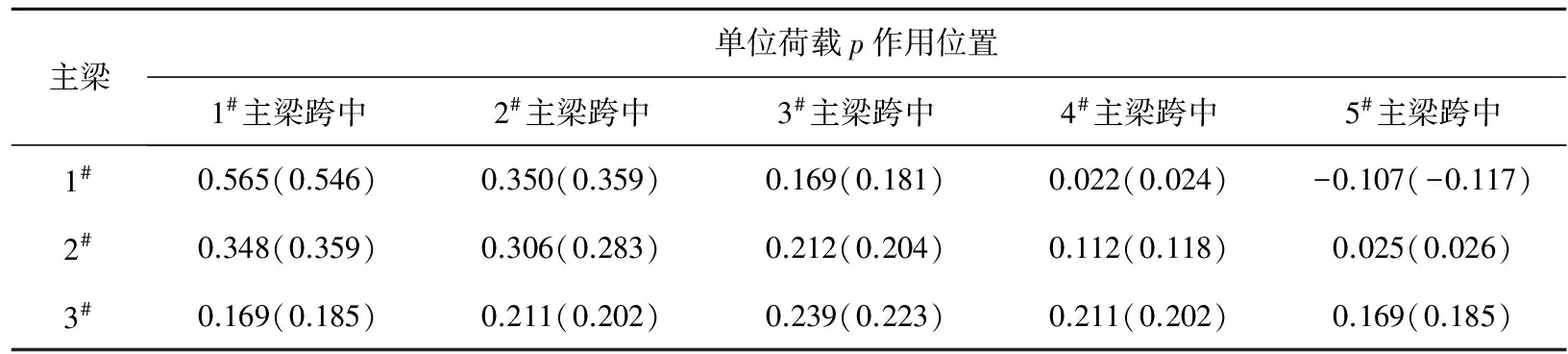
表1 荷载横向分布数值

注：括号内为文献[8]的数据。

分析表1中数据可知，文中模型计算出的数值和文献[8]的十分接近，最大误差仅为-9.50%。误差是由于文献[8]利用G-M法计算荷载横向分布数值过程中采用了表格插值和近似计算。上述数值对比说明文中所建模型精度满足工程需求，可以作为计算荷载横向分布数值的模型。

2 模拟结果与分析

装配式简支T梁桥主梁之间的横向联系主要通过T梁翼缘之间的联接和横隔梁之间的联接来实现，而这些联接部位在桥梁建设时一般要在桥梁主体结构完工后再进行施工，因此，这些部位相对薄弱。在桥梁使用过程中，这些部位也相对容易发生破坏，而且往往不容易在其破坏初期被发现，但是其破坏经常会危及整座桥梁的使用安全，所以文中按照破坏发生的位置(Ⅰ类，图1中A处破坏；Ⅱ类，B处破坏；Ⅲ类，AC处破坏)，结合纵缝(T梁翼缘联接处)单独破坏、横隔梁联接单独破坏以及二者共同破坏三种破坏形式，分析了横向联接破坏对荷载横向分布的影响。

在前文无损伤模型基础上调整节点耦合方式模拟桥梁横向联系破坏建立损伤模型，通过有限元软件计算得出各工况下桥梁荷载横向分布数值。为了能直观地反映数据变化，以受荷载直接作用的主梁编号为横坐标，以荷载横向分布数值为纵坐标，将各工况下桥梁荷载横向分布数值与无损伤情况下的数值进行对比，并绘制对比曲线如图3～5所示。

2.1 边梁荷载横向分布

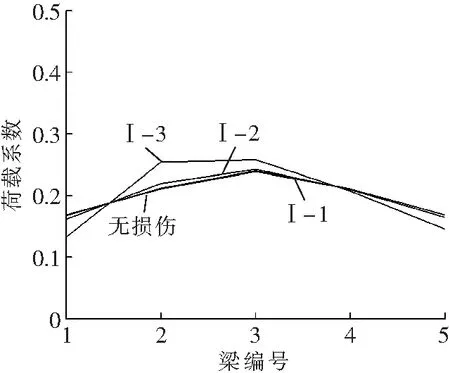
由图3可见，T梁桥横向联接受到破坏后，1#梁(左边梁)荷载横向分布数值有明显变化。图3a、b、c中工况Ⅰ-1、Ⅱ-1、Ⅲ-1的曲线都与无损伤曲线基本保持重合，可知当纵缝联接单独破坏时，1#梁的荷载横向分布数值基本保持不变；由图3a、b、c中工况Ⅰ-2、Ⅱ-2、Ⅲ-2的曲线可以看出，与纵缝联接单独破坏相比，横隔梁联接单独破坏，对1#梁的荷载横向分布数值影响较大；当单位荷载作用在两侧边梁(1#梁和5#梁)时，1#梁荷载横向分布数值增大，其中荷载作用在1#梁本身时这一变化尤为明显；当单位荷载作用在其余各梁时，1#梁荷载横向分布数值减小；观察图3a、b、c中曲线的变化情况发现，T梁桥横向联接破坏位置一定时，1#梁荷载横向分布数值的变化幅度与桥梁横向联系的破坏程度有关，破坏程度越重变化幅度就越大；如果在横隔梁联接破坏的基础上纵缝联接再发生破坏，那么1#梁的荷载横向分布数值的变化幅度就会达到最值。为了便于观察分析，将图3a、b、c中工况Ⅰ-3、Ⅱ-3、Ⅲ-3的曲线与无损伤曲线进行对比，如图3 d所示。观察图3 d可以发现，相同的破坏形式(破坏程度一致)发生在图1中B位置时，对1#梁的荷载横向分布数值的影响要大于发生在A位置时，AC两处都发生破坏时1#梁的荷载横向分布数值受到的影响最大。

a Ⅰ类工况

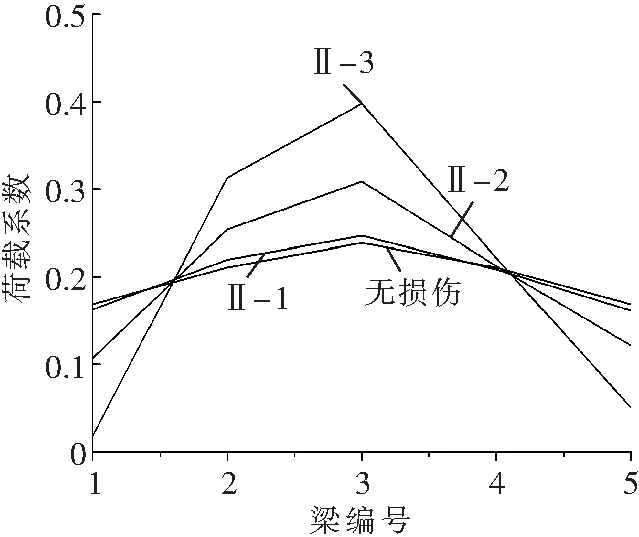
b Ⅱ类工况

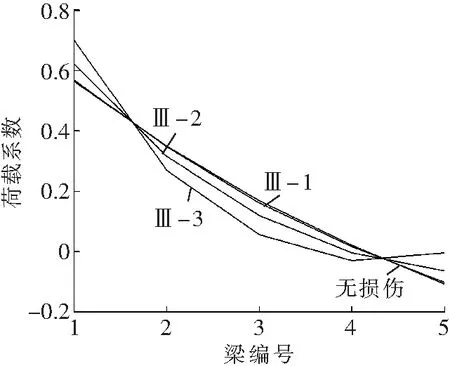
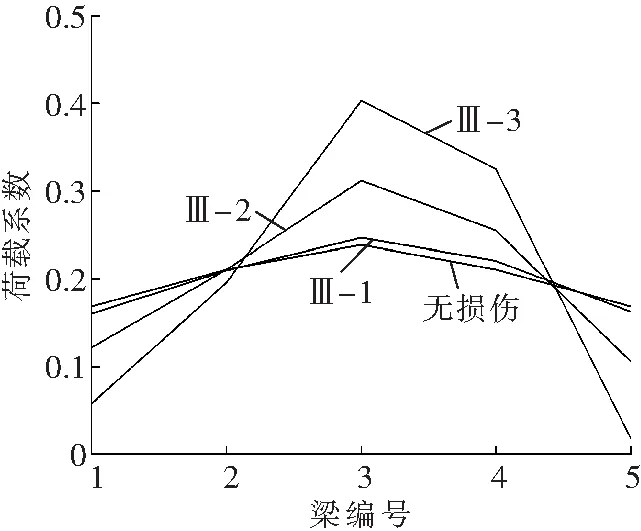
c Ⅲ类工况

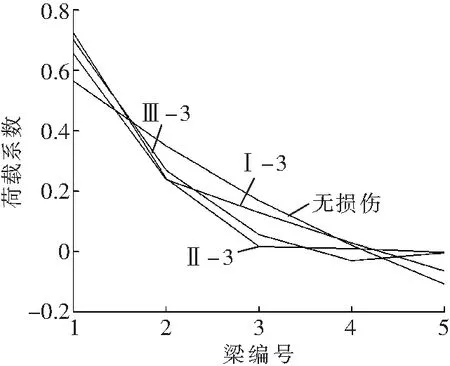
d 多类工况

2.2 次边梁荷载横向分布

观察图4可以发现，T梁桥横向联接破坏对2#梁(左次边梁)荷载横向分布数值的影响同1#梁一致，当T梁桥横向联接破坏位置一定时，2#梁荷载横向分布数值的变化幅度随着桥梁横向联系破坏程度的加重而变大，当纵缝联接与横隔梁联接共同破坏时达到最值。将图4a、b、c中各工况的曲线与无损伤曲线进行比较发现，与1#梁荷载横向分布数值变化相反，当单位荷载作用在两侧边梁时，2#梁荷载横向分布数值明显减小；当单位荷载作用在2#梁本身和其余梁时，2#梁荷载横向分布数值增大；2#梁更为明显的变化是在横隔梁联接处没有产生破坏时，2#梁荷载横向分布数值的最大值出现在单位荷载作用于1#梁时，而在横隔梁联接处破坏以后，2#梁荷载横向分布数值的最大值却出现在单位荷载作用于其本身时，并且数值较前者明显增大；将图4a、b、c中工况Ⅰ-3、Ⅱ-3、Ⅲ-3的曲线与无损伤曲线进行对比，如图4d所示。观察图4d可以发现，同1#梁不同的是，相同的破坏形式发生在图1中B位置时，2#梁的荷载横向分布数值变化幅度相比发生在A位置时要小。同1#梁一致的是,当AC两处都发生破坏时，2#梁的荷载横向分布数值变化幅度同样是最大的。

2.3 中间梁荷载横向分布

由图5可见，与前两道梁一致，破坏位置一定时，3#梁(中间梁)荷载横向分布数值的变化幅度随着横向联接破坏程度的加重而变大，当纵缝联接与横隔梁联接共同破坏时达到最值。观察图5a、b、c中各工况曲线可以发现，横向联接破坏后当单位荷载作用在两侧边梁时，3#梁荷载横向分布数值减小；当单位荷载作用在其他梁时，3#梁荷载横向分布数值增加，其中单位荷载作用在3#梁本身时其荷载横向分布数值增加幅度最大；观察图5d可以看出，当横向联接破坏发生在图1中A位置时，3#梁荷载横向分布数值受到的影响较小，即使横向联接破坏程度加重，该梁的荷载横向分布数值也没有明显变化；当横向联接破坏发生在图1中B位置时，3#梁荷载横向分布数值受到影响较大，且随着破坏程度的加重影响也随之加大。

a Ⅰ类工况

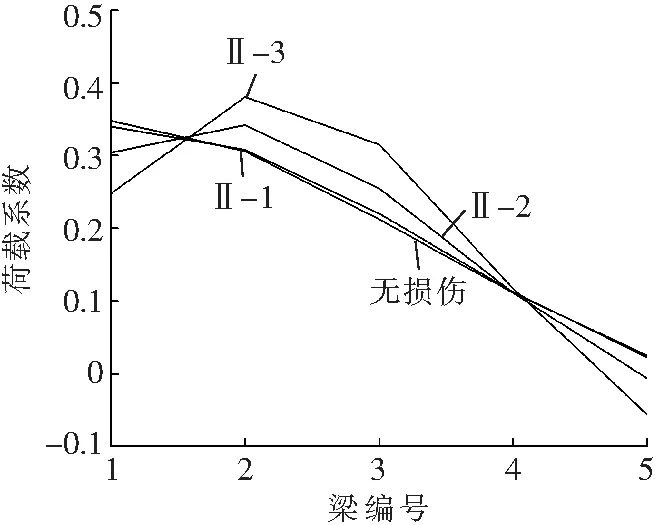
b Ⅱ类工况

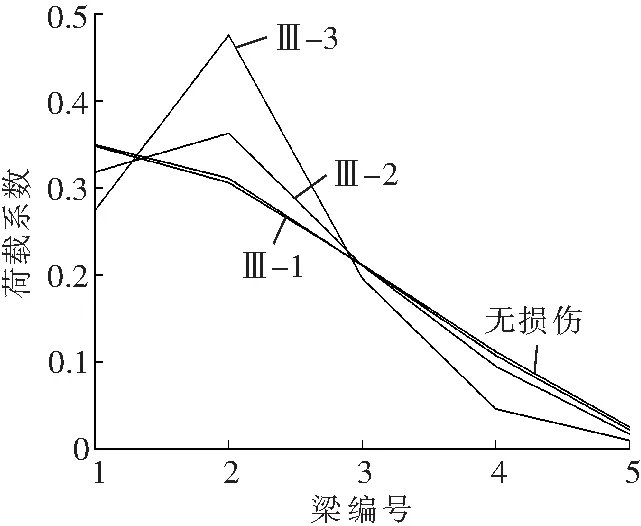
c Ⅲ类工况

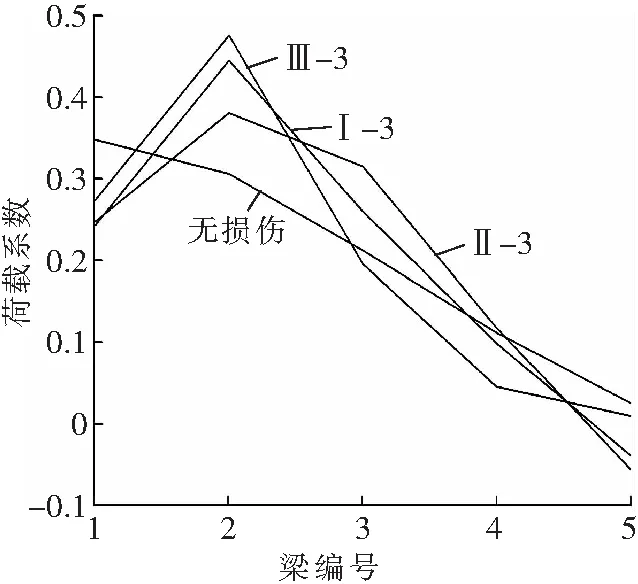
d 多类工况

a Ⅰ类工况

b Ⅱ类工况

c Ⅲ类工况

d 多类工况

3 结 论

(1)横隔梁联接完好时纵缝联接破坏对T梁桥荷载横向分布影响较小，即使破坏的纵缝数量增加其影响也没有明显提高。

(2)横隔梁之间的联接对T梁桥荷载横向分布起到重要作用，如果横隔梁联接处发生破坏将会引起荷载横向重分布。纵缝之间的联接对T梁桥荷载横向分布的影响虽不像横隔梁那样突出，但也不可忽视。如果横隔梁联接已经破坏，那么纵缝之间的联接对荷载横向分布将起到主要作用，此时纵缝之间的联接若也发生破坏，那么将会引起荷载横向再次重分布。

(3)T梁桥横向联接破坏达到一定程度时，破坏位置和破坏数量对荷载横向分布均有影响，且随着破坏程度加重影响也愈加明显。具体表现为：横向联接破坏后，受荷载直接作用的主梁其荷载横向分布数值显著增加变为最大值；如果破坏位置靠近这道主梁或破坏数量增加，那么这道主梁的荷载横向分布数值会在原有基础上有所增大。

(4)横向联接破坏后，以破坏点为界线两侧主梁的荷载横向分布数值变化趋势截然相反，荷载作用一侧的主梁荷载横向分布数值随着破坏程度的增加而增大，另一侧则减小。这表明横向联接破坏时，破坏点处横向传递力的能力有所下降，并且随着横向联接破坏程度的加重这一能力下降的就愈加明显。

[1] 陈科健. 装配式T形梁桥横向联结的限元分析及加固研究[D]. 长沙: 中南大学, 2011: 1-36.

[2] 李秀芳, 吴锐福. 无伸缩缝桥梁荷载横向分布系数的有限元分析[J]. 公路交通科技, 2013, 30(12): 86-92.

[3] 姚晓飞, 徐 岳. 公路混凝土T梁桥结构体系损伤评定[J]. 广西大学学报:自然科学版, 2010, 35(1): 120-126.

[4] 陈勇军, 张会远. 桥梁横向分布系数计算方法对比分析研究[J]. 公路工程, 2015, 40(3): 148-151.

[5] 张立东, 孙全胜. 空心板梁桥铰缝损坏对横向分布的影响[J]. 山西建筑, 2015, 41(23): 144-146

[6] 李 波, 武 建. 在役装配式简支T梁桥加固前后横向分布系数试验研究[J]. 中外公路, 2015, 35(5): 167-170.

[7] 魏保立, 邓苗毅. 损伤桥梁的荷载横向分布计算方法研究[J]. 河南理工大学学报: 自然科学版, 2015, 34(1): 102-108.

[8] 姚森玲. 桥梁工程[M]. 北京: 人民交通出版社, 2008: 143-156.

(编校 王 冬)

Influence of transverse load distribution of T beam bridge under transverse connection damages

LiKe，LiTao，DuWeiqiang

(School of Civil Engineering & Architecture, Northeast Petroleum University, Daqing 163318, China)

This paper is a research on the effect of transverse connection damage on transverse load distribution of T beam bridge. The study consists of establishing the finite element models by the division of 9 working conditions according to the different positions and forms of damage; producing the transverse load distribution values of main beams under 9 working conditions, using a calculation and analysis method; and comparing the values with those damage-free ones. The results demonstrate that the transverse connection damage triggers the transverse load redistribution, with a resultant change in the transverse load distribution values of each main beams—a change which exhibits an increasing magnitude due to the damage degree; the transverse connection damage is followed by the occurrence of a significantly increased value culminating into a maximum value, in the transverse load distribution of main beams directly acted on by loads shows; the transverse connection damage is accompanied by both an increased values in the transverse load distribution of main beam subjected to load on the one side and a decreased value on the other side, as is shown by the damage point as the borderline. This research highlighting a rule underlying the change in transverse load distribution under transverse connection damages may provide a theoretical reference for T bridge reinforcement and maintenance.

transverse connection; T beam bridge; transverse load distribution; finite element method

2016-10-26

李 科(1975-)，女，黑龙江省肇东人，副教授，硕士，研究方向：体外预应力加固简支梁，E-mail:1023267433@qq.com。

10.3969/j.issn.2095-7262.2016.06.022

U448.2； TU311

2095-7262(2016)06-0695-05

:A