应力敏感低渗透气藏不稳定渗流特征研究

张小龙 杨志兴 时 琼 李 宁 陈 蠡

中海石油(中国)有限公司上海分公司， 上海 200335



应力敏感低渗透气藏不稳定渗流特征研究

张小龙 杨志兴 时 琼 李 宁 陈 蠡

中海石油(中国)有限公司上海分公司， 上海 200335

应力敏感效应普遍存在于低渗透气藏开发过程中。为了研究应力敏感条件下低渗透气藏不稳定渗流特征，在考虑渗透率应力敏感效应的基础上，建立了低渗透气藏不稳定渗流模型，通过模型求解和Stehfest数值反演方法获得了模型的实空间解，在此基础上实例分析了应力敏感对无限大边界、封闭边界及定压边界低渗透气藏不稳定渗流压力动态特征的影响。研究结果表明，井底压力与应力敏感的影响关系是相互的，井底压力越低，应力敏感的影响越为显著；反之，应力敏感的增强加快了井底压力的降低，应力敏感对低渗透气藏渗流的影响不能忽视。研究成果对应力敏感气藏的试井分析和现场生产指导具有一定实用价值。

应力敏感；低渗透气藏；渗流模型；压力动态

0 前言

应力敏感效应普遍存在于低渗透气藏开发过程中，其对低渗透气藏非线性渗流规律的影响不能忽略。国内外很多学者通过理论研究和实验手段对应力敏感的形成机理、影响因素及其对气井稳态产能的影响等研究较多[1-15]，对考虑应力敏感效应的低渗透气藏不稳定渗流的研究甚少。笔者在考虑孔隙度和渗透率应力敏感效应基础上，建立了低渗透气藏不稳定渗流模型，并对模型进行了求解，通过实例分析了应力敏感对无限大边界、封闭边界及定压边界低渗透气藏不稳定渗流压力动态特征的影响，对加深应力敏感效应低渗透气藏不稳定渗流机理的研究与认识有一定借鉴意义。

1 不稳定渗流模型的建立与求解

1.1 模型的建立

渗流基本假设条件如下：

1)储层均质等厚，各向同性，气井以定产量qsc生产；

2)储层中的流体为单相气体，且作平面径向等温渗流，流动服从线性达西定律；

3)孔隙介质可压缩，考虑渗透率和孔隙度的应力敏感；

4)忽略重力、毛管力、井筒储集效应和表皮的影响。

(1)

(2)

式中：φi为原始压力下岩石的孔隙度，无量纲；Cf为岩石的压缩系数，MPa-1。

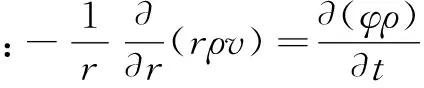
(3)

实验研究表明，渗透率模量可用于描述渗透率与有效应力间的变化关系：

(4)

对式(4)积分得：

k=kie-γ(ψi-ψ)

(5)

将运动方程、状态方程代入连续性方程，并考虑渗透率模量，可以得到考虑渗透率应力敏感影响的低渗透气藏不稳定渗流微分方程：

(6)

1.2 模型的求解

引入无因次拟压力、无因次时间及无因次渗透率模量，将无因次变量代入渗流微分式(6)，并加上定解条件，可得到考虑应力敏感效应的不稳定渗流数学模型：

(7)

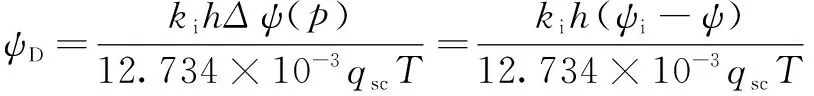
式(7)是一个非线性很强的偏微分方程，需进行线性化处理，通过引入Pedrosa变换化简方程[16]：

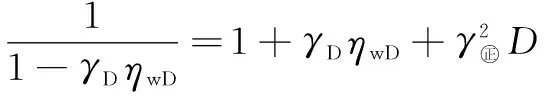
再考虑到较小无因次渗透率模量，只要取零阶摄动解即可，于是渗流数学模型(7)式化为：

(8)

对式(8)进行Laplace变换，可得其Laplace空间解：

(9)

式中：K0、K1分别为零阶、一阶修正贝塞尔函数，无量纲；u为Laplace变量，无量纲。

无限大低渗透气藏井底无因次压力拉氏空间解为：

(10)

式中：L-1为Laplace逆变换，无量纲；O(γD)为ηWD零阶解以上的余量，无量纲。

圆形封闭低渗透气藏井底无因次压力拉氏空间解为：

(11)

(12)

(13)

(14)

圆形定压低渗透气藏井底无因次压力拉氏空间解为：

(15)

(16)

(17)

(18)

2 不稳定渗流压力动态特征

利用Stehfest数值反演算法，将Laplace空间解反演变换得到实空间解[17-20]，通过无因次变量函数的反算，绘制井底压力与时间的半对数曲线及地层压力分布曲线，分析应力敏感对不同外边界低渗透气藏不稳定渗流的压力动态特征。

气藏基本参数为：气井产量8 000 m3/d，绝对渗透率0.7×10-3μm2，储层有效厚度10 m，井筒半径0.1 m，原始地层压力10 MPa，孔隙度0.12，综合压缩系数0.1 MPa-1，气体临界压力4.8 MPa，临界温度200 K，储层平均温度363.5 K，气体相对密度0.62。

图1是应力敏感对无限大低渗透气藏井底压力影响的半对数曲线。从图1可知，随着生产的不断进行，井底压力不断降低，应力敏感的影响越来越显著，流动状态为无限大地层径向流动。应力敏感致使储层的渗透率降低，气体渗流阻力增大，因此，当气井以恒定产量生产时，在某个固定的生产时刻考虑应力敏感影响时的井底压降要高于不考虑应力敏感时的井底压降。同时，从渗透率模量γ对无限大低渗透气藏井底压力影响的半对数曲线(图2)可以看出，应力敏感的影响在晚期井底压力较低的情况下更为显著，γ越大，应力敏感影响越显著，井底压力越低。

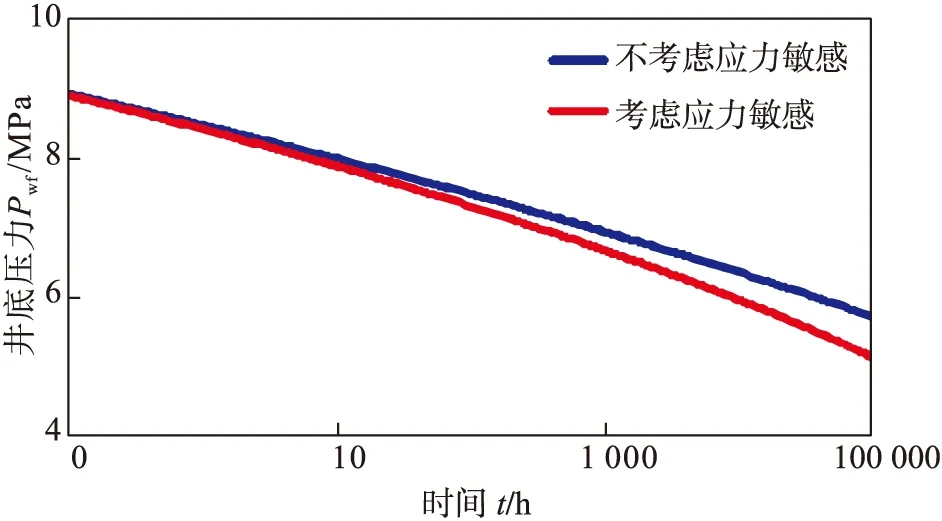
图1 应力敏感对无限大低渗透气藏井底压力影响的半对数曲线

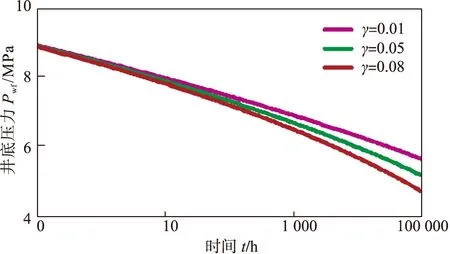
图2 渗透率模量 γ对无限大低渗透气藏井底压力影响的半对数曲线

图3是应力敏感对圆形封闭低渗透气藏井底压力影响的半对数曲线。从图3可知，在压力波传播到封闭边界之前，井底压力不断降低，流动与无限大地层径向流动情形一致，表现为无限作用径向流动阶段；当压力波传播到封闭边界时，无限作用径向流动阶段结束，由于受封闭外边界的影响，井底压力下降速度加快。考虑应力敏感影响时，固定时间点的井底压力低于不考虑应力敏感时的井底压力，压力波到达边界的时间略为延迟，低压开采时间减少。同时，从渗透率模量γ对圆形封闭低渗透气藏井底压力影响的半对数曲线(图4)可以看出，γ越大，应力敏感影响越显著，井底压力下降越快，压力波传播到封闭边界的时间越长。

图3 应力敏感对圆形封闭低渗透气藏井底压力影响的半对数曲线

图4 渗透率模量 γ对圆形封闭低渗透气藏井底压力影响的半对数曲线

图5是应力敏感对圆形定压低渗透气藏井底压力影响的半对数曲线。从图5可知，在压力波传播到定压边界之前，井底压力不断降低，表现为无限作用径向流动阶段，当压力波传播到外边界后，由于受到定压边界的影响，流动达到稳定，井底压力与时间无关，保持恒定值，进入稳定流动阶段，在半对数图上出现水平直线段。考虑应力敏感影响时，压力波传播到边界后的稳定井底流压低于不考虑应力敏感时的井底流压。同时，从渗透率模量γ对圆形定压低渗透气藏井底压力影响的半对数曲线(图6)可以看出，γ越大，应力敏感影响越显著，井底压力越低，压力波传播到定压边界的时间越长，稳定的井底压力越低。

图5 应力敏感对圆形定压低渗透气藏井底压力影响的半对数曲线

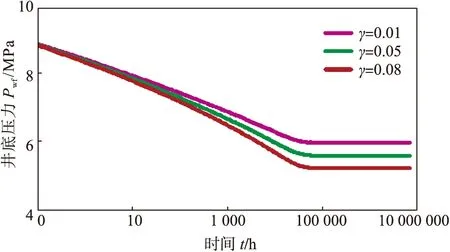
图6 渗透率模量γ对圆形定压低渗透气藏井底压力影响的半对数曲线

图7是渗透率模量γ对无限大低渗透气藏地层压力分布影响的半对数曲线。从图7可知，越靠近井底，不同应力敏感系数下的压降曲线的间距越大，说明应力敏感对地层压力的影响主要集中在近井地带。应力敏感系数越大，地层压力分布的压降漏斗越陡，地层能量损失越强，井底压力越低。

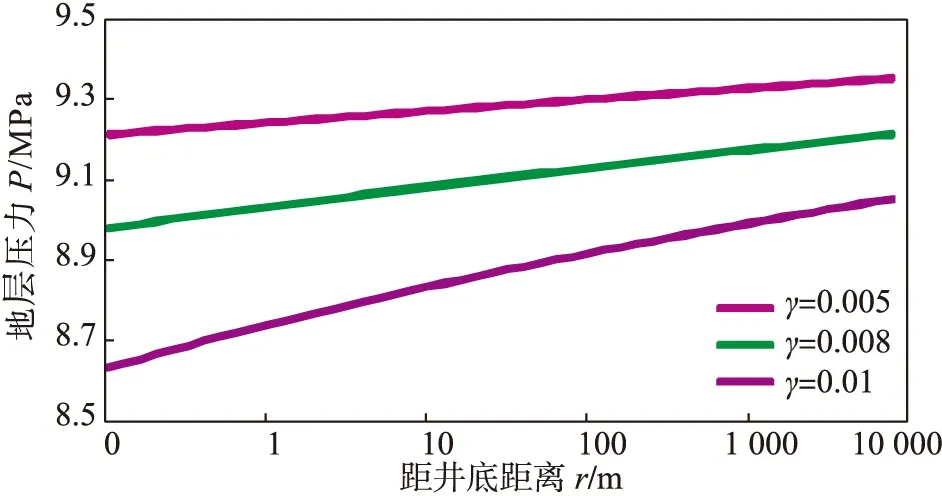
图7 渗透率模量γ对无限大低渗透气藏地层压力分布影响的半对数曲线

3 结论

1)建立了考虑应力敏感效应的低渗透气藏不稳定渗流模型，对模型进行了求解，得到了Laplace空间解析解，利用Stehfest数值反演方法求得了不稳定渗流模型的实空间解，实例分析了应力敏感效应对无限大边界、封闭边界及定压边界低渗透气藏不稳定渗流压力动态特征的影响。

2)研究结果表明，井底压力与应力敏感的影响关系是相互的，井底压力越低，应力敏感的影响越为显著，反之，应力敏感的增强加快了井底压力的降低，应力敏感对低渗透气藏渗流的影响不能忽视。在油气田实际生产过程中，应制定合理的生产工作制度，确定合理的生产压差，尽量减少应力敏感对气田开发的影响，以保证气井的高产、稳产。

[1] 阮 敏，王连刚.低渗透油田开发与压敏效应[J].石油学报，2002，23(3)：73-75. Ruan Min， Wang Liangang. Low-Permeability Oilfield Development and Pressure-sensitive Effect [J]. Acta Petrolei Sinica， 2002， 23 (3)： 73-75.

[2] 杨胜来，肖香娇，王小强，等.异常高压气藏岩石应力敏感性及其对产能的影响[J].天然气工业，2005，25(5)：94-95. Yang Shenglai， Xiao Xiangjiao， Wang Xiaoqiang， et al. Stress Sensitivity of Rock and its Influence on Productivity for Gas Reservoirs with Abnormal High Pressure [J]. Natural Gas Industry， 2005， 25 (5)： 94-95.

[3] 张 政，程林松，廉培庆，等.应力敏感油藏压裂直井分区模型[J].特种油气藏，2010，17(5)：77-80. Zhang Zheng， Cheng Linsong， Lian Peiqing， et al. Divisional Model of Fractured Vertical Well in Stress Sensitive Reservoir [J]. Special Oil & Gas Reservoirs， 2010， 17 (5)： 77-80.

[4] 张小龙，李晓平，曹丽娜，等.考虑压敏效应的气井产能预测新方法[J].海洋石油，2013，33(1)：69-71. Zhang Xiaolong, Li Xiaoping, Cao Lina， et al. A New Method for Forecast the Productivity of Gas Well under the Consideration of Pressure Sensitive Effect [J]. Offshore Oil， 2013， 33 (1)： 69-71.

[5] 杨 彬，侯大力，龙 刚，等.低渗透储层应力敏感实验研究及应用[J].油气藏评价与开发，2012，2(5)：41-45. Yang Bin， Hou Dali， Long Gang， et al. Research and Application of Stress Sensitive Experiment on Low Permeable Reservior [J]. Reservoir Evaluation and Development, 2012， 2 (5)： 41-45.

[6] 温伟明，朱绍鹏，李 茂.海上异常高压气藏应力敏感特征及产能方程—以莺歌海盆地为例[J].天然气工业，2014，34(9)：59-62. Wen Weiming， Zhu Shaopeng， Li Mao. Stress Sensitivity Features and Productivity Equations of Offshore Abnormal High-pressure Gas Reservoirs: A Case Study from the Yinggehai Basin [J]. Natural Gas Industry, 2014， 34 (9)： 59-62.

[7] 方 洋.气藏产能应力敏感性研究[J].油气井测试，2009，18(6)：18-20. Fang Yang. Research on Relationship between Deliverability of Gas Reservoir and the Stress-Sensitiveness of the Reservoir [J]. Well Testing， 2009， 18 (6)： 18-20.

[8] 戈尔布诺夫.异常油田开发[M].张树宝，译.北京:石油工业出版社，1987:6-14. Gorbunov A T. Abnormal Oilfield Development [M]. Zhang Shubao， trans. Beijing: Petroleum Industry Press， 1987: 6-14.

[9] 曾 杨，贺陆军，廖剑波，等.应力敏感性低渗透气藏垂直裂缝井非达西渗流产能分析[J].特种油气藏，2012，19(5)：90-96. Zeng Yang， He Lujun， Liao Jianbo， et al. Productivity Analyses of Non-Darcy Permeable Flow in Stress-sensitivity and Low-permeability Gas Reservoirs with Vertical Fractures [J]. Special Oil & Gas Reservoirs, 2012， 19 (5)： 90-96.

[10] 霍凌婧.火山岩气藏复杂渗流机理研究[D].北京:中国科学院研究生院(渗流流体力学研究所)，2009. Huo Lingjing. Complex Mechanics of Flow in Volcanic-rock Gas Reservoir [D]. Beijing: Graduate School of Chinese Academy of Sciences (Seepage Fluid Mechanics Research Institute)， 2009.

[11] 安志斌，贾爱林，位云生，等.考虑应力敏感的异常高压气藏产能新方程[J].石油天然气学报，2013，35(11)：141-143. An Zhibin， Jia Ailin， Wei Yunsheng， et al. A New Method of Deliverability Equation Considering Stress Sensitivity in Abnormal Pressure Gas Reservoirs [J]. Journal of Oil and Gas Technology， 2013， 35 (11)： 141-143.

[12] 刘之的，苗福全，罗晓芳，等.火山岩裂缝型储层应力敏感性实验研究[J].天然气地球科学，2012，23(2):208-212. Liu Zhidi， Miao Fuquan， Luo Xiaofang， et al. Experiment of Stress Sensitivity for Igneous Fractured Reservoir [J]. Natural Gas Geoscience， 2012， 23 (2): 208-212.

[13] 薛定谔.多孔介质中的渗流物理[M].王鸿勋，译.北京:石油工业出版社，1982:26-33. Schrodinger A E. Translated Porous Media Flow Physics [M]. Wang Hongxun， trans. Beijing: Petroleum Industry Press， 1982: 26-33.

[14] 于忠良，熊 伟，高树生，等.致密储层应力敏感性及其对油田开发的影响[J].石油学报，2007，28(4):95-98. Yu Zhongliang， Xiong Wei， Gao Shusheng， et al. Stress Sensitivity of Tight Reservoir and its Influence on Oilfield Develop-

ment [J]. Acta Petrolei Sinica, 2007， 28 (4): 95-98.

[15] 兰 林,康毅力,陈一健,等.储层应力敏感性评价实验方法与评价指标探讨[J].钻井液与完井液，2005，22(3)：1-4. Lan Lin, Kang Yili, Chen Yijian, et al. Discussion onEvaluation Methods for Stress Sensitivities of Low Permeability and Tight Sand Stone Reservoirs [J]. Drilling Fluid & Completion Fluid， 2005， 22 (3)： 1-4.

[16] Pedrosa O A. Pressure Transient Response in Stress-sensitive Formations [C]//Paper 15115 Presented at the SPE California Regional Meeting， 2-4 April 1986， Oakland， California， USA. New York: SPE， 1986.

[17] Stehfest H. Numerical inversion of Laplace transform [J]. Communication of the ACM， 1970， 13 (1): 47-49.

[18] 贾永禄，赵必荣.拉普拉斯变换及数值反演在试井分析中的应用[J].天然气工业，1992，12(1):60-64. Jia Yonglu， Zhao Birong. Application of Laplace Transform and Numerical Inversion to Well Test-analysis [J]. Natural Gas Industry， 1992， 12 (1): 60-64.

[19] 姜 永，王新海，袁恒龙，等.低孔多裂缝气藏不稳定渗流分析[J].天然气与石油，2011,29(6)：59-60. Jiang Yong， Wang Xinhai， Yuan Henglong， et al. Analysis on Unsteady Seepage in Non-porous and Multi-fracture Gas Reservoir [J]. Natural Gas and Oil， 2011， 29 (6)： 59-60.

[20] 贾永禄，孙高飞，聂仁仕，等.基于应力敏感性的视均质火山岩气藏试井模型[J].天然气与石油，2015，33(4):33-35. Jia Yonglu， Sun Gaofei， Nie Renshi， et al. Well Test Model for Pseudo-Homogeneous Volcanic Gas Reservoir Based on Stress Sensitivity [J]. Natural Gas and Oil， 2015， 33 (4): 33-35.

2015-08-09

张小龙(1985-)，男，江西吉安人，工程师，硕士，主要从事油气田开发工程方面的生产科研工作。

10.3969/j.issn.1006-5539.2016.01.017