变节距下采煤机行走机构的动力学特性

张 丹， 王爱芳， 陈国晶

(黑龙江科技大学 机械工程学院， 哈尔滨 150022)

变节距下采煤机行走机构的动力学特性

张 丹， 王爱芳， 陈国晶

(黑龙江科技大学 机械工程学院， 哈尔滨 150022)

针对采煤机行走轮与销齿复杂的啮合特性导致的行走轮经常发生断齿，以及非正常磨损等失效状况，采用相对运动理论和牛顿第二运动定律，研究行走机构行走轮-销齿、齿轨-齿轨弹性连接的力学模型，给出销齿啮合力表达式，建立采煤机行走机构的动力学方程；采用动力学仿真法，得到行走轮角速度、销齿啮合力变化曲线及节距变化曲线。研究表明：节距变化对销齿啮合力和速度波动影响显著；销齿啮合力最大峰值出现在两节齿轨连接处附近，且该区域行走轮速度波动最频繁，齿轨节距最小时，行走轮速度波动值较小，仅为2%；销齿节距最小值为143 mm，最大值为158.5 mm。该结果对研究采煤机行走机构动力学特性、改善行走轮及齿轨受力、提高行走轮使用寿命具有一定参考价值。

行走机构； 动力学特性； 变节距； 弹性模型

0 引 言

在采煤机行走机构中，由于受到采煤机滚筒负载作用，其工作过程中受到很大程度的偏载，因此当导向滑靴磨损到一定程度后，导向作用减弱，使得行走轮与齿轨往往不能正确啮合[1-2]。此时，行走轮轮齿会产生很大冲击，采煤机牵引力只能由另一个牵引部提供，加剧了行走机构及整机的振动，使行走轮与销齿的啮合特性呈现出更为复杂的动态变化[3]。由于井下条件限制，采煤机正常工矿下各种实验很难进行，因此，动力学仿真分析及数值分析成为研究行走机构动态特性的主要方法。国内众多学者对行走机构的动态特性进行深入的研究，认为销齿啮合产生冲击的主要原因是销齿节距过小[4-5]。还有研究将牵引负载考虑为恒转矩，不考虑销排连接处节距的动态变化特性。这使所得到的行走机构的丢失了许多重要信息，无法准确描述行其动态特性。笔者以实验获得的截割负载作为原始数据，并考虑两节齿轨连接处的节距变化，通过构建含齿轨间隙的行走机构弹性模型，得到行走机构动力学方程，对其进行求解，最后采用动力学仿真的方法，进行行走机构动力学特性的研究。

1 变节距下行走机构的动力学模型

以某采煤机渐开线行走轮及节距为147 mm的Ⅲ型销齿为研究对象，建立含齿轨间隙的行走机构弹性模型，图1为行走轮与销齿啮合结构，其啮合过程类似于齿轮齿条啮合。

为适应底板的不平整及输送机的弯曲，齿轨间采用元宝座连接，同时允许连接处水平与垂直方向存在一定的弯曲角度，这使齿轨的节距在不断变化，导致行走轮在经过齿轨连接处受到冲击载荷，传统的纯刚性模型很难描述齿轨节距发生变化时行走机构的动态特性[6]。为此，除了考虑行走轮轴自身的弹性变形及行走轮与销齿接触处的弹性变形外，还必须考虑齿轨之间的弹性连接。为便于分析系统的运动特性，假设垂直牵引方向的支撑系统刚度足够，由相对运动理论，假设行走轮做定轴转动，则齿轨相对底板水平移动，取两节齿轨作为研究对象，得到采煤机行走机构的动力学模型，如图2所示。图2中，M为电机输入扭矩，rb为行走轮基圆半径，kv为销齿副综合啮合刚度，cv为销齿副啮合阻尼系数，kw为行走轮轴沿着牵引方向的弯曲刚度，cw为行走轮轴沿着牵引方向的弯曲阻尼系数，kl为齿轨间连接刚度，cl为齿轨连接阻尼系数。

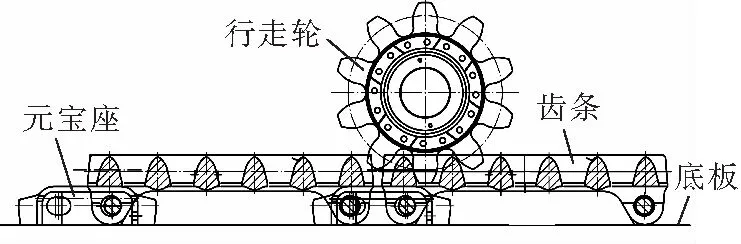
图1 采煤机行走轮与销齿啮合

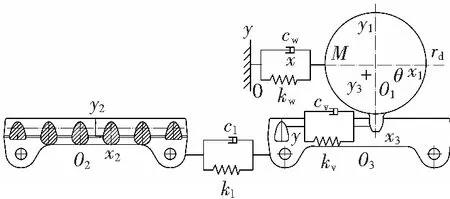
图2 含齿轨间隙的行走机构动力学模型

2 动力学方程及求解

2.1 动力学方程的建立

如图2所示，行走轮中心处建立总体坐标系O-xyz，在行走轮回转中心及两节齿轨几何中心处分别建立随刚体一起运动的局部坐标系O1-x1y1z1、O2-x2y2z2、O3-x3y3z3。假设采煤机匀速行驶，θ为行走轮转角，x1为行走轮轴沿牵引方向振动位移，x2、x3分别为两节齿轨沿牵引方向位移，取θ、x1、x2、x3为系统广义坐标，根据牛顿第二运动定律[7]，建立系统的动力学方程，有

(1)

式中：m1、m2——行走轮和单节齿轨质量，kg； Fv——销齿动态啮合力，N； J——行走轮转动惯量，kg·mm2。

2.2 销齿传动的啮合力

行走系统除了受到外部的振动激励外，在齿轮及销齿啮合过程中还会产生内部的动态激励。销齿传动过程类似于齿轮齿条传动过程，动态激励是系统振动的根源，主要包括刚度激励、啮合冲击激励和误差激励[7]。

(1)刚度激励

如果把销齿副看做沿啮合线方向的弹簧，弹簧刚度的变化必然引起啮合力的变化。刚度激励是由于啮合过程中重合度变化引起的。一般情况下，销齿传动的重合度1≤ε≤2，当销齿法向节距小于行走轮法向节距时，啮合重合度小于1，在啮合过程中一对齿与两对齿交替啮合，销齿传动综合啮合刚度可表示为

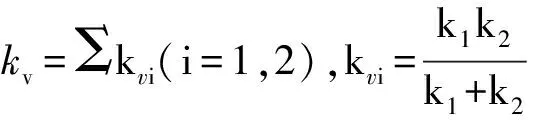
(2)

式中：kvi——第 对销齿的综合啮合刚度，N/mm；

k1、k2——行走轮、销齿啮合点法向的啮合刚度，N/mm。

两对销齿啮合刚度的变化如图3所示，图3中Δ为一对轮齿啮合时间。实际进行分析时，将此曲线简化为矩形波[8]。

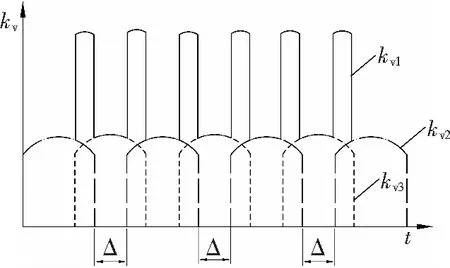
图3 两对轮齿啮合刚度

(2)啮合冲击激励

行走轮制造过程中产生的基节误差和销齿啮合时的弹性变形会产生啮合冲击，啮合冲击属于瞬间行为，是一种动态载荷激励，用常规方法很难定量确定啮合冲击激励f(t)，可通过有限元方法模拟的齿轮传动内部的啮合冲击激励近似代替[9-10]。

(3)误差激励

误差激励主要是由行走轮以及齿轨的几何误差引起的。由于采煤机行走部为开式传动系统，行走轮与齿轨之间夹杂大量煤粉与煤块，销齿啮合处接触精度不高，所以，误差激励不容忽视。图4所示是一种位移激励[11]，与接触点处弹性变形量有关，其转角长周期误差为一近似正弦曲线，短期误差可用傅里叶级数表示：

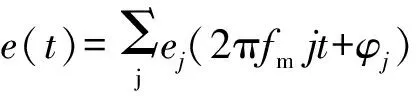
(3)

式中：ej、φj——第j阶分量的幅值和相位；

fm——啮频。

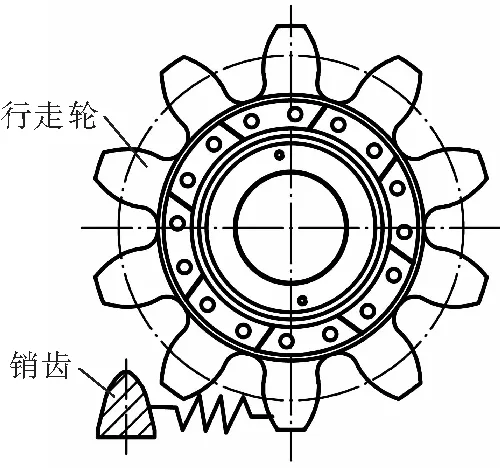
图4 误差激励

(4)啮合阻尼系数

行走轮轮齿的啮合阻尼系数

(4)

式中：me——销齿副的当量质量，kg；

ξ——啮合阻尼比，实验表明，其值为0.03～0.17[12]。

行走轮轴的弯曲阻尼系数

(5)

式中：me——行走轮输入端转动惯量，kg·mm2；

ξw——弯曲阻尼比，其值为0.03～0.1[13]。

销齿传动中，第i个齿对在啮合点处的法向啮合力为

Fi=kviδi,

(6)

式中：δi——齿对i在啮合点位置的综合变形，mm；其值与齿部的弯曲与剪切变形、齿根弹性引起的附加变形及啮合点的接触变形有关[14]。

(5)销齿啮合力

用ei表示第i对齿的齿廓误差，则δi=θrd-x1-ei,销齿啮合力可表示为

(i=1,2),

(7)

式中：cvi——第i对销齿的综合啮合阻尼。

2.3 动力学方程求解

(1)行走机构动力学方程

将方程组(1)整理为矩阵形式，得到采煤机行走机构动力学方程

Mq+Cq+Kq=P,

(8)

式中：q=(θ x1x2x3)T；

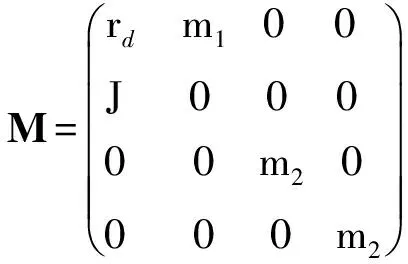
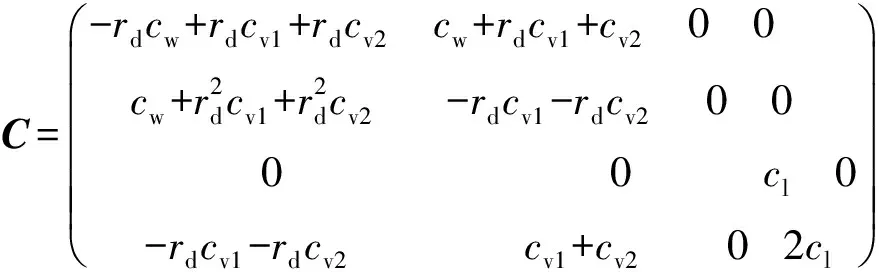
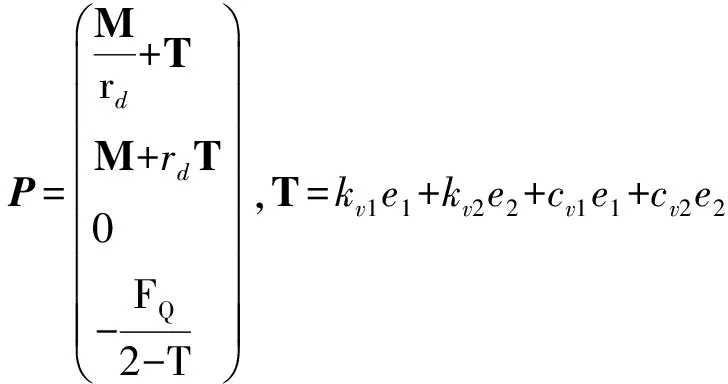
(2)秩1拟Newton法

对于非线性方程组F(x)=0,F(x)=(f1,f2,…,fn)T,x=(x1,x2,…,xn)T，有

(9)

F(x)的Jacobi矩阵在xi之值。

为避免每步都重新计算Ai，采用类似于割线法的思路，只要求新的Ai+1，使其满足方程

Ai+1(xi+1-xi)=F(xi+1)-F(xi),i=0,1,…,n。

(10)

由式(10)可知，当n=1时，矩阵Ai+1为F关于点xi及xi+1的差商，当n>1时，Ai+1并不确定，为此，限制Ai+1是由Ai的一个低秩修正矩阵得到的，即

Ai+1=Ai+ΔAi，rank(ΔAi)=m≥1，

(11)

式中：ΔAi,——秩为m的修正矩阵。

计算时，只需对给出的初始近似x0及矩阵A0，用式(9)～(11)逐次计算得到{xi}及{Ai}，从而避免每步都要计算F的Jacobi矩阵。

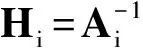
(12)

可见，式(12)不用求逆就能逐次推算出{Hi}。

当rank(ΔAi)=rank(ΔHi)=1时，设

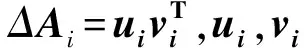
(13)

式中：ui、vi待定。

记ri=xi+1-xi,yi=F(xi+1)-F(xi)，式(10)可写为

Ai+1ri=yi。

(14)

将式(13)代入式(10)，整理得

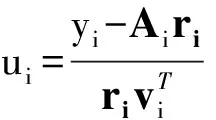
(15)

将式(15)代入式(13)，则有

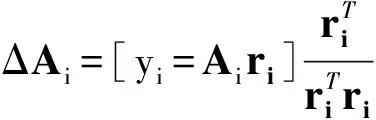
(16)

即

(17)

与式(17)互逆的秩1拟Newton法为

(18)

为方便方程组(8)的求解，将销齿传动的激振力用正弦和余弦函数表示，从而可得到振动方程在时域和频域的解。

3 牵引负载

3.1 截齿截割阻力

利用项目组自主研发的多截齿旋转截割实验台进行截割实验，获得截齿的截割阻力曲线如图5所示。滚筒截割载荷是多个截齿截割载荷共同作用的结果，其在数值上并不是截齿截割载荷的叠加，但其变化规律与单截齿截割载荷变化规律相似，因此，可以利用实验获得的载荷规律近似模拟滚筒截割负载[15]。

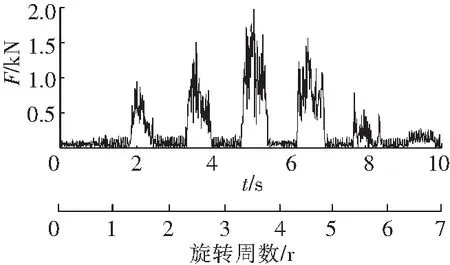
图5 截齿截割载荷测试曲线

3.2 牵引负载的确定

由于煤层往往具有一定倾角，因此采煤机牵引力方向与行走速度方向存在一定夹角，将牵引力分解为沿行走方向的牵引力与垂直于行走方向的牵引力，沿牵引速度方向的分量属于有效牵引力。因此实际工作中，牵引机构并不时刻在额定牵引力下工作。采煤机牵引力计算较为复杂，理论上，采煤机牵引移动必须克服滚筒所受牵引阻力及牵引系统水平方向的所有外力，考虑整机存在的振动及其它不确定工况，取1.25倍的安全系数，根据整机受力分析，有[16]

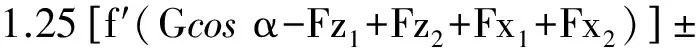
(19)

式中：Fx1、Fx2——前后滚筒侧向阻力，N；Fz1、Fz2——前后滚筒截割阻力，N；Fy1、Fy2——前后滚筒轴向阻力，N。

采煤机工作时，后滚筒截割厚度小于前滚筒，其截割载荷可按照80%前滚筒截割载荷来计算。假设煤层倾角为10°，整机重量约150 t，截齿楔入角为45°，取牵引阻力系数Ka=0.6，摩擦因数f=0.18[17-19]。为得到更为准确的动力学分析结果，考虑滚筒的真实截割负载，将截割载荷测试曲线作为已知条件，滤掉曲线中的高频信号，根据截齿三向力数学关系，将数据代入式(19)，并将得到的牵引载荷曲线进行分段拟合，牵引阻力曲线,如图6所示。

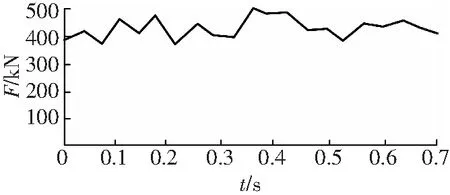
图6 牵引负载曲线

4 行走机构动力学仿真

4.1 仿真参数设置

仿真模型使用摆线轮和Ⅲ型销齿，标准节距为147 mm。定义齿轨间弹簧阻尼力，用以模拟齿轨间距的变化，其具体参数：接触刚度为5×105N/m,接触系数H，接触阻尼5×103N·s/mm,穿透深度0.01 mm，静摩擦因数0.11，动摩擦因数0.1，静摩擦转变速度0.2 mm/s，动摩擦转变速度0.5 mm/s。销齿之间添加碰撞接触力，碰撞刚度采用函数进行描述，函数曲线如图3所示，其最大值为5×105N/mm，啮合冲击激励和误差激励采用穿透深度综合描述，其值为0.005 mm[2]。以某型号采煤机截割工况为例，其滚筒转速为40.8 r/min，行走速度为3.7 m/s，则其单周截割周期约为0.7 s，行走轮通过一节齿轨时长为2.38 s，为获得行走轮经过销排连接处的动态特性，需将上述得到的牵引力作用时间呈周期倍进行外推。以行走轮与第一个销齿相接触作为初始时刻，选取仿真时间5 s，仿真步长500[2]，对模型进行仿真。

4.2 仿真结果分析

行走轮速度波动曲线及行走轮与齿轨动态接触力仿真结果如图7、8所示。

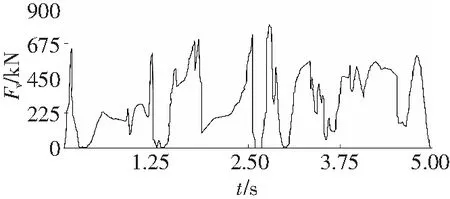
图7 行走轮与齿轨动态啮合力仿真结果

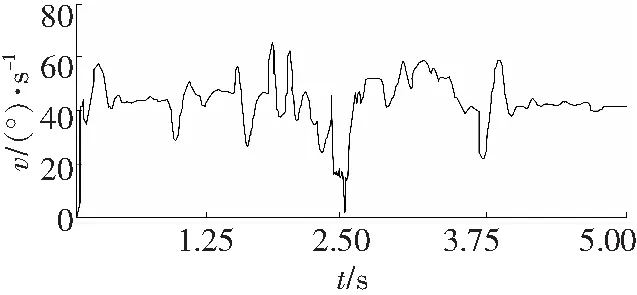
图8 行走轮速度波动曲线

由图7可以看出，行走轮与齿轨初始啮合时产生了较大的瞬时冲击，理想情况下，2.38 s行走轮与第一节齿轨脱离接触，但由于弹簧阻尼作用，其啮合冲击存在一定的滞后，2.57 s时行走轮与第二节齿轨接触，行走轮在脱离第一节销排以及进入第二节销排期间，均出现了较大的冲击，且在进入第二节销排后出现了频率更高的冲击情况。4.9 s后行走轮速度趋于稳定，销齿啮合力为0。这是因为4.9 s后行走轮与第二节齿轨脱离，行走轮空转。虽然销齿啮合力多次出现峰值，但最大峰值出现在两节齿轨连接处附近。在销齿啮合过程中多次出现啮合力瞬态为零的情况，这是因为行走轮与齿轨并不是共轭啮合，多次发生分离，进而产生多次碰撞，这与实际情况相符[18]。行走轮在与销齿啮合时，啮合力恒为非负值，这说明虽然行走轮速度波动频繁，但不存在齿廓非工作面啮合冲击的情况。

节距变化对行走轮速度波动影响显著，行走轮速度突变主要出现在初始接触瞬间及节距变化处，在齿轨连接区域，行走轮速度波动最频繁，在与第二节齿轨初始啮合时，角速度波动值最大。

图9为两节齿轨连接处的节距变化曲线。可以看出，当行走轮与第一节齿轨接触时，对其产生一定的冲击，其与第二节齿轨产生一定的相对运动，因此齿轨节距也在不断变化，当行走轮与第二节齿轨接触后，齿轨节距明显变大，之后又逐渐减小；当两节齿轨节距等于标准节距时，行走轮速度波动虽然频繁，但波动值较小。由上述曲线可知，齿轨节距变化对销齿啮合力及行走轮速度波动影响显著，改变齿轨连接处节距值，进行多次仿真，根据仿真数据，得到销齿啮合力及行走轮速度波动峰值随齿轨节距的变化情况如表2所示。由表1可知，无论节距变大还是减小，都会导致销齿间啮合力峰值增加，对销齿的受力都是不利的，节距越小，啮合力峰值越大，但节距变大时销齿啮合力峰值增加并不明显，说明大节距时销齿的受力状态优于小节距受力状态；节距过小会导致销齿啮合重合度减小，当节距小于143 mm时，会产生销齿啮合悬空的情况，此时，牵引负载只由一个行走轮承担，极易造成行走轮断齿现象；随着节距增大，行走轮速度波动增加，当节距大于158.5 mm时，行走轮与销齿无法啮合。

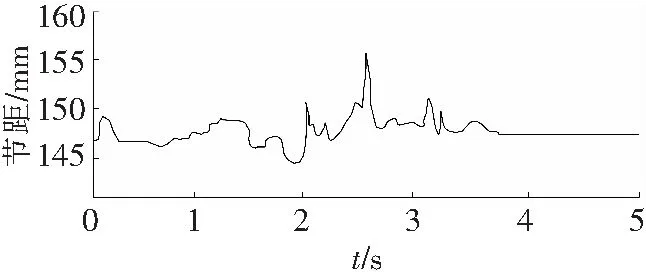
图9 两节齿轨连接处节距变化曲线

表2 啮合力及速度波动峰值随齿轨节距变化情况

5 结 论

(1) 齿轨节距变化对销齿啮合力及行走轮速度波动影响显著，考虑行走轮与销排啮合时齿面的弹性变形和销排连接处的间距变化，建立行走机构力学模型与仿真模型，分析销齿传动过程的动态激励，确定动力学方程中的阻尼系数，给出销齿啮合力的数学表达式。

(2) 给出行走机构动力学方程的求解方法，根据牵引负载与滚筒各阻力的经验公式，利用截割阻力实验曲线及截齿三向力的关系，得到了牵引阻力的分段拟合曲线，并将其作为牵引负载进行了行走机构动力学仿真分析。

(3) 对变节距下行走机构动力学特性进行了仿真研究，仿真结果表明：销齿啮合力最大峰值出现在两节齿轨连接处附近，变节距下，齿轨连接区域行走轮速度波动最为频繁，但波动幅值不大。得到销齿节距的变化范围，其最小值为143 mm，最大值为158.5 mm，节距小于143 mm时，牵引负载由一个行走机构承担，容易造成行走轮断齿，节距大于158.5 mm时，行走轮与销齿无法啮合。齿轨节距越大，行走轮速度波动峰值越大，节距越小，销齿啮合力峰值越大，齿轨节距最小时，行走轮速度波动值较小，仅为2%。

[1] 刘春生， 任春平， 李德根. 修正离散正则化算法的截割煤岩载荷谱的重构与推演[J]．煤炭学报， 2014(5): 981-986．

[2] 张 丹， 田 操， 孙月华． 销轨弯曲角对采煤机行走机构动力学特性的影响[J]． 黑龙江科技大学学报， 2014， 24(3): 262-266.[3] 赵丽娟， 刘旭南， 马联伟．基于经济截割的采煤机运动学参数优化研究[J]． 煤炭学报， 2013(8): 1490-1495.

[4] 李晓豁, 葛怀挺． 连续采煤机截齿随机载荷的数学模型[J]． 中国工程机械学报， 2006(3): 262-264.

[5] ZHANG DAN, HU SHENGHAI, LIU CHUNSHENG. Elastic model of shearer walking mechanism and traction characteristics[J]. International Journal of Applied Mathematics and Statistics, 2013, 51(4): 462-472.

[6] 刘春生， 于信伟， 任昌玉． 滚筒式采煤机工作机构[M]． 哈尔滨: 哈尔滨工程大学出版社， 2010.

[7] 李德根,刘春生. 镐型截齿截割煤岩动力系统的混沌特征[J]. 黑龙江科技学院学报, 2011, 21(6): 458-462.

[8] 毛 君， 张 瑜， 刘占胜，等．刨头间隙碰撞载荷下滑架体疲劳寿命试验分析[J]．工程设计学报， 2016(2): 160-165.

[9] 石照耀， 康 焱， 林家春．基于齿轮副整体误差的齿轮动力学模型及其动态特性[J]． 机械工程学报， 2010， 17 (7): 55-61.[10] 张 靖， 陈兵奎， 康传章．计及齿面摩擦的直齿轮动力学分析[J]． 振动与冲击， 2012, 21(2): 126-132.

[11] 刘春生, 王庆华, 任春平. 镐型截齿载荷谱定量特征的旋转截割实验与仿真[J]. 黑龙江科技大学学报, 2014， 24(2): 195-199.[12] ZHANG DAN, HU SHENGHAI, LIU CHUNSHENG. Elastic Model of Shearer Walking Mechanism and Traction Characteristics[J]. Joural of Applied Mathematics and Statistics, 2013, 51 (12): 442-453.

[13] ZHANG DAN，HU SHENGHAI，LIU CHUNSHENG．Modeling and Kinematics Simulation of Shearer’s Travelling Mechanism Based on Virtual Prototyping Technology[C]// ICAMMP2012： Applied Mechanics and Materials：396-399.

[14] ZHAO L, LAN J. Dynamic simulation for transmission system of coal winning machine cutting part[J]. Journal of Vibration and Shock, 2014, 33(3): 106-110.

[15] 任春平,刘春生. 煤岩模拟材料的力学特性[J]. 黑龙江科技大学学报, 2014,24(6):581-584.

[16] 刘春生． 滚筒式采煤机理论设计基础[M]．徐州: 中国矿业大学出版社， 2003.

[17] 刘春生， 李德根． 不同截割状态下镐型截齿侧向力的实验与理论模型[J].煤炭学报， 2016， 41(9) : 2359-2366．

[18] 王忠宾， 徐志鹏． 基于粒子滤波的采煤机截割负载特性分析[J]． 煤炭学报， 2011， 36(6)： 696-700.

[19] 吴卫东, 张志飞. 采煤机行走机构啮合参数对动力学特性的影响[J]. 黑龙江科技大学学报, 2014, 24(3): 256-261.

(编辑 晁晓筠 校对 李德根)

Research on dynamic characteristics of walking mechanism behind shearers with varying pitch

ZhangDan，WangAifang，ChenGuojing

(School of Mechanical Engineering,Heilongjiang University of Science & Technology, Harbin 150022,China)

This paper is devoted to overcoming the walking wheel vulnerability to frequent broken teeth resulting from the complex meshing characteristics behind coal shearer walking wheel and pin gear; and eliminating the failure due to abnormal wear. The research using relative motion theory and Newton's second law consists of investigating the mechanics model for elastic connection between the walking wheel and pin gear, rack and rack; providing pin tooth meshing force expression and establishing the dynamics equation of coal running gear; developing the varying curve of the wheel angular velocity, pin tooth meshing force, and the pitch using dynamic simulation method. The research demonstrates that pitch changes have a significant impact on gear meshing force and speed fluctuation and; a walking wheel has a smallest speed fluctuation value, only 2%, such as occurs when the teeth meshing force has a maximum peak occurring near the connection between the two teeth track where a walking wheel experiences a most frequent speed fluctuation, combined with the minimum rack pitch; in this case, pin pitch ranges from the minimum value of 143 mm to the maximum value of 158.5 mm. The results may serve as certain reference for studying the dynamic characteristics of the walking mechanism behind shearers, improving the way walking wheels and racks are subjected to loads, and improving the service life of the walking wheel racks.

walking mechanism; dynamics; varying pitch; elasticity model

2016-10-10

黑龙江省自然科学基金项目(QC2015053)；哈尔滨市科技局创新人才项目(2015RAQXJ017)

张 丹(1982- )，女，黑龙江省哈尔滨人，副教授，博士研究生，研究方向：多刚体系统动力学仿真，E-mail：bishe_2006@163.com。

10.3969/j.issn.2095-7262.2016.06.017

TD421

2095-7262(2016)06-0669-06

:A