基于能力约束的多车种空车动态调整方法

张红斌，董宝田，孙远运

(1.北京交通大学 交通运输学院，北京 100044；2.中国铁路信息技术中心，北京 100844)



基于能力约束的多车种空车动态调整方法

张红斌1,2，董宝田1，孙远运2

(1.北京交通大学 交通运输学院，北京 100044；2.中国铁路信息技术中心，北京 100844)

引入空车时空服务网络来描述铁路运输动态变化特性，同时考虑到实际运输生产中的能力约束，并据此建立了基于能力约束的动态规划模型.模型的目标函数考虑了与时间因素相关的空车滞留费用和需求未满足时的惩罚费用等相关费用，同时考虑了多个车种之间的替代费用.模型的能力约束条件考虑了网络弧段的通过能力、空车提供站的发送空车能力和空车需求站的接收空车能力.考虑网络径路绕行的情况，设计了融合K短路算法的模拟退火算法，并采用了两步法的优化策略进行求解.最后对一个简单的路网进行了验证，结果表明融合K短路算法可以在能力约束条件下得到较好的收益.

铁路运输；能力约束；多车种空车动态调整；时空服务网络；模拟退火算法

铁路空车调整问题是涉及铁路运输资源优化配置的重要问题，不仅是实际生产中的重要内容，同时也是国内外很多学者研究的热点问题.由于空车调配问题本质为一个路网运输问题，因此需对复杂的网络进行简化处理，处理方法主要有区段中心优化法、重心优化法和振荡法等3种[1-3],但是由于路网货流和区段能力的动态变化特性，这些通过固定的方法合并网络具有一定的不合理性，基于此，多个学者进行了深入研究，林柏梁等[4]通过分布优化迭代的算法研究了能力约束条件下的空车调配问题.温旭红等[5]根据多商品网络流理论构建铁路车流分配及径路优化模型，将路径的合理绕行纳入约束体系，使结果更加符合铁路运输实际.曹学明等[6]考虑了滞留费用对于空车调配问题的影响.程学庆等[7]研究了考虑时间因素的空车调配优化问题，约束条件包括时间窗和区段空车运输能力约束.梁栋等[8]采用动态规划方法提出了铁路局管内空车调配的动态优化模型.王龙等[9]研究了全路空车动态调配及路网分界口排空流量测算方法，基于时空网络的概念建立了动态调配优化模型.但是这些成果并没有将多车种和调配的动态特性进行统一研究.

国外通常将重车径路与空车调配协同优化调整作为主要的研究方向.Loxton等[10]设计了动态规划和黄金分割相结合的算法，研究了未来需求不确定的情况下，考虑包含多种车辆类型的车辆规模问题. Yaghini等[11]采用遗传算法和模拟退火算法集成的启发式算法研究了动态多阶段的车辆规模问题.然而此类文章研究的侧重点为购买车辆以及车辆的维护费用，这与空车调整问题研究所关心的费用有所不同，同时研究并没有涉及车种替代问题.

本文作者在前人研究的基础上，结合当前货改对于精细化调度指挥的要求，提出了多车种动态调整的方法，构建了基于能力约束的空车多车种动态调整模型.研究了在路网能力约束的条件下，多种空车在不同的时间阶段内的有效调配，以便产生较好的经济效益，更好地适应铁路部门当前对于调度精细化管理的需求.

1 问题的描述

铁路系统的空车调整问题主要分为排空和配空2种.本文所研究的模型主要用来解决各铁路局的空车配空计划的优化.在实际的生产过程中，由于多种不确定因素，路网的货流和车流情况变化比较频繁，车站生产是通过日班计划和阶段计划结合的方式来适应这种动态变化特性，然而此种方法只是在变化发生的时候被动调整，会导致车站装卸能力使用不均衡；同时，在实际的运输生产中由于某些路段的运输任务比较紧张，主要供重车通行(比如大秦线)，空车需要选择其他的绕行径路，考虑路段为空车预留的能力约束是实际运输生产过程中的需求.因此，本文研究在能力约束下的多阶段空车调整方法，同时考虑路网货流的动态变化特性.

空车时空服务网络的概念是专门针对空车调整模型提出的，如图1所示.它能够比较直观地反映出多阶段空车调整的模式.剩余空车转移弧表示了空车提供点在本阶段剩余的空车滞留到下一个阶段的转移弧，空车分配转移弧表示了空车从提供点配送到需求点的转移弧，不满足空车转移弧表示了空车需求点在本阶段没有满足的空车需求从而累计到下一个阶段的转移弧.

图1展示了4个车站(S1，S2，N1，N2)，2个车辆提供车站(S1，S2)和2个车辆需求车站(N1，N2)，4个时间阶段(T1，T2，T3，T4)的一个空车时空服务网络图.

2 空车调整模型的构建

2.1 模型的假设

空车调整问题的模型假设有：1)对于空车需求站，此阶段不满足的需求，将会叠加到下一个阶段的需求中；2)对于空车提供站，此阶段滞留的空车，将会叠加到下一个阶段的空车中；3)空车需求站和空车提供站的性质在计划周期内不变；4)空车需求站在每个阶段提供的空车数量保持不变，空车提供站在每个阶段需求的空车数量保持不变；5)路网中任意两车站之间车辆的运行时间固定.

2.2 数学模型

2.2.1 变量的定义

N表示网络中所有的站点集合；N1表示网络中所有的空车提供站点集合；N2表示网络中所有的空车需求站点集合；A表示网络中所有的弧段集合；a表示网络中任意一个弧段；k表示网络中任意一个径路；T表示时间阶段集合；t表示任意一个时间阶段；U表示车种集合；u表示任意一种车种.

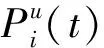
2.2.2 数学模型

(1)

s.t.

∀j,t,u

(2)

∀i,t,u

(3)

∀i,t,u

(4)

∀a,t

(5)

(6)

(7)

∀i,j,t,k,u,v

(8)

目标函数(1)为多目标决策函数，表示空车调配计划的综合收益，包含了空车调配的纯收益最大化，调配费用支出的最小化.费用包含：空走费用、滞留费用、需求未满足的惩罚费用和车种替代费用.

式(2)为空车需求站在某时间段内未满足的空车需求，它等于上阶段和本阶段的未满足空车数量之和.

式(3)为空车提供站在某时间阶段所剩余的空车数量，它等于上阶段和本阶段的空车剩余数量之和.

式(4)为空车提供站在某时间段内所滞留的空车量，它是由上阶段剩余的空车数量减去本阶段调配的空车数量得出，即在上阶段剩余的空车如果在本阶段内还没有被调配就认为这些空车在本阶段内出现了滞留.

式(5)为弧段能力约束，约束左侧表示在某时间阶段内通过弧段的车流量，此车流量需要小于等于该弧段在该时间阶段的最大通过能力.

式(6)为空车提供站的空车最大发送能力约束.

式(7)为空车需求站的空车最大接收能力约束.

式(8)为决策变量和中间变量的非负性质.

3 模拟退火算法求解

空车调整问题的本质为一个组合优化问题，本文采用模拟退火算法(Simulated Annealing，SA)进行求解.

求解过程分为两步.

第一步，在只考虑最短路的情况下，结合式(1)～式(4)、式(8)，利用模拟退火算法求解，然后考虑式(5)，找出所有不满足式(5)的弧段，再找到经过这些弧段的OD集合，调用K短路算法，将集合中的OD加入K短路作为邻域解.

1)初始解.

令所有的空车调整量初始解都为0.

2)邻域解.

3)冷却策略.

每次迭代温度控制采用下面的函数进行控制：

Tn+1=αTn， 0<α<1

(9)

式中Tn表示第n次迭代时的温度.

4)接受函数.

较差解可以接受的概率采用下式确定：

P(ΔZ,T)=exp(-ΔZ/T)

(10)

从公式可以看出较差解可以接受的概率是由当前循环设置的温度T和目标值的变差量ΔZ共同决定的.温度较高时，较差解被接受的概率较高；温度较低时，较差解被接受的概率较低.

5)终止条件.

当迭代时的温度下降到设定温度或迭代到一定的次数时目标函数还没有得到优化即算法终止.

4 算例分析

路网的拓扑结构如图2所示，路网中每条弧段都为双向弧段，弧段上的数字表示弧段的距离,单位为km.设空车在路网中的平均速度为50 km/h，假定路网中节点S1～S4为空车提供点，S6～S9为空车需求点.

表1和表2分别表示了空车需求点在不同的时间阶段对于不同车种的提供量和空车提供点在不同的时间阶段的空车需求量，本文中考虑了3种车种c1～c3.不同车种替代费用：c1与c2车种替代费用为5元；其他情况的替代费用较高，值为100元.

4.1 输入条件参数

目标函数中所涉及的费用参数：单位空车走行费用为50元/h；单位空车需求满足后，所产生的效益为2 000元；单位空车单个时间阶段的空车滞留费用为500元；单位空车单个时间阶段的空车未满足需求的费用为50元.每个时间阶段的时长为3 h.

模拟退火算法的参数:初始温度为500，终止温度为1，冷却比例为0.99，固定温度的迭代次数为10，次解的最大迭代次数为100，最大迭代次数为15 000.

4.2 计算结果

1)能力无约束.

在能力不受约束的情况下，通过模拟退火算法进行求解，各个弧段的能力利用情况如表3所示.

表1 空车提供点在不同时间阶段的空车提供量
Tab.1 Empty car supporting numbers of supporting stations in different time stages 辆

节点阶段1阶段2阶段3阶段4c1c2c3c1c2c3c1c2c3c1c2c3节点1200200400500200500600300100400500300节点2300200400100500300200500200500200100节点3200200400500600600300200400600600200节点4100200800800700400500600650600300200

表2 空车需求站在不同时间阶段的空车需求量
Tab.2 Empty car needing numbers of needing stations in different time stages 辆

节点阶段2阶段3阶段4阶段5c1c2c3c1c2c3c1c2c3c1c2c3节点6200300100400100200400500100500600100节点7400400500600600300500900300200100400节点8400500300700200400600700600300300400节点9300500600700700300200300200400500200

表3 能力不受限制情况下各弧段能力利用值

Tab.3 Capacity using values of all arcs without capacity constraints 辆

弧段能力利用弧段能力利用弧段能力利用弧段能力利用S5-S85234S6-S94314S2-S42212S4-S74351S1-S21126S1-S61498S3-S58324S5-S4 818S1-S31467S2-S32413S4-S54042S5-S66314

2)能力约束.

现将弧段S3-S5设为能力约束弧，最大能力约束为3 000辆；那么经过此弧段的所有OD集合，以及此OD集对应的K短路，如表4所示.

表4 能力限制情况下的受限制OD集合及K短路

将表4的备选径路加入对应的邻域集合，得出了在能力约束条件下的空车调整结果，此时路网的能力利用如表5所示，从表中可以看出限制弧段S3-S5能力利用值为3 000辆,达到最大.

表5 能力限制条件下各弧段能力利用值
Tab.5 Capacity using values of all arcs with capacity constraints 辆

由于篇幅限制，表6只列出了在阶段1时的结论，表示选择不同径路的空车调整结果.从表6中可以看出，分配结果只出现了车种c1和c2互相替换的情况，同时受能力约束影响的OD都选择了绕行的径路.

图3表示了模拟退火能力无约束、能力约束和能力约束且考虑了K短路3种不同情况下的迭代优化结果.从图中可以看出，3种情况都在迭代8 000次左右时达到了优化；第1种情况下调整的收益最大，第3种情况次之，第2种情况最少，因此,得出结论:在能力约束条件下采用K短路的方法比采用最短路的收益要高.

表6 阶段1时空车调整结果Tab.6 Empty car distribution results under stage one 辆

续表6

K短路节点节点6节点7节点8节点9c1c2c3c1c2c3c1c2c3c1c2c3第2短路节点1节点2节点3节点4c100000012100000c2000000600000c30000000050000c11122000001603700c23411000071110290c3002500000570044c1000144012401110c22706701120290c30033006700250054c1000000000000c2000000000000c3000000000000第3短路节点1节点2节点3节点4c10000005110000c2000000700000c30000000053000c100000030012110c2215000013001700c3001400000330028c127210101078016210c2140000010002200c300000530064000c1000000000000c2000000000000c3000000000000

5 结论

本文建立了在能力约束条件下的多车种空车动态调整优化模型，引入了空车服务网络，并采用融合K短路算法的模拟退火算法进行优化，设计了两步法优化策略，得到了较优解.研究了能力无约束采用最短路、能力约束采用最短路和能力约束且考虑了K短路3种不同情况下的迭代优化结果.结果表明在能力约束的条件下采用K短路的方法能得到相对较好的收益.该模型可以为路网中空车调整问题的研究提供一定的参考.然而，空车调整问题在实际生产中需要考虑的因素还很多，如车流运行时间受多种因素影响、列车车次接续和车站装卸车能力等都影响空车调配的效率，这些因素需要在下一步工作中继续研究.

[1] 果鹏文，林柏梁，余洋. 大规模路网上空车调配的区段中心优化[J]. 中国铁道科学，2001，22(2)：122-128. GUO Pengwen, LIN Boliang, YU Yang. The section center optimization method of empty car adjustment on large-scale railway network[J]. China Railway Science, 2001, 22(2):122-128.(in Chinese)

[2] 纪嘉伦，林柏梁，李福志，等. 用重心优化方法求解铁路网上空车调配问题[J]. 铁道学报，2001，23(3)：109-113. JI Jialun, LIN Boliang, LI Fuzhi, et al. Distribution of empty wagons on railway network by using the center-of-gravity-optimization method[J]. Journal of the China Railway Society, 2001, 23(3): 109-113. (in Chinese)

[3] 果鹏文，褚江，林柏梁. 用振荡法解大规模路网上的空车调配问题[J]. 中国铁道科学，2002，23(4)：111-117. GUO Pengwen, CHU Jiang, LIN Boliang. Reiterative adjusting method of empty wagon on large-scale railway network[J]. China Railway Science, 2002, 23(4):111-117. (in Chinese)

[4] 林柏梁，乔国会. 基于线路能力约束下的铁路空车调配迭代算法[J]. 中国铁道科学，2008，29(1)：93-96. LIN Boliang, QIAO Guohui. Iterative algorithm of railway network empty cars distribution based on restriction of route capacity[J]. China Railway Science, 2008, 29(1):93-96. (in Chinese)

[5] 温旭红,林柏梁,王龙,等.基于多商品网络流理论的铁路车流分配及径路优化模型[J].北京交通大学学报,2013,37(3):117-121. WEN Xuhong, LIN Boliang, WANG Long,et al. Optimization model for railway car flow assignment and routing plan based on multi-commodity network flow theory[J]. Journal of Beijing Jiaotong University, 2013,37(3):117-121. (in Chinese)

[6] 曹学明，林柏梁. 基于滞留费用的空车调配优化方法[J]. 铁道学报，2007，29(4)：18-22. CAO Xueming, LIN Boliang. An optimization method for distribution of empty cars based on stock cost[J]. Journal of the China Railway Society, 2007,29(4):18-22. (in Chinese)

[7] 程学庆，陆一新，尹传忠,等. 基于时间窗的铁路空车调配优化模型及求解[J]. 中国铁道科学，2007，28(6)：113-116. CHENG Xueqing, LU Yixin, YIN Chuanzhong, et al. Optimal model and solution of railway empty wagon distribution with time-window[J]. China Railway Science, 2007,28(6)：113-116. (in Chinese)

[8] 梁栋，林柏梁. 铁路空车调配的多阶段策略优化模型研究[J]. 铁道学报，2007，29(1)：1-6. LIANG Dong, LIN Boliang. Research on the multi-stage optimization model of empty railcar distribution[J]. Journal of the China Railway Society, 2007，29(1)：1-6. (in Chinese)

[9] 王龙，马建军，林柏梁，等.全路空车动态调配及路网分界口排空流量测算方法[J].铁道学报，2015，37(6)：1-9. WANG Long, MA Jianjun, LIN Boliang, et al. Dynamic empty car distribution for the whole rail system and calculation for empty car flow discharged over network boundaries[J]. Journal of the China Railway Society, 2015，37(6)：1-9. (in Chinese)

[10] LOXTON R, LIN Q, TEO K L. A stochastic fleet composition problem[J]. Computers & Operations Research, 2012,39 (12):3177-3184.

[11] YAGHINI M, KHANDAGHABADI Z. A hybrid metaheuristic algorithm for dynamic rail car fleet sizing problem[J]. Applied Mathematical Modelling，2013, 37(6):4127-4138.

Multi-type empty car dynamic distribution method based on capacity constraints

ZHANGHongbin1,2，DONGBaotian1，SUNYuanyun2

(1.School of Traffic and Transportation，Beijing Jiaotong University，Beijing 100044，China； 2.China Railway Information Technology Center，Beijing 100844， China)

Empty car service network of time and space is proposed to cater for the dynamic characteristic of railway transportation system, and the dynamic programming model based on capacity constraints is proposed considering the actual transport capacity constraints in the production. Empty car stranded costs and unsatisfied demand penalty costs related to time factor, car substitution costs are considered in object function. Railway network arc carrying capacity，empty car supporting and needing stations' capacity are all concluded in the restrain conditions of the formulation. A simulated annealing (SA) algorithm integrating K shortest path algorithm is designed, and a two steps optimization strategy is proposed to solve the problem. Finally, a simple network is to verify the model, and the results indicate that the integrating K shortest path algorithm can get preferable revenue under capacity constraints.

railway transportation; capacity constraints; multi-type empty car dynamic distribution; service network of time and space; simulated annealing algorithm

1673-0291(2016)06-0050-07

10.11860/j.issn.1673-0291.2016.06.009

2016-03-01

中国铁路总公司科技研究开发计划项目资助(2014X009-A，2016X006-D)

张红斌(1981—)，男，河南焦作人，博士.研究方向为铁路运输组织现代化.email:zhanghongbin2003@126.com.

U292.4

A