民勤荒漠沙枣树分形特征

马良清，杨福全，许丽

民勤荒漠沙枣树分形特征

马良清1，杨福全2，许丽3

（1.重庆市林业科学研究院，重庆 400036；2.甘肃省武威市林业技术服务中心，甘肃 武威 733000；3. 甘肃省武威市石羊河林业总场义粮滩分场，甘肃 民勤 733302）

以甘肃民勤荒漠成年沙枣树为研究对象，对不同径阶的标准木进行了全株破坏性取样。直接测量了树木的总生物量（含根、茎、枝、叶）、树冠形状、叶面积。并运用分形理论和方法，研究了叶片、树冠、整株树木的分形特征及其与生物学、生态学、环境、生长势的联系。结果表明：1）叶片周界分维数DLp均值=1.048。DLp与叶片圆度Rd呈反相关。叶片面积分维数DLa均值=1.337。DLa与叶片圆度Rd成正比。DLa反映了被调查的民勤沙枣的品种属性、栽培性质、生态学特性；2）树冠空间曲面分维数D(S-L)均值=2.304。树冠体积分维数D(V-L)均值=2.308。D(S-L)与树冠叶面积饱和值K2呈正相关。生长中庸的林木，D(S-L)≈2.2～2.3，与此相对应的K2≈0.6～0.7。D(S-L)与树冠垂直投影面的叶面积指数LAI值呈正相关。分维数D(S-L)平均值对应的LAI≈3。在一定范围内，D(S-L)随树木生长势的上升而增大，随立地条件的改善而增大。树冠分维数反映了树木的生长势和立地条件的优劣；3）整株树木分维数D(Wt-L)均值=2.410，D(Wt-L)的值映射出沙枣的中旱生植物、阳性植物、高光合植物特征。

沙枣；叶面积；树冠；生物量；分形

铅沙枣Elaeagnus angustifolia起源于中亚中心和近东——小亚细亚中心，广泛分布和种植在亚洲、欧洲、非洲北部、北美洲的一些干旱和半干旱地带。在我国，沙枣主要分布在西北各省区和内蒙古西部，零星分布于华北北部、东北西部，大致为34°N以北的地区[1]，是我国西北干旱荒漠和半干旱地区主要造林树种[2]。

树木及其生物构件，是一类不规则的、复杂奇异的几何形体。树木的生长以及它与环境的关系更是一类非线性行为。维度又是一个对象的基本属性。基于欧氏几何的经典测树学，系以研究规则图形为对象，很难描述树木及其生物构件的性状。

从20世纪70年代末到80年代初以来，逐渐形成了一门新兴学科——分形几何（fractal geometry）。20世纪90年代以来，随着研究的深入，形成了分形理论（fractal theory）。分形理论是一门新兴的非线性学科，它是研究自然界不规则和复杂现象的科学理论和方法[3]。

鉴于对沙枣的分形研究，目前尚未见报道。故该项研究旨在应用分形理论和方法研究沙枣的本质属性。其主要任务是，对沙枣进行全株破坏性取样，应用分形理论的方法，利用样本数据，计算沙枣树的叶片、树冠、整株树木的分形维数，从分形角度表达沙枣的本质属性，分析分维数同沙枣生物学特性、生态学特性、生长势之间的联系，为沙枣的培育和利用提供理论数据。

1 试验地概况与调查方法

1.1 试验地概况

研究区域系甘肃省民勤石羊河林业总场的沙井子分场和义粮滩分场。该区域东西北三面被腾格里沙漠和巴丹吉林沙漠包围。沙井子分场位于102°54′38.4″E、38°34′15.6″N；义粮滩分场位于103°22′43″E、38°38′29.6″N。海拔1 350 m左右。

年平均降水量113.0 mm，年平均气温8.8 ℃、年蒸发量2 675.6 mm[4]，年日照3 028 h[5]。土壤为荒漠化草甸土。地表覆沙，其厚度15～50 cm不等，其下有一薄层厚度不等的青灰色胶泥，质地粘壤。再其下是沙壤土。

1.2 调查方法和参数计算

1.2.1 调查方法

1.2.1.1 样木调查

选择生长正常、树冠完整、树木周围具有充足的采光空间、树冠未受其它林木欺压、树木未受人为和自然伤害的树木作为样木。样木的树龄在8～22年之间，胸径在2.5～41.4 cm之间，树高在2.4～11.4 m之间，每一个径阶选择2～3株，共选择样木41株，测量其胸径、树高、冠幅。测绘冠形图，伐倒样木，对每株样木进行全株破坏性取样，分别称量全株干、枝、根头、侧根的鲜生物量，并分别取样，在105 ℃下烘干至质量恒定，计算干、枝、根的烘干生物量。称量全株叶的鲜生物量，并取样，在85 ℃下烘干至质量恒定，绘制叶片图。使用Photoshop cs3测算每一叶片的面积La、圆度Rd、周长Lp、叶长Ll、叶宽Lw。分别计算各株样木的下列参数：鲜叶和烘干叶的比叶面积；树冠叶生物量和树冠叶面积LA；树冠空间曲面面积SA；树冠体积V；地上地下总生物量Wt。

1.2.1.2 样地调查

在1957～1975年用实生苗营造的林分中进行样地调查。每块样地的面积1 000 m2。记载样地位置、海拔、林地土壤、林下植物种类等因子；对活立木进行每木检尺。测量胸径、树高、最大冠幅等。

全部野外作业于1980年10月上旬和1981年9月4日～10月12日进行。这个时段，树叶已经成熟，整个树冠的叶面积达到最大值，树木根、干、枝、叶生物量和树木总生物量能代表测量当年的数值。

1.2.2 参数计算

1.2.2.1 叶片分维数计算

将叶片看作不规则图形（分形岛）。分形岛的分形边界长度和测量尺度密切相关。根据分形岛的面积与周长关系，确定叶片周长Lp、叶片面积La、周界分维数DLp之间的关系有：

式中：k1是尺度常数。根据(1)式有：

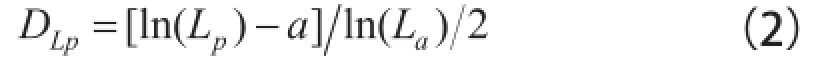
式中：a为待定常数。根据分形岛长度与面积的关系，推导的叶片面积分维数DLa有：

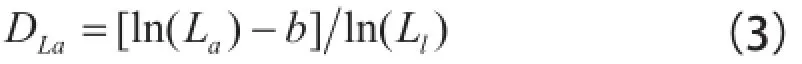
式中：Ll为叶片长宽尺度的最大值；b为待定常数[3]。

1.2.2.2 树冠分维数和整株树木的分维数计算

采用“双表面法”[6]，计算这两类分维数。当树冠放大或缩小的过程中，树冠叶面积（LA）同树冠空间曲面面积（SA）以及分维数D之间的关系可以表达为：

式中，c为待定常数。同理，树冠叶面积（LA）同树冠体积V以及分维数D之间的关系可以表达为：

式中，d为待定常数。根据式（4）和式（5）分别导出计算下列分维数的公式列于表1。即：基于树冠叶面积LA，计算树冠空间曲面的分维数D(S-L)；基于树冠叶面积LA，计算树冠体积V的分维数D(V-L)。鉴于整株树木是一个典型的支离破碎的形体，但它的总生物量Wt正比于它的体积，且总生物量与叶面积紧密相关，故利用单株树木地上地下总生物量Wt，计算基于树冠叶面积LA的整株树木分维数D(Wt-L)。

表1 分形计算公式汇总

2 结果和分析

2.1 叶片分形

叶片周界分维数DLp=1.048，叶片周长Lp与叶片面积La的相关系数R2=0.812（表2序号1）。而且DLp与La关系不显著（R2=0.000）（表2序号2）。说明沙枣叶片形状具有很好的自相似性，其形状是一类分形。DLp与叶片圆度Rd成反相关（图1）。

叶片面积分维数平均值DLa=1.337，叶面积La与叶片长宽尺度的最大值Ll的相关系数R2=0.733（表2序号3）。且DLa与叶片面积La大小关系不显著（R2=0.214）（表2序号4）。DLa与叶片圆度Rd成正比（图2）。

叶片周界分维数DLp反映了叶片周长Lp在平面的填充程度。叶片面积分维数DLa反映了叶片在以叶片长轴为边长的正方形中的填充程度。叶片周界分维数DLp和叶片面积分维数DLa所对应的叶片圆度值，可视为填充程度的量化值，其圆度值在0.41～0.67之间，平均值约0.57。

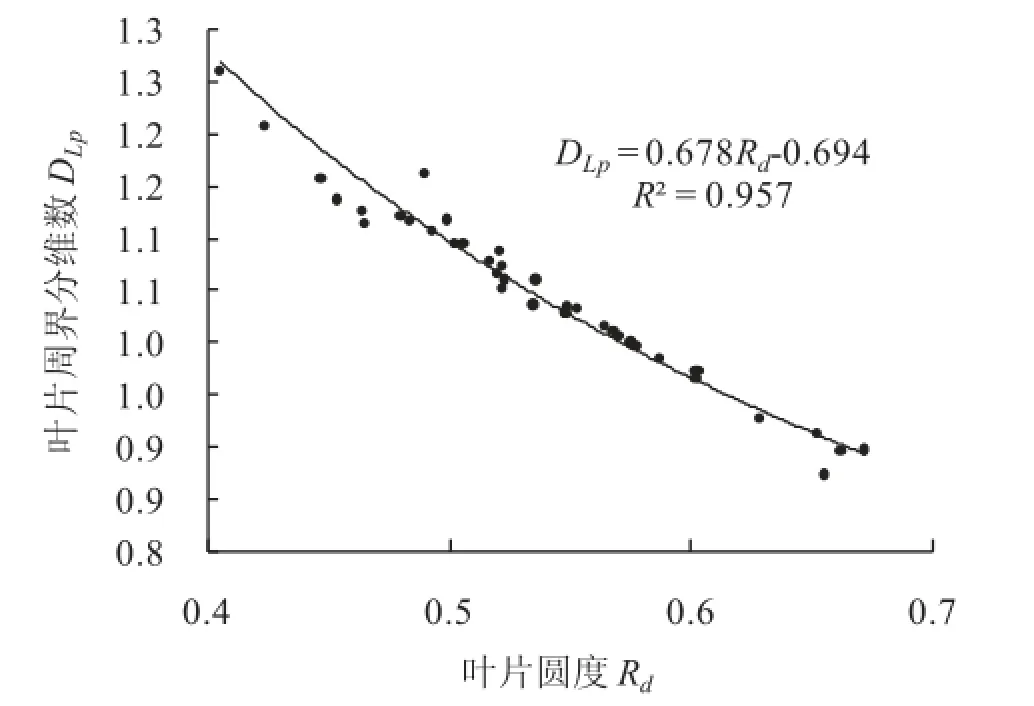
图1 叶片周界分维数随叶片圆度的变化

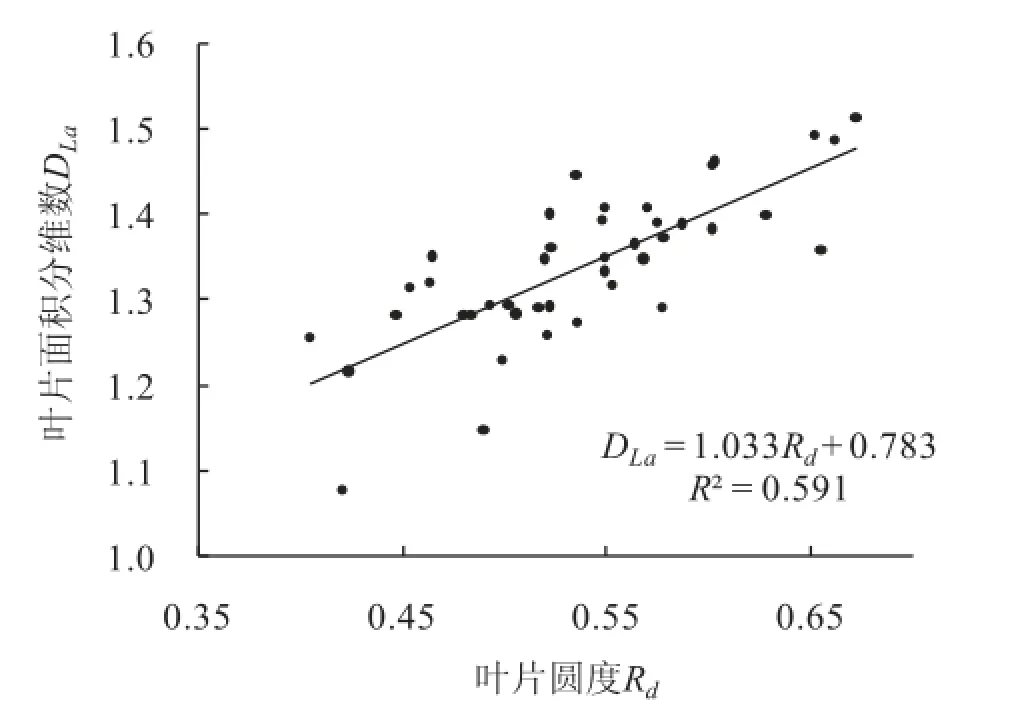
图2 叶片面积分维数随叶片圆度的变化

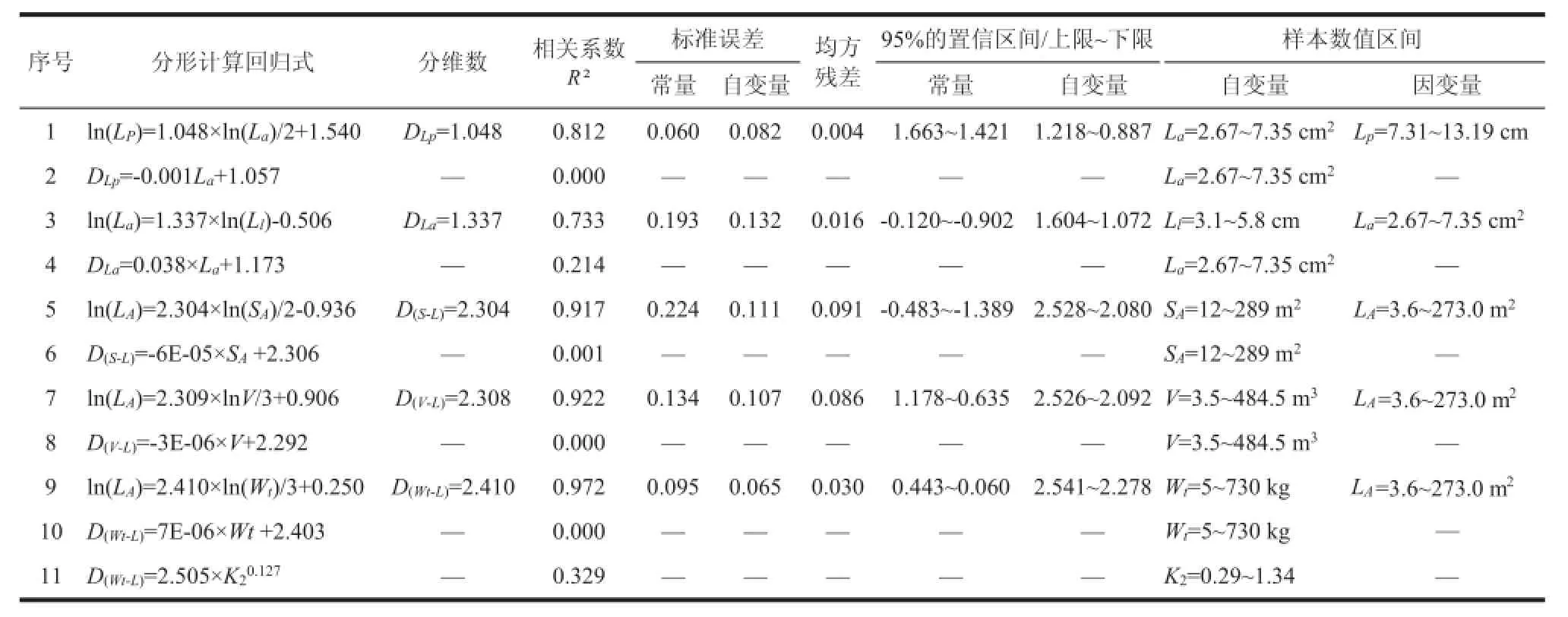
表2 单株沙枣树分形计算结果

2.2 树冠分形

鉴于树冠叶面积LA与树冠空间曲面面积SA以及与树冠体积V关系最密切。所以，通过两个途径对树冠进行分形计算：一是基于树冠叶面积LA的树冠空间曲面分形，树冠空间曲面是指树冠几何体的表面，这是一个封闭曲面；二是基于树冠叶面积的树冠体积分形。

基于树冠叶面积的树冠空间曲面的分维数平均值D(S-L)=2.304，树冠叶面积LA与树冠空间曲面面积SA的相关系数R2=0.917（表2序号5）。且树冠空间曲面分维数D(S-L)与树冠空间曲面面积大小无关（R2=0.001）（表2序号6）。

基于树冠叶面积LA的树冠体积V的分维数平均值D(V-L)=2.308，树冠叶面积LA与树冠体积V的相关系数R2=0.922（表2序号7）。树冠体积分维数D(V-L)与树冠体积的大小无关（R2=0.000）（表2序号8）。树冠体积分维数D(V-L)的数值与树冠空间曲面分维数D(S-L)的数值差别不显著。也反映出树冠空间曲面的大小影响着树冠叶面积的多少。表2中的序号5和序号7表明，树冠是一类分形。

从图3可见，树冠空间曲面分维数D(S-L)与树冠叶面积饱和值K2呈正相关。K2=树冠叶面积/树冠空间曲面面积。K2值反映了树冠叶片的丰茂程度。从野外样木调查和样地调查资料中注意到：生长衰弱的林木，树冠枝叶稀疏，树叶厚且单叶面积小，K2≤0.4，对应的D(S-L)≤2.1；生长中庸的林木，K2≈0.6～0.7，对应的D(S-L)≈2.2～2.3；生长强势的林木，K2≥1.0，对应的D(S-L)≈2.4～2.5。生长强势的林木，或生长在灌溉渠旁，或其林地的地下水位通常在2 m左右。

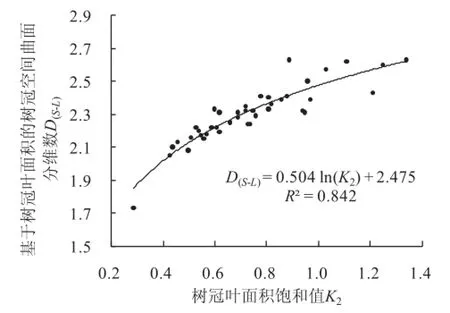
图3 树冠空间曲面分维数随树冠叶面积饱和值的变化

树冠垂直投影面的叶面积指数LAI，是指单株树木的叶面积与这株树木的树冠垂直投影面面积的比值。LAI值不仅反映了树叶在树冠的丰茂程度，而且还反映了树冠在垂直方向的占领程度。LAI值随胸径的增大而增大，因为树冠所占有的垂直空间随胸径的增大而增大。随立地条件的改善而增大，因为树冠叶的丰茂程度随立地条件的改善而增大。从图4可见，树冠空间曲面分维数D(S-L)与样木的LAI值呈正相关。样木的LAI值一般在2～5之间，对应的分维数D(S-L)在2.1～2.5之间。分维数D(S-L)平均值对应的LAI≈3。野外调查表明，这组样木，在造林初期地下水位约0.5 m，调查期间已经下降到2～3 m。所以，样木总的生长水平在中等偏下。这种情况与树冠平均分维数在2.304～2.308之间相吻合。

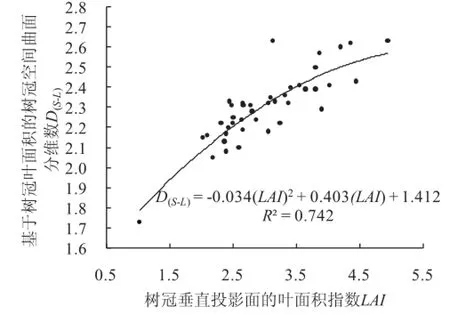
图4 树冠空间曲面分维数随树冠叶面积指数的变化

由上述分析可见，在一定范围内，分维数D(S-L)随树木生长势的上升而上升，随立地条件的改善而上升。树冠分维数不但反映了树冠叶片在树冠表面分布和树冠内部填充的密集程度。而且从一个角度反映了树木的生长势和立地条件的优劣。

2.3 整株树木分形

单株树木由根、茎、枝、叶等生物构件组成一个整体。这个整体占有的空间，形状奇异。它完全不同于欧氏几何所讨论的图形。鉴于质量正比于体积。所以，可以用树木地上地下的总生物量Wt代表这个奇异空间。还鉴于Wt与树冠叶面积LA是产品与生产者的关系。所以，Wt与LA关系最紧密（图5）。故使用树冠叶面积LA和总生物量Wt对单株树木奇异空间进行分形计算比较合适。

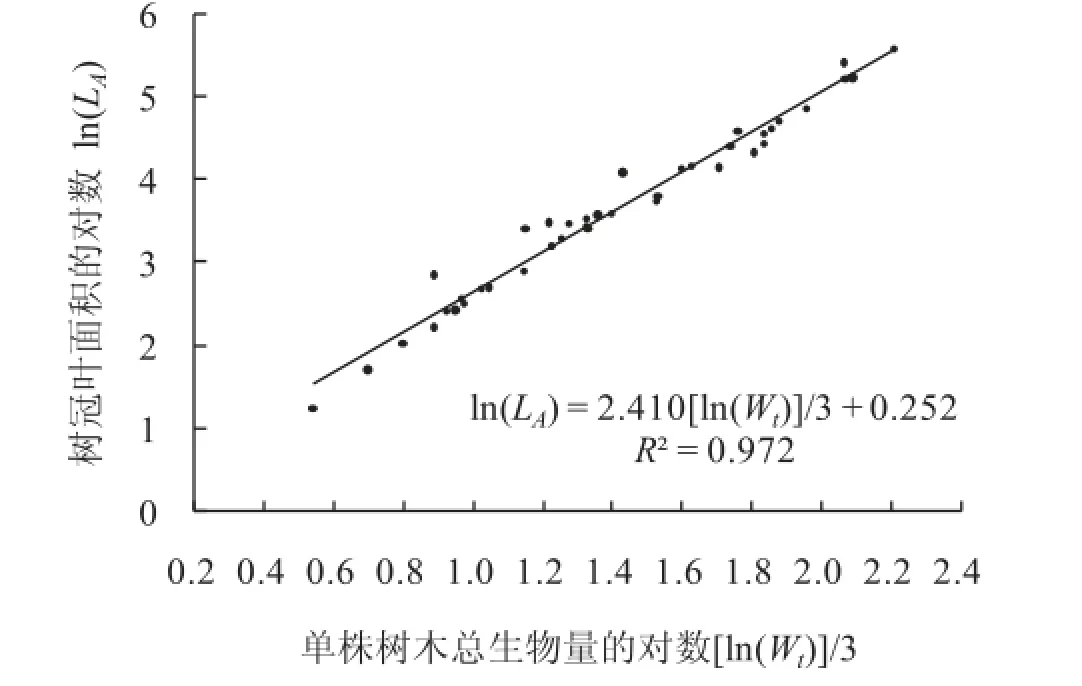
图5 树冠叶面积的对数随单株树木总生物量的对数的变化

基于树冠叶面积的总生物量分维数D(Wt-L)=2.410，树冠叶面积LA与单株树木地上地下总生物量Wt的相关系数R2=0.972（表2序号9）。且D(Wt-L)与总生物量Wt尺度大小无关（R2=0.000）（表2序号10）。可见，整株树木奇异空间也是一个分形。

从表2的序号11可见，分维数D(Wt-L)与树冠叶面积饱和值K2的相关系数R2=0.329，说明D(Wt-L)与树冠叶面积饱和值K2虽然有一定的关系，但与K2相关不紧密。K2值只是调查当年（并不代表过去若干年）树冠叶面积的丰茂程度。当年树叶的光合作用产物，需要扣除多年积累的有机质的呼吸消耗外，剩下的才用于积累。所以树冠叶面积的密集程度并不显著影响整株树木的分维数。

3 讨论和结论

3.1 讨论

该项目利用了大量的全株破坏性采样直接测量的样本数据进行研究。结果表明：应用分形理论去研究沙枣的形态特征、本质属性、生物质积累过程是可行的。应用分形理论的方法去研究沙枣叶片、树冠、全株树木的分形特征也是可行的。透过这些分形特征数据，不但映射出叶片的形态特征、叶片在树冠的分布特征等。而且还映射出沙枣的本质属性。例如：分类学属性、生物学属性、生态学属性等。特别是整株树木的分形特征，映射出生产者（叶片）同产品（生物质）之间的数量关系，或者说叶片生产生物质的能力。也在一定程度上反映了光能通过叶片转化为生物能的能力。应用分形理论对树木的研究结果，至少量化了物种的本质属性，在某种程度弥补了文字描述的冗长和繁琐。更重要的是，为认识、研究、保护、培育、利用这些物种提供了理论依据。

3.1.1 关于叶片分形

从分形几何角度看，沙枣叶片是一类分形。叶片的分形维数，只能大于1且小于2。其分维数反映了叶片对它所在的平面空间的填充程度，表征叶片的形状属性[3]。

在植物分类学中，通常可以注意到，对叶片形状有不同的文字描述。对于双子叶植物的叶片，一般有圆形、卵圆形等之类的描述。对于单子叶植物，因叶片狭长，一般描述为披针形等。这些描述，给人的数量感觉仅仅是，圆形和卵圆形叶片的长宽比（叶宽/叶长）较大，而披针形叶片的长宽比较小。仍然比较模糊。然而由式（3）可知，叶片面积分维数DLa同叶片长宽尺度的最大值的对数ln(Ll)成反比。即，叶片越狭长，Ll值越大，从而DLa值越小。叶片越接近圆形、卵圆形，DLa值越大。所以，一般来说，双子叶植物叶片的DLa值总是趋近于2，单子叶植物叶片的DLa值总是趋近于1。但是，这之间目前尚未有一个明确的数量界限。尽管如此，就一般趋势而言，双子叶植物叶片的DLa值大于单子叶植物。例如，双子叶植物叶片的分维数：桂花Osmanthus fragrans成熟叶片叶脉网络的平均分形维数为1.8[7]。胡杨Populus euphratica叶片叶脉的分形维数，柳叶形1.514，卵状菱形1.598，鸡爪形1.493[8]。田麻Corchoropsis tomentosa分形维数1.304，水花生Alternanthera philoxeroides分形维数1.464，荩草Arthraxon hispidus分形维数1.596，牵牛Pharbitis nil分形维数1.660。单子叶植物叶片的分维数：莎草Cyperus rotundus分形维数1.129，马唐Digitaria sanguinalis分形维数1.284[9]。沙枣属双子叶植物，该研究显示的沙枣叶片面积分维数（DLa=1.337）映射出双子叶植物叶片的特征。与沙枣的双子叶植物叶片形状属性相呼应。

被调查的沙枣，系栽培品种。其叶片的长宽比（叶宽/叶长=0.346）与栽培品种大果沙枣叶片接近（叶宽/叶长=0.328），但远大于自然野生种尖果沙枣叶片的长宽比（叶宽/叶长=0.265）。尖果沙枣的耐盐性也强于大果沙枣[10,11]。

可见，沙枣叶片的面积分维数从一个角度透射出被调查的沙枣的分类学属性、栽培属性。

在应用方面，还可以利用表2中序号3中的叶片面积分维数（DLa=1.337）和样本叶片的实测面积，计算出估计叶片面积La的回归式：

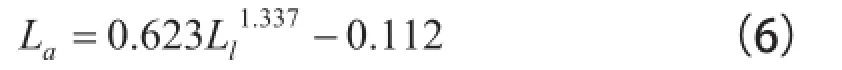
R2=0.765。式中，Ll为叶片长宽尺度的最大值。可以利用式（6）和叶片长宽尺度的最大值，估计出一组叶片的面积。但是，不宜利用这个回归式来估计一片叶的面积。因为叶片分维数受叶片圆度的影响。式（6）毕竟忽略了影响叶片面积的另一个变量（叶片长度或宽度）。过往有人写出过计算一类阔叶树叶面积La1的通用公式：

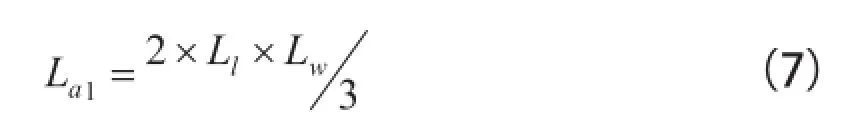
式中，La1为叶片面积；Ll为叶片长度。Lw为叶片宽度[12]。这个公式与叶片圆度无关。使用这个公式可以比较准确地计算出包括沙枣在内的一片或几片叶的面积。但这个公式毕竟是基于经验的结果，在当时这个公式的提出，并没有找到理论支撑。可见，叶片是一类分形的结论，也在一定意义上为写出计算叶片面积的广义公式提供了理论支撑。

3.1.2 关于树冠分形

如果一个立体空间的分维数大于2且小于3，那末它必定是一个分形。分维数的大小反映了这个分形对它所在的3维空间的填充程度。该研究结果显示，沙枣树冠空间曲面的分维数平均值D(S-L)=2.304，沙枣树冠体积的分维数D(V-L)=2.308。这样的分维数表明，沙枣叶片在树冠的填充程度属中等偏下。

过往的研究结果显示。第一，生长势强的树木的分维数大于生长势弱的树木。因为生长势强的树木，叶片在树冠中的填充程度大于生长弱势的林木。例如，成年针叶树树冠分维数，巨冷杉Abies grandis，生长势强者为2.42，生长中庸者为2.25[6]。美国黄松Pinus ponderosa，喜光。在遮光较多的林下生长不良[13]，生长势强者为2.57，生长中庸者为2.13。花旗松Pseudotsuga menziesii，喜光。生长势强者为2.52，中庸者为2.36。美国侧柏Thuja plicata，阴性，生长势强者为2.56，生长中庸者为2.41[6]。林带小钻杨树冠分维数为2.065～2.765[14]。20～50年的木榄树冠分形维数为2.21～2.54[15]。杨树无性系树冠的分维数，基于树冠叶面积的树冠表面分维数均值为2.405，基于树冠叶面积的树冠体积分维数均值为2.357[16]。第二，一般阳性树种的分维数小于阴性树。因为阳性树种的叶片忍耐遮阴的程度小于阴性树种。故叶片在树冠的填充程度小于阴性树种。例如：红豆杉属典型的阴性树种。东北红豆杉Taxus cuspidata，分形维数2.26～2.70，平均值2.45。希克斯红豆杉（Hicks Yew），是曼地亚红豆杉T. media的一个栽培变种，分形维数平均值2.42。东部白松Pinus strobes，性喜阳光充足的环境，稍耐荫，分形维数2.14～2.43，平均值2.24[17]。桦树树冠分维数2.20～2.26[18]。第三，叶子的分布状况不同，导致树冠分形维数不同。如果该树冠的叶子比较集中地分布在树冠表面，鉴于叶片的质量和面积正比于树冠的表面积。这种情况使树冠分形维数的值比较小。如果叶子均匀地分布于整个树冠之中，那么树冠分形维数则较大。

沙枣树冠的分维数较低（D(S-L)=2.304，D(V-L)=2.308），从分形角度映射出沙枣的以下特征。第一，树木的生长势。从图3和图4可见，树冠分维数比较大的树木，枝叶茂盛，生长旺盛，树叶在树冠的填充程度比较高。树冠分维数比较小的树木，枝叶稀疏，生长较弱。第二，阳性树种特征。沙枣本属阳性树种。

在林学实践中，估计树冠叶面积是一件很难的事。但为了给估计生物质产量和耗水量提供基础数据。常常又需要知道树冠的叶面积。过往曾有人报道过树冠叶面积与树冠空间曲面面积的关系，探索通过树冠空间曲面面积估计树冠叶面积的方法，且试图基于“约当引理”给予说明[19]，但这种调查毕竟是个案，文字描述也仅仅是定性的和有限的。分形理论的逐渐形成和分形方法的应用。为我们通过树冠空间曲面估计树冠叶面积提供了理论支撑和方法。于是，可以轻松地利用树冠的数字图像和树冠分维数估计树冠叶面积[17]。在这里，可利用沙枣树冠的空间曲面面积SA和沙枣树冠分维数（D(S-L)=2.304），估计出沙枣树冠叶面积LA。利用该研究结果有：

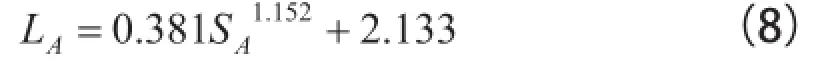
R2=0.918。这里似有必要赘述一句。根据分形理论，树冠的分形维数，只能大于2且小于3[3,6]。如果采用的公式或方法，例如盒计数法，估计出树冠的分维数，往往出现与实际情况不符的情况。说明盒计数法虽然用于估计面空间的分形特征可行，然而用于估计树冠立体空间的分形特征。尚有待完善。可见，“双表面法”[6]目前仍然是估计树冠分形特征的有效方法。

3.1.3 关于整株树木分形

整株树木是一个复杂奇异的立体空间。该研究以总生物量Wt代表整株树木。研究结果显示，总生物量的平均分维数D(Wt-L)=2.410。这表明，沙枣整株树木对它所在的3维空间的填充程度属中等稍偏下，沙枣树以较少的同化器官支撑着较多的生物量。这意味着沙枣的水分利用效率和光合效率比较高。

沙枣属于中旱生植物[20]。其水分利用率，仅次于典型的旱生植物沙拐枣Calligonum，高于旱生植物梭梭Haloxylon和喜湿的阳性树种杨树[21]。D(Wt-L)的值与水分利用效率相呼应。

沙枣属于高光合植物，净光合速率高于我国西北干旱荒漠地区的主要乔灌木树种，如：梭梭、二白杨Populus gansuensis[21-24]、多枝柽柳Tamarix ramosissima[25]，与沙拐枣相当[21]，还远高于沼泽地兴安落叶松Larix gmelinii[26]、黄山栾树Koelreuteria integrifolia[27]、热带雨林冠层树木[28]、华木莲Sinomanglietia glauca[29]。6～9月份的平均净光合速率，沙枣（(12.88±0.59) μmol/(m2·S)）低于胡杨（(15.3±0.30) μmol/(m2·S)）[30]。主要树种净光合速率的测定数据也从一个侧面证实了D(Wt-L)=2.410数值的客观性。D(Wt-L)的值与沙枣的光合效率相呼应。

由此可见，沙枣整株树木的分维数D(Wt-L)，从分形角度映射出沙枣的中旱生植物和阳性植物特征，映射出总生物量与叶面积的关系，映射出沙枣的高光合植物特征。从分形角度揭示出沙枣将太阳能转换为生物能的能量转换能力。以及即映射出该树种的生物学、生理学以及生态学特性。

过往研究分形理论在林业中的应用，多集中以树冠和叶片为对象。该项目研究全株树木的分形特征，是一种探索。鉴于质量正比于体积。故采用基于叶面积的全株树木总生物量的分形代替全株树木的分形有理论依据。且该研究结果表明，从分形几何学角度看，总生物量确实是在分数维的空间实现自己的增长。而且分形维数也与树种的本质属性相呼应。所以，该研究显示的单株树木总生物量分形特征也是符合实际的。该研究采用全株地上地下破坏性取样，虽然工作量大，但对于首次探索和奠定基础数据还是值得的。

与式（8）同理，还可以利用表2中序号9的回归式，根据树冠叶面积（LA）和总生物量分维数（D(Wt-L)=2.410），估计单株树木的总生物量。当然，这种建立在自相似性基础上的估计，仅存在于一定尺度范围之内[3]。

3.2 结论

以民勤荒漠成年沙枣树为研究对象，对不同径阶的标准木进行了全株破坏性取样。利用对树木根、茎、枝、叶的生物量和树冠形状以及叶面积的直接测量资料，运用分形理论和方法，对叶片、树冠、整株树木的分形特征及其与生物学、生态学、生长势、环境的联系进行了研究，结果表明：

民勤荒漠沙枣叶片周界分维数DLp均值=1.048。叶片周界分维数DLp与叶片圆度Rd成反相关。叶片面积分维数DLa均值=1.337。叶片面积分维数DLa与叶片圆度Rd成正比。叶片的面积分维数DLa从一个角度反映了被调查的民勤沙枣的生态学属性以及具有栽培性质的品种属性。

树冠空间曲面分维数D(S-L)均值=2.304。树冠体积分维数D(V-L)均值=2.308。树冠空间曲面分维数D(S-L)与树冠叶面积饱和值K2呈正相关。生长中庸的林木，D(S-L)≈2.2～2.3，与此相对应的K2≈0.6～0.7。D(S-L)与树冠垂直投影面的叶面积指数LAI值呈正相关。分维数D(S-L)平均值对应的LAI≈3。在一定范围内，分维数D(S-L)随树木生长势的上升而增大，随立地条件的改善而增大。树冠分维数不但反映了树冠叶片在树冠表面分布和树冠内部填充的密集程度。而且从一个角度反映了树木的生长势和立地条件的优劣。

整株树木分维数D(Wt-L)=2.410。这表明，沙枣整株树木对所在的3维空间的填充程度属中等偏下。且整株树木分维数D(Wt-L)映射出沙枣的中旱生植物、阳性植物、高光合植物的特征。

以上说明，沙枣的叶片分维数、树冠分维数、整株分维数，不仅是属于分形几何的形状参数，而且它也反映了沙枣的生物学和生态学内涵，反映了沙枣同环境之间的联系。同时也表明，分形理论和方法填补了经典测树学之不足。

致谢和致歉：该研究的野外调查工作，是作者在甘肃省林业勘察设计院工作期间，在院领导和同事的支持下完成的。崔昌杰、陈炳立、任志杰、朱耀芳等同志以及武威石羊河林业总场刘西波等同志参加了部分野外调查和内业计算。中国科学院沈阳应用生态研究所汪思龙研究员、陈楚莹研究员给予了热情指导。在此一并致谢！该文稿，于1982年动笔，因当年数学工具有限和工作变动，致使现在才提交正式文稿，特致歉！

[1] 于玮玮，阎国荣. 沙枣的资源及研究现状[J]. 天津农学院学报，2009，16（2）：46-50.

[2] 管文轲，徐娜. 沙枣资源利用研究与开发现状述评[J]. 安徽农学通报，2012，18（19）：119-120，213.

[3] 朱华，姬翠翠. 分形理论及其应用[M]. 北京，科学出版社，2011：1-23，50-53.

[4] 赵明瑞，刘明春，钱莉，王生元，李亚萍. 民勤绿洲1971-2010年沙尘暴特征及影响因素分析[J]. 沙漠与绿洲气象，2013，7（5）：35-39.

[5] 刘普幸. 近54年民勤绿洲气候变化趋势与周期特征[J].干旱区研究，2009，26（4）：471-476.

[6] BORIS ZEIDE PETER PFEIFER. A Method for Estimation of Fractal Dimension of Tree crowns [J]. Forestry Science, 1991, 37(5): 1253-1265.

[7] 刘庭凯，邹学新，赵婷婷，黄海波，王俊刚，麻琳. 桂花叶片的分形特征[J]. 武汉植物学研究，2005，23（2）：199-202.

[8] 张新明，彭俊. 胡杨叶片不同叶形的分形特征研究[J]. 防护林科技，2015（5）：55-57.

[9] 李志臣，姬长英. 基于图像分析的杂草分形维数计算[J].农业工程学报，2006，22（11）：175-178.

[10] 于玮玮，王小莉，李慧，阎国荣. 大果沙枣和尖果沙枣植物学特征比较研究[J]. 天津农学院学报， 2012，19（4)：36-38，50.

[11] 王泳，张晓勉，高智慧，刘伟，王沁. 盐胁迫对大果沙枣和尖果沙枣幼苗生长的影响[J]. 林业科技开发，2010，24（3）：25-28.

[12] 马良清. 一类阔叶树叶面积的通用公式测算法[J]. 生态学杂志，1990，9（1）：60-61.

[13] 樊军锋，周永学. 美国黄松介绍[J]. 陕西林业科技，1998（4）：70-73.

[14] 陈军，李春平，关文彬，张楠楠，汪西林. 林带小钻杨树冠的分维结构[J]. 林业科学，2006，42（12）：6-12.

[15] 梁士楚，王伯荪. 红树植物木榄种群植冠层结构的分形特征[J]. 海洋通报， 2002，21（5）：26-31.

[16] 李火根，黄敏仁，王明庥. 3种冠型分维数求算法在杨树无性系中的应用[J]. 南京林业大学学报（自然科学版），2005，29（6）：11-14.

[17] DONGSHENG ZHANG, ASHOK SAMAL, JAMES R BRANDLE. A Method for Estimating Fractal Dimension of Tree Crowns from Digital Images [J]. International Journal of Pattern Recognition and Artificial Intelligence. 2007, 21(3): 561-572.

[18] VOYTEKHOVSKY Y L. Are crowns of Betula pubescence Ehrh. fractal? [J]. Paleontological Journal, 2014, 48(12): 1315-1323.

[19] 马良清. 树冠的光合叶面积和光能利用潜力与树冠侧(表)面积的关系[J]. 生态学杂志，1986，5（6）：23-26.

[20] 黄俊华，买买提江，杨昌友，王朝锋. 沙枣（Elaeagnus angustifolia L.)研究现状与展望[J]. 中国野生植物资源，2005，24（3）：26-33.

[21] 龚吉蕊，赵爱芬，张新时. 多浆荒漠植物与中生植物对干旱胁迫反应的比较研究[J]. 北京师范大学学报（自然科学版)，2005，41（2）：194-198.

[22] 苏培玺，严巧娣. C4荒漠植物梭梭和沙拐枣在不同水分条件下的光合作用特征[J]. 生态学报，2006，26（1)：75-82.

[23] 井大炜，邢尚军，马海林，杜振宇，刘方春，马丙尧. 杨树光合特性及叶片营养分布的空间异质性[J]. 东北林业大学学报，2014，42（6）：34-37.

[24] 刘磊，庞洪影，杨峰，黄凤兰，孟凡娟. 3种引种杨树和3种乡土杨树苗叶的光合特性比较[J]. 西部林业科学，2010，39（3）：14-19.

[25] 张利刚，曾凡江，刘波，刘镇，安桂香，李海峰，袁娜. 绿洲—荒漠过渡带四种植物光合及生理特征的研究[J]. 草业学报，2012，21（1）：103-111.

[26] 王平，何春光，郎惠卿，周道玮.小兴安岭湿地植物的光合作用日变化研究[J]. 湿地科学，2003，l（2）：98-104.

[27] 童丽丽，王哲宇，吴世光，金静娟，许晓岗. 模拟淹水对黄山栾树幼苗的光合特性及部分抗氧化保护酶活性的影响[J]. 北方园艺，2014（1）：68-71.

[28] 赵俊福，谭正洪，宋清海，张一平，董丽媛，李愿旭. 热带雨林冠层树木和藤本之间光合作用特征参数比较[J]. 云南大学学报（自然科学版)，2012，34（1）：120-124.

[29] 郭起荣，俞志雄，施建敏. 华木莲与木莲属两树种光合生理生态研究[J]. 江西农业大学学报，2003，25（5）：645-651.

[30] 张毓涛，王文栋，李吉玫，李翔，徐金燕. 新疆乌拉泊库区沙枣与胡杨光合特性比较[J]. 西北植物学报，2011，31（2）：0377-0384.

Fractal Featureof Elaeagnus angustifolia Tree of in Minqin Desert

MA Liang-qing1, YANG Fu-quan2, XU Li3
(1.Chongqing Academy of Forestry, Chongqing 400036, China; 2.Gansu Province Wuwei City Forestry Comprehensive Service Center, Wuwei Gansu 733000, China; 3.Wuwei City Shiyang River Forestry Centre Yiliangtan Branch, Minqin Gansu 733300, China)

Based on the data from standard sample trees of different diameter grade in a mature Elaeagnus angustifolia plantation in Minqin desert, the fractal features of this species were examined. We measured the total biomass of trees (including roots, stems, branches and leaves), crown shape and leaf area, and analyzed the fractal features of leaf, crown and whole treeand their biological and ecological relationship with biology, ecology, growth potential and environment according to fractal theory and methodology. The results showed that1) leaf perimeter fractal dimension DLpmean value=1.048. DLpis inversely related to the leaf roundnessRd. Leaf area fractal dimension DLamean value=1.337. DLais proportional to the leaf roundness Rd. DLahas reflected the classification properties, cultivation nature and ecological characteristics of surveyed Elaeagnus angustifolia in Minqin desert; 2) Fractal dimension of crown spatial surface D(S-L)mean value =2.304. Fractal dimension of crown volume D(V-L)mean value=2.308. D(S-L)was positively correlated with the saturation value of the crown leaf area K2, For trees with moderate growth, D(S-L)≈2.2～2.3, and its corresponding K2≈0.6～0.7. D(S-L)is positively related with the leaf area index (LAI) of the vertical projection of the crown. Corresponding LAI of average value of fractal dimension D(S-L)≈3. Within a certain range, D(S-L)has increased with the growth vigor increment of trees or an improvement of site conditions. The crown fractal dimension has reflected the growth vigor and site conditions of trees; 3) Fractal dimension of the whole tree D(Wt-L)mean value=2.410, D(Wt-L)indicating that Elaeagnus angustifolia was mesophyte, xerophyte, light-demanding and high photosynthetic species.

Elaeagnus angustifolia; leaf area; tree crown; biomass; fractal.

S758.1

A

10.3969/j.issn. 1006-0960.2016.03.007

1006-0960（2016）03-0027-09

2016-08-08

马良清（1940—），男，四川射洪人，教授级高级工程师，长期从事森林培育与森林生态研究。发表论文20余篇。其中，生态学杂志3篇，林业科学1篇。E-mail: maliangqing@tom.com