基于FRFT的多分量对称三角LFMCW信号检测
2016-02-05纪秀美徐会法
张 莉,纪秀美,徐会法
(1. 中国人民解放军31008部队,北京 100091;2. 中国人民解放军31002部队,北京 100091)
基于FRFT的多分量对称三角LFMCW信号检测
张 莉1,纪秀美2,徐会法2
(1. 中国人民解放军31008部队,北京 100091;2. 中国人民解放军31002部队,北京 100091)
对称三角线性调频连续波(STLFMCW)信号是一种典型的低截获概率雷达信号。提出一种基于分数阶Fourier变换(FRFT)的聚类分析与“逐次消去”相结合的多分量STLFMCW信号检测方法。首先把多分量STLFMCW信号变换到FRFT域,利用聚类分析法实现对最强信号的检测,然后利用“逐次消去”法实现对其它信号的检测,直至检测到所有信号。最后,仿真验证了该方法的有效性。
对称三角线性调频连续波信号;信号检测;分数阶Fourier变换;聚类分析
0 引言
调频连续波(FMCW)雷达由于结构简单、体积小、距离分辨率高、无距离盲区、成本低、低功耗和低截获等优点,在军用导航、战场侦察与地面成像等领域得到越来越广泛的应用[1-3]。而对称三角线性调频连续波(STLFMCW)信号是FMCW雷达中常采用的信号形式[3]。在复杂电磁环境下,如何截获这类多分量低截获概率雷达信号已成为现代雷达侦察系统迫切需要解决的难题。
文献[4]利用Wigner-Hough变换提取STLFM-CW信号的特征参数,但是,当信噪比低于-6dB时已较难检测到信号。文献[5]提出一种基于Radon-Ambiguity变换和分数阶Fourier变换的ST-LFMCW信号检测与参数估计方法,在信噪比为-5 dB时,还可以得到很好的参数估计结果。文献[6] 利用FRFT适合处理LFM信号的特点,通过分析STLFMCW信号在分数阶Fourier变换(FRFT)域的分布特点,提出一种基于FRFT的对称三角LFMCW信号检测与参数估计方法,但是未考虑多分量对称STLFMCW信号的检测。
本文力图在FRFT域实现多分量STLFMCW信号在低信噪比条件下的检测。提出一种聚类分析与“逐次消去”相结合的检测方法,首先把在多分量STLFMCW信号变换到FRFT域,利用聚类分析实现对最强信号的检测,然后采用“逐次消去”法实现对其它信号的检测,直至检测到所有信号。
1 分数阶Fourier变换
信号x(t)的FRFT定义式为:
式中FRFT的变换核Kp(t,u)为:
(2)
式中,Aα=(1-jcotα)1/2,α=pπ/2为FRFT的旋转角度,p为FRFT的阶数,可以为任意实数。Xp(u)的逆变换为:
(3)
由式(3)可以看出,信号x(t)由一组权系数为Xp(u)的正交基函数K-p(t,u)所表征,基函数为LFM的复指数函数。
2 STLFMCW信号的模型
STLFMCW信号的每个周期包括正、负调频率的两部分LFM信号,其表达式分别为[7]:
(4)
式中,A为幅度,fc为载频,ΔF为调制带宽,T=2tm为调制周期。信号的正、负调频率分别为μ=ΔF/tm和-μ=-ΔF/tm。两个周期的STLFMCW信号的时频分布图如图1所示[6]。
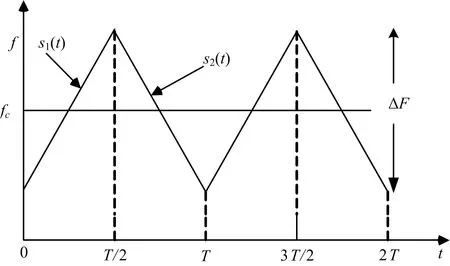
图1 两个周期的STLFMCW信号的时频分布图
假设雷达侦察接收机实际接收到的多分量STLFMCW信号模型为:
(5)
式中,s(t)由式(4)决定,K为信号分量的个数,w(t)为高斯白噪声。
3 STLFMCW信号的FRFT
由于FRFT可以理解为角为α的时频面旋转,根据该性质,分析STLFMCW信号在FRFT域的频谱分布特征。关于FRFT的数值计算,本文采用文献[8~9]提出的计算方法,信号的量纲归一化采用文献[10]提出的离散尺度变换法。设信号的观察时间为Td,则信号的时域区间为[-Td/2,Td/2]。两个调制周期的STLFMCW信号的时频分布及其在FRFT域的投影如图2所示。α01、α02、α03和α04分别为STLFMCW信号包含的四段LFM信号的“最佳”分数阶旋转角,在其对应的FRFT域内,STLFMCW信号呈现能量尖峰。umax01、umax02、umax03和umax04分别为四段LFM信号的尖峰的u坐标值。该两个调制周期的STLFMCW信号在(u,α)平面上的四个尖峰的坐标存在如下关系:
f01、f02、f03和f04分别为STLFMCW信号包含的四段LFM信号在f轴上的截距,也是利用FRFT得到的信号的初始频率[5],并且f01=f04,f02=f03。
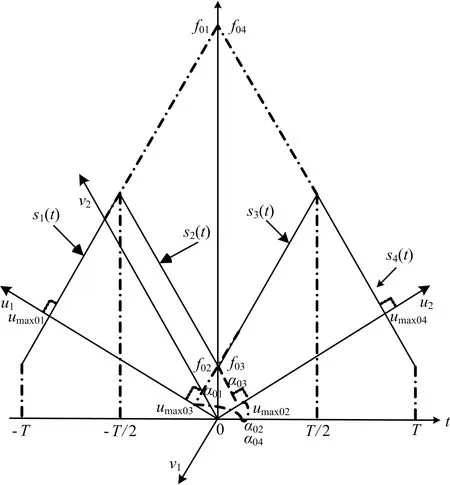
图2 两个周期的STLFMCW信号的时频分布在FRFT域上的投影
经上述分析可知,STLFMCW信号的每段LFM信号在其“最佳”分数阶域内都会呈现出能量尖峰,并且各个尖峰的高度相同;正调频率部分s1(t)与s3(t)的“最佳”分数阶旋转角相同,即它们的尖峰在平面(u,α)上的α轴坐标相同,它们在u轴上的距离为:
(11)
负调频率部分s2(t)与s4(t)也具有相同的性质;s1(t)与s4(t)对应的尖峰在平面(u,α)上的u轴坐标相同,并且两个尖峰在α轴上各自到α=π/2的距离相等,s2(t)与s3(t)之间也具有相同的性质。这些特征可以作为检测和识别STLFMCW信号的依据。
由图2可知,STLFMCW信号在各个FRFT域的频谱幅度为其包含的各段LFM信号在u轴上的频谱幅度叠加值,并且,STLFMCW信号的各段LFM信号的频谱在f轴上完全重叠。这会导致STLFMCW信号在频域或靠近频域的FRFT域的频谱叠加幅度大于或接近于其“最佳”分数阶旋转角α01和α02时的信号尖峰的高度,尤其是在低信噪比条件下,观测信号包含的周期数较多,以及信号的带宽较小时,这种现象更易发生。显然,这个问题增加了FRFT对多分量STLFMCW信号的检测能力。
4 多分量STLFMCW信号的检测
对于STLFMCW信号的检测与参数估计,包括其包含的多段LFM信号的检测与参数估计。由文献[11]可知,各段LFM信号由FRFT得到的参数估计表达式为:

(14)
由式(11)可得:
(15)
信号的调制周期与载频分别:
上述式中的符号含义与图2中的符号相同。式(14)~(17)也表明利用FRFT检测STLFMCW信号时,观察信号必须至少包含两个正调频率部分或负调频率部分,否则,无法估计STLFMCW信号的调制带宽。
本文采用聚类分析与“逐次消去”相结合的方法实现对多分量STLFMCW信号的检测。引入了基于广度优先搜索邻居(BFSN)的聚类算法[12],对STLFMCW信号在(u,α)平面上的多个尖峰进行聚类分析,然后,剔除由信号频谱叠加造成的奇异类,实现STFMCW信号的正确检测[6]。
4.1 平面切割
本文采用基于最大值的平面切割法,处理过程如下[6]:

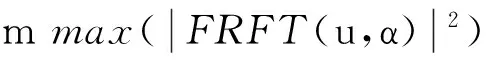
X=(x|x(zij,u,α),zij>mmax(Z))
(18)
4.2 信号尖峰的聚类
信号尖峰的聚类过程为[6]:
步骤1:求出聚类分析输入集X。
步骤2:求相异度矩阵。设聚类分析输入集X的对象数量为n,xi和xj(1≤i,j≤n)为其中的任意两个对象,它们在(u,α)平面上的坐标分别为(ui,αi)和(uj,αj)。定义d(xi,xj)为对象xi和xj之间近似性的量化表示。因为对象xi和xj在(u,α)平面上为两个点,其近似性由两点之间的距离大小决定,所以用欧几里德距离估算d(xi,xj)。n个对象两两之间的近似性的表现形式为一个n×n维的矩阵,该矩阵为对角元素是1的对称矩阵,称其为相异度矩阵。
步骤3:从输入集X中某任意对象出发,基于广度优先和距离参数r,依次搜索该对象的直接邻居和间接邻居。具体实现,本文使用队列算法,即找出队首元素的所有邻居,把它们从队尾压入,然后将队首弹出。该算法实现方便。
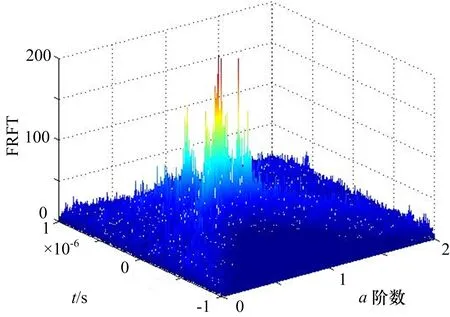
其中,直接邻居和间接邻居的概念分别为:1)直接邻居,给定对象b及距离参数r,对于任意对象x,若d(b,x)≤r,则称x为b的直接邻居,对象b所有直接邻居的集合称为b的全部直接邻居,记为Db;2)间接邻居,设n个对象x1,x2,…,xn-1,xn满足xn仅是xn-1的邻居,x1仅是x2的邻居,xk是xk-1和xk+1(1 步骤4:判断所有找到的直接邻居和间接邻居是否满足设定的类门限参数λ,如果满足,则将它们合并,从而完成一类聚类。 步骤5:重复步骤3和4,完成所有对象的聚类。 其中,距离参数r用于控制聚类时类和类之间的距离,参数λ可以用来控制聚类的形状。 4.3 信号检测的实现步骤 步骤2:用式(18)对Z进行平面切割,获得BFSN聚类算法的输入集: 步骤3:利用BFSN聚类算法对输入集进行聚类分析,得到聚类结果。 步骤4:对聚类结果进行排序,按照各个类对应的信号尖峰的高度由大到小的顺序进行排序。 步骤5:依据STLFMCW信号尖峰的分布特点,将同一个STLFMCW信号包含的类进行组合,组合过程如下: 组合依据: STLFMCW信号包含的调频率相同的LFM信号的尖峰在参数(u,α)平面上具有相同的α坐标,并且,调频率相反的LFM信号的尖峰在轴α=π/2的两侧,并且它们各自到α=π/2的距离相等。 组合方法:对经过步骤4排序后的类,采用穷举的方法,从第一个类开始,逐个类进行比较,寻找满足如下关系的所有类,并把它们分为一组,作为一个STLFMCW信号:1)如果几个类的α坐标相同、不等于π/2,(即|α-π/2|≥σ,σ为一个限制条件,本文选取σ=0.05,雷达侦察接收机可以根据担负的任务合理选择一个值),而且,它们还有关于α=π/2对称的其它类,并将它们一起组合为一组,即一个STLFMCW信号,然后,将上面已选择的类排除;2)采用上述方法再对剩余的类进行组合,直至组合完所有满足上述条件的类。 步骤6:选择每组中的具有相同α坐标的两个类,并求这两个类各自包含元素的α坐标的平均值,以这两个平均值作为信号的两个尖峰的坐标α01与α02。 步骤8:将得到的参数估计值分别代入式(13)~(17),获得STLFMCW信号的各个参数的估计值。 步骤9:采用“逐次消去法”消去已检测的信号的所有尖峰,将信号变换的时域,再对信号分别求旋转角α∈[0,π]的FRFT,得Z1=|FRFT(u,α)|2,搜索Z1=|FRFT(u,α)|2的最大值,如果max(Z1)≥Th,则说明还有剩余信号,按照上述方法,重复对信号进行检测与参数估计,直至剩余信号的幅度小于给定的门限。 由图4可以看出,多分量STLFMCW信号的频谱在频域内叠加,导致叠加的频谱幅度高于信号在其“最佳”分数阶Fourier域内的尖锋,给信号检测与参数估计带来更大的困难。通过采用聚类分析可以很好地解决这个问题。 图3 两个STLFMCW信号FRFT模值平方的三维图 图4 两个STLFMCW信号的聚类分析结果图 由于多分量STLFMCW信号的频谱叠加更为严重,本文利用STLFMCW信号在FRFT域的频谱分布特征,以及FRFT适合处理多分量LFM信号的优点,提出基于FRFT的聚类分析与“逐次消去”相结合的多分量STLFMCW信号检测方法,较好地实现了对多分量STLFMCW信号的检测。该方法利用STLFMCW信号的分数阶频谱分布特征,把聚类分析算法的数据挖掘能力应用于信号检测,扩展了信号检测方法,具有一定的理论价值和实用价值。■ [1] 杨勇, 谭渊, 张晓发, 等.LFMCW雷达运动目标距离与速度超分辨估计[J].信号处理, 2010,26 (4):626-630. [2] 吴礼, 彭树生, 肖泽龙, 等.对称三角线性调频连续波雷达信号多周期模糊函数分析[J].南京理工大学学报(自然科学版), 2009,33(1):74-78. [3] 梁毅, 王虹现, 刑孟道, 等. 调频连续波SAR信号分析与成像研究[J].电子与信息学报, 2008,30 (5):1017-1021. [4] Liu Feng, Xu Huifa, Sun Dapeng, et al. Feature extraction of symmetrical triangular LFMCW signal using Wigner-Hough transform[J]. Journal of Beijing Institute of Technology, 2009, 18(4): 478-483. [5] 袁伟明, 王敏, 吴顺君.对称三角线性调频连续波信号的检测与参数估计[J].电波科学学报, 2005,20(5):594-597. [6] 刘锋, 徐会法, 陶然.基于FRFT的对称三角LFMCW信号检测与参数估计[J].电子与信息学报, 2011,33(8):1864-1870. [7] Phillip EP. Detection and classifying low probability of intercept radarsecond edition[M]. 2nd ed. Boston, Artech House, 2009:81-119, 405-547. [8] Ozaktas HM,Arikan O,Kutay MA, et al. Digital Computation of the fractional Fourier transform[J]. IEEE Transactions on Signal Processing, 1996,44(9):2141- 2150. [9] Bultheel A, Héctor E, Sulbaran M. Computation of the fractional Fourier transform[J]. Applied and Computational Harmonic Analysis, 2004,16(3): 182- 202. [10]赵兴浩, 邓兵, 陶然.分数阶傅里叶变换数值计算中的量纲归一化[J].北京理工大学学报, 2005,25(4): 360-364. [11]Qi Lin, Tao Ran, Zhou Siyong, et al. Detection and parameter estimation of multicomponent LFM signal based on the fractional Fourier transform[J]. Science in China(Ser.F, Information Science), 2004,47(2):184-198. [12]钱江波, 董逸生.一种基于广度优先搜索邻居的聚类算法[J].东南大学学报(自然科学版), 2004,34(1): 109- 112. Detection of multicomponent symmetrical triangular LFMCW signal based on fractional Fourier transform Zhang Li1, Ji Xiumei2, Xu Huifa2 The symmetrical triangular linear frequency modulated continuous wave (STLFMCW) signal is a sort of typical low probability of intercept (LPI) radar signal. A novel method is presented to detect multicomponent STLFMCW signal based on the FRFT, clustering analysis and “elimination one by one”. First, the multicomponent STLFMCW signal is transformed to fractional Fourier domain. The strongest signal is detected by clustering analysis method. Secondly, the other signal is detected by “elimination one by one” method. Finally, simulations verify the effectiveness of the method. STLFMCW signal;signal detection;FRFT;clustering analysis 2016-09-08;2016-11-02修回。 张莉(1972-),女,工程师,主要研究方向为数据分析理论及应用。 TN971; TN974 A
5 仿真验证
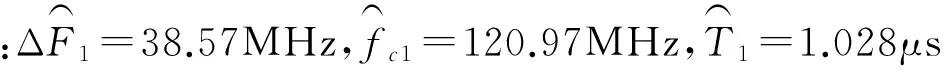

6 结束语
(1.Unit 31008 of PLA,Beijing 100091,China;2.Unit 31002 of PLA,Beijing 100091,China)
