煤矿井下人员安全疏散建模与仿真

王宛平，　李世豪

(1.河南质量工程职业学院 信息工程系， 河南 平顶山　467000；

2.平顶山工业职业技术学院 计算机与软件工程学院， 河南 平顶山　467001)



煤矿井下人员安全疏散建模与仿真

王宛平1，李世豪2

(1.河南质量工程职业学院 信息工程系， 河南 平顶山467000；

2.平顶山工业职业技术学院 计算机与软件工程学院， 河南 平顶山467001)

摘要：针对煤矿井下出现安全事故时人员的安全疏散问题，建立了煤矿井下人员安全疏散模型。该模型中井下巷道被划分为网格，通过设置“成员流势”来反映网格距离疏散出口的位置，从而确定疏散人员移动方向和路径，同时结合疏散成员移动速度、成员响应时间、灾害检测时间获得疏散时间。仿真结果表明，该模型能直观呈现人员疏散动态过程，为制定安全疏散方案提供数据参考。

关键词：井下疏散； 疏散模型； 成员流势； 疏散路径； 疏散时间

0引言

煤矿生产是一种安全事故频发的高风险作业，当灾难发生时，有效的疏散通道和应急设施是确保矿工安全的重要保障。然而煤矿井下巷道布局复杂，无法开展大规模的疏散演练。参考文献[1]以避难硐室为基础，建立了以时间为主要参数的人员疏散模型，得出了评价人员逃生效率的安全疏散系数；参考文献[2]对煤矿井下人员疏散进行了计算机仿真模拟，验证了采用人员疏散模拟技术对矿井人员流动和疏散行为进行研究的可行性。为了评估井下人员安全疏散流程和应急设施布局的合理性，本文建立了煤矿井下人员安全疏散模型，并利用计算机模拟的疏散场景进行仿真，可为井下人员疏散提供有效参考。

1模型构建

人员疏散的最基本特征是一种群体性的灾害逃生行为。由于环境、人员响应初始位置和个体行为都存在差异，建立煤矿井下人员安全疏散模型时，将群体划分为个体并研究疏散过程中的个体行为。采用拉格朗日法描述个体即成员的运动轨迹。

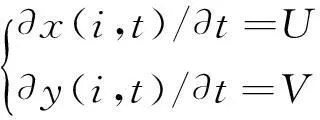
(1)

式中：x(i,t),y(i,t)分别为t时刻成员i在x和y方向的位置，i=1，2，…，n(n为疏散成员数量)；U，V分别为t时刻成员i在x和y方向的速度。

1.1网格设置

设置网格大小时考虑每个成员肩宽及成员之间适当的间隙，将巷道分成0.5 m×0.5 m网格，每个网格表示巷道的位置，网格可以为空，也可以被矿工或障碍物占用。

1.2成员移动方向

物理学中正电荷总是从高电位流向低电位。鉴此，本文提出用“成员流势”代表疏散时成员与出口的距离。规定出口处网格的“成员流势”为0，与其相邻网格的“成员流势”递增1；若网格被障碍物占用，则“成员流势”设定为最大值1 000 000。依据此规定，网格的“成员流势”不断增加，可获得煤矿井下不同位置的“成员流势”分布情况如图1所示(阴影区域表示障碍物占用的空间)。

图1　“成员流势”分布

成员可以在4个相邻网格间自由移动，但在疏散时任何成员的有效移动方向由“成员流势”和网格实际占用的可能性确定。疏散模型中的成员总是向未被占用且满足一定概率的低“成员流势”的网格移动。成员在方向j(j=1，2，3，4分别表示前、后、左、右4个方向)上移动的概率为

(2)

式中：Bmin用于确定任何4个相邻网格是否存在“成员流势”最低的网格，若存在Bmin=1，若不存在Bmin=0；Oj用于确定任何4个相邻网格是否被占用，若占用Oj=0，若未占用Oj=1。

成员疏散过程中从其当前位置开始，每一步都选择其相邻的低“成员流势”的网格作为移动的目标网格[3]，直至到达安全出口，这样该成员的疏散路径才最短、最省时、最安全。

1.3成员移动速度

成员移动速度是疏散模型的一个重要参数，不同人群密度的成员移动速度不同。日本学者Togawa开发了基于网格矩阵分析的成员移动速度和人群密度的模拟系统[4]，成员移动速度为

(3)

式中：v0为成员正常步行速度；ρ为人群密度。

当人群密度减小时成员移动速度会增加，但实际上成员移动速度不会无限制地增加，当其达到一定程度时将保持一个最大值。考虑到在灾难和特殊地理条件下的人员响应，成员移动速度最大值设定为1.5 m/s(可根据实际情况重新设置)，成员正常步行速度设定为1.3 m/s。

1.4疏散时间

当危险情况发生时周围环境会对人的行为产生影响。因此，对成员行为变化的推测，要在响应时间方面进行必要的调整[5]。将响应时间引入疏散模型中，则成员i的疏散时间为

(4)

式中：tp为灾害检测时间；ta(i)为成员i响应时间；trs(i)为成员i疏散到安全区域所需的时间。

其中

(5)

式中：int表示取整数；tmax，tmin分别为最大和最小响应时间；R为0～1的随机数。

疏散人群中某一成员从当前所处位置移动到安全出口处所需的疏散时间计算流程如图2所示。人群疏散时一个很重要的参数是最后一个成员疏散到安全区域的时间，其决定了总的疏散时间。

2仿真实验

2.1仿真条件

某煤矿井下工作面示意如图3所示。其中采煤工作面长100 m、宽2 m；轨道运输巷宽4 m，被障碍物(如电缆、发电机、通风机、水泵等设备)占据的轨道运输巷允许疏散矿工通过的最大宽度为1 m；主巷道宽6 m；与主巷道相连的避难硐室面积为10 m×4 m=40 m2，且只有1个进入避难硐室的出口。由于灾难发生时回风巷可能充满污浊的空气，矿工疏散时通过由实线箭头和虚线箭头指示的2条路径自由选择进入避难硐室。

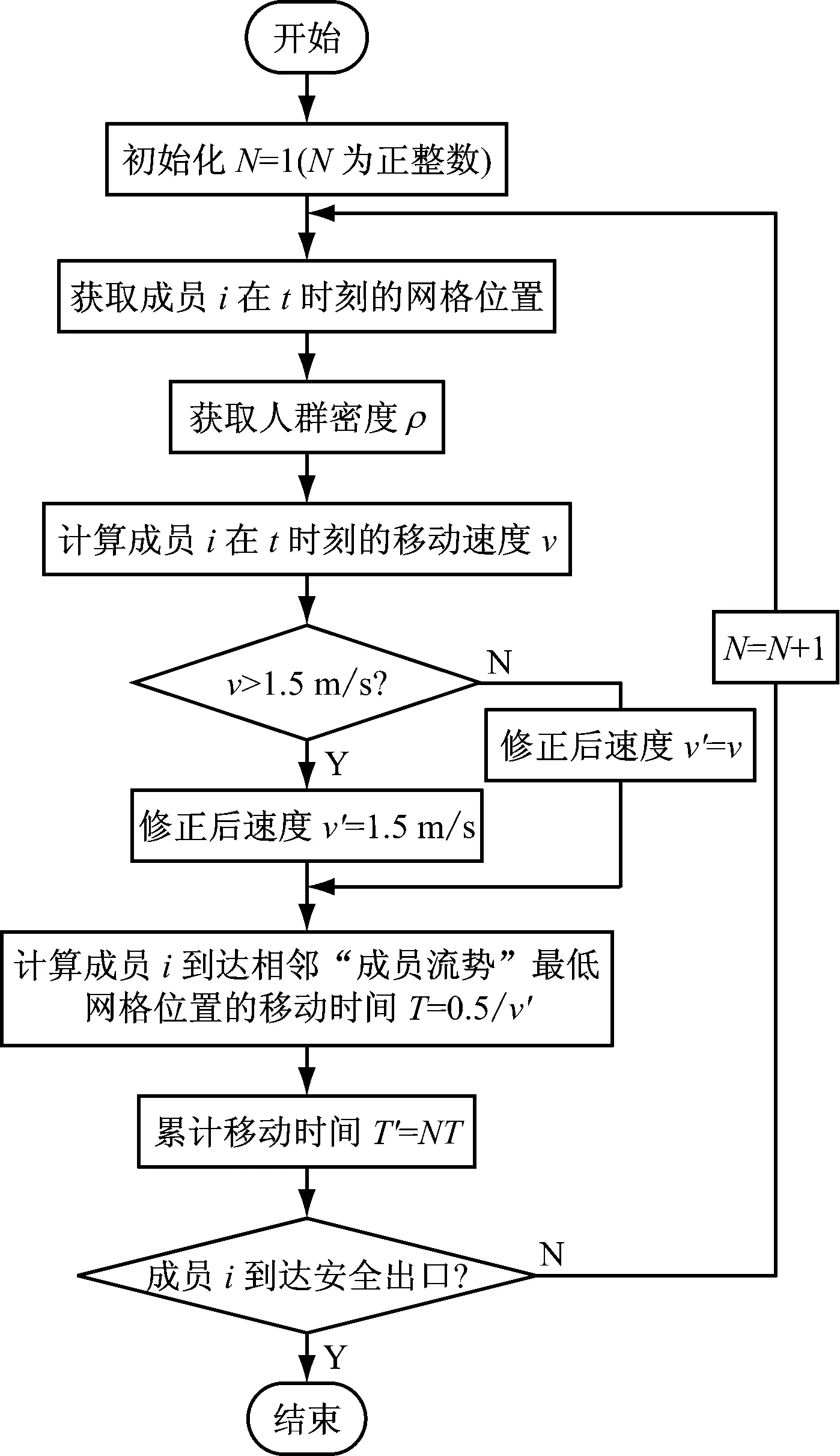
图2　单个成员疏散时间计算流程

考虑到煤矿井下的实际情况，将采煤工作面及附近区域的所有矿工添加到疏散成员组。假设有身体状况相同或相近的40个矿工在采煤工作面、10个矿工在主巷道和轨道运输巷，通过式(6)获取成员的坐标。仿真时设定灾害检测时间为10 s，最大响应时间为20 s，最小响应时间为5 s，当最后一个矿工疏散到安全区域后整个安全疏散过程结束。

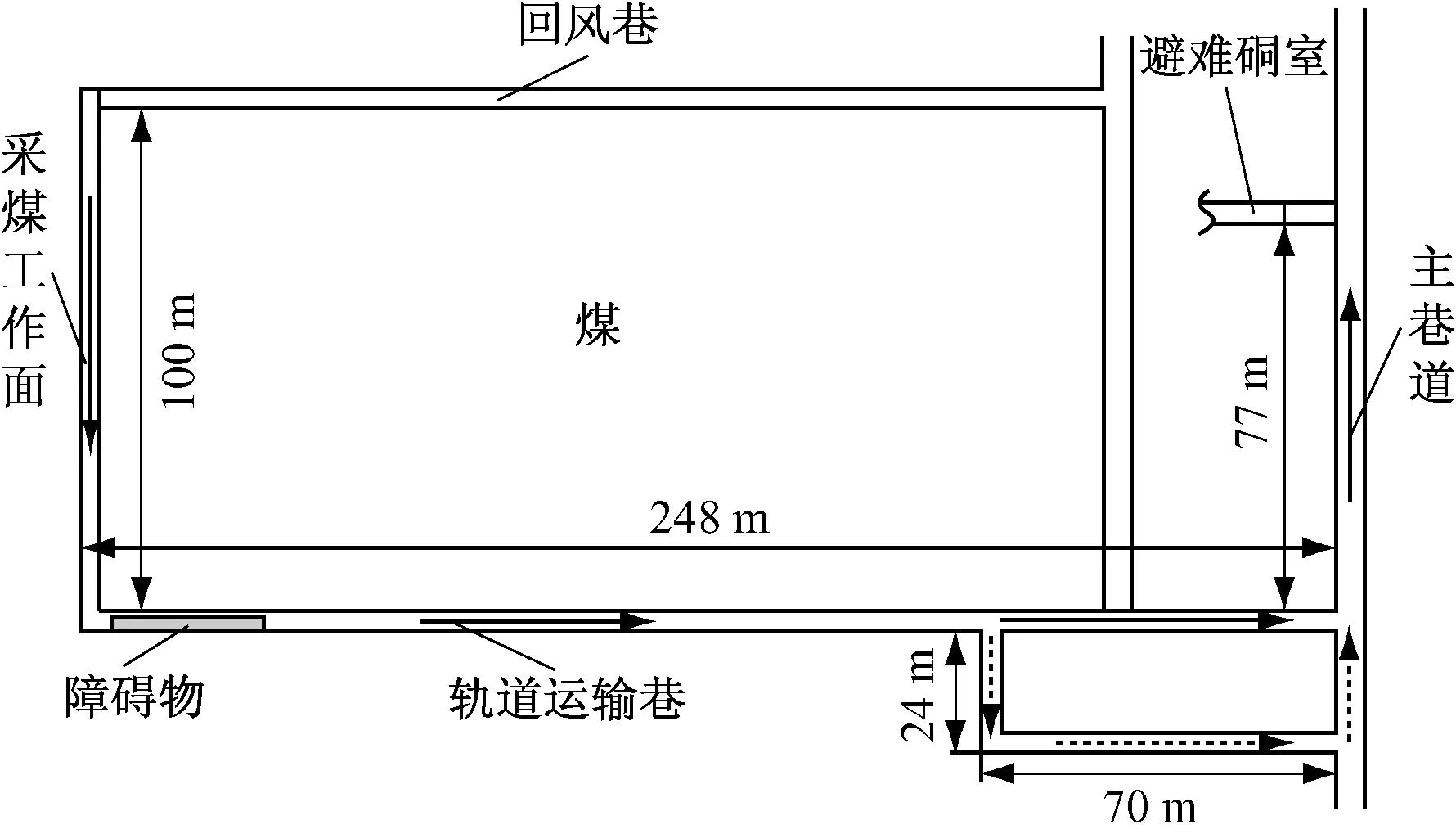
图3　某煤矿井下工作面示意

(6)

式中：Px，Py分别为成员在x，y方向的坐标；Xmin，Xmax分别为x坐标的最小值和最大值；Ymin，Ymax分别为y坐标的最小值和最大值；R1，R2为0～1的随机数。

2.2仿真结果

通过仿真获得所有成员疏散到避难硐室的时间为520 s，疏散过程中不同时刻成员的分布情况如图4所示(圆点表示疏散成员所处的位置)。同时通过仿真获取疏散人数、出口流量与疏散时间的关系曲线，分别如图5、图6所示。

(a) 0 s

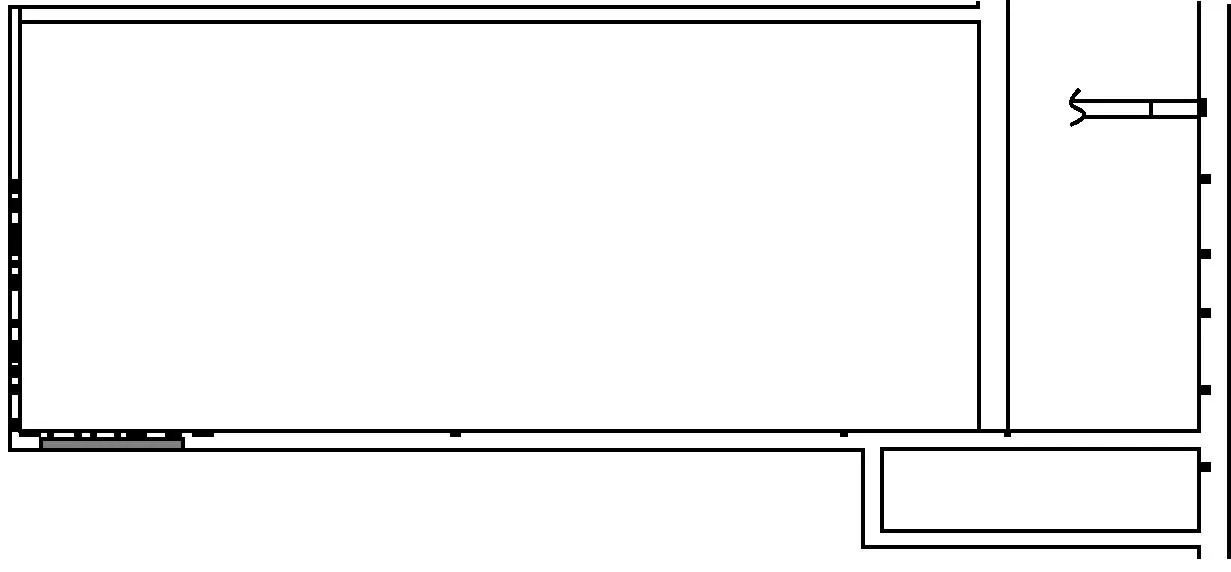
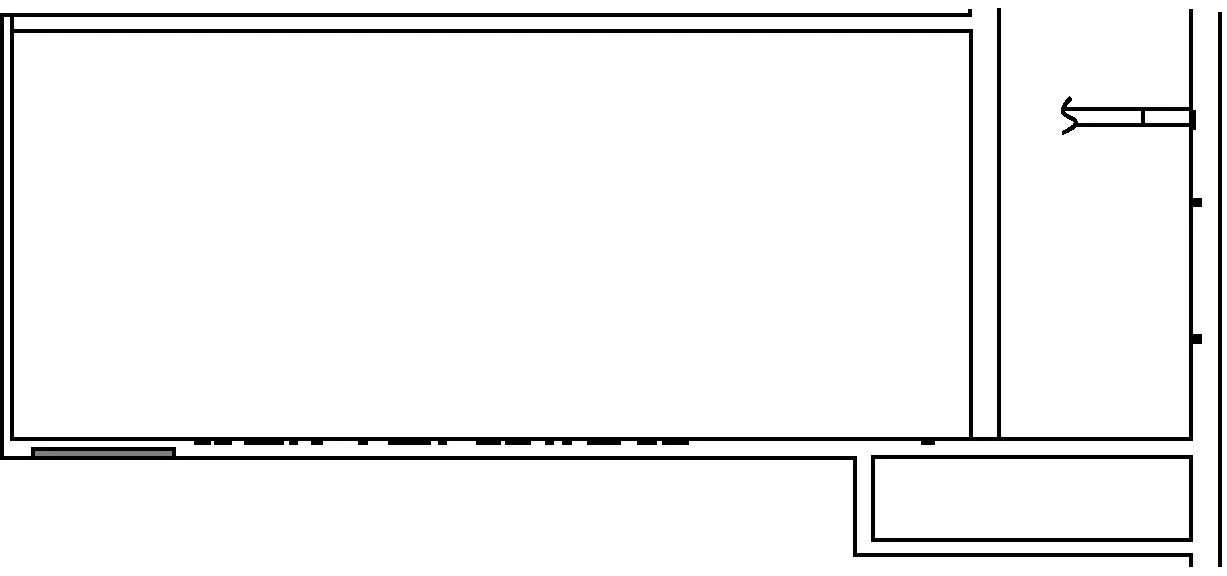
(b) 60 s

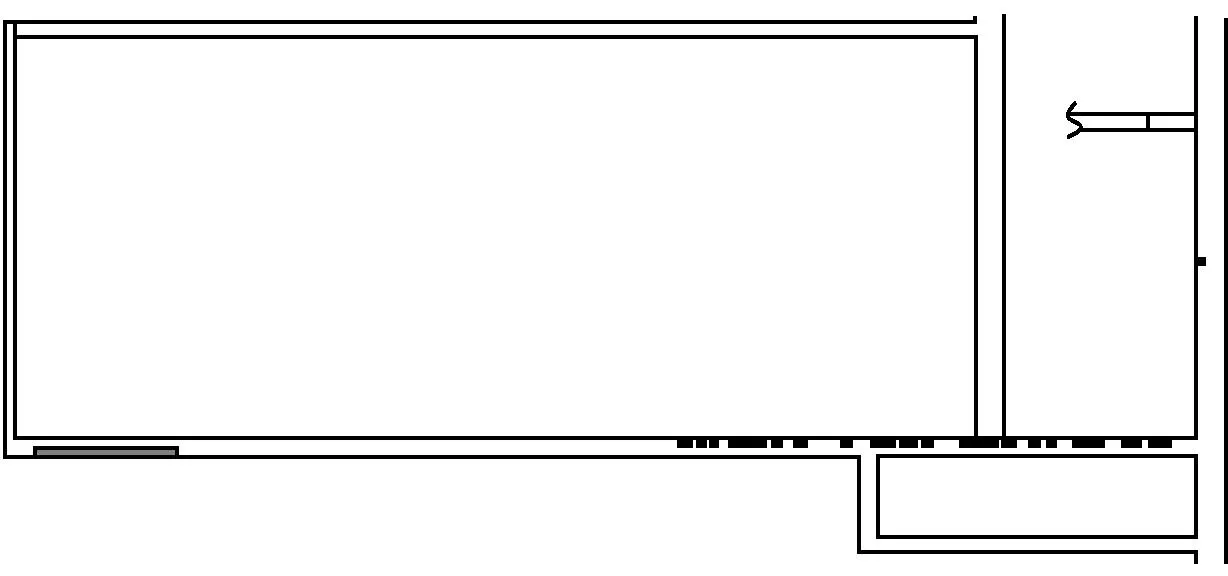
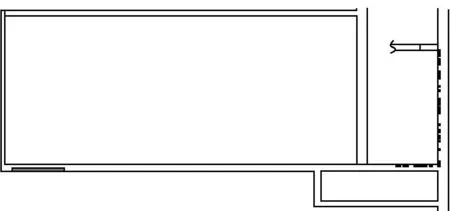
(d) 300 s

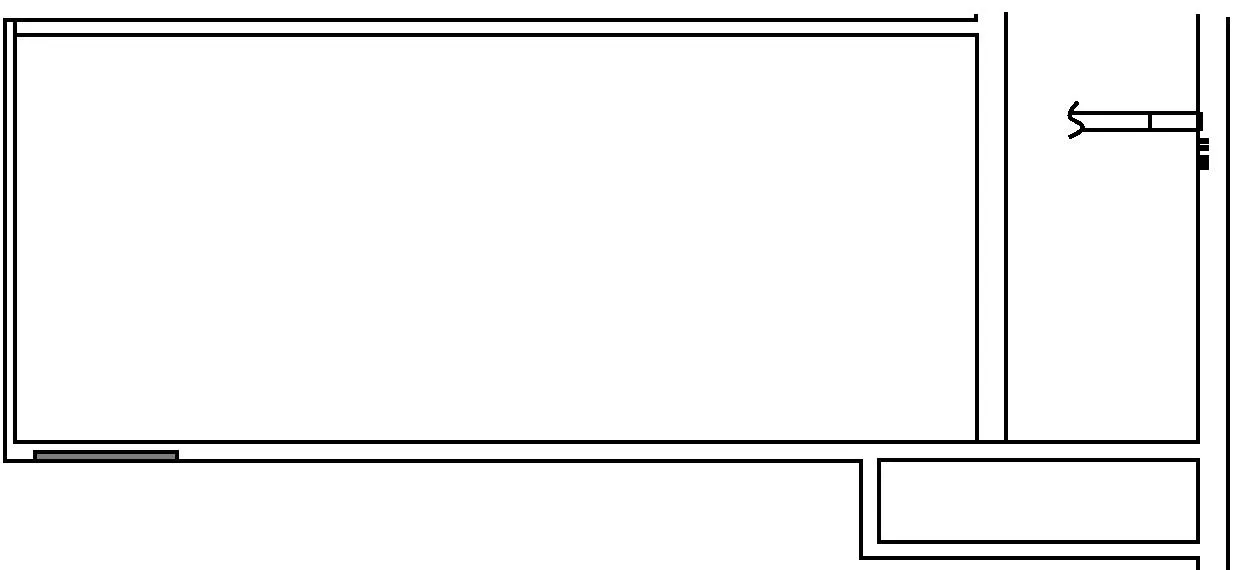
(f) 510 s

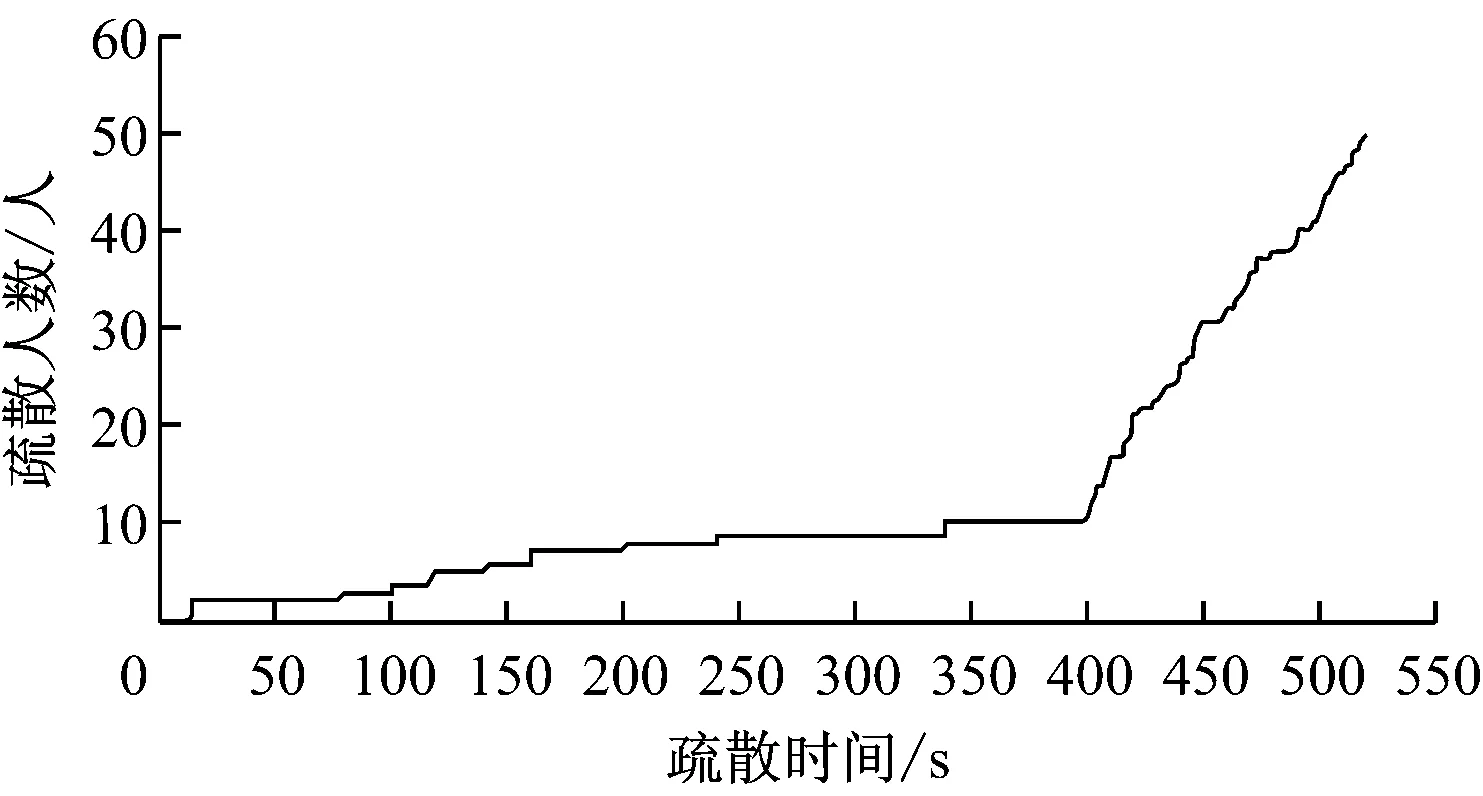
图5　疏散人数随时间变化曲线

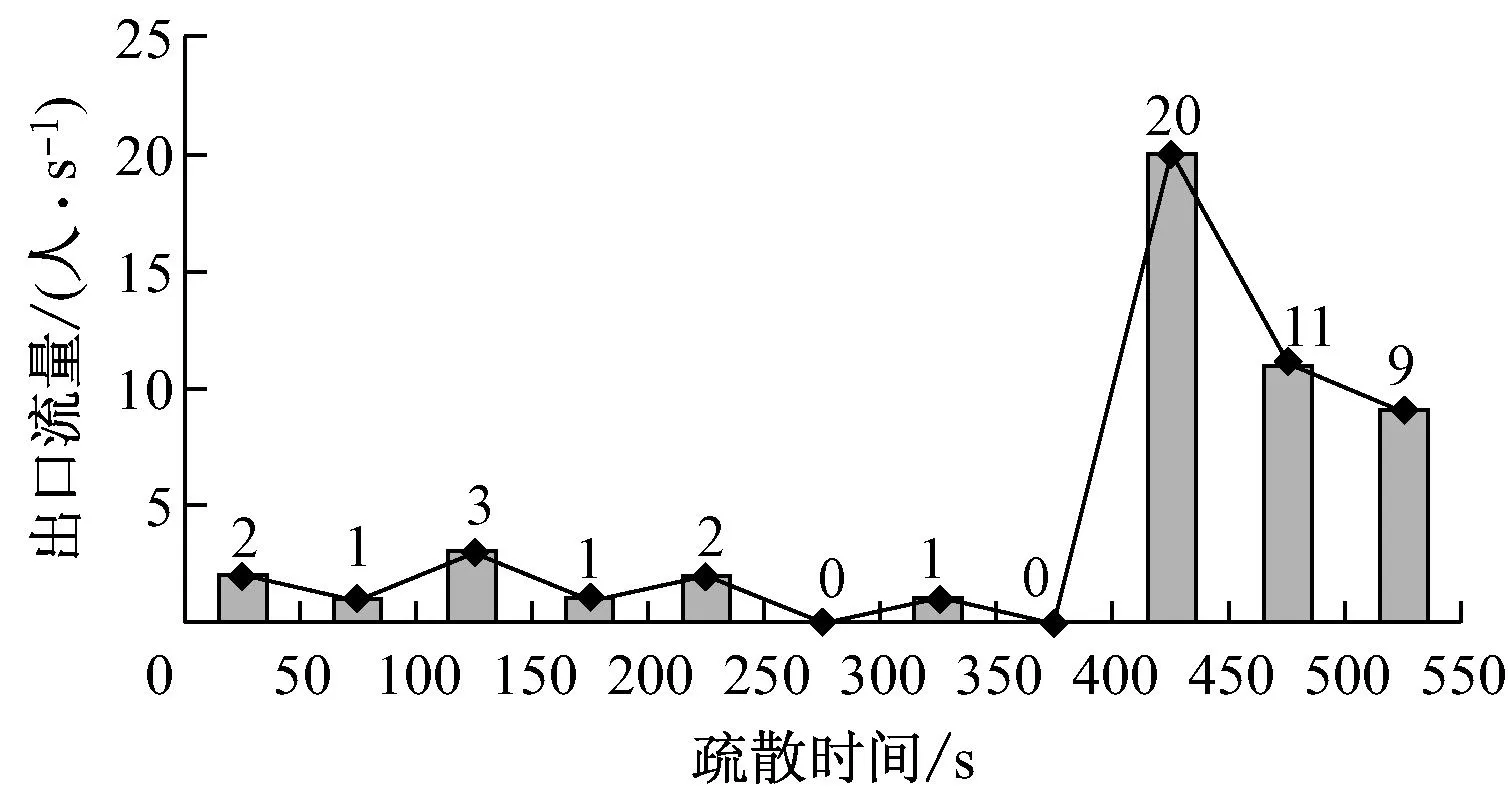
图6　出口流量随时间变化曲线

从图4和图6可看出，距避难硐室较近的位于主巷道和轨道运输巷的10个矿工在400 s内全部到达避难硐室，此阶段最大出口流量为3 人/s；从图5和图6可看出，400 s后疏散人数和出口流量急剧增加，400～450 s时出口流量达到最大为20人/s，整个仿真过程中疏散人数和出口流量激增主要集中在400～520 s，这是由于距离避难硐室最远的人员疏散时间最长，其决定了整个人群的疏散时间。

3结语

煤矿井下人员安全疏散模型中采用网格对疏散通道进行划分，通过设置“成员流势”模拟人员通过出口的路径选择，同时考虑安全疏散时成员响应时间、移动速度和周围环境的影响，从而能直观显示井下人员疏散过程的动态变化，获取人员疏散时间及各时刻出口流量，可帮助评估煤矿井下人员疏散的影响因素，并为制定安全疏散方案提供数据参考。

参考文献：

[1]李隆庭.基于井下避难硐室系统的煤矿应急模型研究[D].北京:首都经济贸易大学,2012.

[2]武爽,季经纬,赵平,等.基于数值模拟的矿井火灾疏散路径选取研究[J].中国煤炭,2011,37(10):89-92.

[3]杨雪,李占国,卢亚丽.多障碍情境下矿工紧急疏散建模及仿真[J].工业工程,2014,17(6):1-6.

[4]江成玉,李春辉,苏恒瑜.基于GIS的煤矿火灾救援管理系统设计[J].中国煤炭,2010,36(4):99-102.

[5]屈云超.密集人群疏散行为建模与动态特性研究[D].北京:北京交通大学,2015.

王宛平，李世豪.煤矿井下人员安全疏散建模与仿真[J].工矿自动化，2016,42(1)：20-23.

网络出版地址：http://www.cnki.net/kcms/detail/32.1627.TP.20151231.1553.007.html

Modeling and simulation of underground personnel safety evacuation

WANG Wanping1，LI Shihao2

(1.Department of Information Engineering, Henan Quality Polytechnic, Pingdingshan 467000, China;

2.College of Computer and Software Engineering, Pingdingshan Industrial College of Technology,

Pingdingshan 467001, China)

Abstract:In view of problem of underground personnel safety evacuation when accident occurs, an underground personnel safety evacuation model was established. Underground tunnels are divided into grids, and distance between the grids and evacuation exit is reflected by setting members potential flow, so as to determine moving direction and evacuation route of evacuees. Evacuation time is obtained through combination of moving speed and response time of evacuees and detection time of disaster. The simulation results show that the model can directly present dynamic process of evacuation and provide data reference for safety evacuation scheme.

Key words:underground evacuation; evacuation model; members potential flow; evacuation route; evacuation time

基金项目：山东省自然科学基金项目(ZR2012EEM021)。

作者简介：王宛平(1983-)，女，河南南阳人，讲师，硕士，主要研究方向为计算机技术，E-mail:707382401@qq.com。 公茂法(1959-)，男，山东蒙阴人，教授，博士研究生导师，主要从事电气测量技术、信号检测技术和电力系统自动化方面的研究工作，E-mail：1520837108@qq.com。通信作者：周立人(1992-)，男，山东邹城人，硕士研究生，研究方向为电力系统及其自动化，E-mail： 617209069@qq.com。

收稿日期：2015-09-22；修回日期：2015-12-15；责任编辑：盛男。 2015-10-15；修回日期：2015-11-20；责任编辑：张强。

中图分类号：TD77

文献标志码：A网络出版时间：2015-12-31 15:53

文章编号：1671-251X(2016)01-0020-04DOI:10.13272/j.issn.1671-251x.2016.01.007