影响篮球投篮命中率因素的模型建立与分析

覃云飞 韦金亮

【摘 要】运用运动生物力学的原理，搭建了影响篮球投篮命中因素间的关系模型，并利用函数理论与微分学原理具体分析了各因素间的关系。为提高篮球投篮的命中率提供理论基础，以期为篮球教练员（教师）、运动员、以及广大篮球爱好者提高投篮命中率提供建设性的意见。

【关键词】投篮  模型  因素  分析

【中图分类号】G  【文献标识码】A

【文章编号】0450-9889（2015）12C-0168-03

投篮是持球队员将球投入篮圈所采用的各种动作的总称。在篮球竞赛中，投篮是比赛的唯一得分手段，篮球运动所有进攻的技、战术，最终都是为投篮服务。影响投篮命中的因素很多，例如出手点与篮圈的水平、垂直距离、出手时间、出手速度、出手角度等。笔者在查阅相关文献时发现，前人主要研究了篮球出手速度与出手角度两者之间的关系，而影响投篮命中的因素除了以上两者之外还有很多。同时，篮球的出手速度是运动员对篮球的作用力产生的结果。运动员对篮球的作用力与出手时间共同决定着篮球的出手速度有多大。因此可推断篮球的出手速度与运动员投篮所给篮球的作用力有直接的关系，与运动员有间接的关系，然而运动员与对篮球的作用力之间又有直接的关系。不管是直接或者间接的关系，让运动员控制自己的发力大小与出手快慢比控制对篮球受力后篮球所获得的速度大小容易很多。因此，在分析影响投篮命中率的因素过程中，用运动员对篮球的发力与出手时间代替篮球的出手速度。本文将尝试对投篮建立模型并对影响投篮命中因素之间的关系进行分析。

一、模型的建立

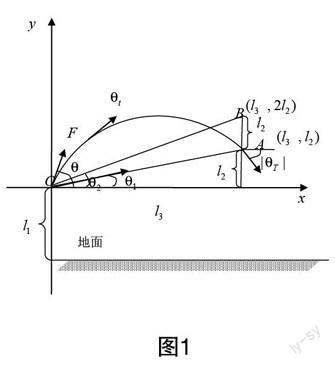
图1

以出手点为原点，平行、垂直于水平面的直线分别为x，y轴建立直角坐标系（如图1）。出手点高度记为l1，篮框与出手点的垂直距离记为l3，篮框与出手点的水平距离记为l2，出手时间记为t0。由于出手时间较短，所以我们认为投篮者给予篮球的力是均匀的，且记为F，篮球重为m，出手角度为，重力加速度为g，A点坐标为（l3，l2），B点坐标为（l3，2l2），线段OA，OB与x轴正半轴的夹角分别记为，。

相对而言阻力的作用较小，所以我们默认为没有阻力作用。

所有的分析都是基于以下两个假设：1.假设投篮命中;2.在每个分析中除了所分析的两个因素外其他因素都是固定不变的。

篮球从投篮者手中脱离之后到再次受到外力作用（如触碰篮板、碰地）之前的运动轨迹方程为

①

如果运动员想投篮命中，那么他必须让篮球经过点A，即存在某时刻T使得

②

根据①我们可以得到篮球在t时刻的速度方程为

③

设为t时刻篮球的运动方向，那么由③我们可以推出

④

由①可知从篮球离手时刻到t时刻篮球的重力势能变化量为

⑤

假设篮球离手后经过t1时间到达最高点，那么t1满足

⑥

同时，我们可以得到t1时刻投出去的篮球的重力势能与动能分别为

⑦

⑧

二、分析模型

分析1：运动员投篮命中关于出手角度的必要条件

由②与④可知篮球入圈瞬间的入射角度必满足

由于篮球规则中规定投篮命中必须是从篮圈上方进入篮圈而不可从下方进入篮圈，所以篮球入篮圈时刻一定是在篮球下落过程中的某一时刻。而下落过程中任意时刻t0的运动方向必须满足，所以有。从而我们可以得到要想投篮命中出手角度必须满足：

⑨

结论1：条件⑨告诉运动员：1.出手角度的大小取决于出手点与篮圈的水平、垂直距离l2，l3;2.出手角度需大于，即运动员发力方向应该指向OB的左上方（见图1）。

根据以上分析，我们得到是投篮命中的必要条件，所以在以下的分析中我们总是假设  。

分析2：运动员发力的大小与出手时间长短之间的关系

由②消去T可得

因为g，l3，m，t0都是大于0的常数，及，所以得到

由上面两式很显然可以得到，运动员所需发力F会随着出手时间t0的增长而减小，随着出手时间t0的缩短而增大。这告诉我们在篮球运动中某些过程也是遵守物理学中的动量守恒定律的。

结论2：篮球投篮的出手速度和发力大小呈反比的关系，对于出手比较快的运动员来说，他们要想投篮命中，就必须比出手慢的运动员发力大一些;同样，出手比较慢的运动员要想投篮命中，与出手快的运动员相比，他们需发力小一点。

分析3：运动员发力的大小与出手角度大小之间的关系

根据能量守恒定律得到

结合⑥式可以得到

从上式我们可以看出F在区间（00，900），关于出手角度是递增的，所以运动员投篮时出手角度越小越省力。然而在分析1中知道运动员要想投篮命中出手角度必须满足。因此运动员投篮时在保证出手角度的情况下越小越省力。

结论3：投篮时发力方向指向OB的左上方并与OB所构成的角度越小，越省力;只存在尽可能省力出手角度，而不存在最省力出手角度。

分析4：运动员所需发力和出手点与篮圈垂直距离l2之间的关系

由②式得到

⑩

对⑩式关于l2求微分得到，

所以F'﹥0，由此我们可以推出，F是一个关于l2是递增的函数，因而运动员所需发力F的大小随着出手点与篮圈的水平距离l2的增大而增大，减小而减小。

结论4：运动员投篮的出手点和发力大小呈反比关系。当运动员的出手点比较低时，在相对的范围内需要发较大的力;当运动员提高出手点时，由于惯性作用，其可以发小一点的力。

分析5：运动员所需发力F的大小与出手点与篮圈的水平距离l3大小之间的关系

对⑩式关于l3求微分，有

因为运动员的投篮都是以命中为目的，所以根据分析1可要求。由上式及可知，F'﹥0。因为F'﹥0，所以F是一个关于l3是递增的函数。因此，当时，运动员所需发力F的大小随着出手点与篮圈的垂直距离l3的增大而增大，减小而减小。

结论5：当运动员距离篮圈比较远时，该模型要求其投篮需要发较大的力以满足提高命中率的要求;当运动员投篮位置缩短与篮圈的距离时，F值应相对减小来符合该模型的要求。

分析6：出手角度和出手点与篮圈水平距离、垂直距离之间的关系

由②式可得，

（上接第169页）

由上式可以推出，出手角度关于l2是递增的，关于l3是递减的。

结论6：当出手点降低时，出手角度应该增大;当出手点增高时，出手角度应该减小;当运动员与篮圈的距离增大时，出手角度应该减小;当运动员与篮圈的距离缩短时，出手角度应该增大。

分析7：从球出手到球进圈所用时间与出手角度之间的关系

根据②式我们可以得到以下式子

由上式我们可以知道：T关于是递增的。

结论7：如果在比赛中想增加回合数（这种情况在NBA最后追分时候会经常发生），那么我们在保证能投篮命中的情况下可以试着尽量减小出手角度以缩短T以便达到增加回合数的目的。

篮球运动的核心在于将球命中篮筐。本文从运动生物力学和函数理论以及微分学原理出发，构建了影响篮球命中因素的模型并予以分析，每个分析与结论在理论层面均能对教授篮球或者学习篮球投篮的人给予一定的帮助。期望在动态的篮球投篮过程中，结合静态的模型并将各个值向模型修正靠拢，最终达到提高投篮命中率的目的。

【参考文献】

[1]孙民治.体育学院专修教材·篮球运动高级教程[M].北京：人民体育出版社，2000

【作者简介】覃云飞（1982- ），男，广西来宾人，壮族，广西体育高等专科学校讲师，硕士，研究方向：体育教育训练学。

（责编 丁 梦）