碳纤维增强环氧树脂复合材料加筋板的压缩屈曲特性

张浩宇，何宇廷，冯 宇，谭翔飞，邵 青，尹 翔

(1.空军工程大学航空航天工程学院， 西安 710038；2.陆航驻203所军事代表室， 西安 710038)



碳纤维增强环氧树脂复合材料加筋板的压缩屈曲特性

张浩宇1，何宇廷1，冯 宇1，谭翔飞1，邵 青1，尹 翔2

(1.空军工程大学航空航天工程学院， 西安 710038；2.陆航驻203所军事代表室， 西安 710038)

摘要：分别应用工程算法和有限元软件ANSYS对碳纤维增强环氧树脂复合材料加筋板的压缩稳定性进行了分析，得到了加筋板的临界失稳屈曲载荷和屈曲模态；同时对复合材料加筋板进行了压缩稳定性试验，并与计算结果进行了对比验证。结果表明：碳纤维增强环氧树脂复合材料加筋板具有后屈曲承载能力，其压缩破坏形式主要为筋条的脱胶、断裂和蒙皮的撕裂；工程算法结果、有限元计算结果与试验得到的临界屈曲载荷误差分别为13.8%和-15.5%，结果较吻合，证明了工程算法的正确性和有限元模拟方法的合理性。

关键词：复合材料加筋板；屈曲特性；压缩稳定性；有限元模型；工程算法

0引言

复合材料薄壁结构是工程中应用较广泛的一种结构，当其受面内压缩、剪切等载荷作用时，常见的失效模式为屈曲失稳[1-3]。因此，薄壁结构的屈曲失稳特性对工程应用影响重大。对于复合材料加筋板压缩屈曲失稳性能的研究，现阶段主要集中在试验研究、有限元模拟和工程算法三个方面[4]。试验研究结果普遍认为加筋板结构在发生屈曲以后并没有完全破坏，仍具有一定的承载能力，即有后屈曲强度；工程算法是基于经验公式的分析方法，因此具有一定局限性，分析时需要对加筋板结构及边界条件进行简化，有可能导致较大的误差；而有限元法可以较为准确地对复合材料加筋板的屈曲特性进行分析。国内外学者对加筋板的压缩屈曲性能已有一定研究，丁金涛等[5]建立了加筋板的等效刚度矩阵模型和各种屈曲模式下屈曲载荷和破坏载荷的数学模型，提出了一种针对多种组合形式的复合材料加筋板稳定性分析的工程计算方法；吴存利等[6]对复合材料波纹板在剪切载荷作用下的屈曲进行了工程计算，计算得到的屈曲载荷与试验结果较一致；孔斌等[7]通过有限元仿真研究了整体加筋板在后屈曲过程中的传载机制，计算结果与试验结果吻合较好，并指出导致加筋板失效的主要原因是筋条与蒙皮的脱粘分离；Bisagni等[8]应用神经网络算法和蚁群算法对加筋板的屈曲性能和后屈曲性能进行了优化设计；王春寿等[9]通过有限元软件ABAQUS研究了复合材料加筋盒段的后屈曲承载能力，发现在弯扭载荷下后屈曲诱发的盒段壁板/筋条界面的失效是界面脱胶而导致的。

为了研究复合材料加筋板的压缩屈曲特性，作者分别应用工程算法与有限元软件ANSYS研究了复合材料加筋板结构的压缩稳定性，并进行了压缩稳定性试验，将有限元计算结果、工程计算结果与试验结果进行了对比验证，为其工程应用提供有益参考。

1试样制备与试验方法

试验用复合材料加筋板的蒙皮和筋条材料均为单向带碳纤维增强环氧树脂复合材料(CCF300/5228A)，单层厚度为0.125 mm，力学性能如表1所示，表中E11，E22分别为材料在1，2弹性主方向上的弹性模量，G12为弹性方向平面内的剪切弹性模量，12为该平面内的泊松比。加筋板中蒙皮的铺层顺序为[45/45/0/0/0/-45/90/45/45/0/0/0/-45/90]s，筋条的铺层顺序为[0/0/45/0/0/-45/90/45/0/0/-45]s，筋条截面为工字型，几何尺寸如图1所示，相邻筋条间距150 mm。

表1　碳纤维增强环氧树脂复合材料力学性能参数Tab.1　Mechanical properties of the carbon fiber reinforcedepoxy resin composite

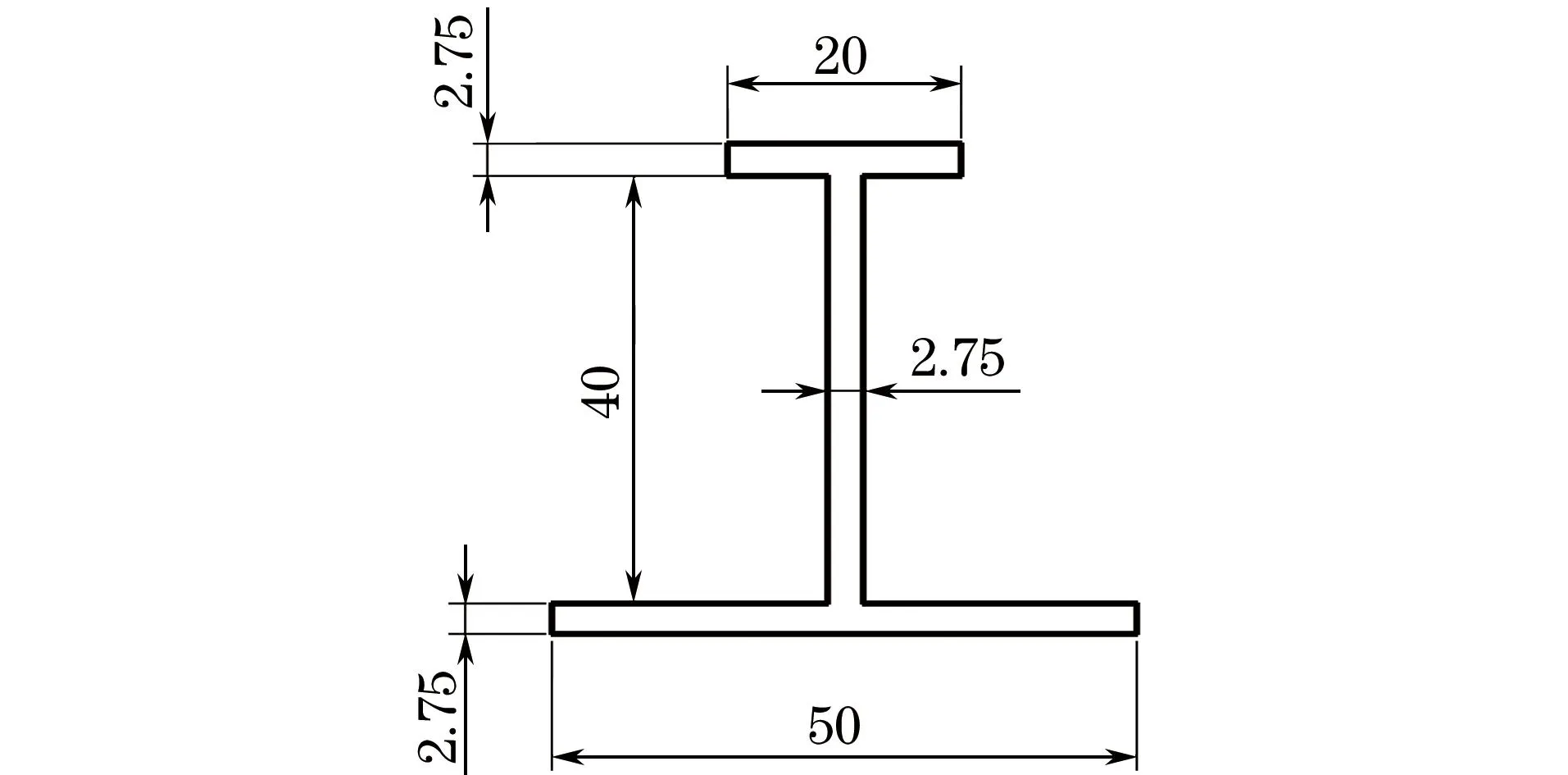
图1　筋条截面的形状和尺寸Fig.1　Section shape and size of the stiffener

压缩试样截取自复合材料加筋板，尺寸为600 mm(宽)×820 mm(长)，如图2所示，试样两端端部进行灌胶处理作为加载段。

图2　压缩试样实物形貌Fig.2　Appearance of the compression specimen

在WAW-3000B型结构试验平台上进行压缩稳定性试验，加载控制系统采用MTS FLEX TEST40型三通道控制器。试验前在试样的筋条间蒙皮及筋条上粘贴应变计，通过低载荷预试验对各测试点的应变进行测量，根据测量值调整试样及夹具安装位置，保证试样均匀承受压缩载荷。正式试验开始后，在试样上逐级施加压缩载荷，参考有限元计算结果，取每级载荷为50 kN，并通过应变仪记录各测试点的应变，夹具安装和加载方式如图3所示。

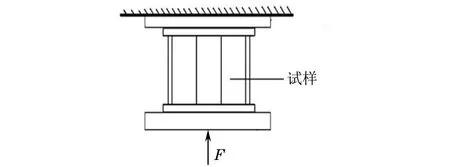
图3　加载方式示意Fig.3　Schematic of loading method

2局部屈曲载荷的工程计算

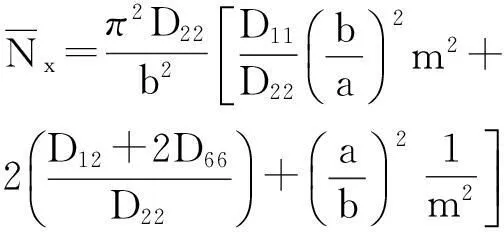
(1)

式中：a，b分别为筋条间蒙皮的长度与宽度；D11，D12，D22，D66分别为蒙皮弯曲刚度系数；m为蒙皮长度方向上屈曲的半波数，m=1，2，3,…。

将蒙皮的长度、宽度、弯曲刚度系数代入式(1)，计算得到不同半波数下蒙皮的局部弯曲载荷，绘制x-m曲线，如图4所示。

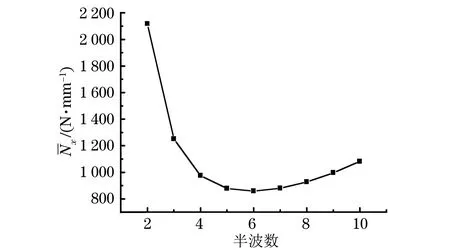
图4　式(1)计算得到的蒙皮x-m曲线Fig.4　x-m curves of skin calculated by Eq.(1)

3局部屈曲载荷的有限元计算

应用有限元软件ANSYS对复合材料加筋板结构进行线性屈曲模拟[11-14]。按照试样的实际尺寸选择壳单元(SHELL99)建立有限元模型，通过扫掠生成网格，将筋条按直接固接于蒙皮上进行整体建模。有限元模型一端固定,另一端施加均布的压缩载荷，固定端的6个自由度都约束为0，加载端将除加载方向的自由度外都约束为0；将侧边的面外法向位移约束为0，防止加筋板侧边首先出现弯曲，有限元模型及边界条件如图5所示。加载端共177个节点，在所有节点上均施加100 N的压缩载荷，共加载17 700 N。

图5　复合材料加筋板有限元模型Fig.5　Finite element model of the composite stiffened panel

有限元软件提取得到特征屈曲λ为39，根据式(2)计算得到临界屈曲载荷Fcr。

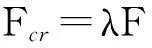
(2)

式中：F为施加的压缩载荷。

由式(2)计算得到加筋板的临界屈曲载荷为690.3 kN。从图6中可以看出，加筋板的一阶屈曲模态是蒙皮的局部屈曲，横向半波数为3，纵向半波数为6，这与半波数为6时式(1)计算的x最小值是相符的，证明了模型的合理性。

图6　复合加筋板压缩一阶屈曲模态Fig.6　First-order buckling mode of the composite stiffened panel

4试验结果与讨论

在复合材料加筋板压缩试验过程中，当载荷在450 kN以下时没有任何异常；当载荷加载至450 kN时，可听到试样内部发出轻微的响声，随着载荷的增加轻微响声持续发生；当载荷达到600 kN时，可观察到蒙皮发生变形，试样发生失稳；加载至860 kN时，试样发出了较大的响声，持续30 s后仍能继续承载，与文献[15-18]的现象相似；当加载至960 kN时，试样突然发出巨大的响声，筋条与蒙皮发生脱胶撕裂，试样发生破坏，不能继续承载。破坏形式主要是蒙皮撕裂和筋条的断裂、脱粘，如图7所示。

图7　复合材料加筋板压缩破坏宏观形貌Fig.7　Failure macrograph of the composite stiffened panelafter compression: (a) specimen 1# and (b) specimen 2#

加筋板试样的压缩试验结果列于表2。从表2可以看出试验结果的分散性较小，加筋板的平均破坏载荷是平均临界屈曲载荷的1.62倍，说明其后屈曲承载能力较强。

加筋板的临界屈曲载荷工程计算结果为515 kN，有限元计算结果为690.30 kN，根据文献[19]中的相对误差计算公式可得到两者与试验值的相对误差分别为13.8%，-15.5%，由此可见，加筋板临界屈曲载荷的有限元计算值、工程计算值与试验值误差较小。

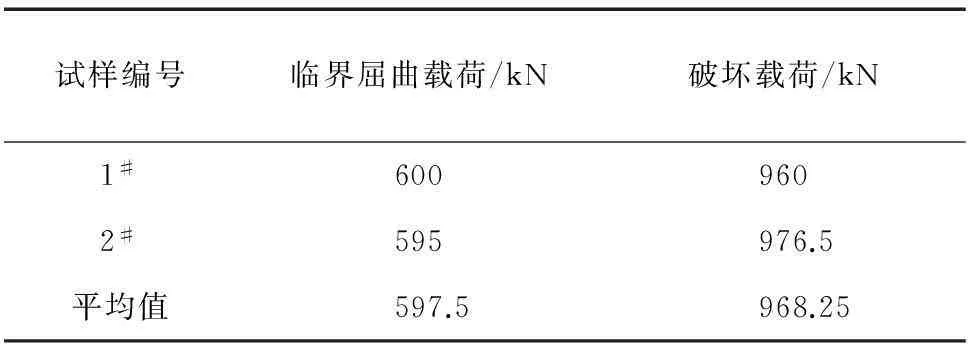
表2　加筋板压缩试验结果Tab.2　Experimental results of the stiffened panelunder compression

5结论

(1) CCF300/5228A碳纤维增强环氧树脂复合材料加筋板在压缩载荷下的失稳形式主要表现为蒙皮的局部屈曲，其破坏形式主要为筋条的脱粘、断裂及蒙皮的撕裂。

(2) 复合材料加筋板在压缩载荷下有较大的后屈曲承载能力，其破坏载荷是临界屈曲载荷的1.62倍，因此对于复合材料加筋板结构应充分利用其后屈曲承载能力。

(3) 临界屈曲载荷工程计算值、有限元计算值与试验结果吻合较好，因此可以将工程计算方法和有限元法应用到其结构屈曲载荷的计算中，为加筋板工程应用提供参考。

参考文献：

[1]王平安,矫桂琼,王波,等.复合材料加筋板在剪切载荷下的屈曲特性研究[J].机械强度, 2009,31(1):78-82.

[2]ATEVENS K A，RICCI R,DAVIES G A O. Buckling and post-buckling of composite structures[J]. Composites, 1995,26(3):189-199.

[3]MEZGHANI K. Long term environmental effects on physical properties of vinylester composite pipes[J]. Polymer Testing, 2012,31(1):76-82.

[4]万玉敏,张发,竺铝涛,等.泡沫夹层复合材料与复合材料层合板低速冲击性能的比较[J].机械工程材料, 2014,38(7):90-94.

[5]丁金涛,唐应伟,金天国,等.复合材料加筋板失稳分析的工程计算方法研究[J].兵器材料科学与工程, 2015,38(1):44-49.

[6]吴存利,段世慧,李新祥.复合材料波纹板剪切载荷作用下的屈曲试验与分析[J].航空学报, 2011,32(8):1453-1460.

[7]孔斌,叶强,陈普会,等.复合材料整体加筋板轴压后屈曲的传载机制[J].复合材料学报, 2010,27(5):142-149.

[8]BISAGNI C, LANZI L. Post-bucklingoptimisation of composite stiffened panels using neural networks[J]. Composite Structures, 2002,58(2):237-247.

[9]王春寿,陈普会,隋晓东,等.复合材料多墙盒段的设计与后屈曲性能[J]. 复合材料学报, 2013,30(5):174-179.

[10]PAIK J K, SEO J K. Nonlinear finite element method models for ultimate strength analysis of steel stiffened-plate structures under combined biaxial compression and lateral pressure actions—part Ⅱ：stiffened panels[J]. Thin-Walled Structures, 2009,47(8/9):998-1007.

[11]WANG D, ABDALLA M M. Global and local buckling analysis of grid-stiffened composite panels[J]. Composite Structure, 2015,119:767-776.

[12]谢可勇,李晖,孙岩,等.湿热老化对纤维增强树脂基复合材料性能的影响及其机理[J].机械工程材料, 2014,38(8):1-5.

[13]陈涛,何宇廷,邵青,等.湿热环境对纤维增强树脂基复合材料加筋板剪切性能的影响[J].机械工程材料, 2014,38(4):59-62.

[14]冯宇,何宇廷,邵青,等.湿热环境对复合材料加筋板压缩性能的影响[J].机械工程材料, 2015,39(1):73-76.

[15]OWENS G A, SCHOFIELD S E. Thermal cycling and mechanical property assessment of carbon fibre fabric reinforced PMR-15 polyimide laminates[J]. Composites Science and Technology, 1988,33(3):177-190.

[16]ZHANG A, LI D, LU H, et al. Qualitative separation of the effect of voids on the bending fatigue performance of hygrothermal conditioned carbon/epoxy composites[J]. Materials and Design, 2011,32(10):4803-4809.

[17]卞栋梁,李曙林,常飞,等.损伤位置对复合材料加筋壁板轴压承载能力的影响[J].机械工程材料, 2014,38(9):95-98.

[18]中国航空研究院.复合材料结构设计手册[M].北京:航空工业出版社, 2001:340-364.

[19]JEDIDI J, JACQUEMIN F, VAUTRIN A. Design of accelerated hygrothermal cycles on polymer matrix composites in the case of a supersonic aircraft[J]. Composite Structure, 2005,68(4):429-437.

Compressive Buckling Property of Carbon Fiber Reinforced Epoxy Resin

Composite Stiffened Panel

ZHANG Hao-yu1, HE Yu-ting1, FENG Yu1, TAN Xiang-fei1, SHAO Qing1, YIN Xiang2

(1.Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi′an 710038, China;

2.Military Representative Office of Army Aviation in No.203 Institute, Xi′an 710038, China)

Abstract:The compression stability of carbon fiber reinforced epoxy resin composite stiffened panel was analyzed by the engineering method and finite element model (FEM) respectively, and the critical buckling load and buckling mode of the stiffened panel were obtained. The experiments on the compression stability of the composite stiffened panel were conducted and the experimental results were compared with the calculated results. The results show that the composite stiffened panel had a certain post-buckling carrying capacity, and the failure mode consisted of the adhesive failure and fracture of stiffener and the tearing of skin. The error between the critical buckling load calculated by the engineering method and FEM method and that of experiment was 13.8% and -15.5% respectively. The results agreed well, indicating the accuracy of the engineering method and the reasonableness of the finite element model.

Key words:composite stiffened panel; buckling property; compression stability; finite element model; engineering method

中图分类号：V258

文献标志码：A

文章编号：1000-3738(2015)12-0059-04