掺杂氮化铝中局域磁矩的第一性原理计算
2016-01-29
杨 红,全秀娥
(吉首大学物理与机电工程学院,湖南 吉首 416000)
掺杂氮化铝中局域磁矩的第一性原理计算

杨红,全秀娥
(吉首大学物理与机电工程学院,湖南 吉首 416000)
摘要:理想的稀磁半导体具有良好的室温铁磁性,氮化铝(AlN)稀磁半导体虽然具有宽的带隙和透光性,但由实验重复性差等原因,一直未得到广泛的应用.采用基于密度泛函理论的第一性原理方法计算掺杂硼(B)的AlN中局域磁矩的变化规律.通过分析电子结构发现,掺杂B后的AlN稀磁半导体中出现了明显的局域磁矩,其大小为2 μB.
关键词:稀磁半导体;氮化铝(AlN);第一性原理
稀磁半导体(Diluted Magnetic Semiconductors,DMS)能实现在同一材料中同时操控电子的电荷和自旋,故又称稀释磁性半导体,该材料由磁性过渡族余属元素或者稀土金属元素甚至非磁性金属元素替代Ⅱ-Ⅳ族、Ⅳ-Ⅵ族、Ⅱ-Ⅴ族、Ⅲ-Ⅴ族等半导体中的非磁性元素后形成的[1-3].实验中发现在一些半导体材料和氧化物,用非过渡金属掺杂也可以获得室温下的铁磁性,这预示着新的一类稀磁半导体和新的磁相互作用机理.氮化铝(AlN)是一种Ⅲ-Ⅴ族直接带隙宽禁带化合物半导体材料,在常温常压下的稳定相是六方纤锌矿结构,具有许多优异的物理性能(高击穿场强、高热导率、高电阻率、高化学稳定性和高热稳定性),是研究稀磁半导体磁性来源和机理的理想体系.笔者利用基于密度泛函理论和局域密度近似的第一性原理,分析了掺杂B后的AlN中局域磁矩的变化规律.
1第一性原理计算方法

图1 掺杂B后AlN的结构
采用基于密度泛函程序和广义梯度近似的第一性原理分析方法[4-6],其波函数用平面波展开,截断能设为330 eV,电子和离子间的相互作用采用缀加投影波势描述,氮化铝(AIN)晶格常数a=b=0.311 nm,c=0.498 nm,c/a=1.601,每个铝或氮原子都与相邻原子组成以其为中心的正四面体结构.AIN的掺杂是由原子硼(B)替换原子N实现的,选用的超胞中有16个Al原子和16个N原子,16个N原子中有1个被B原子替换,如图1所示,这相当于掺杂质量分数为6.25%.在布里渊区,以Г点为中心对7×7×5网格进行采样.在结构弛豫中,对每个原子位置进行优化,使其受力小于0.1 GeV/m.
2计算结果
AlN掺杂B后的总态密度如图2所示(实线代表自旋向上,虚线代表自旋向下,费米能级在能量为0 eV的地方,下同).由图2可知,掺杂B后的AlN的态密度自旋向上和向下的态是不对称的,尤其在费米能级附近特别明显.在原来的AlN的带隙中出现了杂质态,这说明体系是自旋极化的.掺杂B原子的分态密度见图3.从图3不难发现,自旋极化集中在B原子的p态上,且B原子的电子态与体系的价带重叠很少,其在带隙中的p态非常窄,说明B原子的价电子是很局域的,同时也说明B原子与体系的相互作用有限.
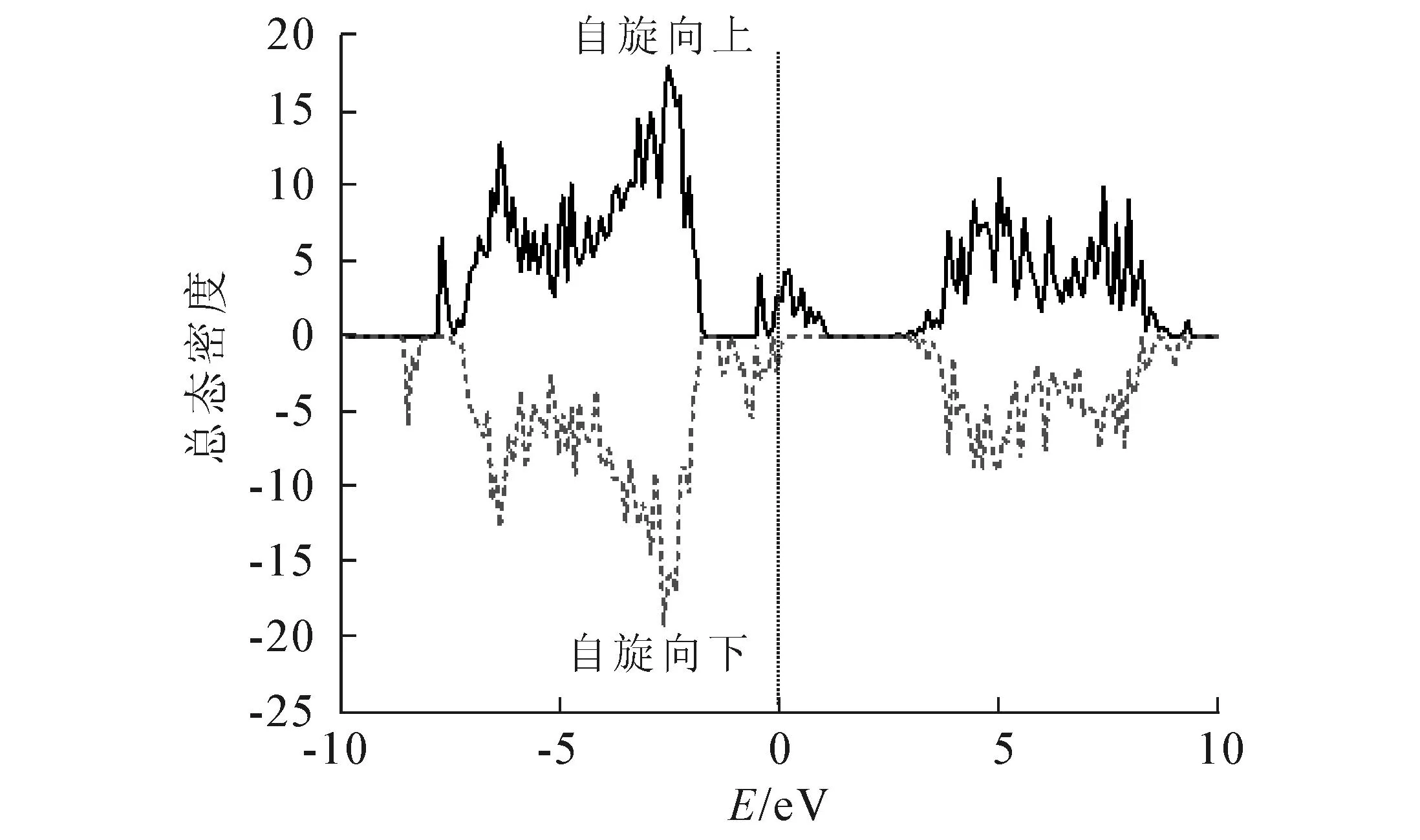
图2 掺杂B后AlN的总态密度
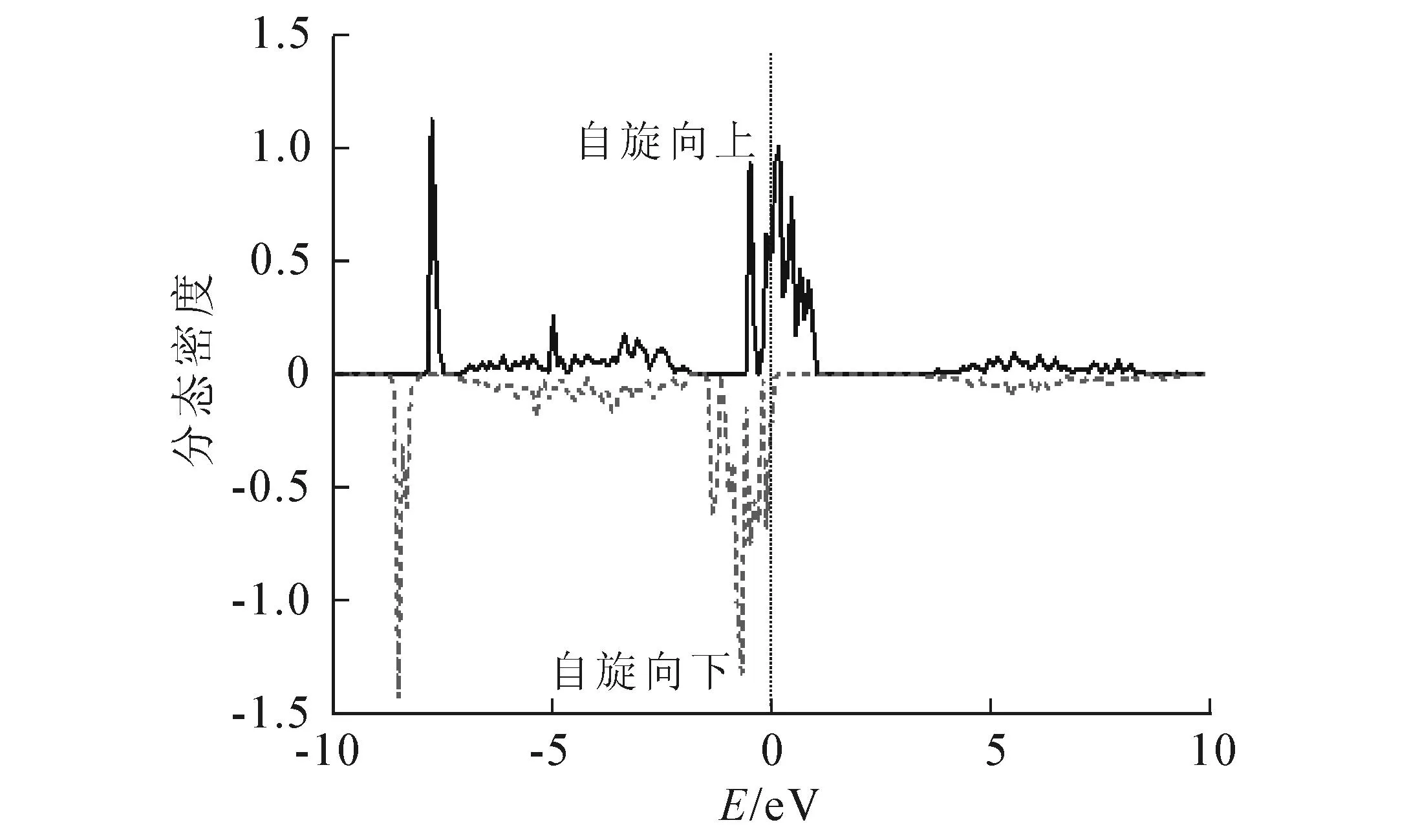
图3 B原子的分态密度

图4 体系的自旋电荷密度分布
体系的自旋电荷密度(自旋向上的电荷密度与自旋向下的电荷密度之差)分布如图4所示.从图4中不难发现,自旋电荷密度大部分都集中在B原子上,并且只在其近邻的Al原子和N原子上略有分布,在更远的Al和N原子上几乎没有分布.这说明在掺B后的AlN体系中,自旋几乎局限于B原子上,而在Al和N原子上自旋极化很小,从图3中B原子邻近Al和N的分态密度上也可以看出.由于N原子的电负性比Al的要大很多,每个N原子从Al原子获得1个电子,形成离子键.同样,B原子的电负性比Al大很多,每个B原子从Al获得1个电子.B原子有6个p轨道(3个自旋向上3个自旋向下),2个2p电子占据自旋向上的3个轨道中的1个.掺杂原子B获得2个电子后,3个自旋向上的态完全被占据,1个自旋向下的态也被占据,其净自旋为2 μB,与计算得出的总磁矩2 μB相符.
掺杂质原子的电子态主要由2p态和AlN的电子态共同相互作用而成.B的电负性介于Al和N之间,假设掺杂原子是N本身,那么它与宿主能带相互作用形成键态,进入宿主的价带和导带.当掺杂原子是B时,B原子的电负性比N原子的小,与宿主的相互作用比N原子与宿主的相互作用弱,B原子与宿主价带(导带)相互作用形成的反键态不足以被推入宿主的导带(价带)中,于是B原子的2p态就留在宿主带隙中.为了减少电子库仑力相互作用的能量,其2p态通过自旋极化来避免电子的接近,所以掺杂B原子是自旋极化的.
3结语
采用基于密度泛函理论和局域密度近似的第一性原理分析了掺杂B后的AlN中局域磁矩的变化规律,分析了掺杂体系的总态密度和掺杂原子的分态密度.计算结果表明,B原子电子态位于宿主的带隙中,非常局域且具有自旋极化.
参考文献:
[1] OHNO H.Making Nonmagnetic Semiconductors Ferromagnatic[J].Science,1998,281:951-956.
[2] DIETL T,OHNO H,MATSUKURA F,et al.Zener Model Description of Ferromagnetism in Zinec Blende Magnetic Semiconductors[J].Science,2000,287(5 455):1 019-1 040.
[3] 王颖,湛永钟,许艳飞,等.稀磁半导体材料的研究进展及应用前景[J].材料导报,2007,21(7):20-23.
[4] KRESSE G,HAFNER H.Ab Initio Molecular Dynamics for Open ̄Shell Transition Metals[J].Physical Review B,1993,48(17):13 115-13 118.
[6] BLÖCHL P E.Projector Augmented Wave Method[J].Physical Review B,1994,50(24):17 953-17 979.
(责任编辑陈炳权)
A First Principle Study of Local Magnetic Moment on
Non ̄Magnetic Elements Doped AlN
YANG Hong,QUAN Xiu’e
(College of Physics and Mechanical & Electrical Engineering,Jishou University,Jishou 416000,Hunan China)
Abstract:The ideal diluted magnetic semiconductors has favorable room ̄temperature ferromagnetism.Although AlN diluted magnetic semiconductor has wide band gap and good light ̄admitting quality,it has not been widely applied due to the unsatisfactory replicability of the experiment.Based on first principle of the density functional theory,we calculate the electric structure of AlN semiconductors doped by B element.The analysis of the calculated electric structure displays that an evident local magnetic moment change arises on doped AlN semiconductors.The magnitude of the local magnetic moment is 2 μB.
Key words:diluted magnetic semiconductors;AlN;first principle
作者简介:杨红(1980—),男,湖南浏阳人,吉首大学物理与机电工程学院讲师,博士,主要从事计算物理研究.
基金项目:湖南省教育厅科学研究项目(14C0939);吉首大学引进博士人才资助项目(jsdxrcyjkyxm201309);吉首大学教改课题资助项目(2014SYJG015)
收稿日期:2015-02-16
中图分类号:O162
文献标志码:A
DOI:10.3969/j.cnki.jdxb.2015.03.008
文章编号:1007-2985(2015)03-0032-03
