一类矩阵方程组的正交投影迭代解法

周富照，田时宇，袁艳杰

(长沙理工大学数学与计算科学学院，湖南 长沙 410004)



一类矩阵方程组的正交投影迭代解法

周富照，田时宇，袁艳杰

(长沙理工大学数学与计算科学学院，湖南 长沙 410004)

摘要：讨论了矩阵方程组AX=B，XC=D一般解的正交投影迭代解法.利用正交投影原理和一般矩阵的结构、性质构造迭代算法，再利用矩阵的奇异值分解、F-范数的正交不变性及矩阵方程组解的性质，证明了算法的收敛性，且推导出收敛速率的估计式.经数值实例验证了算法的有效性.

关键词：矩阵方程组；一般解；正交投影迭代法；最佳逼近解；极小范数解

为了叙述方便，先介绍一些记号.用Rm×n表示m×n实矩阵的集合，A⊗B表示矩阵A和B的Kronecker积，vec(A)表示将矩阵A按行拉直构成的列向量，tr(A)表示A的迹.对A,B∈Rm×n，A与B的内积定义为A,B=tr(BTA)，由此内积导出的范数‖A‖，即矩阵A的Frobenins范数.

考虑如下问题：

问题Ⅰ给定A∈Rp×m,B∈Rp×n,C∈Rn×l,D∈Rm×l,S⊆Rm×n，求X∈S，使得

(1)

(2)

问题Ⅰ与问题Ⅱ就是约束矩阵方程组问题及其最佳逼近问题，来源于左右逆特征对问题，在循环理论等领域有广泛的应用[1].近几年，国内外众多学者对该问题的研究取得许多成果.如文献[2]利用矩阵的广义逆，就S为一般实矩阵集合研究了问题有解的条件及其解的表达式；文献[3-4]借助于矩阵的奇异值分解及矩阵的广义逆，就S为对称正定矩阵集合、自反矩阵集合、反自反矩阵集合、广义自反矩阵集合等给出了问题有解的充分必要条件及其通解的表达；文献[5]借助于拉直算子及线性方程组的迭代思想，就S为一般实矩阵集合研究了问题的迭代解法；文献[6]就S为一般实矩阵集合、对称矩阵集合、反对称矩阵集合、中心对称矩阵集合等研究了矩阵方程组A1XB1=C1,A2XB2=C2的广义共轭梯度迭代解法.

迄今为止，关于问题Ⅰ的正交投影迭代解法的研究文献尚未见到.笔者主要就问题Ⅰ和问题Ⅱ的正交投影迭代解法进行研究.

1问题Ⅰ的迭代解法

首先给出求解问题Ⅰ的算法.

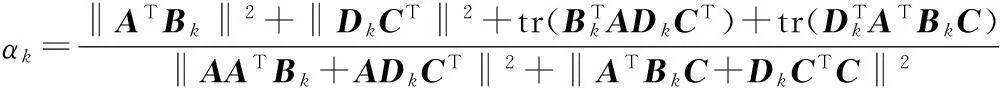
(ⅲ) 令ΔXk=αk(ATBk+DkCT)；

(ⅳ)当ΔXk充分小时，迭代结束，输出结果，否则，令Xk+1=Xk+ΔXk；

其次介绍如下几个引理：

引理1[5]矩阵方程组(1)有解的充要条件是B=AA+B,D=DC+C且BC=AD.

证明(ⅰ)由算法1可知，对∀k=0,1,2,…,都有BkC=BC-AXkC，ADk=AD-AXkC.又由引理1，BkC=BC-AXkC=AD-AXkC=ADk.

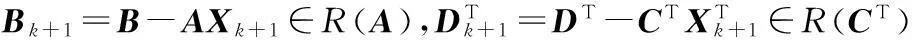
引理3在迭代算法1中，αk的值使得：

(ⅰ)‖Rk+1‖极小；

(ⅱ)Rk+1和ΔRk相互正交且‖Rk+1‖2=‖Rk‖2-‖ΔRk‖2(即Rk+1，ΔRk，Rk构成直角三角形，Rk是斜边).

证明(ⅰ) 利用算法1，有

‖Rk+1‖2=‖Rk-ΔRk‖2=Rk-ΔRk,Rk-ΔRk

2αk+

易知使‖Rk+1‖达到极小的充要条件是

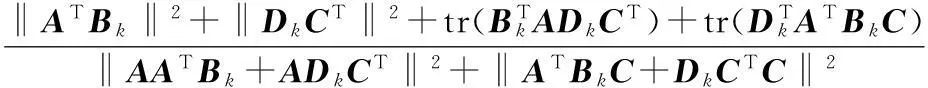
(ⅱ)利用算法1，有

Rk+1,ΔRk=Rk-ΔRk,ΔRk=αk-

若Rk+1和ΔRk相互正交，则可推出

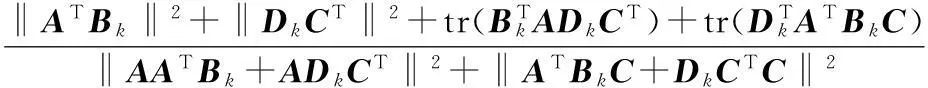
反之亦然.由Rk+1和ΔRk相互正交，有‖Rk‖2=‖Rk+1‖2+‖ΔRk‖2，即‖Rk+1‖2=‖Rk‖2-‖ΔRk‖2.

最后讨论算法1的收敛性.

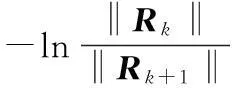
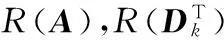
设θ是矩阵Rk和矩阵ΔRk的夹角，有

两组患者在出院时空腹血糖值比较，差异无统计学意义（P＞0.05）；出院后3个月时，两组空腹血糖值比较，差异具有统计学意义（P＜0.05），见（表1）。

其中

‖ATBk‖2+‖DkCT‖2+‖ADk‖2+‖BkC‖2=‖VETUTUGPPT‖2+‖VVTHQTQFTPT‖2+

‖UEVTHQT‖2+‖UGPFQT‖2=‖ETGP‖2+‖VTHFT‖2+

‖EVTH‖2+‖GPF‖2=‖ETY‖2+‖ZFT‖2+‖EZ‖2+‖YF‖2=

‖AATBk+ADkCT‖2≤2‖AATBk‖2+2‖ADkCT‖2=2‖AATBk‖2+2‖BkCCT‖2=

2‖UEVTVETUTUGPPT‖2+2‖UGPFQTQFTPT‖2=

2‖EETGP‖2+2‖GPFFT‖2=2‖EETY‖2+2‖YFFT‖2=

同理可得，

‖ATBkC+DkCTC‖2≤2‖ATBkC‖2+2‖DkCTC‖2=2‖ATADk‖2+2‖DkCTC‖2=

2‖VETUTUEVTHQT‖2+2‖VVTHQTQFTPTPFQT‖2=

2‖ETEVTH‖2+2‖VTHFTF‖2=2‖ETEZ‖2+2‖ZFTF‖2=

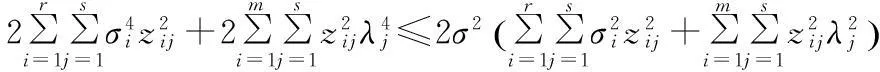
‖Bk‖2+‖Dk‖2=‖UGPPT‖2+‖VVTHQT‖2=‖GP‖2+‖VTH‖2=

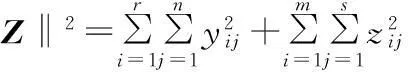
则

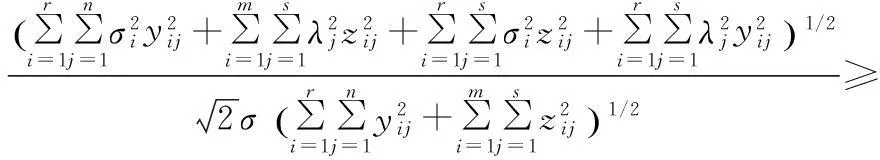
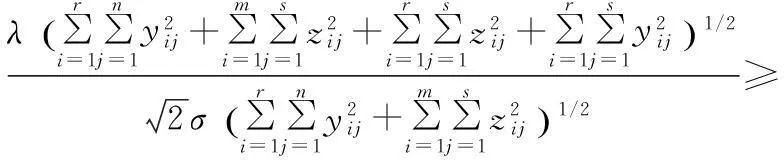
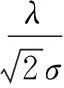
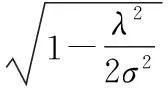
引理4[7]设线性方程组My=b存在解y0∈R(MT)，则y0必为该线性方程组的唯一的极小范数解.

定理2设问题Ⅰ相容，若取初值X0=ATW1+W2CT，其中W1为任意Rp×n矩阵，W2为任意Rm×l矩阵，则算法1收敛到该问题的极小范数解.

证明由定理1可知算法1收敛到问题Ⅰ的一个迭代解X*，且若取初值X0=ATW1+W2CT，其中W1为任意Rp×n矩阵，W2为任意Rm×l矩阵，则X*可表示为X*=ATN1+N2CT.

下面证明X*即为问题Ⅰ的极小范数解.

记wec(X)=x,vec(B)=b,vec(D)=d，则矩阵方程组(1)等价于线性方程组

(2)

又记vec(X*)=x*,vec(N1)=n1,vec(N2)=n1，则

再根据引理4可知x*是线性方程组(2)的极小范数解，由拉直映射同构，故X*是问题Ⅰ的极小范数解.

2问题Ⅱ的解

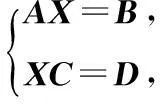
3数值实例

例1设

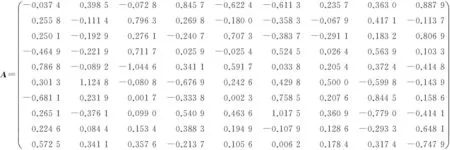
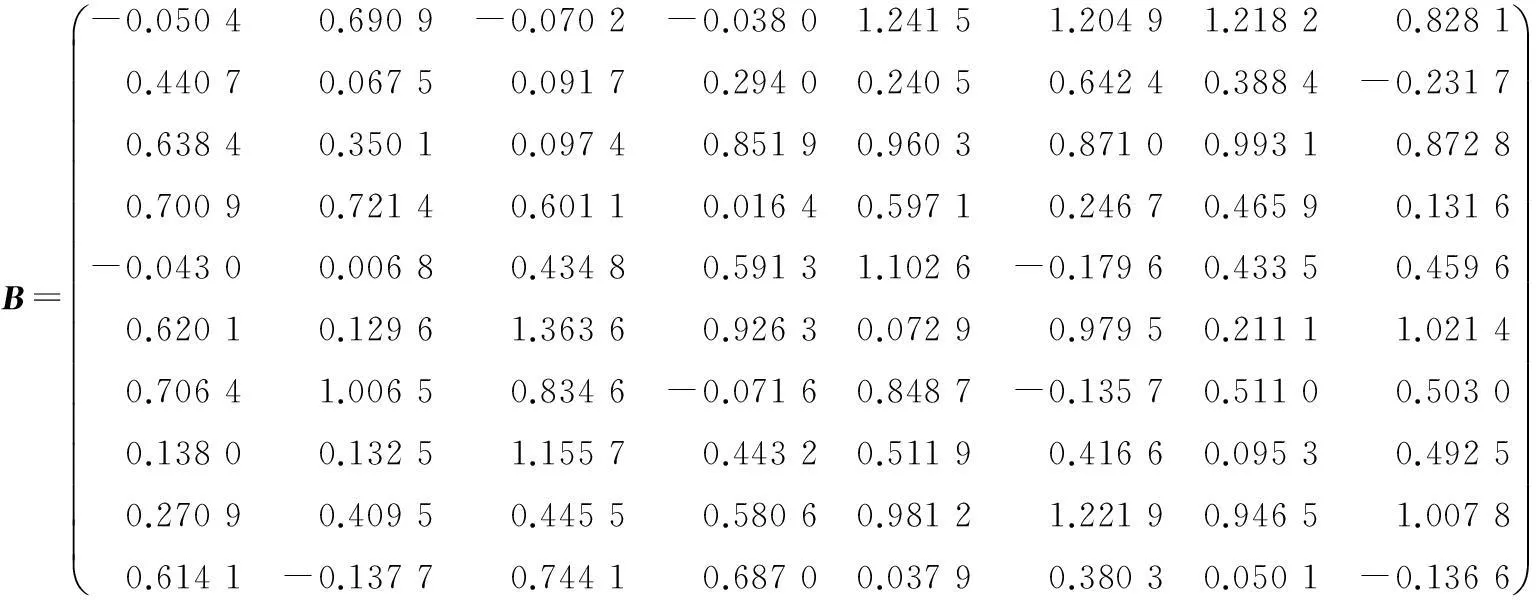
(1)求问题Ⅰ的极小范数解X*.

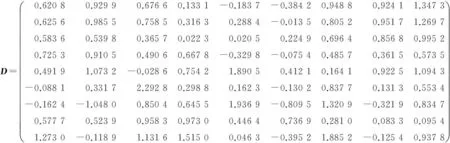
(2)若问题Ⅰ相容，给定

求问题Ⅱ的解.

下面计算结果是在Windows XP操作系统、频率2.40 GHz的计算机处理器环境下利用Matlab7.4编程给出的.

(1) 取X0=O∈R9×8作为初始矩阵，ε=5×10-10作为迭代终止的条件，即当‖ΔXk‖<ε迭代终止.对于本例可以得到问题Ⅰ的极小范数解为

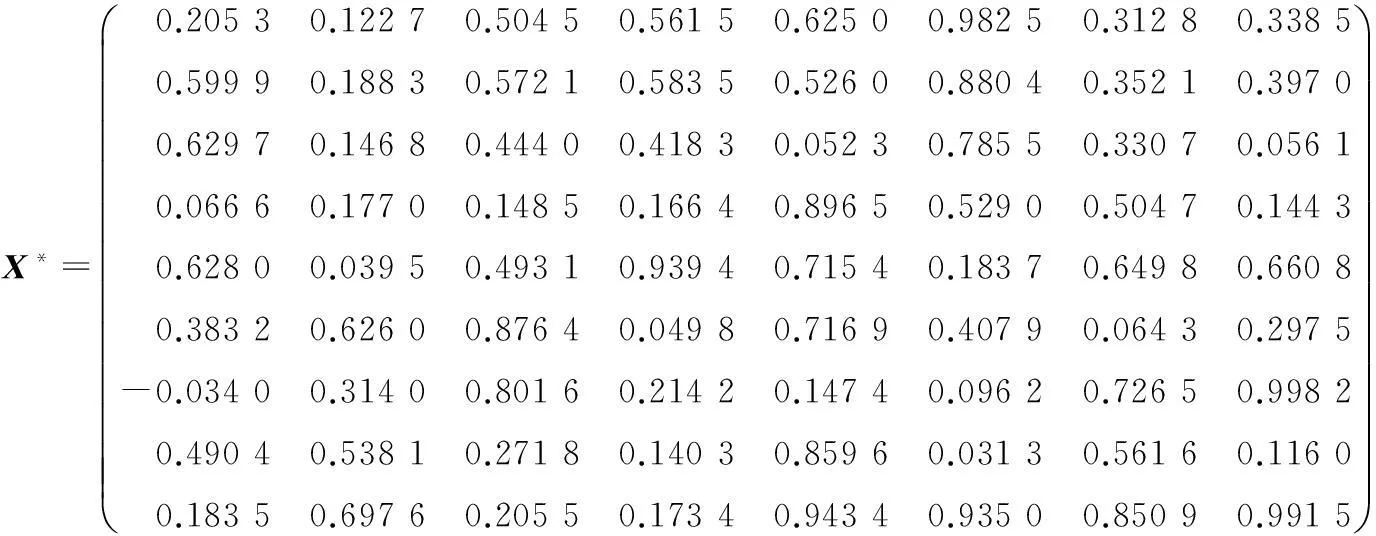
迭代过程所花的时间及迭代次数分别为t=0.030 425 s,k=108.

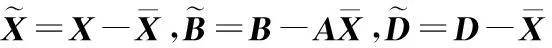
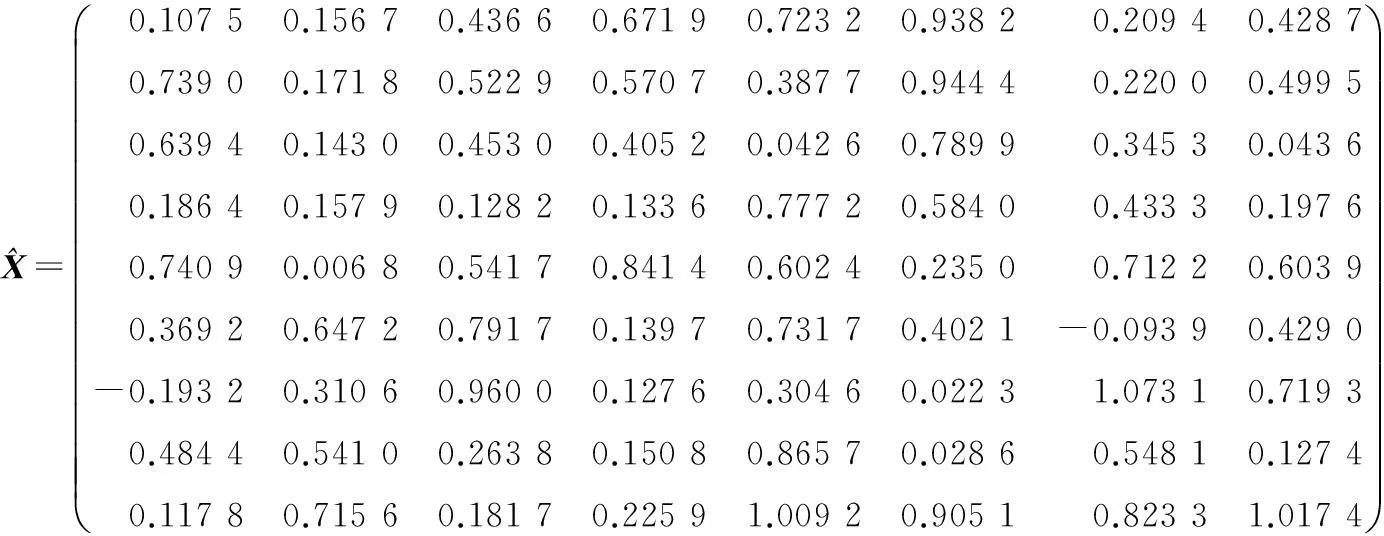
迭代过程所花的时间及迭代次数分别为t=0.035 521 s,k=87.

参考文献：

[1]BERMANA，PLEMMONSRJ.NonnegativeMatricesintheMathematicalSciences[M].NewYork:AcademicPress，1994.

[2]MITRASK.TheMatrixEquationsAX=B,XC=D[J].Linear Algebra and Its Application,1984，59：171-181.

[3] 袁永新.关于矩阵方程AX=B,XC=D及AXB=D的对称正定解[J].华东船舶工业学院学报，2000，14(6)：9-13.

[4] 陈永林.求解矩阵方程组AX=B,XC=D的迭代法[J].南京师范大学学报，1999，22(2):1-2.

[5] 李范良.几类特殊矩阵的左，右逆特征对问题及其矩阵方程组问题[D].长沙：湖南大学，2005.

[6] 彭亚新.几类特殊约束矩阵方程问题及其最佳逼近问题[D].长沙：湖南大学，2006.

[7] 汤赛，周富照.一类约束矩阵方程的迭代解法[J].吉首大学学报：自然科学版，2010,22(5)：29-34.

(责任编辑向阳洁)

An Orthogonal Projection Iteration Method for a Matrix Equations

ZHOU Fuzhao，TIAN Shiyu，YUAN Yanjie

(College of Mathematics and Computing Science,Changsha University of Science and Technology,Changsha 410004,China)

Abstract:An orthogonal projection iteration method for matrix equations AX=B,XC=D is studied.Firstly,the iterative method is constructed by using the theory of orthogonal projection and the properties of general matrix;secondly,its convergence is proved by using the singular value decomposition,the orthogonal invariance of F￣norm and the properties for solutions of the matrix equations and the estimation of its convergence rate is obtained;finally,numerical examples are given to verify the validity of the algorithm.

Key words:matrix equations;general solution;orthogonal projection iteration method;optimal approximation;minimum norm solution

作者简介：周富照(1964—)，男，湖南涟源人，长沙理工大学数学与计算科学学院教授，博士，主要从事数值代数研究.

基金项目：国家自然科学基金资助项目(11371072)

收稿日期：2014-10-31

中图分类号：O241.6

文献标志码：A

DOI:10.3969/j.cnki.jdxb.2015.03.001

文章编号：1007-2985(2015)03-0001-06