电压激励蔡氏电路混沌的解析预测及其仿真
2016-01-29
李邦彦,李连军
(湖南电气职业技术学院机械系,湖南 湘潭 411101)
电压激励蔡氏电路混沌的解析预测及其仿真

李邦彦,李连军
(湖南电气职业技术学院机械系,湖南 湘潭 411101)
摘要:蔡氏电路的非线性动力学行为丰富,其状态方程是三阶微分方程,常利用该电路研究混沌现象.首先,建立电压激励蔡氏变形电路模型;其次,运用解析方法对该电路产生混沌现象的参数取值范围进行预测;最后,采用数值方法和李雅普诺夫指数分析方法对预测结果进行仿真,验证了该电路混沌解析预测结果的正确性.
关键词:电压激励;蔡氏电路;混沌;解析预测
混沌现象是非线性动力学中一种特有的运动形式,其理论研究不仅涉及到数学、物理学、力学等,而且在化学、生物学、经济学、管理学等领域也有所研究.到目前为止,很多学者[1-4]通过各种形式的电路模型来研究混沌现象,得出了许多有用的结论.具有混沌行为的电路很多,最简单的电路是蔡氏电路,这个电路是华裔科学家蔡少棠教授1983年搭建起来的,该电路开创了用电子电路研究混沌现象的先例.后来,许多学者对蔡氏电路进行了改进,提出了各种变形蔡氏电路模型,这些电路也能产生丰富的混沌现象[5-9].蔡氏电路及其变形电路的研究方法比较多[10].笔者建立了一个电压激励蔡氏电路模型,对该电路产生混沌时参数所要满足的条件范围进行预测,并对预测结果进行仿真,验证了预测结果的正确性.
1电压激励蔡氏电路的动力学方程
研究者常采用增加电路的维数变形蔡氏,于是电路状态方程由原来的三阶变成了四阶甚至更高阶的方程.笔者设计的变形蔡氏电路是在原蔡氏电路的电感支路上串联了一个电压源(图1),此变形蔡氏电路称为电压激励蔡氏电路.由基尔霍夫电流以及电压定律可知,电压激励蔡氏电路的动力学方程为
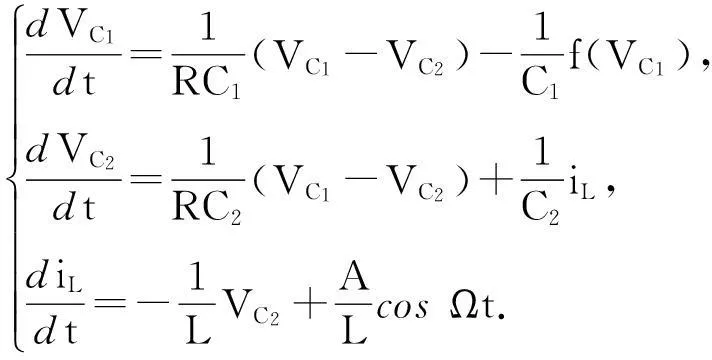
(1)
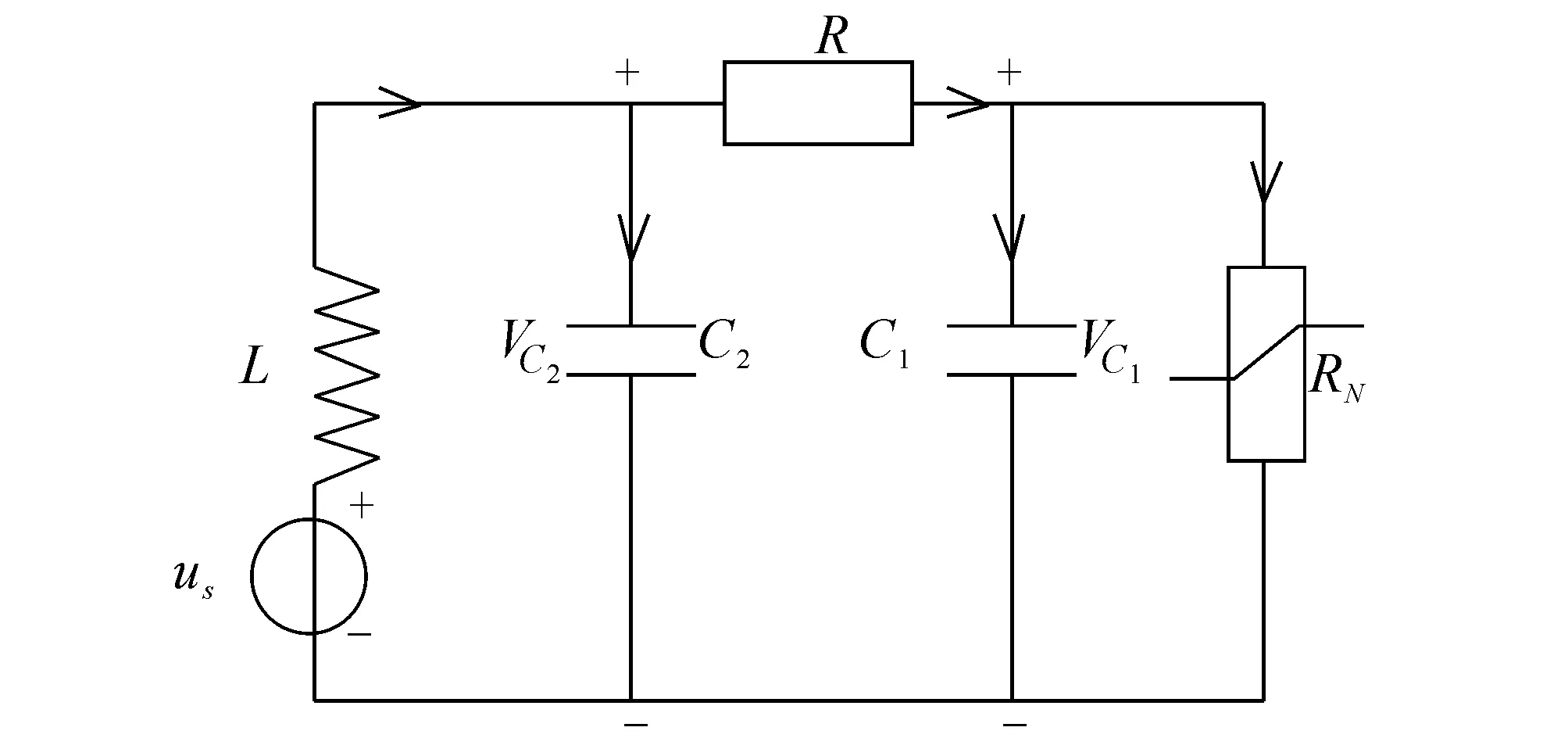
图1 电压激励蔡氏电路
其中:VC1,VC2为C1,C2的电压;iL为L的电流;f(VC1)是非线性电阻的伏安特性函数.设激励电压us=Acos(Ωt+Φ),其中A为电压源的振幅,Ω为电压源的频率,Φ为电压源的初相位.文中采用初相位为0的电压源进行研究,即Φ=0.
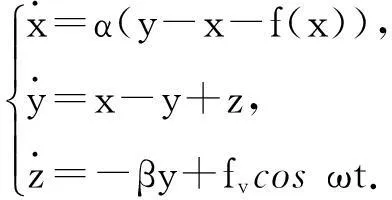
(2)

2解析预测
2.1 一次谐波解缓参数的平均化方程
由非线性动力学和混沌理论可知,若非线性项可视为弱非线性问题,且系统的振幅和初相位随时间作缓慢变化,则系统(2)的一次谐波解为z=acosωt+bsinωt,其中a和b是关于时间的慢变参数.通过平均法可求得
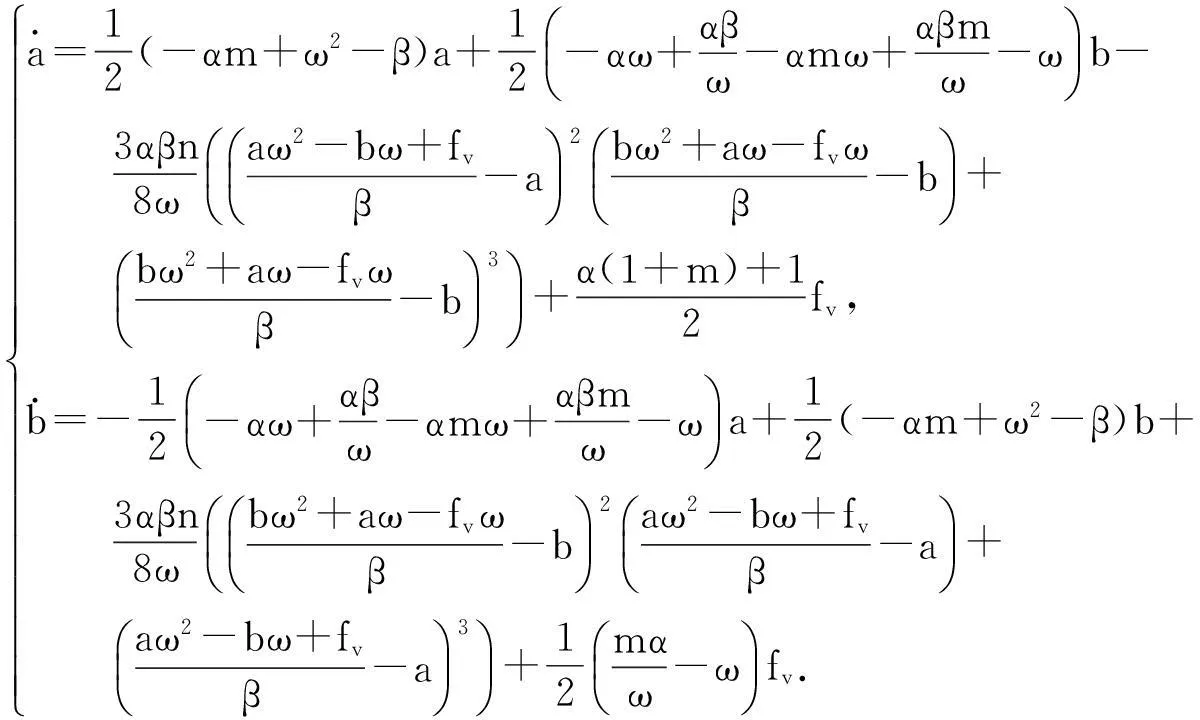
(3)
(3)式为系统一次谐波解缓参数满足的平均化方程.
2.2 一次谐波解缓参数方程的离散映射
利用a和b的慢变性质及泰勒展开式可得
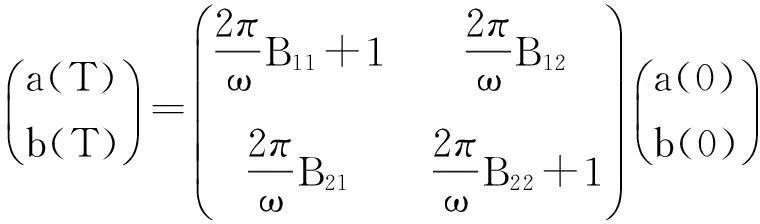
(4)
其中:
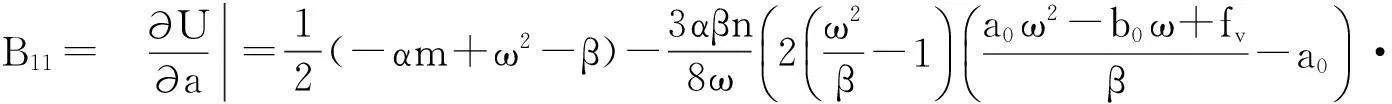
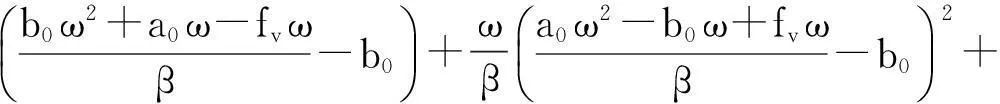
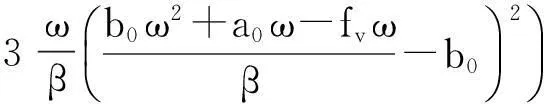



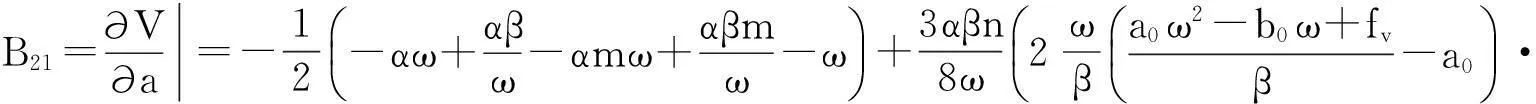
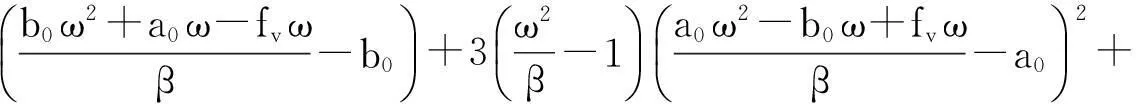

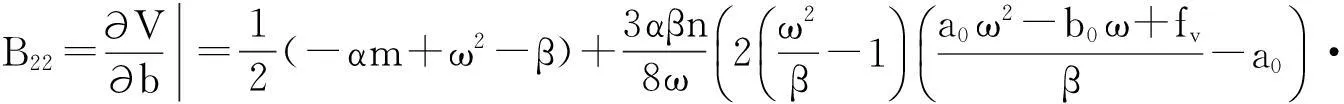
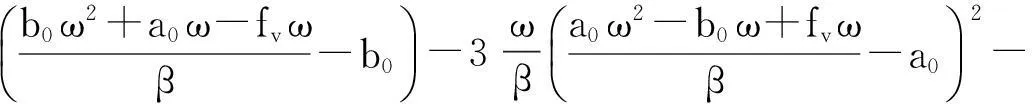
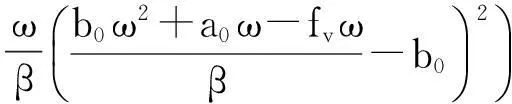
显然(4)式是系统的谐波解慢变参数平均化方程的离散映射,即
P(a(t),b(t))=TP(a(0),b(0))
(6)
的具体表达式.比较(4),(5)式可知
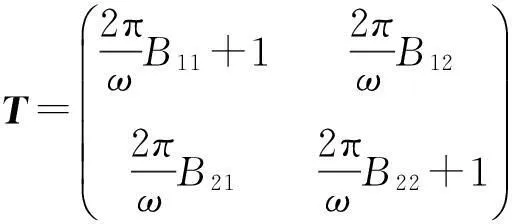
2.3 电压激励蔡氏电路产生混沌的参数条件
设T的特征值为λ,则
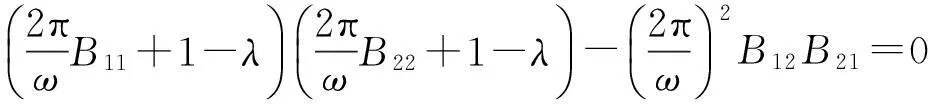
由离散动力学理论知,当λ1<1<λ2时,慢变参数一次谐波解满足的动力学方程的奇点存在鞍点,系统(2)才会出现混沌现象.因此,系统出现混沌现象的条件为
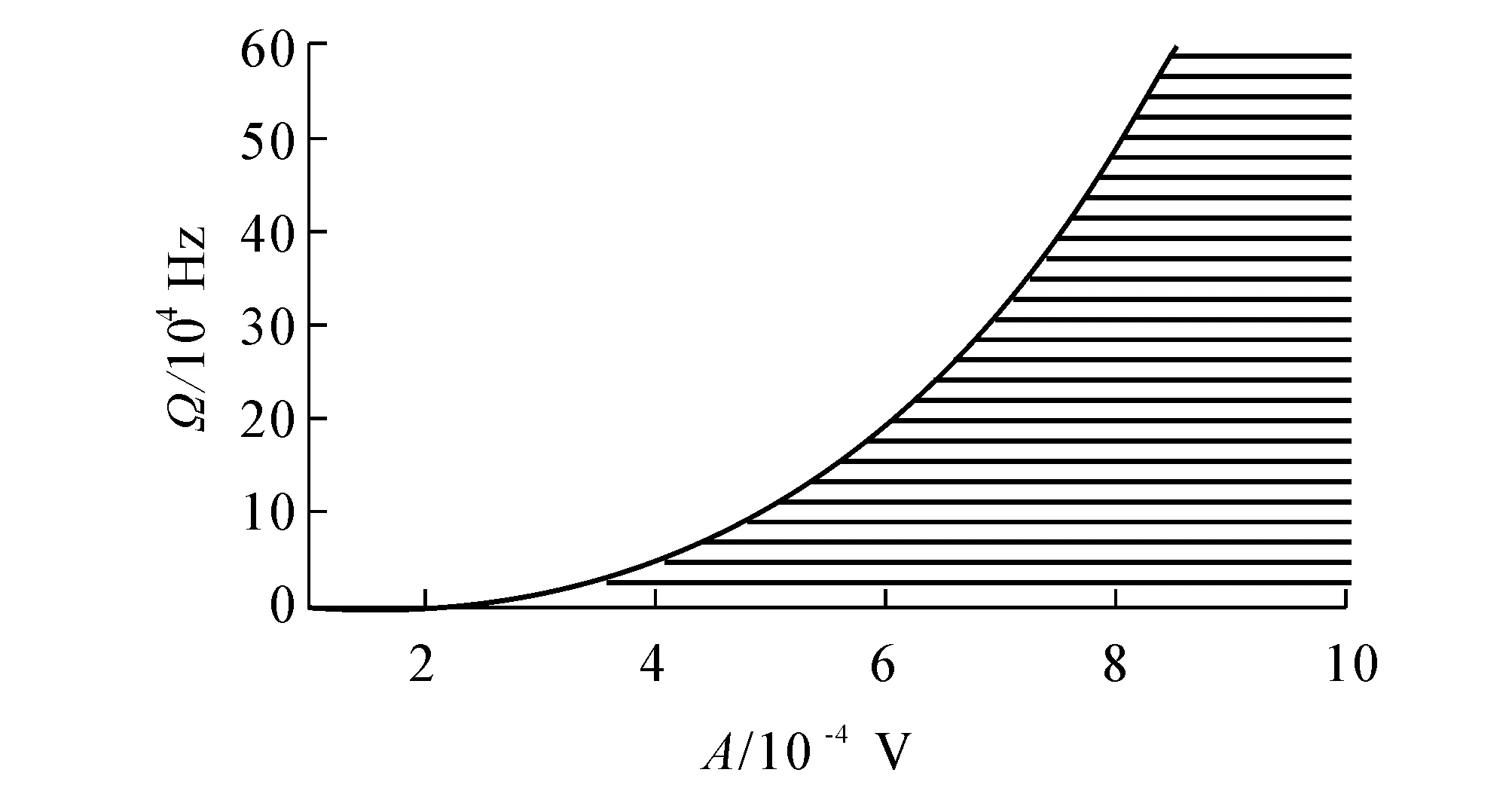
图2 解析预测结果
(6)
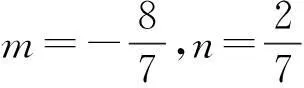
3混沌解析预测的仿真
3.1 相图仿真
(1)在预测出现混沌的范围内任取3组A与Ω值进行相图仿真,仿真结果如下:
(ⅰ)当Ω=2×104Hz,A=0.2×10-4V时,系统的相图收缩,形成奇怪吸引子,如图3(a)所示,系统呈现混沌运动的趋势.
(ⅱ) 当Ω=4×104Hz,A=1×10-4V时,系统的相图收缩,形成奇怪吸引子,如图3(b)所示,系统呈现混沌运动的趋势.
(ⅲ)当Ω=7×104Hz,A=8×10-4V时,系统的相图收缩,形成奇怪吸引子,如图3(c)所示,系统呈现混沌运动的趋势.
(2)在预测不出现混沌的范围内任取3组A与Ω值进行相图仿真,仿真结果如下:
(ⅰ)当Ω=2×104Hz,A=1×10-4V时,系统相图虽闭合,但不形成吸引子,如图3(d)所示,系统呈倍周期运动趋势.
(ⅱ)当Ω=4×104Hz,A=8×10-4V时,系统相图为1周的闭合曲线,如图3(e)所示,系统做周期运动.
(ⅲ)当Ω=7×104Hz,A=50×10-4V时,系统相图为2周的闭合曲线系统,如图3(f)所示,系统呈倍周期运动趋势.
由图3可知,仿真的结果与预测结果一致.
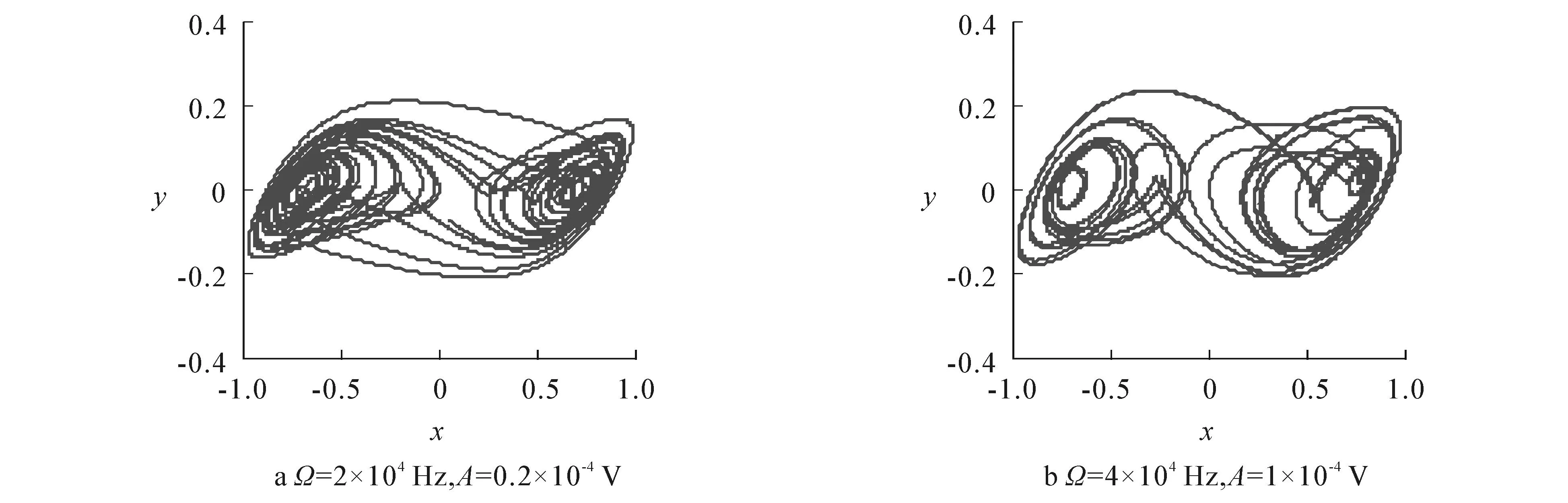
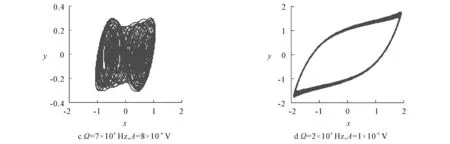
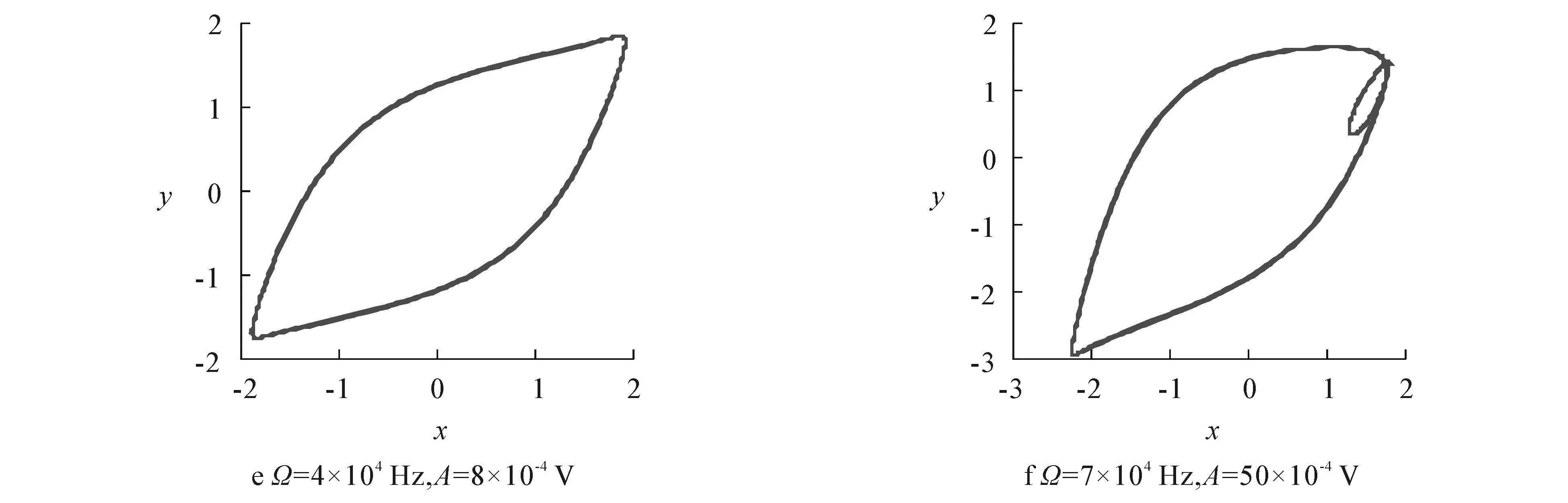
图3 仿真结果
3.2 李雅普诺夫指数计算验证
判断一个非线性系统是否存在混沌运动,需要检查它的李雅普诺夫指数λ是否有正值.利用奇异分解法与Matlab软件可得系统(2)的李雅普诺夫指数λ1,λ2,λ3,如表1所示.由表1可知,取预测出现混沌现象的3组A与Ω值,李雅普诺夫指数的3个值中1个为正,2个为负,说明系统做混沌运动,取预测不出现混沌的3组A与Ω值,李雅普诺夫指数的3个值中1个为0,2个为负,说明系统做周期或倍周期运动,与预测结果是一致.
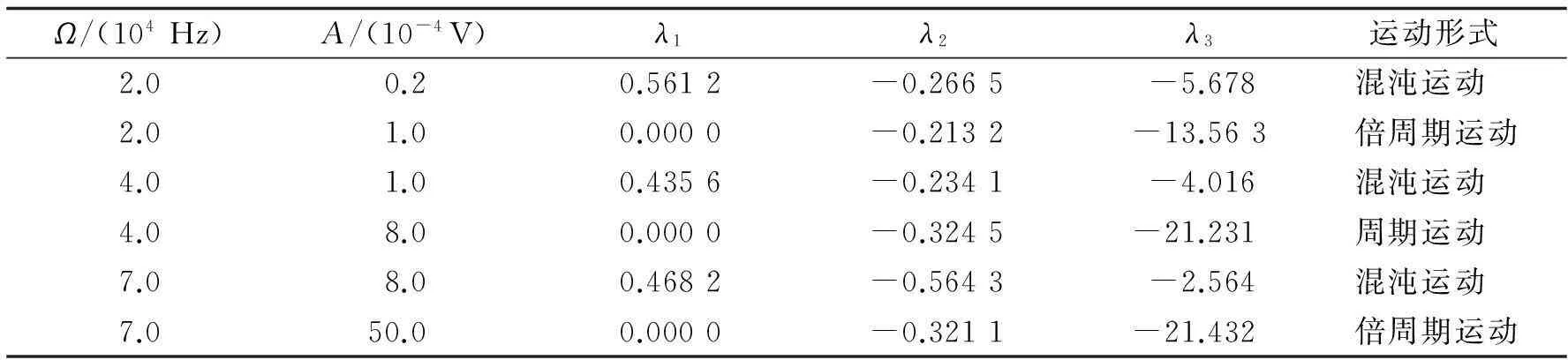
表1 李雅普诺夫指数的计算结果及运动形式
4结语
利用解析方法对电压激励蔡氏电路所对应的三阶非线性微分方程产生混沌的参数范围进行了预测,得出了电压激励蔡氏电路产生混沌的参数条件.利用数值仿真和李雅普诺夫指数分析方法对该条件进行验证,证明了混沌解析预测的正确性.在电压激励蔡氏电路中,激励电压频率高的区域比低的区域容易产生混沌,在某个频率以下的频率区域基本不产生混沌,在某个频率以上的频率区域激励电压的振幅越小越容易产生混沌.
参考文献:
[1] 王育飞,姜建国.不对称非线性蔡氏电路产生的混沌现象分析[J].系统工程与电子技术,2010,29(12):12.
[2]CUOMOKM,OPPENHEIMAV.CircuitImplementationofSynchronizedChaoswithApplicationstoCommunications[J].Phys.Rev.Lett.,2012,71:65-68.
[3]OMERO,ALIA.FlickerStudyUsingaNavelArcFurnaceModel[J].IEEETrans.onPow.Del.,2010,17(4):1 158-1 163.
[4]CHENXY,LUJF.AdaptiveSynchronizationofDifferentChaoticSystemswithFullyUnknownParameters[J].PhysicsLettersA,2012,364(2):123-128.
[5 ]LÜJ,ZHOUT,ZHANGS.ChaosSynchronizationBetweenLinearlyCoupledChaoticSystem[J].Chaos,Solitons&Fractals,2010,22(4):52-59.
[6] 冯立军,谷德桥.异结构不确定混沌系统的同步控制与参数识别[J].应用光学,2008,29(1):156-159.
[7]YANJJ,LINJS,LIAOTL.SynchronizationofaModifiedChua’sCircuitSystemviaAdaptiveSlidingModeControl[J].Chaos,Solitons&Fractals,2012,24(1):45-52.
[8]GEZM,HSUMY.ChaosExcitedChaosSynchronizationsofIntegralandFractionalOrderGeneralizedvanderPolSystem[J].Chaos,SolitonsandFractals,2011,23(3):592-604.
[9] 王光义,丘水生,许志益.一个新的三维二次混沌系统及其电路实现[J].物理学报,2006,55(7):32-35.
[10] 张朝霞,禹思敏.用时滞和阶跃序列组合生成网格多涡卷蔡氏混沌吸引子[J].物理学报,2009,58(1):121-126.
(责任编辑陈炳权)
Analytical Prediction and Simulation of Chaos in
Voltage Driven Chua’s Circuit
LI Bangyan,LI Lianjun
(Department of Mechanical Engineering,Hunan University of Electric Technology,Xiangtan 411201,Hunan China )
Abstract:Chua’s circuit can produce complex nonlinear dynamics,the state of which is three order differential equations and which is used to study chaos behavior.Firstly,a voltage driven model of Chua’s deformed circuit is set up.Secondly,an analytical method to predict the scope of the parameters of chaos of the third-order nonlinear differential equations is proposed.At last,numberical method and Lyapunov exponent analysis are used to simulate the prediction result,which verifies the correctness of chaotic prediction analysis of this circuit.
Key words:voltage driven;Chua’s circuit;chaos;analytical prediction
作者简介:李邦彦(1970—),男,湖南东安人,湖南电气职业技术学院副教授,硕士,主要从事非线性电路、非线性振动理论及其仿真研究.
基金项目:湖南省教育厅科学研究项目(11C0310)
收稿日期:2014-12-25
中图分类号:O231.2
文献标志码:B
DOI:10.3969/j.issn.1007-2985.2015.02.010
文章编号:1007-2985(2015)02-0046-06
