前置导管振动频率与强度分析

张小雅，　阎　岩

(上海船舶运输科学研究所,上海 200135)



前置导管振动频率与强度分析

张小雅，阎岩

(上海船舶运输科学研究所,上海 200135)

摘要:附连水质量的分布直接影响前置导管振动分析结果的准确性,而目前还没有针对附连水质量的精确计算公式。对此,在分析前置导管的湿模态时，分别采用公式法和流固耦合法进行计算，验证流固耦合三维数值模拟的可行性，修正公式法的系数。同时,根据不同载荷组合，对导管结构应力水平进行有限元分析校核，为相关船舶设计提供一定的依据。

关键词:前置导管；附连水质量；湿模态；干模态；流固耦合；强度有限元分析

0引言

船舶前置导管能提高螺旋桨的推进效率，减少空泡和激振，改善艉部流场。其最早提出见诸于《日本造船学会志》1982年第二期的报道。我国的相关学者也于20世纪80年代后期开始,进行了大量的试验研究[1-2]，研究成果也已被广泛应用于实船的设计与改造中[3,6]。

由于船舶艉部流场复杂，前置导管位于螺旋桨附近而使得激振力较强，因此如果设计不当，船体与导管会产生共振而遭到破坏。此外，船体摇摆和升沉引起的惯性作用力及艉部砰击载荷等都会影响导管和船体焊接处的应力水平，而国内目前鲜有前置导管模态分析和结构强度评估方面的研究。在一艘矿砂船上设置前置导管(浆前节能导管)，运用流固耦合法计算出前置导管的振动频率和振型，同时对导管和船体连接处的结构应力进行分析，以设计出合理的前置导管。

1前置导管结构介绍

共设计了两种方案下不同尺寸的前置导管，导管尺寸见表1和表2。

表1　方案一前置导管尺寸

表2　方案二前置导管尺寸

结构方面，两种方案下的导管是由横向和纵向隔板相交组成的框架与内外壳板焊接而成的,导管截面为机翼型(见图1)。

图1　导管机翼型截面图

导管內壳和外壳板厚度均为14AH36，导管内板格厚度为12AH36。方案一导管重量约为17 t，方案二导管重量约为20 t。

2干模态和湿模态分析

为能如实反映导管振动情况，建立包括整个导管和部分相接船体在内的三维有限元模型(见图2)。前置导管直接焊接在船体上，同时在水平和垂直方向设置了肘板。

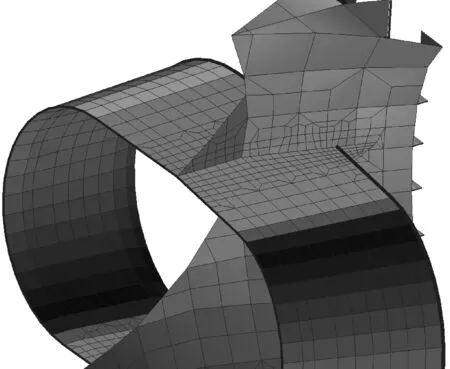
图2　前置导管有限元模型

在MSC/Nastran中，干模态和湿模态的计算都可以进行,其中湿模态的计算运用Nastran中卡片mfluid进行流固耦合分析，可准确定义不可压缩流体属性、流体密度及流固耦合作用面等。该卡片定义计算中调用了虚拟质量法，有效考虑水深对于固有模态的影响。

表3和表4列出了导管干模态和湿模态两种方案下的振型和固有频率。

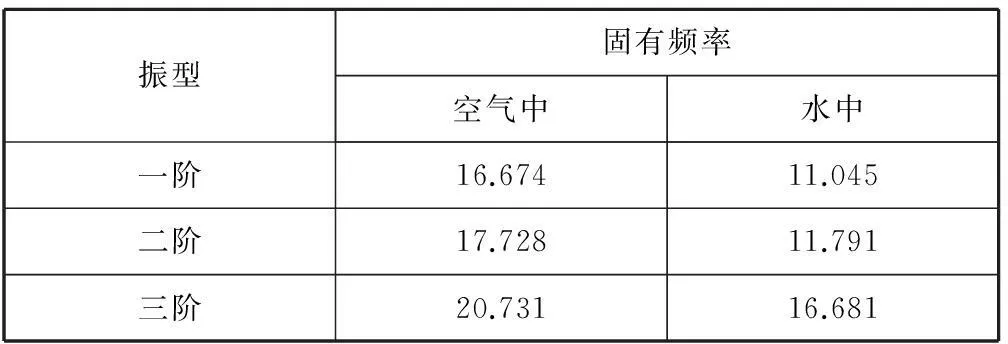
表3　方案一下的振型和固有频率　Hz

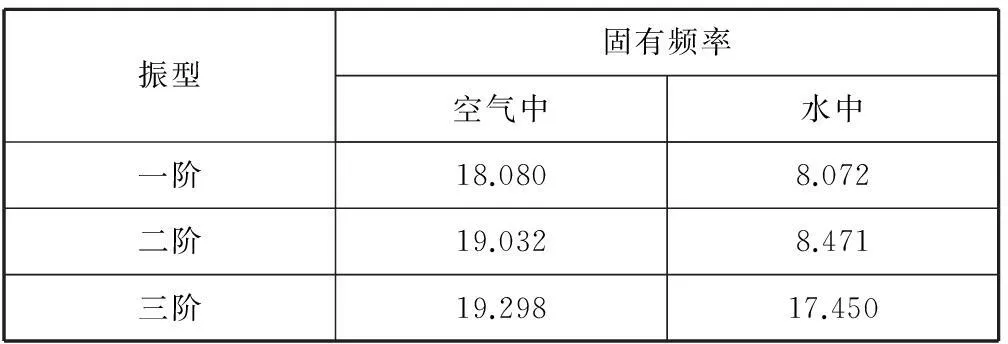
表4　方案二下的振型和固有频率　Hz

由表3和表4可以看出，同干模态振动频率相比，考虑附连水质量情况,采用流固耦合方法计算得到的湿模态振动频率较低，附连水质量对船体结构振动影响相当剧烈。在船体结构振动的研究中,附连水质量施加的准确性直接影响船体振动频率的精度。

以方案一为例，导管前三阶的典型振型见图3~图5。

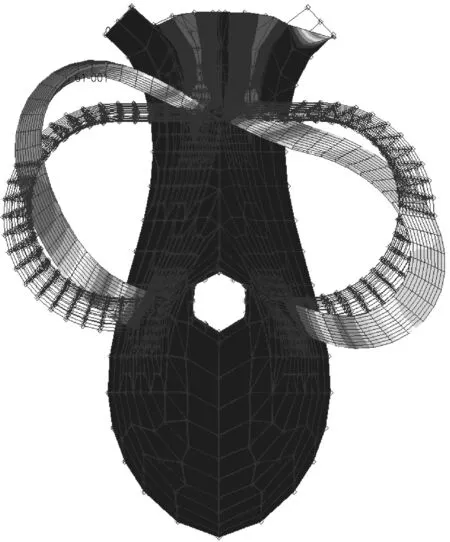
图3　导管一阶振型

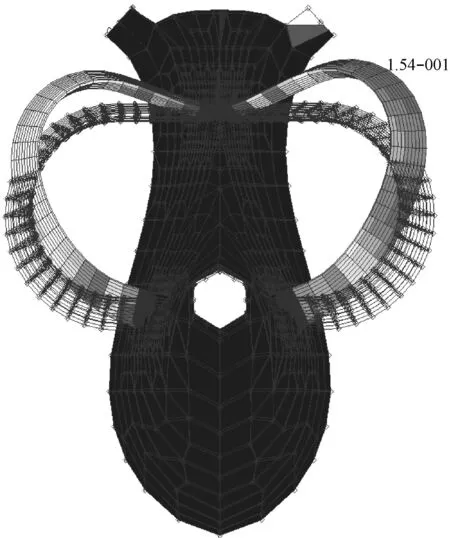
图4　导管二阶振型

图5　导管三阶振型

该船主机的常用转速为59.9 r/min，螺旋桨为4叶桨，叶频和倍叶频分别为4 Hz,8 Hz。两种方案的最小频率储备见表5。

表5　两种方案的最小频率储备

由表4可以看出:虽然方案二导管重量比方案一导管重量小，但由于方案二导管的固有频率与螺旋桨的激励频率非常接近，容易发生共振;而方案一导管的固有频率避开了螺旋桨的激振频率，有一定的频率储备，同时能有效降低导管和船体连接处的应力水平。综合考虑各种因素，前置导管设计采用了方案一。

3公式法计算与流固耦合软件计算湿模态的比较

对于单面接触液体的矩形板，单位面积上的附连水质量可按式(1)计算[7]。

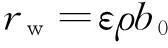
(1)

式(1)中:rw为板架单面接触水时单位面积上的附加水质量,kg/m2；b0为板架短边长度,m；ρ为水的密度,kg/m3；ε为系数。

利用公式法计算的导管附加质量约为25 t，以调节密度的方式加载到前置导管有限元模型中。湿模态计算结果见表6。

表6　用公式法计算与用流固耦合软件计算湿模态　Hz

可以看出,通过增加附连水质量对式(1)进行修正后得到的结果与利用流固耦合软件计算得到的结果较为接近，修正系数为1.6。对于单面接触液体的矩形板，单位面积上的附连水质量修正后为：

(2)

从表6中可以看出，运用流固耦合方法计算的各阶频率均低于用公式计算的船体结构振动频率。主要原因是公式法只是简单地把附连水质量以变密度的方式增加到船体质量中;而流固耦合法是在考虑船体为弹性体的基础上，通过流体与结构相互影响耦合作用，反映船体振动情况。另外，用公式法计算的附连水质量只能通过公式系数修正的方法近似计算附加质量，不能反映真实振动情况下的附连水质量分布情况。应用流固耦合方法可较为真实地模拟船体在水中振动的实际情况，并比较准确地反映附连水质量的分布，能很好地解决公式法计算的缺陷，因此应用流固耦合法能更为准确且方便地解决船体振动预报问题。

4强度分析

对前置导管进行强度评估。根据国际船级社协会(International Association of Classification Societhes,IACS)共同结构规范(Common Structural Rules,CSR)和德国劳氏船级社规范(GL Rules)等对船体载荷的要求，对前置导管在实际运营中可能受到的载荷进行定量分析。这些载荷包括船体三向运动时引起的惯性力、不同浪向下的水动力、纵摇时受到的艉部砰击载荷及回转时受到的侧向力[8]。

4.1　载荷计算

4.1.1惯性力

当船舶三向加速运动时，导管受到惯性力的作用。根据CSR对加速度的规定[9]，导管三向加速度分别为:垂向加速度av=4.19 m/s2；横向加速度at=2.7 m/s2；纵向加速度al=0.718 m/s2。

4.1.2波浪动压力

船舶在航行过程中，导管处于水线以下，受到各个方向海浪产生的动压力(见图6)。动压力的分布与水深有关，本计算是以PCL函数的形式加载到导管的内外壳表面上的。根据GLRules，波浪动压力为：

(1) 波浪方向与航行方向相同时的外部动压力Ps=10×(21.45-z)+34×2.06×(1+z/21.45);

(2) 波浪方向与航行方向垂直时的外部动压力Ps=10×(21.45-z)。

图6　动压力分布

4.1.3砰击载荷

船舶在恶劣的海况下航行时，船底会因频繁出水、入水而发生猛烈的砰击现象。由于前置导管下半部面积较大、线型较平坦，且位于艉部，因此船舶纵摇时易受到较大的砰击载荷[8]。根据中国船级社(CCS)规范[10]，对高管受到的砰击载荷进行计算。

P=0.5ρV2CdCsCp

(3)

式(3)中：ρ为海水密度；V为海水越过艏甲板的速度；Cd为外形系数；Cs为砰击系数；Cp为保护系数。经计算，艉部砰击载荷为p=234.4 kN/m2。

导管入水且横向入水角>45°时，由于水流能迅速散开，基本不受砰击载荷的影响。为此,主要考虑导管横向入水角<45°时受到砰击载荷的作用[8]。为简化计算，假设导管受到的砰击压力是均匀分布的，并将该区域计算得到的最大压力作用在导管的外壳表面上(见图7)。

图7　砰击载荷分布

4.1.4侧向推力

导管具有机翼型剖面，在水流经过时，其表面会受到垂直于来流方向升力的作用。船舶航行时，水流流向往往与航行方向不一致，特别是在转舵操作时，水流会对船舶产生横流作用。横流作用会增大进流与导管剖面的夹角，增大侧向推力[8]。

图8　侧向推力分布

导管剖面翼形的升力产生原理与舵力的产生原理相同，这里参考舵力计算的方法来评估导管侧向推力。乔赛尔公式[11]是最常用的计算剖面升力的公式，它忽略船体及螺旋桨的影响，偏于安全[8]。乔塞尔公式为

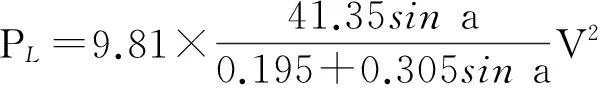
(4)

式(4)中:PL为侧向推力，N；v为来流速度；a为与来流最大夹角。经计算，导管侧向推力PL=25.2 kN/m2。

4.2　有限元法分析

建立前置导管三维有限元模型，根据不同的载荷组合对导管结构应力进行有限元分析校核。按“4.1”中估算的载荷数值和图6～图8所示的加载方式进行加载,分别为：

(1) LD1，即惯性力+波浪方向与航行方向相同时的波浪动压力;

(2) LD2，即惯性力+波浪方向与航行方向垂直时的波浪动压力;

(3) LD3，即惯性力+砰击载荷;

(4) LD4，即惯性力+导管侧向推力。

有限元计算结果见表7。由应力分析结果可知，导管结构各部分应力均满足许用应力要求。对导管结构强度影响较大的是艉部砰击载荷和波浪动压力，水流侧向压力对导管结构强度的影响很小。导管的最大应力出现在导管与船体的下端相接处。以LD3为例，其见应力云图和变形图见图9~图12。

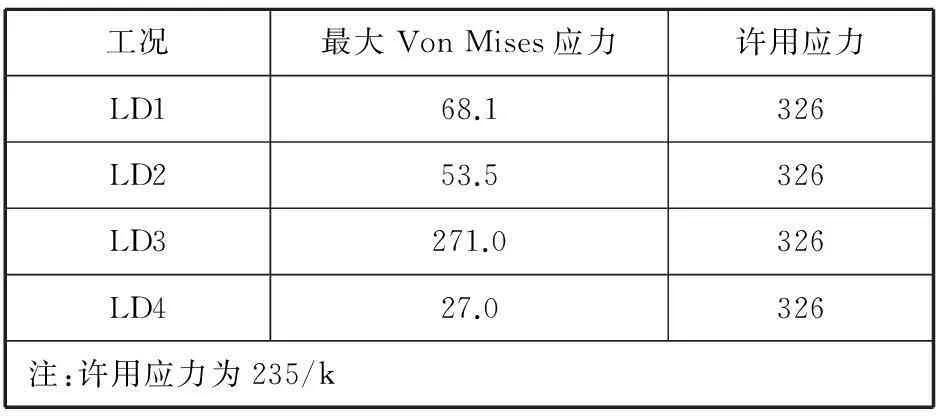
表7　四种工况下的应力值　N/mm2

图9　LD3工况导管外壳Von Mises应力

图10　LD3工况导管内壳Von Mises应力

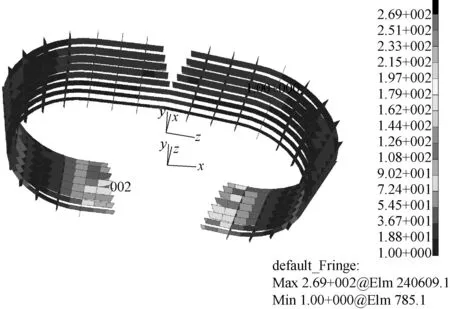
图11　LD3工况导管内板格Von Mises应力

图12　LD3工况变形图

5结语

对一艘矿砂船艉部前置导管进行了湿模态、干模态分析和有限元强度校核,验证了利用流固耦合软件计算湿模态的可行性，对公式法计算附连水质量进行了修正;同时,找到了合理的导管设计方案，避免了共振的发生。结构强度的有限元校核保证了导管结构的安全性，为以后设计前置导管提供了一定的理论依据。

参考文献：

[1]张大有.关于前置导管两个主要参数的研究[J]. 武汉水运工程学院学报, 1989, 13(3):100-103.

[2]杨怀蜀. 高效节能导管装置——舵球前置导管组合体简介[J]. 上海船舶运输科学研究所学报, 1990, 13(1): 90-91.

[3]李洁雅, 余灵, 羊少刚, 等. 货船进流补偿导管试验研究[J]. 船舶工程, 1996(3):18-20.

[4]周占群, 胡平, 刘兴威, 等. 2 800吨多用途船船型开发研究[J]. 上海船舶运输科学研究所学报, 1998, 21(1): 1-8.

[5]胡平, 周占群. 肥大型船满、压载状态下尾部伴流场的分析与探讨[J]. 上海船舶运输科学研究所学报, 1999, 22(2): 71-81.

[6]欧礼坚, 李洁雅, 王志勇, 等. 补偿导流管技术应用于双艉鳍船型的研究[J]. 华南理工大学学报：自然科学版, 2000, 28(6): 49-52.

[7]金咸定, 夏利娟. 船体振动学[M]. 上海: 上海交通大学出版社, 2011： 182-183.

[8]刘奕谦, 谢小龙. VLCC前置导管结构设计与强度分析[J]. 中国造船, 2013, 54(4):109-118.

[9]Common structure rules for double gull oil tankers [S].

[10]中国船级社. 散货船结构强度直接计算指南[S].

[11]陈可越.船舶设计实用手册(舾装分册)[M]. 北京: 国防工业出版社, 2002.

The Vibration Frequency of Flow Straightening Duct and its Strength Analysis

ZhangXiaoya，YanYan

(State Key Laboratory of Navigation and Safety Technology，Shanghai Ship & Shipping Research Institute，

Shanghai 200135，China)

Abstract:The vibration frequency of a flow straightening duct is strongly dependent on the distribution of entrained water, but the calculation of the additional mass of entrained water has not been precisely formulated. This paper analyzes the flow straightening duct in wet mode by means of the figure and the fluid-structure coupling method separately. The simulation based on the fluid-structure coupling method is verified. The coefficients of the figure are corrected. The stress of flow straightening duct installation under different load conditions is calculated with finite element analysis.

Key words:the flow straightening duct; additional mass of entrained water ; wet mode; dry mode; fluid-structure coupling; finite element analysis

中图分类号：U664.3

文献标志码：A

文章编号：1674-5949(2015)04-014-06

作者简介：张小雅(1986—),女,上海人，从事船舶与海洋结构物设计制造研究。

收稿日期：2015-07-15