叶梢与内壁间隙对导管螺旋桨水动力性能的影响

张文璨,　董国祥,　陈伟民,　任海奎

(上海船舶运输科学研究所 航运技术与安全国家重点实验室， 上海 200135)



叶梢与内壁间隙对导管螺旋桨水动力性能的影响

张文璨,董国祥,陈伟民,任海奎

(上海船舶运输科学研究所 航运技术与安全国家重点实验室， 上海 200135)

摘要:采用求解RANS方程的方法，运用计算流体力学(CFD)软件Fluent，对荷兰船模试验池推荐的No.19A+Ka4-7010导管螺旋桨模型(P/D=1.0)的敞水粘性流场进行CFD数值模拟，并分析结果得到该导管螺旋桨模型敞水状态下的水动力性能曲线。分别计算3种不同叶梢间隙(Δ=1 mm,2 mm,3 mm)下导管螺旋桨的水动力性能，研究叶梢间隙对导管螺旋桨水动力性能的影响。将Δ=1 mm工况下的计算结果与上海船舶运输科学研究所导管螺旋桨常规推进敞水试验的结果进行比较，验证该计算策略的正确性。计算结果表明：导管螺旋桨的推力、扭矩以及推进效率均随叶梢间隙的减小而增大。

关键词:导管螺旋桨； 叶梢间隙； 计算流体力学； 水动力性能

0引言

导管螺旋桨又称套筒螺旋桨，其外围有一个环形套筒，是目前较为流行的一种特殊推进器。对导管螺旋桨的研究工作约始于20世纪30年代，以MARIN的研究最为深入。其对导管形状和螺旋桨类型做了大量深入而细致的研究，在此基础上设计了No.19A+Ka系列和No.37+Ka系列导管螺旋桨。并将No.19A导管分别置于Ka3-65、Ka4-55、Ka4-70、Ka5-75螺旋桨中进行了导管螺旋桨的敞水试验[1-4]，其中Ka4-70螺旋桨选定的盘面比分别为0.6，0.8，1.0，1.2，1.4。国内方面，上海交通大学开发出了JD75+Ka4-70系列和JD7704+Ka4-70系列简易导管螺旋桨，中国船舶科学研究中心研制出了BD导管+D型螺旋桨系列的双体导管螺旋桨。多年的实践表明，导管螺旋桨具有很多明显的优点，如：可以改善重载螺旋桨的效率，可发挥导管对螺旋桨的保护作用，能够改善船舶的航向稳定性等。基于这些优点，导管螺旋桨首先在拖船、顶推船、渔船等螺旋桨载荷较重的船舶上得到了广泛应用。随着近些年船舶(特别是民用船只)逐渐向大型化、高功率方向发展，螺旋桨的载荷不断加重，很多民船也开始采用导管螺旋桨作为推进装置[5-7]。

导管螺旋桨中导管内壁与螺旋桨叶梢之间间隙称为叶梢间隙，其作为1个重要的参数，直接影响着导管螺旋桨的各项水动力性能。因此，合理选取叶梢间隙的大小对提高导管螺旋桨的水动力性能及其流场模拟精确度而言至关重要。近年来，随着电子计算机性能取得长足进步，计算流体力学(Computational Fluid Dynamics, CFD)作为流体力学的一个重要分支，得到了飞跃性的发展。CFD方法具备成本低、耗时短、假设限制少、应用范围广、获得流场数据比较容易等试验测量方法和理论分析方法都不具备的优点。因此，利用CFD数值模拟方法，以MARIN设计的No.19A+Ka4-7010(即螺距比为1.0)导管螺旋桨模型为研究对象，对不同叶梢间隙(Δ=1 mm，2 mm，3 mm)下导管螺旋桨周围的粘性流场进行数值模拟，并分析流场的特性，得出导管螺旋桨水动力性能随叶梢间隙的变化规律。

1CFD计算模型与计算策略

1.1　计算模型

1.1.1导管螺旋桨三维模型

No.19A+Ka4-7010导管螺旋桨模型对应的No.19A导管的剖面形状见图1，切面沿轴向的位置以横坐标x与导管长度l的比值表示，外表面和内表面的坐标分别用yl，yu与l的比值表示。

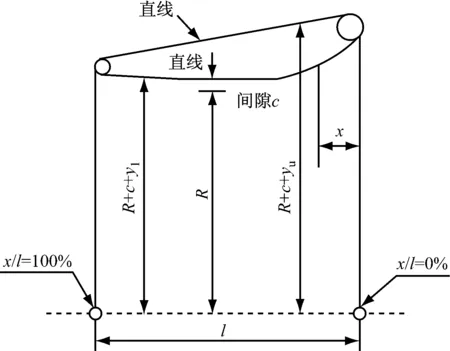
图1　No.19A导管剖面图

Ka系列螺旋桨是等螺距螺旋桨，其外部轮廓为宽叶梢的扇形轮廓，根部切面为机翼型，梢部切面为弓型。这里所研究的Ka4-7010螺旋桨模型的参数见表1。

表1　Ka4-7010螺旋桨模型参数

利用Fluent前处理软件Gambit建立No.19A+Ka4-7010导管螺旋桨的几何模型(见图2)，具体步骤为：

图2　No.19A+Ka4-7010导管螺旋桨几何模型

(1) 将螺旋桨二维几何数值经过坐标转化得到螺旋桨三维空间坐标点，并将三维空间坐标点文件导入Gambit；

(2) 遵循“由点生线、由线生面、由面生体”的原则生成螺旋桨实体；

(3) 将导管型值输入Gambit，遵循相同的原则生成导管实体。

1.1.2计算域及网格划分

计算域是与导管螺旋桨同轴的圆柱体，高度为螺旋桨直径的30倍，直径为螺旋桨直径的10倍。其中：速度入口距离推进器约7倍螺旋桨直径；压力出口距离推进器约20倍螺旋桨直径。核心计算域是半径为螺旋桨直径的2倍、高度为螺旋桨直径的3倍的与导管螺旋桨同轴的圆柱体(见图3)。

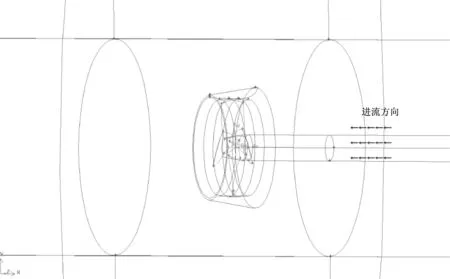
图3　核心计算域划分示意图

网格划分是指对计算区域进行离散化，即将空间上连续的计算区域划分为多个子区域，并确定每个区域中的节点。划分网格的本质是用有限个离散的点代替原来的连续空间。数学上，生成网格后(离散化后)连续的控制方程将被离散化，描写流动与传热的偏微分方程将转化为各个节点上的代数方程组[8]。网格划分是CFD模拟过程中最重要的环节，直接影响到模拟的精度和效率。如若网格过疏，则模拟精度不高；若网格过密，则又会导致计算量增大及计算难以收敛。

为便于网格划分，需要将无限流域流场空间划分为多个小空间。计算空间域被分为外部计算域、过渡区和螺旋桨计算域等三部分。

(1) 最外层为外部计算域，该区域中压力和速度分布变化并不剧烈，主要反映螺旋桨的来流和尾流情况，因此可划分较粗的网格。

(2) 在外部计算域和螺旋桨计算域的过渡区中包含有导管表面，因此需要加入细化区，通过细化的网格合理反映导管的线型。

(3) 在螺旋桨计算域中，速度压力分布变化非常剧烈，应采用细致的网格进行计算。

在这3个区域中，外部计算域与过渡区均为静态域，而螺旋桨计算域作为旋转域，采用多重旋转坐标系(MRF)模型，设置为绕x轴以角速度行旋转，角速度为21 r/s。

内部计算域网格划分结果见图4，其网格总数为116.6万。为了更好地进行数据交换，对定义的前后interface面均采用规则划分。在进口边界处设置为速度进口条件，给定均匀来流的各速度分量；出口边界定义为压力出口边界；外部计算域圆柱体表面设为对称边界；所有壁面均设为无滑移固壁条件。

图4　内部计算域网格划分示意图

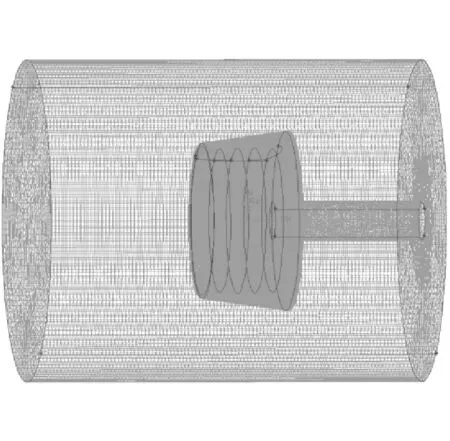
图5　过渡区计算域网格划分示意图

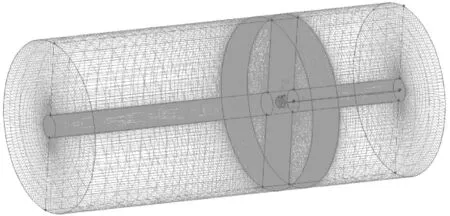
图6　外部计算域网格划分示意图1.2　计算策略

1.2.1计算流体力学基本方程

计算流体力学基本方程建立在物理守恒定律(包含质量守恒定律、动量守恒定律以及能量守恒定律)的基础之上，并由此得到流体力学连续性方程、动量方程和能量方程[9]。导管螺旋桨周围的流场为复杂、不可压缩的粘性湍流流场，而导管螺旋桨桨叶的的转动相对于导管的旋转运动可视为不可压缩流体的三维非定常流动。由于导管螺旋桨周围的流场具有不可压缩的特性，热交换很小可忽略不计，因此无需建立能量方程。

连续性方程和动量方程分别为

(1)

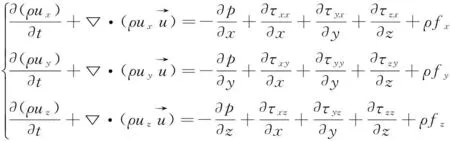
(2)

1.2.2湍流模型

Fluent包含单方程模型、双方程模型、k-ε模型、雷诺应力模型、大涡模型等多种湍流计算模型，其中k-ε模型为双方程模型，是目前使用最为广泛的湍流模型，可分为标准k-ε模型、RNGk-ε模型以及Realizablek-ε模型等[10]。

RNGk-ε模型来源于严格的统计技术，与标准模型很相似。但是，标准k-ε模型是一个高雷诺数模型，而RNG理论提供了1个考虑低雷诺数流动粘性的解析公式，这使得RNGk-ε模型在处理近壁区域低雷诺数流动时相较标准k-ε模型更具优势。此外，由于RNGk-ε模型考虑了湍流旋涡，修正了湍动粘度，考虑了平均流动中的旋转和旋流流动情况，能够更好地处理高应变率及流线弯曲程度较大的流动，因此更适合高速旋转导管桨这种复杂流动的过程。总的来说，RNGk-ε湍流模型在复杂剪切流动、含高剪切率的流动、旋流和分离流场中的预测精度要高于标准k-ε湍流模型。

根据所模拟的流场的特性，决定采用RNGk-ε双方程模型计算非定常湍流，其形式为：

(3)

(4)

1.2.3计算参数设置

计算方法采用SIMPLE半隐式连接压力方程计算方法；梯度插值方案采用Green-Gauss Cell Based方案；压力插值格式采用PRESTO!格式；动量、湍流动能以及湍流耗散度的离散格式,均选用二阶迎风差分格式。

2计算及数据分析

2.1　不同叶梢间隙下导管螺旋桨水动力性能的计算

分别取叶梢间隙Δ=1 mm,2 mm,3 mm，运用CFD软件Fluent计算出不同进速系数条件下导管螺旋桨模型的水动力性能，如:螺旋桨推力T桨,导管推力T导,螺旋桨扭矩Q导。将以上结果无因次化，得到各项水动力性能系数，如:螺旋桨推力系数KT_p,导管推力系数KT_d,推进单元推力系数KT_u,螺旋桨扭矩系数KQ以及敞水效率η0_u。水动力性能系数计算公式为

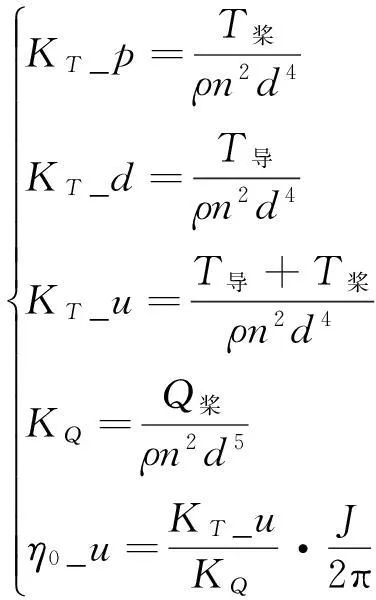
(5)

式(5)中：n为螺旋桨转速；d为螺旋桨模型半径；J为进速系数；Q为螺旋桨扭矩；TP为螺旋桨推力；TN为导管推力。

2.2　叶梢间隙时导管螺旋桨的水动力性能的影响分析

依据计算结果，绘制出导管螺旋桨水动力性能系数的变化曲线见图7。

图7　不同叶梢间隙下导管螺旋桨水动力性能参数变化曲线图

从以上导管螺旋桨水动力性能系数曲线可以看出，螺旋桨推力系数、导管推力系数、推进单元推力系数、螺旋桨扭矩系数以及敞水效率均随着叶梢间隙减小而增大。且当叶梢间隙取1mm时,计算值与试验值相比较而言更为接近。

以进速系数J=0.4时的工况为例，对导管螺旋桨桨叶表面的压力分布情况、导管壁压力分布情况以及螺旋桨盘面的速度分布进行分析。

图8-图10显示叶梢间隙分别为1 mm,2 mm,3 mm时导管螺旋桨叶背以及叶面的压力分布情况。可以看出，在叶背(吸力面)上，叶梢处吸力达到最大值，从叶梢到叶根，吸力不断减小；导边以及随边处吸力达到最小值，从导边到随边，吸力先是增大，接着降低。在叶面(压力面)上，导边处压力达到最大值，导边及随边处为高压区；叶梢处压力达到最小值；其它部分压力分布较为均匀。将图8、图9、图10对比可知，随着叶梢间隙的增大，叶背上的高吸力区部分面积、叶面上的高压区部分面积均逐渐减小，则螺旋桨推力减小。这印证了计算结果。

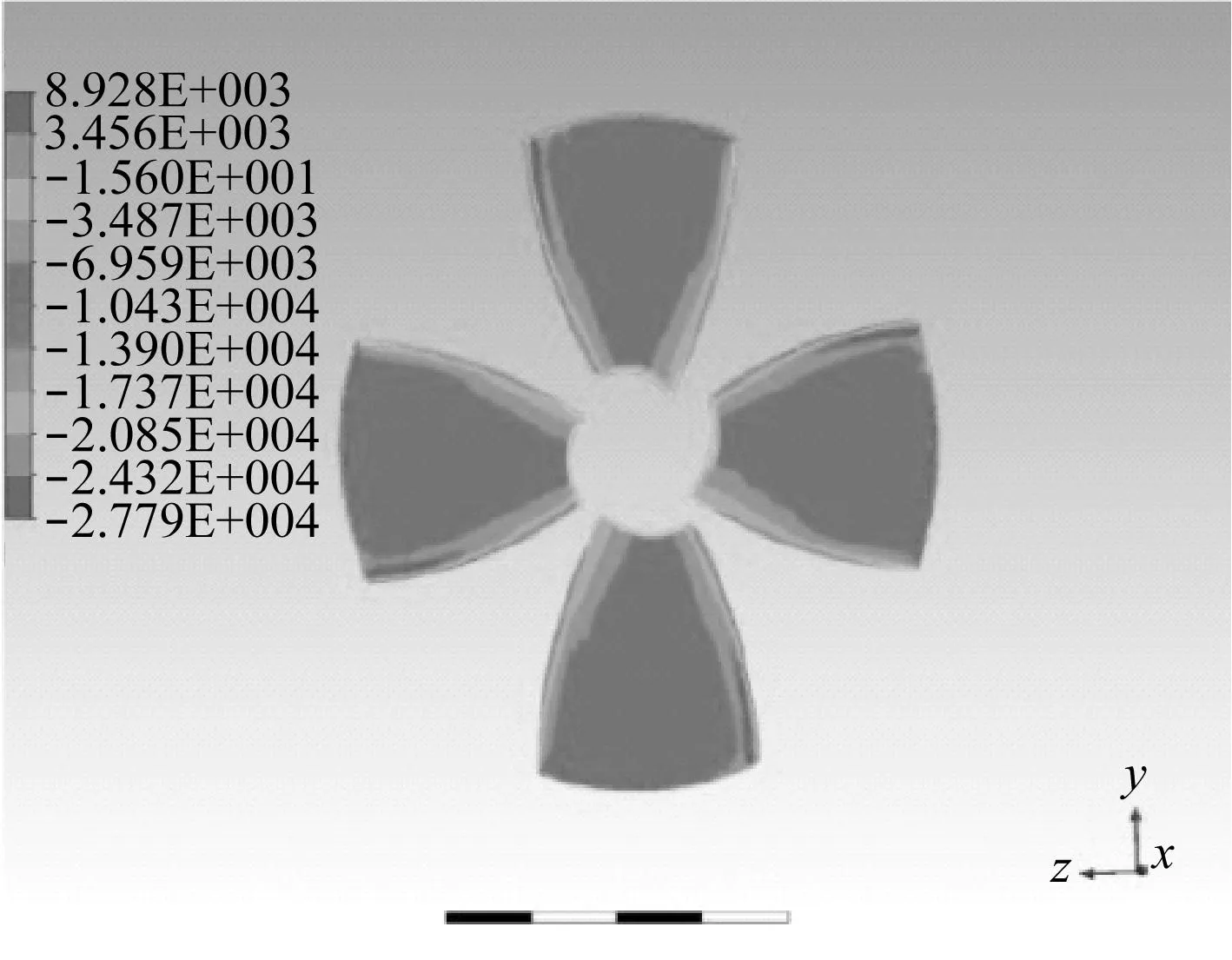
(a) 叶背压力分布图

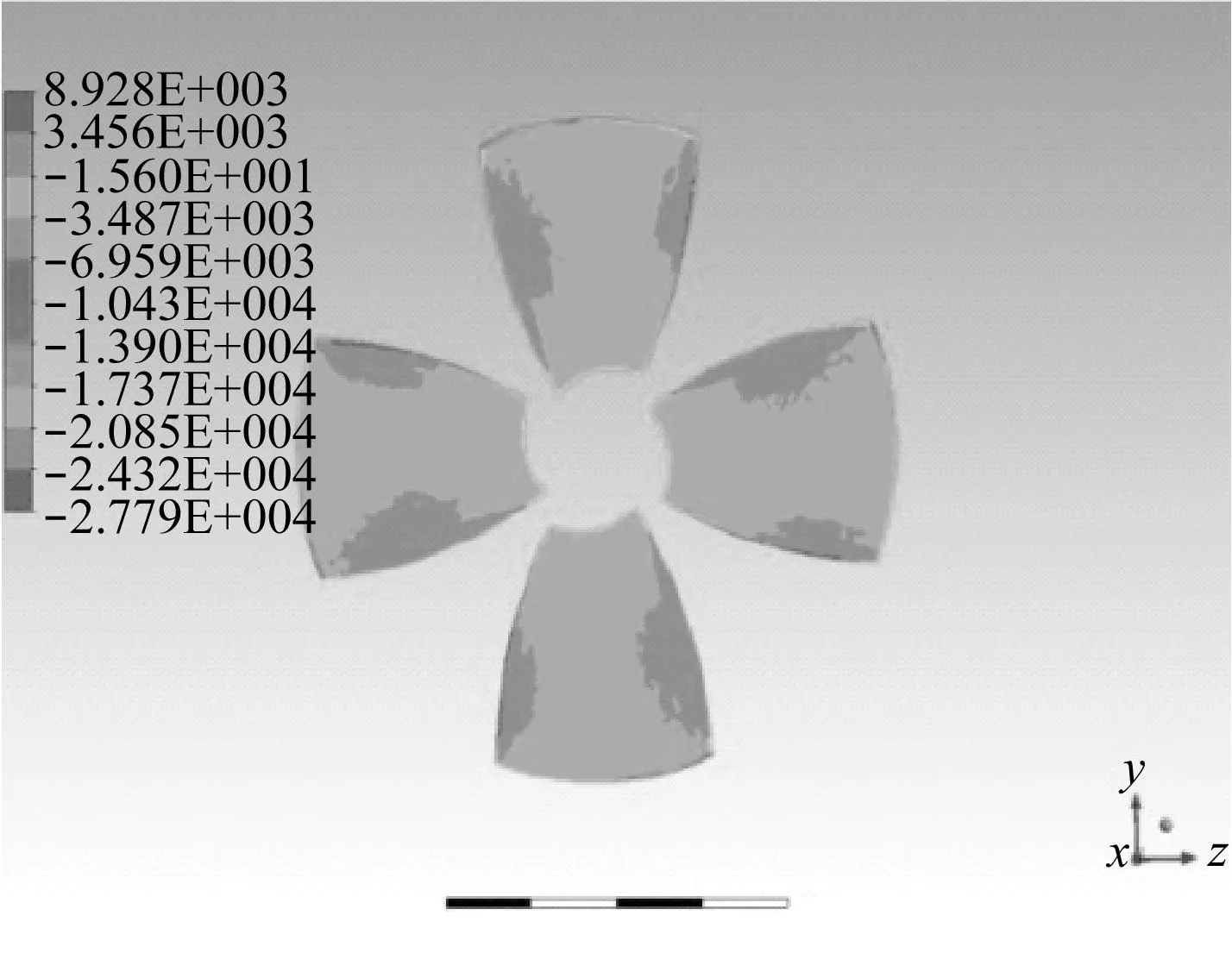
(b) 叶面压力分布图

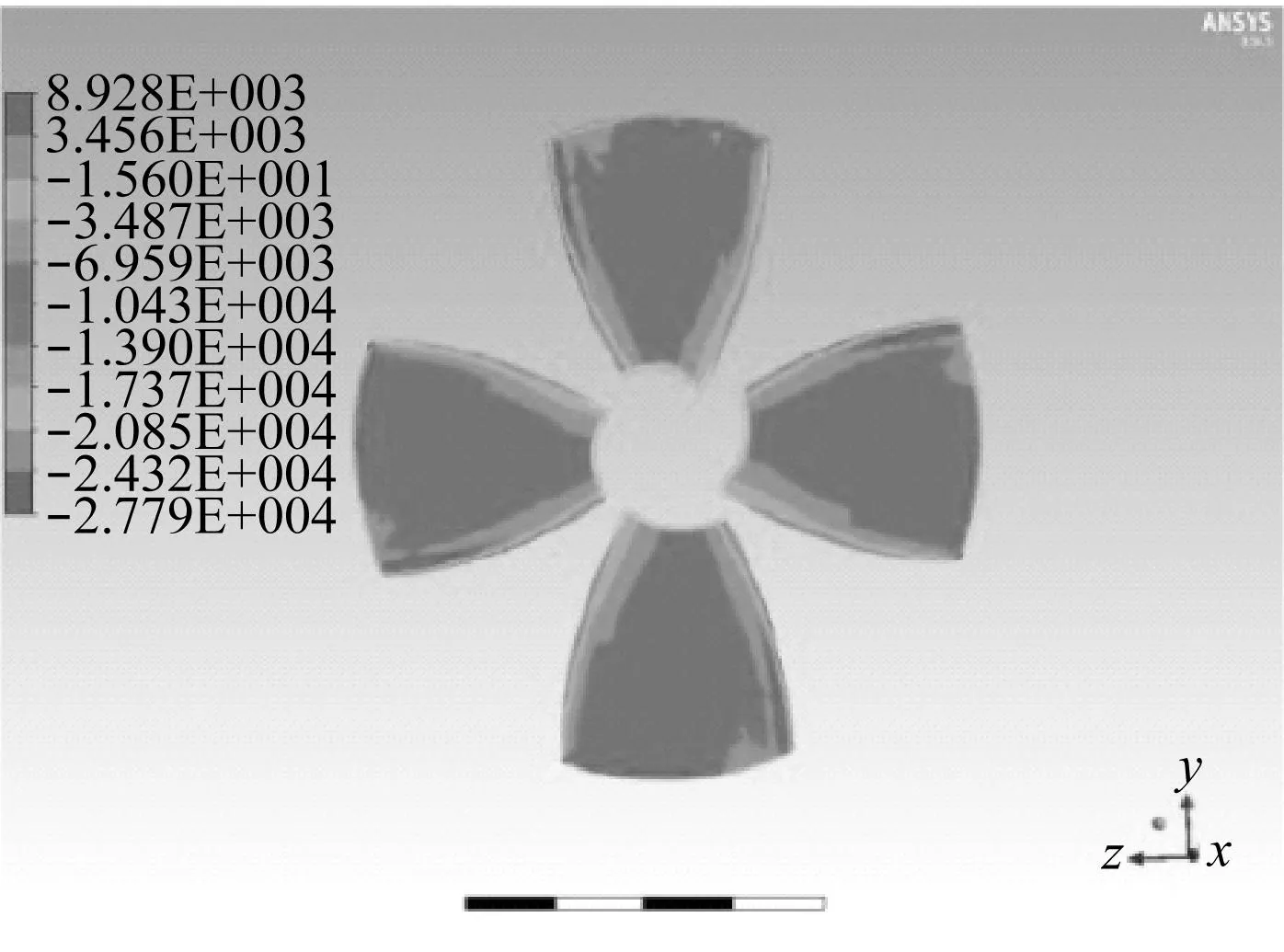
(a) 叶背压力分布图

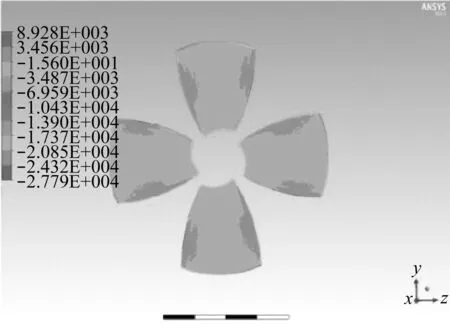
(b) 叶面压力分布图

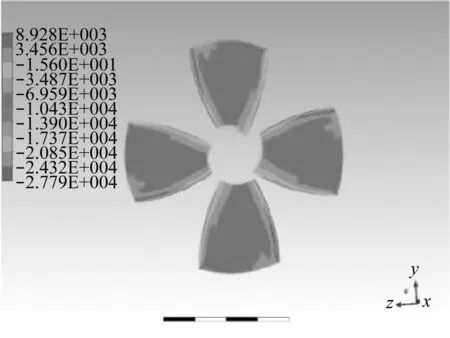
(a) 叶背压力分布图

(b) 叶面压力分布图

图11显示叶梢间隙分别为1 mm,2 mm、3 mm时导管壁压力分布。其中左上为1 mm，右上为2 mm，下方所示为3 mm。导管外壁为高压区，压力分布均匀；导管内壁为低压区，且在靠近螺旋桨处压力最低。将三幅图对比可知，随着叶梢间隙的增大，导管外壁的压力变化不明显，而导管内壁低压区的面积不断减小，则导管外壁与内壁的压力差减小，其在x轴方向上的分量减小,故随着叶梢间隙增大，导管推力减小。

(a) 叶梢间隙为1 mm时导管壁压力分布

(b) 叶梢间隙为2 mm时导管壁压力分布

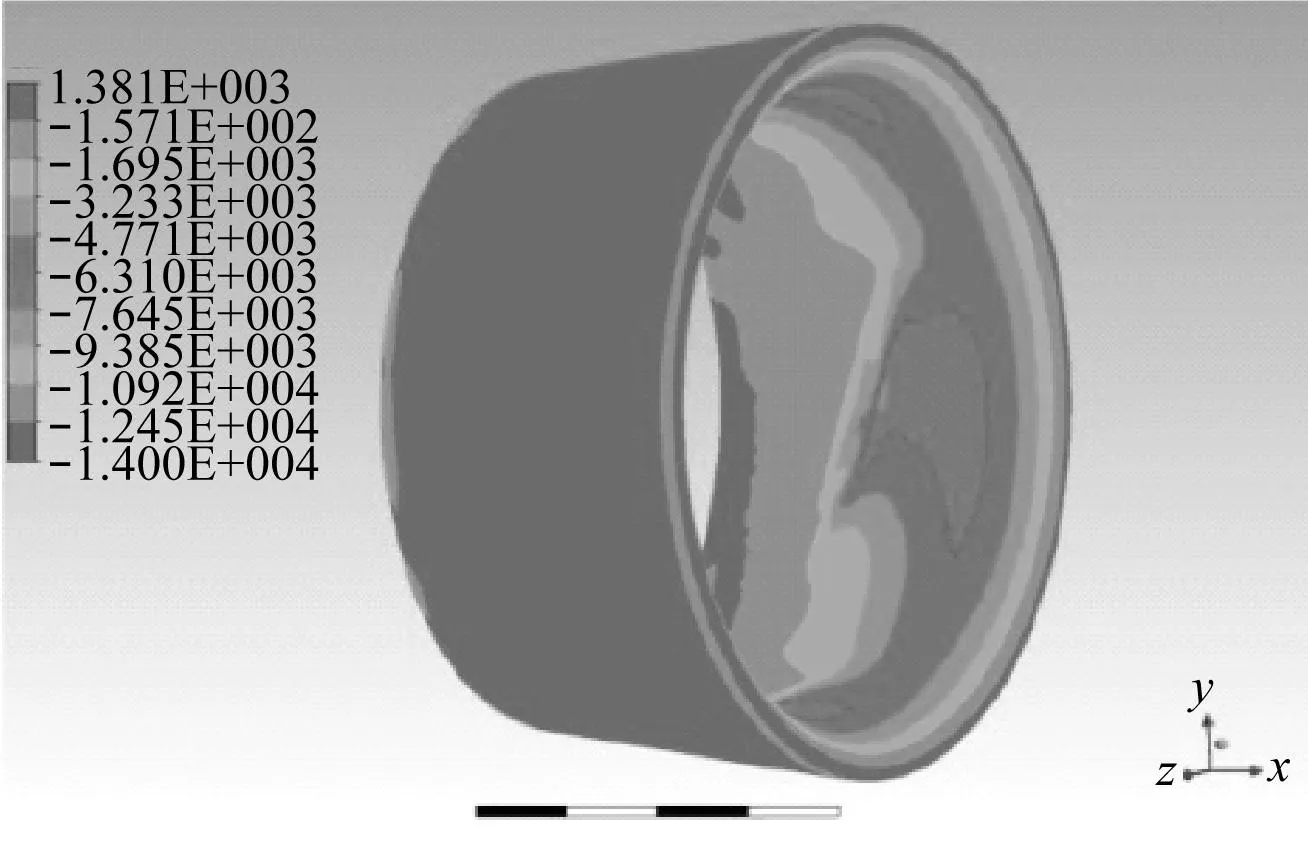
(c) 叶梢间隙为3 mm时导管壁压力分布

3结语

叶梢间隙的变化改变了导管与叶梢之间的诱导速度，从而改变了导管螺旋桨的水动力性能。根据螺旋桨理论，推进器输出的推力主要与水流速度增量(因为流体的反作用力即为推力)有关，即轴向诱导速度。特别是经过螺旋桨盘面处的水流速度增量，这个因素决定了导管螺旋桨的推力。由于叶梢间隙的“缝隙节流”作用，叶梢间隙越小，盘面处的轴向诱速度越大，则推进器所能提供的推力越大。同时，叶梢间隙越小，则由于叶梢引起的效率损失也越小，导管螺旋桨的效率越高。

叶梢间隙为1 mm的导管螺旋桨敞水水动力性能与敞水试验值最为接近。

参考文献：

[1]李坚波. 叶梢间隙对导管桨性能的影响分析[J]. 船海工程, 2010, 39(3): 36-39.

[2]刘登成, 洪方文. 导管间隙对带前置定子导管桨水动力性能的影响研究[C]. 第十五届全国水动力研讨会暨第十二届全国水动力学学术会议文集, 2013.

[3]朱俊飞. 导管螺旋桨水动力分析与优化研究[D]. 武汉:武汉理工大学, 2013.

[4]盛振邦, 刘应中.船舶原理[M].上海：上海交通大学出版社，2004.

[5]王献孚, 周树信, 陈泽梁, 等. 计算船舶流体力学[M]. 上海:上海交通大学出版社, 1992.

[6]张亮, 李云波. 流体力学[M]. 哈尔滨:哈尔滨工程大学出版社, 2006.

[7]欧礼坚, 李德玉, 张薇. 基于CFD的导管桨叶梢与内壁间隙对水动力性能影响分析[J]. 广东造船, 2013(4): 33-35.

[8]赵强. 导管螺旋桨水动力性能和船尾伴流场的CFD模拟[D]. 武汉:武汉理工大学, 2011.

[9]吕晓军, 周其斗, 纪刚, 等. 导管螺旋桨敞水性能的预报和比较[J]. 海军工程大学学报, 2010, 22(1): 24-30.

[10]马艳. 导管螺旋桨的水动力性能分析与设计优化[D]. 哈尔滨:哈尔滨工程大学, 2010.

Influence of Clearance between the Blade Tip and the Inner Wall of Duct on Hydrodynamic Performance of Ducted Propellers

ZhangWencan,DongGuoxiang,ChenWeimin,RenHaikui

(State Key Laboratory of Navigation and Safety Technology，Shanghai Ship & Shipping Research

Institute，Shanghai 200135，China)

Abstract:The viscous flow field of the model of No.19A+Ka4-7010 ducted propeller from MARIN is calculated and analyzed with RANS equations by means of CFD software Fluent, and the hydrodynamic performance curve is obtained. The hydrodynamic performance of the ducted propeller is calculated for Δ=1 mm; 2 mm and 3 mm respectively, where represents the clearances between the blade tip and the inner wall of the duct, to investigate the effect of clearance adjustment. A prototype of the propeller with the clearance of 1 mm is made and tested to check the calculation. The investigation indicates that all the thrust, torque and the propulsion efficiency of the ducted propeller increase as the clearance decreases.

Key words:ducted propeller; blade-duct clearance; CFD (Computational Fluid Dynamics); hydrodynamic performance

中图分类号：U664.33

文献标志码：A

文章编号：1674-5949(2015)04-008-06

作者简介：张文璨(1990—)，男，辽宁沈阳人，硕士生，主要从事船舶推进器水动力性能研究。

收稿日期：2015-05-13