一种新型蚁群随机树的机器人路径规划算法
2016-01-28白金柯吴晓娜
白金柯,吴晓娜
(河南化工职业学院,河南 郑州 450042)
Robot-path Planning Based on Ant Colony Optimization and Rapidly-exploring Random Tree
BAI Jinke,WU Xiaona
(Henan Vocational College of Chemical Technology,Zhengzhou 450042 China)
一种新型蚁群随机树的机器人路径规划算法
白金柯,吴晓娜
(河南化工职业学院,河南 郑州 450042)
Robot-path Planning Based on Ant Colony Optimization and Rapidly-exploring Random Tree
BAI Jinke,WU Xiaona
(Henan Vocational College of Chemical Technology,Zhengzhou 450042 China)
摘要:为提高复杂环境下机器人的路径规划效率,提出了一种用蚁群算法来优化随机树算法的新的全局路径规划算法。该算法有效地结合了蚁群和随机树算法的优点,利用随机树算法的高效性快速收敛到一条可行路径,将该路径转换为蚁群的初始信息素分布,可以减少蚁群算法初期迭代;然后利用蚁群算法的反馈性优化路径,求得最优路径。仿真实验表明,该蚁群随机树算法可以提高机器人路径规划的速度,并且在任何复杂环境下迅速规划出最优路径。
关键词:路径规划;随机树算法;高效完备性;蚁群算法;正反馈性
中图分类号:TP302
文献标识码:A
文章编号:1001-2257(2015)07-0073-04
收稿日期:2015-01-19
基金项目:河南省基础与前沿技术研究计划项目(142300410283);河南省教育厅科学技术研究重点项目(12B520063,14B520065);河南省高等学校青年骨干教师资助计划项目(2013GGJS-230)
作者简介:白金柯(1984-),男,河南巩义人,助教,硕士研究生,研究方向为人工智能、路径规划。

Abstract:In order to improve robotic efficiency of path planning in a complex environment, this paper proposes a global path planning algorithm which makes use of ant colony optimization (ACO) to optimize rapidly-exploring random tree algorithm. The new algorithm effectively combines the strengths of the two algorithms, taking advantage of the high efficiency of the rapidly-exploring random algorithm to quickly converge a possible path, make it into a ACO initial distribution of pheromones, reduce the number of iterations and accelerate the convergence. At the same time, by using the positive feedback technology, the process of finding the optimum path is effectively improved. The simulation experiment shows that the algorithm increases the efficiency of robotic path planning greatly and can plan the best path in a complex environment quickly.
Key words:path planning; rapidly-exploring random tree; efficiency and completeness;ant colony optimization; positive feedback
0引言
路径规划是智能机器人研究领域的重要内容。机器人路径规划的定义是,在含有障碍物的环境中,寻找一条合适的路径使机器人能够从任意起点运动到终点,且在运动过程中机器人应不碰撞到障碍物,路径最优。全局路径规划主要是事先获得环境信息,通过建立合适模型来搜索获得全局最优路径[1]。目前常用的全局路径规划方法主要有:人工势场法、栅格法和各种智能算法等[2-4]。人工势场法算法简单效率高,容易易于实现,且规划的路径较平滑,但是会出现遇到障碍物振荡、局部极值点等问题;栅格法一般可以较快速求得最优解,但是求解质量受栅格大小设置的影响,同时当搜索空间变大时占用的大量的存储空间。近年来提出的智能算法如:蚁群算法、神经网络、遗传算法等在路径规划领域广泛应用,这类算法都有优点,但是都有一定局限性难以适应路径规划的要求[5]。因此需要不断寻找更新的算法,以适应路径规划的更高需求。
蚁群算法(ACO)是一种仿生型智能算法[6-7],主要通过蚂蚁群体内部的信息传递从而实现路径优化的目的,具有信息反馈、分布计算和启发式搜索等特征。广泛的应用与路径规划问题,但普遍存在初期蚁群信息素匮乏,收敛速度慢的问题。
快速扩展随机树(RRT)是目前广泛应用的基于采样的单查询运动规划方法[8]。该算法能够快速地搜索整个环境,通过对环境中点随机采样,把搜索导向未搜索区域,从而搜素出一条从起点到终点的路径。由于该算法随机性,所以具有概率完备性。在有解的前提下,可保证算法获得可行解。但随机树算法也存在重复性差,规划出的路径非最优路径等问题。
综上,首先用随机树算法规划出全局环境下一个可行路径,作为蚁群算法初始信息素分布,再通过蚁群算法对路径进行优化,有效提高算法收敛速度。大量仿真实验表明该方法效果十分满意。
1蚁群随机树算法的路径规划
基于蚁群随机树路径规划算法的基本思想是结合随机树的快速收敛性和蚁群算法最优的特点,快速找到一条最优路径。虽然随机树收敛速度非常快,但是求得的路径不一定是最优路径,同时,同一问题多次规划可得到多个结果,可重复性差;蚁群算法能得到全局最优路径,但速度慢,效率低。本文先利用随机树算法生成一条路径,然后将这条路径用蚁群算法进行优化,该混合算法不仅提高蚁群算法效率,也增强了随机树算法的精度。通过仿真实验,该算法结果令人满意。
1.1 初始化路径
随机树算法是路径规划中常用的一种算法。每次路径选择是以搜索空间中当前的点作为根节点,随机向四周采样,逐渐增加节点,生成一个随机树。当随机树的节点中包含终点时,在随机树的节点中找到一条包含起点和终点的树节点作为规划路径。
随机树构建方法如图1所示。图中为一个拥有若干节点的随机树,x为T的节点,且Tk∈Cfree。同时定义xinit为初始位置,xgoal为目标位置xgoal∈Cfree。令xrand表示在C空间中随机选取的一个点,且xrand∈Cfree。

图1 RRT的构建过程
由于随机树具有较好的完备性,包含了所有可能的路径,但随机树采用随机采样生成,同一任务多次规划会产生多个的结果,这样机器人执行同一任务的重复性就比较差。同时由于随机树的路径点由随机采样生成,所规划出的路径并不一定是最优路径。
如图2所示。图中的路径为从起点S到终点G的随机树路径规划,实线和虚线分别是随机树算法两次规划的路径PRRT。可以看出随机树算法可以找到可行的路径但是每次规划出不同结果,并不能确定最优路径。因此,采用蚁群算法对路径进行修正,搜索出一条真正有效的全局最优路径。

图2 RRT算法路径规划
1.2 信息素的构建
采用随机树算法进行两次路径规划,将两次规划的路径转化为蚁群算法的最初信息素分布。由于这些路径只是相对最优路径,因此,使蚁群在一定范围内进行搜索,对路径进行优化,最终确定出最优的路径。
首先根据环境信息得到蚁群信息素的初始值τi,j(0),然后将随机树得到的最优路径转换为信息素的初始值Δτi,j,接着对初始信息素的进行二次分布,新的信息素量为τi,j,按照式(1)计算。
τi,j=τi,j(0)+Δτi,j
(1)
这样蚁群有了最初的信息素,蚁群将按照式(1)进行路径选择。
1.3 基于蚁群算法最优路径规划


(2)
蚂蚁k(k为任意蚂蚁)在运动过程中,会根据当前路径上的信息素的量决定其下一步的移动,假设在某时刻t,蚂蚁k要从任意位置点i向j移动,其下一移动位置的定义为:

(3)

假设随时间推移,信息素逐渐地挥发。用ρ表示单位时间内信息素挥发后的剩余度。假定在经过h个时刻后,蚁群完成一轮路径规划。此时,将所有路径上信息素的量按式(4)调整规则进行重新设置。

(4)
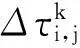
上述蚁群随机树算法主要步骤为:
a.根据环境信息和随机树得到的初始路径得到蚁群初始路径。
b.设置蚁群数目和循环次数。根据式(1)分布路径信息素初始值。
c.启动蚁群,所有蚂蚁根据蚁群移动规则式(2)选择路径点,进行路径规划。
d.重复步骤c,直至到达设定循环时间或者所有蚂蚁到达终点。
e.计算出每只蚂蚁的所走的路径长度L,求解出最优路径。
f.根据式(5)对蚁群在各条路径上的信息素进行更新。
g.若蚁群循环达到规定次数或全部收缩在一条路径上,结束循环。否则转到步聚c,继续循环。
h.输出本次循环最优路径。
2仿真实验
为验证算法的效果,用Matlab软件进行大量仿真实验。蚁群参数的设置为:蚁群数目Na=40,最大循环次数Ma=60,距离信息的重要程度β=2,信息素的重要程度参数α=1,信息素的挥发速度ρ=0.3,常数Q=100。仿真结果如图3、图4所示,其中仿真环境大小为30 m×30 m。图3是本文算法在简单下的搜索的最优路径;图4是在复杂环境下搜索的最优路径。图3的仿真结果给出了一个平滑的路径适合机器人行走。图4的仿真结果表明,只要存在通路,该算法就能迅速规划出较优路径。通过多种环境仿真实验,结果表明,不论环境如何复杂,本算法都能收敛于全局最优路径。
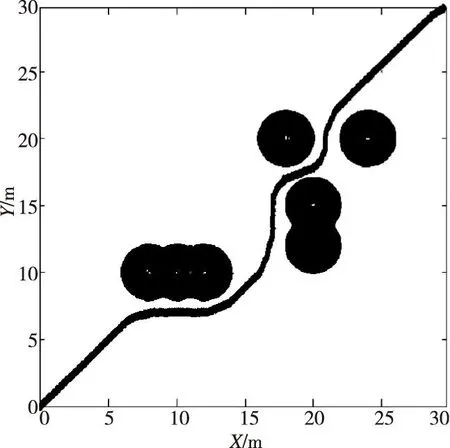
图3 环境1仿真结果

图4 环境2仿真结果
参考文献本文提出的蚁群随机树算法和[7]的蚁群算法,在Matlab中进行90次仿真的比较,结果如表1所示。虽然本文混合算法的复杂性较随机树和蚁群算法高,但由于根据随机树算法的结果作为蚁群算法的初始信息素,大大提高蚁群算法效率和随机树算法的准确度,所以所得结果的有效性和效率均高于蚁群算法和随机树算法。通过多次仿真,该算法在复杂环境下的路径规划,收敛速度快并且收敛路径均全局最优。
表1与蚁群算法的比较

仿真条件蚁群算法本文算法最优路径步数最优解耗时/s最优路径步数最优解耗时/s环境172.12.3155.81.41环境283.42.865.61.6
3结束语
针对机器人全局路径规划问题,提出了蚁群随机树相结合的新算法,该算法大大提高蚁群算法的收敛速度,在规划速度上和效果上均优于蚁群算法。仿真结果表明,该算法在机器人路径规划中的效果好具有实用性。
[1]李磊, 叶涛,谭民,等.移动机器人技术研究现状与未来[J]. 机器人, 2002, 24(5): 475-480.
[2]Cai Wenbin,Zhu Qingbao,Hu Jun.Path planning based on biphasic ant colony algorithm and fuzzy control in dynamic environment [C]//2010 2nd International Conference on Intelligent Human-Machine Systems and Cybernetics.Hangzhou:Ⅱ E Press,2010:333-336.
[3]Keron Y,Borenstein J. Potential field methods and their inherent limitations for mobile robot navigation [C] // Proceedings of the IEEE International Conference on Robotics and Automation.Piscata way, NJ, USA: IEEE, 1991: 1398-1404.
[4]秦元庆, 孙德宝,李宁,等. 基于粒子群算法的移动机器人路径规划[J]. 机器人, 2004, 26(3): 222-225.
[5]吴宪祥, 郭宝龙,王娟.基于粒子群三次样条优化的移动机器人路径规划算法[J]. 机器人, 2009, 31(6): 556-561.
[6]Dorigo M, Caro G D. The modified swarm optimization metaheuristic [M] //Come D, Mdorigo, Glover F, Editors. New Ideas in Optimization. Mc London, UK: Graw Hill, 1999: 11-32.
[7]Bonabeau E, Dorigo M, Theraulaz G. Swarm intelligence: from natural to artificial systems [M].New York: Oxford University Press, 1999.
[8]Lavalle S M, Kuffner J. Rapidly exploring random trees:progress and prospects [C] //Proceedings of the International Workshop on Algorithmic Foundations of Robotics. Hanover, USA, 2000: 45-59.
