基于单面影响系数法的动平衡测量研究

徐　凯，程　念，苗玉彬

(上海交通大学机械与动力工程学院，上海 200240)

A Study on the Measurement of Active Balance Based on Single-plane Influence Coefficient Method

XU Kai, CHENG Nian, MIAO Yubin

(School of Mechanical Engineering，Shanghai Jiao Tong University, Shanghai 200240, China)

基于单面影响系数法的动平衡测量研究

徐凯，程念，苗玉彬

(上海交通大学机械与动力工程学院，上海 200240)

A Study on the Measurement of Active Balance Based on Single-plane Influence Coefficient Method

XU Kai, CHENG Nian, MIAO Yubin

(School of Mechanical Engineering，Shanghai Jiao Tong University, Shanghai 200240, China)

摘要：基于单面影响系数法，提出了一种动平衡测量方法。介绍了单面影响系数法的测量原理、整个测量系统的组成，并采用整周期采样法实现了对振动信号的提取。实验结果表明，该动平衡测量方法能够准确得出系统的动平衡量，对于消除旋转机构中的动平衡量具有一定的应用价值，也为其他场合下的动平衡测量提供了参考。

关键词：旋转机械；动平衡测量；单面影响系数法；整周期采样法

中图分类号：TP29

文献标识码：A

文章编号：1001-2257(2015)07-0007-04

收稿日期：2015-02-09

基金项目：国家重大科学仪器设备开发专项项目(2012YQ15008703)

作者简介：徐凯(1989-)，男，安徽淮南人，硕士研究生，研究方向为工业自动化及振动噪声控制；程念(1992-)，男，湖北武汉人，硕士研究生，研究方向为设备智能检测。

Abstract：The method for active balance measurement based on single-plane influence coefficient method is described. The measurement principle of single-plane influence coefficient method, the composition of the entire measuring system and the signal extraction algorithm based on full-period sampling method is given in detail. Experimental results show that the active balance measurement method can obtain the magnitude and phase of active balance accurately. So this measurement method is of great value in eliminating the active balance in rotational mechanism, and can also serve as a reference when measuring active balance in other situations.

Key words：rotational mechanism；measuring of active balance；single-plane influence coefficient method；full-period sampling

0引言

旋转机械在工业生产中应用广泛，如汽轮机转子、风机和脱粒机中的滚筒以及电机转子等。转子的不平衡是这些机械设备的主要振动源。减小振动可以延长机械的使用寿命、改善其性能和降低噪声，同时也为节约能源创造条件。

消除动平衡需要动平衡的测量和动平衡的校正两个基本过程。其中动平衡的测量是消除动平衡的基础。为此，采用基于单面影响系数法的动平衡测量方法，以高性能DSP F2808芯片作为测控单元，在振动信号提取上采用整周期采样法，实现了数字化的动平衡测量。实验结果表明，采用该测量方法能够快速、准确的得到动平衡量[1]。

1单面影响系数法的测量原理

如图1所示，对于工业机械中的刚性转子，在校正面A、B上有不平衡量(UA、UB)，两轴承A、B处的阻抗为ZA、ZB，转子转速为ω，M为转子质量，Jc为转动惯量，当转子的结构、尺寸等确定后，这些都为常量。不平衡量(UA、UB)对应的稳态响应分别为(XA、XB)，它们之间的关系可以表示为：

(1)

图1　刚性转子动平衡测量示意

由上述方程可以解出：

XA=α1U1+α2U2

(2)

XB=β1U1+β2U2

(3)

α1、α2、β1和β2对于固定转子为常数。

如果不考虑平衡力偶，(2)、(3)式将变为

XA=αU

(4)

XB=βU

(5)

可见，单面影响系数法只需要利用任意一个方程即可。

转子具有的初始不平衡量为U0，系统的影响系数为α。启动转子使其转速达到工作转速ω，利用加速度传感器测得转轴A处的稳态响应为XA0。然后在校正面上加上已知的平衡量U1(|U1|=配重×配重半径)后，再启动转子使其达到工作转速ω，测出此时转轴A处的稳态响应XA1，由式(4)可得：

XA0=αU0

(6)

XA1=α(U0+U1)

(7)

由式(6)和式(7)式可得：

(8)

从而实现了基于单面影响系数法的动平衡测量[2]。

2系统总体结构

动平衡测量系统如图2所示。图中DSP采用TI公司推出的主频100MHz的F2808芯片，其内部有eCAP采集模块和ADC模块等。加速度传感器和光电传感器安装在校正面A上。加速度传感器将不平衡量所产生的振动信号转换为电压信号，该信号经过跟踪滤波、信号放大和AD转换后，得到离散的数字量。而光电传感器得到的脉冲信号经过光电隔离后进入DSPF2808芯片，为加速度传感器提供相位信息。F2808芯片计算出动平衡量后利用RS232总线将数据传输给上位机，通过上位机将动平衡大小和相位显示出来[3]。

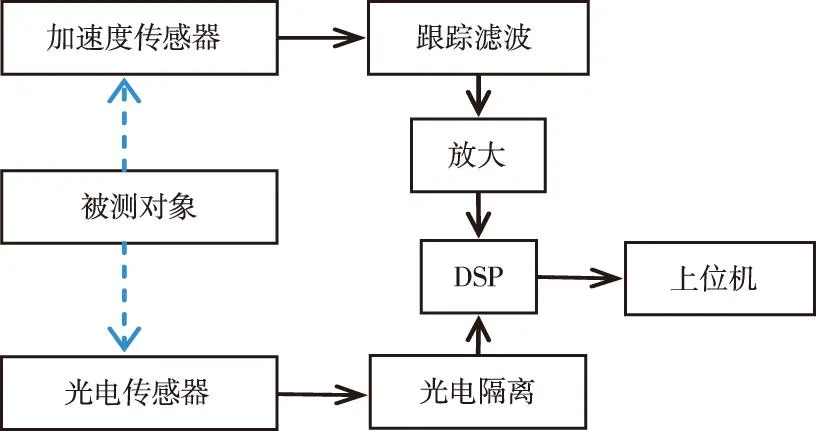
图2　动平衡测量系统

3振动信号的提取

不平衡的振动信号可以表示为式(9)的形式：

e(t)=E0+Esin(ωt+φ)+

(9)

其中，基波分量Esin(ωt+φ)是希望得到的量，它正是不平衡量所引起的振动信号，其角频率与转子转速相同，其幅值和相位与不平衡量的幅值和相位对应。只要计算出幅值E和φ后，根据式(9)即可计算出不平衡量的幅值和相位[4]。

3.1　整周期采样法的实现

实际测量中，由于不平衡量的作用，加速度传感器得到的信号是周期性正弦信号。但信号通常会含有谐波和干扰，从时域上分析无法得出有用信号，于是对信号进行频谱分析就显得尤为必要。F2808采集得到的是经过AD转换的离散、有限的数据点，离散信号在进行频谱分析时候很容易产生频谱泄漏和栅栏效应等不利影响。因此，选择整周期采样法，能够有效减小这些不利因素[5]。

测量时，转子以工作转速V稳定工作，加速度信号为连续模拟量x(t)，经AD转换后得到离散信号x(n)，采样频率为fs，由离散傅里叶变换，可得：

(10)

其逆变换为：

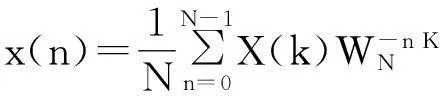
(11)

其傅里叶级数为：

(12)

傅里叶级数系数为：

(13)

实际上，DSP只能对有限时长的信号进行处理。在时域上的表现就是将信号乘以一个时域的有限宽矩形窗函数。采样后信号为：

x′(t)=x(t)ω(t)

(14)

采样时，可以将窗函数宽度设置为信号周期的正整数倍，即保证采样得到的点至少包括一个完整信号周期，则窗函数为：

(15)

其傅里叶变换为：

(16)

根据式(16)与式(12)，得到

(17)

当kfs=nf0时，有：

(18)

k，n为正整数，采样点数为N=iT0/Ts，将其代入式(18)，得：

(19)

由上式，对信号x(t)加宽度为i矩形窗函数，再对其做傅里叶变换。假定N为采样点数，T为采样时间，K为每周期采样点数，则采样频率为：

(20)

经过傅里叶变换之后，信号的频率为：

(21)

离散傅里叶(DFT)的频率谱线是离散的，只有在采样周期为正整数时，才能正好对应DFT的某一谱线，这样就可以准确提取该频率下信号的幅值。

整周期采样法主要有2种实现方式：硬件实现和软件实现。硬件电路一般通过编码盘提供同步信号控制AD模块的采样启动和停止；软件实现方式是通过主控制器内部精确的定时器来控制AD模块的启动和停止。

选择硬件方式实现整周期采样。光电传感器一旦有脉冲信号输出，则DSP启动AD转换，开始采集加速度传感器信号；等到第6个脉冲信号到来DSP停止AD转换，保证采样周期为5个主轴旋转周期，也保证了采样周期是旋转周期的整数倍[6]。

3.2　动平衡信号幅值和相位的提取

主轴的工作转速为240 r/min时，则振动信号的基频信号周期为：

(22)

于是只需要计算4 Hz的幅值即可。以整周期采样方法采集1个采样周期，即5个主轴旋转周期，设定采样频率为fs=200 Hz，则采样点数为：

N=fs×5T0=250

(23)

经过离散傅里叶变化之后，频谱图上的频率分辨率为：

(24)

采集得到的250个点中，与需要的基频信号频率相关的对应点数为：

(25)

根据上述理论，只需计算第5个点处的离散傅立叶变换的值：

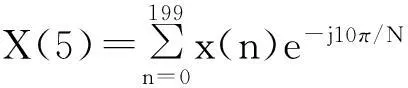
(26)

仔细观察离散傅里叶变换的运算可以得知，其系数具有以下重要规律：

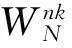
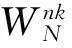
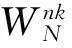
利用上述3个规律，可以大大减小离散傅立叶的运算量。又由于

(27)

故

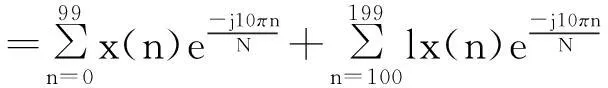
(28)

4试验结果

以摇床的动平衡测量为例，在没有进行动平衡补偿的刚性转子上测量其动平衡量。将转子转速调整为100r/min，则基频信号的周期为：

(29)

图3和图4分别为初始状态下测得的振动信号和进行DFT运算后的频率响应信号；图5和图6分别为加配重后的振动信号和其进行DFT运算后的频率响应信号。

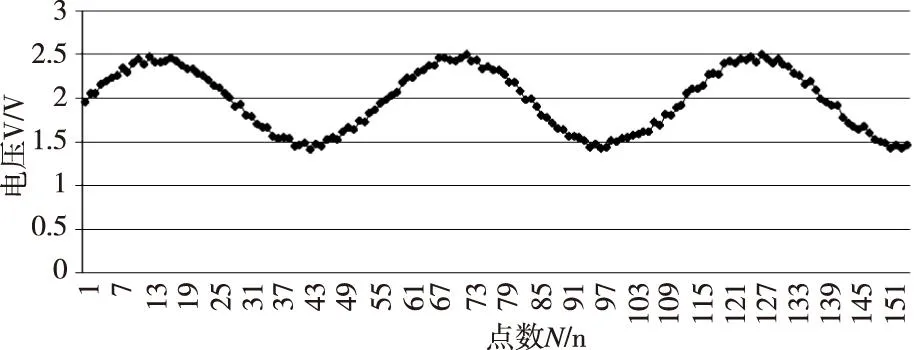
图3　初始状态振动信号时域曲线

图4　初始状态振动信号幅频响应曲线

图5　加配重后振动信号时域曲线

图6　加配重后振动信号幅频响应曲线

图3、图4和图5、图6所示的振动信号的有效值如表1所示。根据添加的配重距离零点位置，由配重产生的已知不平衡量方向为θ1=90°，大小为：

U1=0.1×0.1=0.01 kg·m

经过矢量运算，根据式(8)可得，系统不平衡信号为U0=0.378 kg·m，θ0=32.018 2°。

表1振动信号的有效值

测量环境幅值相位初始状态XA00.8955.0124加配重状态XA10.93205.2312

5结束语

针对工农业生产中旋转机构的动平衡测量，构建了以高性能DSP芯片为核心的测量系统，并采用加速度传感器测量振动信号的大小，采用光电传感器测量振动信号的相位。分析了刚性结构影响系数法测量原理，给出了基于单面影响系数法的测量过程；并针对振动信号的提取特点提出了整周期采样法，减小了采集过程中的运算量。实际试验与应用结果表明，该测量方法能够准确得到动平衡值的大小与相位，对由旋转部件构成的机械设备的生产应用和维修具有实际应用价值，也为其他场合下的动平衡测量提供了参考[7]。

参考文献：

[1]李传江, 费敏锐,张自强. 高精度动平衡测量中不平衡信号提取方法研究[J]. 振动与冲击，2012, 31(14): 124-127.

[2]冯英鹏. 高精度动平衡测量中振动信号处理方法研究与实现[D]. 上海: 上海师范大学，2013.

[3]杨克己. 基于DSP的数字式动平衡测量系统及其关键技术的研究[J]. 仪器仪表学报，2005, 26(8): 458-460.

[4]李英霞,蔡萍,秦鹏，等. 压电传感器在动平衡测量系统中的设计与应用[J]. 自动化仪表，2008, 29(12): 1-4.

[5]Lee Soo-Hun,Kim Bong-Suk,Moonetal Jong-Duck. A study on active balancing for rotating machinery using influence coefficient method [C]//IEEE International Symposium on Computational Intelligence in Robotics and Automation，2005：659-664.

[6]胡庆翰,蔡萍,秦鹏，等.一种新型高精度动平衡测量系统[J]. 传感技术学报, 2007 20(7): 1506-1509.

[7]钱冰. 基于DSP的嵌入式动平衡测试系统的研究[D]. 大连: 大连理工大学, 2005.